涉及Δλ算子的Kirchhoff方程基态解的存在性①

陈佳， 李麟

1.重庆工商大学 数学与统计学院，重庆 400067； 2.经济社会应用统计重庆市重点实验室，重庆 400067

我们知道Kirchhoff方程考虑的是横向振动产生的弦长变化，具有较好的物理意义，同时吸引了大量学者们的关注． 文献[1]在R3中通过变分方法得到当非线性项f满足次临界条件时Kirchhoff方程解的集中行为以及存在性结果． 随后，文献[2]考虑了具有临界增长的非线性项f的Kirchhoff方程的正解的多重性和集中性． 文献[3]运用单调性和全局紧性引理讨论了Kirchhoff方程正基态解的存在性，并且推广了文献[1]中的结果． 文献[4]讨论了非线性项f无紧性条件下Kirchhoff方程的基态解． 文献[5]考虑了具有一般位势的Kirchhoff方程的Nehari-Pohozaev型基态解． 对于Kirchhoff方程基态解的存在性问题已经得到广泛的研究，但对于f满足超线性条件时基态解的结果还很少． 受文献([1-9])的启发，本文主要考虑如下的Kirchhoff方程的基态解：

(1)

其中a，b是正常数，λ=(λ1∂x1u，…，λN∂xNu)，并且Δλ是强退化椭圆算子，具体形式为

关于该算子更多的性质，参见文献[10-13]． 这里非线性项f满足以下条件：

|f(x，t)|≤c0(|t|+|t|p-1) ∀(x，t)∈R3×R3

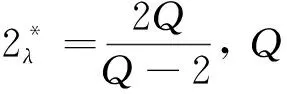
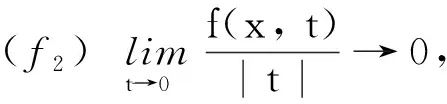
(f3)存在μ>4 使得f(x，t)t≥μF(x，t)，∀(x，t)∈R3×R．

位势V(x)满足如下条件：

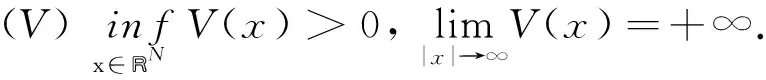
首先，定义空间

E={u： |λu|2+V(x)u2dx<+∞}

显然，E是Hilbert空间，具有内积

和范数

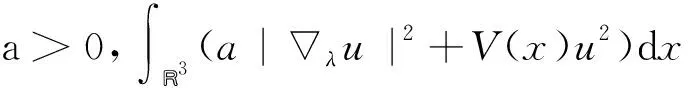
其次，我们在E上定义方程对应的能量泛函

(2)

不难得到J∈C1(E，R)，具有导数

(3)

注1本文主要在R3中讨论Kirchhoff方程基态解的存在性，最大的困难在于全空间 R3中我们无法得到嵌入紧性． 因此，为了找到J的临界点，我们将通过Nehari流形的方法寻找最小能量解，并且该解就是方程的解．

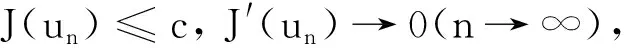
N={u∈E{0}： 〈J′(u)，u〉=0}

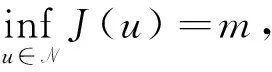
引理1设条件(f1)-(f3)和(V)成立，则任意的(PS)序列{un}是有界的．

(4)

(4)式意味着{un}在E上有界．

引理2设条件(f1)-(f3)和(V)成立，则N≠∅，并且存在常数k>0，使得∀u∈N，J(u)>k．

|F(x，t)|≤εt2+Cεtp∀x∈R3

(5)

由文献[14]的引理2.2有

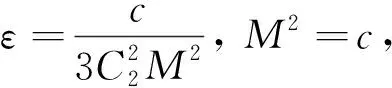
显然这是矛盾的，所以u0≠ 0．又根据文献[6]的引理2.2和条件(f1)，可以得到

(6)

因此

(7)

从而得到

所以〈J′(u0)，v〉=0，u0≠0，得到N≠∅．

下面证明J(u)>k． 因为对每一个u∈N都有〈J′(u)，u〉=0，所以由(5)式可以得到

因此，存在常数γ>0，任取u∈N，使得‖u‖2≥γ．又根据条件(f3)，可以推出

所以存在常数k>0，使得∀u∈N，J(u)>k．

定理1设条件(f1)-(f3)和(V)成立，则方程(1)存在一个基态解．

这就意味着u∈N，有J(u)=m． 所以u∈E是J的基态解．