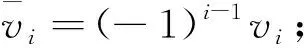一类具有超线性项的Kirchhoff方程的变号解①

张玲， 吕颖

西南大学 数学与统计学院，重庆 400715

本文考虑如下一类Kirchhoff方程最小能量变号解的存在性：

(1)

其中a，b>0，位势函数V具有双位势阱． 该类方程首次是由D’Alembert在研究伸缩绳的自由振动的经典波动方程时提出．Kirchhoff问题具有广泛的研究意义，它在物理问题、人工智能和弹性理论等诸多领域都有十分广泛的应用．在非线性项满足不同条件的假设下，关于Kirchhoff方程正解的存在性和多解性，以及基态解的存在性已有很多结果[1-8]． 但是研究方程(1)的变号解的文章很少[9-11]． 文献[11]设V具有双位势阱，非线性项是渐近三次的，研究了方程(1)最小能量变号解的存在性． 本文假设位势函数V有双位势阱，并且假设f满足超三次条件，研究了最小能量变号解的存在性．在本文中，V和f满足下列条件：

(V1)V∈C(RN，R)，V(x)≥0，并且存在c0>0，使得集合{x∈RN：V(x)

(f1)f(t)∈C(R3×R，R) ，存在常数2

令H是加权索伯列夫空间

在H上的范数为

由条件(V1)，(f1)，(f2)易知I是连续可微的． 若u∈H1(R3)是方程(1)的解且u±≠0，则u叫做方程(1)的变号解，其中u+=max{0，u}，u-=min{0，u}． 若u是方程(1)的一个变号解，且对任意的变号解v都有I(u)≤I(v)，则u叫做方程(1)的最小能量变号解．

定义流形

m=inf{I(u)：u∈M}

下面介绍本文的主要结果：

定理1假设条件(V1)-(V2)和(f1)-(f4)成立，则方程(1)至少有一个最小能量变号解．

注1(i) 条件(V2)说明位势V具有双位势阱；

引理1若条件(V1)，(V2)和(f1)-(f4)成立，则M≠∅．

其中

此等式可以等价为

其中

考虑带参数υ∈[0，1]的方程组

(2)

令

U={υ：υ∈[0，1]，使得方程组(2)在R+×R+中有解}

首先证明0∈U． 由于g0(s，t)与t无关，q0(s，t)与s无关，则不失一般性，只需要证明存在s1>0，使得g0(s1，t)=0成立．

(3)

由条件(f3)和(f4)成立，有

(4)

结合(3)式和(4)式知，当s>0足够大时，有g0(s，t)<0． 由g0(s，t)的解析式知，当s>0足够小时，有g0(s，t)>0． 由g0(s，t)的连续性，则存在s1>0使得g0(s1，t)=0． 因此得证0∈U． 由条件(f4)，有f′(t)t2>3f(t)t，则由隐函数定理可证明U在[0，1]上既是开集也是闭集，类似的证明可参见文献[12]． 故完成了引理1的证明．

引理2若条件(V1)，(V2)和(f1)-(f4)成立，则M是H中的闭集．

证当u∈M时，有〈I′(u)，u±〉=0，由条件(f1)，(f2)和索伯列夫嵌入定理，对∀ε>0，存在Cε>0，使得

所以

‖u±‖≥c

(5)

〈I′(u)，u+〉=〈I′(u)，u-〉=0

因此有u∈M，即M在H中是闭集．

定义函数φ(s，t)=I(su++tu-)．

引理3若条件(V1)-(V2)和(f1)-(f4)成立，假设u∈H，并且u±≠0，则：

(i) 若φ′s(1，1)≤0且φ′t(1，1)≤0，则存在唯一一对正数0

(ii) 若φ′s(1，1)≥0且φ′t(1，1)≥0，则存在唯一一对正数su，tu≥1，使得suu++tuu-∈M．

证

(6)

其中

结合条件(f1)-(f4)可得： 当su>0且足够小时，有φ′s(su，su)>0，φ′t(su，su)>0； 当tu>0且足够大时，有φ′s(tu，tu)<0，φ′t(tu，tu)<0 ． 则存在0

φ′s(r，tu)<0φ′s(R，tu)<0

φ′s(su，r)>0φ′s(su，R)>0

由Miranda定理，存在su，tu，并且r

φ′s(su，tu)=0φ′t(su，tu)=0

故suu++tuu-∈M． 假设su，tu存在但不唯一，结合条件(f4)可推出矛盾，故存在唯一一对su，tu使得suu++tuu-∈M．

不失一般性，假设su≥tu>0，由suu++tuu-∈M，有

(7)

根据φ′s(1，1)≤0，有

(8)

结合(7)式和(8)式，得到

若su>1，由条件(f4)可推出是矛盾的． 因此有su≤1，(i)得证．同理可证明(ii)．

引理4若条件(V1)，(V2)和(f1)-(f4)成立，则极小化序列{un}∈M在H中是有界的．

证令{un}∈M是极小化序列，则有

因此，{un}在H中是有界的．

证对任意u∈M，有

即I在M中有下界，根据Ekeland变分原理知极小化序列{un}⊂M满足

(9)

由h的定义可知h±(0，0，0)=0，且h±(t，s，l)是连续可微的． 令

则有

因为un∈M，故有

由

可得

同理可得

则由隐函数定理可知，存在常数δn和函数sn(t)，ln(t)∈C1((-δn，δn)，R)，使得sn(0)=ln(0)，并且对任意的t∈(-δn，δn)，有

h±(t，sn(t)，ln(t))=0

(10)

即

(11)

下证{s′n(0)}和{l′n(0)} 是有界的． 根据(10)式，有

(12)

其中

根据(12)式，有

(13)

其中

由{un}在H的有界性和简单计算，可得

下证detM1>0．

并且结合(5)式，有

再结合(13)式可得{s′n(0)}是有界的，即对任意φ∈H，有|s′n(0)|

由{un}，{s′n(0)}和{l′n(0)}的有界性，有

|〈I′(un)，φ〉|=o(1)‖φ‖

定理1的证明由引理4和引理5，可知存在极小化序列{un}⊂M，满足

(14)

(15)

其中

注意到

在(15)式中取φ=u±，于是有

〈I′(u)，u±〉≤0

由引理3可知，存在(su，tu)∈(0，1]×(0，1]，使得

由条件(f4)，有