供应链网络均衡下碳税与碳交易政策比较

杨玉香,李剑锋,金芳芳,孟丽君

(中国计量大学经济与管理学院,浙江杭州 310018)

1 引言

当前,环境破坏与污染越来越严重,温室气体的排放严重超标,环境问题愈发严峻,给人类生存与发展带来巨大的危害,这一问题已引起各国政府高度重视.为控制碳排放量,很多国家开始实施低碳政策:碳税、碳限额、碳限额与交易、碳补偿等规制政策,其中碳税政策和碳限额与交易政策(以下简称为碳交易)被广泛采用和实施[1].碳税政策以价格控制为特征[2],权威部门通过单位税或总量税的形式,对企业的碳排放征税.碳交易政策以数量控制为特征,权威部门为企业的碳排放量设置一个限额[3],在碳交易市场内,企业间可以进行交易,即若企业的配额过剩,其可将多余的配额在市场上交易出去,若企业的配额不足,则其可在市场内购买更多的碳配额.2005 年,欧盟碳排放市场正式运行,目前已成为全球最大的碳交易市场.2012 年,澳大利亚开始执行碳税政策[4],并于2015 年过渡到碳排放交易体系.2011 年开始,我国启动了北京、上海和广东等碳排放交易试点,2018 年,我国已启动全国碳排放权交易市场,并实施环境保护税法.

低碳政策下,相关减排指标必然分解落实到企业,改变上下游企业的生产运营决策行为[5],对供应链的绩效产生影响.因而,目前已有较多学者研究低碳政策对供应链决策的影响问题.杨珺等建立系统动力学模型,研究强制排放和碳税政策对由一个供应商和一个销售商组成的供应链的库存和订货问题的影响[6].许士春等对比研究了不同减排政策,发现在污染总量控制方面,若企业选择技术改进,则可交易许可政策的效果最差,且可交易许可政策的实施成本最低[7].Palak 等分析潜在低碳规制机制对供应链中供应商和运输模式选择的影响,仅限于库存管理决策[8].Jin 等[9]建立优化模型探讨三种低碳政策对供应链决策和运输模式选择决策的影响.Hoen 等[10]研究减排规制下不同运输模式的库存、运输、减排成本,探讨规制对不确定需求情形下的运输模式选择的影响问题.Chen 等[11]分析了不确定需求下,碳限额和碳交易机制对零售商最优订购批量和运输模型选择的影响.王一雷等[12]针对一个制造商和一个零售商的供应链,建立契约模型研究联合减排机制并协调供应链利润.以上文献仅限于研究减排政策对库存、运输模式决策的影响问题以及减排机制设计问题.

也有学者研究低碳政策对供应链网络规划问题的影响.Zakeri 等[13]提出解析供应链规划模型,以衡量碳定价和碳排放交易机制下规划层供应链绩效,发现碳交易机制在排放生成、成本和服务水平方面,可带来较好的供应链绩效.Fahimnia 等[14]提出碳税政策下整合经济和碳排放的双目标优化模型,提出修正交叉熵求解算法,研究碳税对财政和减排绩效的潜在影响.Marti 等[15]提出考虑碳政策的整数规划模型,分析碳税、碳限额等不同政策对成本和最优网络结构的影响.Mohammed 等[16]构建不确定环境下多周期、多产品供应链网络优化模型,分析碳限额、碳税、碳交易和碳补偿政策对供应链网络优化结构的影响.Haddadsisakht等[17]构建不确定环境下三阶段随机规划模型,设计闭环供应链网络,模型中考虑了碳税税率和需求的不确定性.Zhen 等[18]考虑了需求不确定性,构建包括规制下最小化总碳排量和总运作成本的双目标随机规划模型优化闭环供应链网络.以上文献建立了考虑碳减排的优化模型,探讨了减排政策对网络结构的影响.

可见,目前文献对碳政策下供应链库存、运输模式选择问题研究较多,也有不少学者对比研究碳政策对供应链网络结构的影响问题,然而,未有文献探讨不同低碳政策对多层、多成员供应链网络内企业决策行为的影响,未构建网络均衡模型对比分析不同政策的减排效果.因此,与以上研究不同,本文考虑了两种常用的碳减排政策:碳税政策和碳交易政策,构建包括多制造商、销售商和需求市场的供应链网络,分别分析两种政策下供应链网络各层成员的决策问题及均衡条件,给出碳税政策和碳交易政策的均衡条件,分别构建碳税政策和碳交易政策下的供应链网络均衡模型,提出欧拉求解算法,基于算例对比分析两种碳减排政策下供应链网络间产品交易量、交易价格、需求、需求价格、碳排放量及网络利润的变化,并给出碳税税率的最优值,以及碳交易政策下碳排放信用的最优分配.

2 不同政策框架下供应链网络竞争均衡分析

2.1 问题描述

本文研究的供应链网络包括I个制造商、J个销售商和K个需求市场,如图1 所示.在此网络内,制造商是最大的碳排放者,因此,模型主要考虑制造商的碳排放,基于碳税和碳排放交易框架,分别建立不同政策下的企业决策模型,研究不同企业间的博弈,给出均衡条件,以及不同碳排放政策的均衡条件.模型涉及的下标、决策变量、参数及函数如表1 所示.

表1 模型涉及的下标、决策变量、参数及函数Table 1 Subscripts,decision variables,parameters and functions in the models

2.2 不同政策框架下各层决策者的竞争行为及均衡条件

2.2.1 碳税下制造商的竞争行为及均衡条件

在碳税政策下,针对制造商产生的大量碳排放,权威机构将以税率t向其征税.制造商在支付生产及交易成本之外,还要支付额外的碳税,因此,可建立如下的制造商i利润最大化的最优化模型

其中内生变量为pij的均衡值.

假设供应链网络中I个制造商间为非合作竞争关系,构成Nash-Cournot 均衡[19],即给定其他制造商的决策,每个制造商的目的就是使其利润最大化,进而确定运往销售商的最优产品量.因此,由上述模型,碳税政策下,均衡时,I个制造商的均衡条件可通过如下变分不等式问题表述,即求解,使之满足

式(3)描述的是,若=0,则对制造商i而言,式(3)中的前三项成本之和大于产品价格;若为正,则产品价格等于制造商i的前三项成本的和.

2.2.2 碳排放交易下制造商的竞争行为及均衡条件

令li为制造商i的碳信用数量,l为所有制造商的所有碳信用组合构成的向量,.为企业i的初始分配组合构成向量,+,l0为所有制造商的所有初始分配构成向量,l0.在碳排放交易政策下,可建立如下的制造商i利润最大化的最优化模型

其中式(5)为排放约束.

同理,根据以上模型,分析考虑碳排放交易政策条件下所有制造商同时最优的条件可转化为如下变分不等式问题,求解,使之满足

其中γ1i为约束(5)相对应Lagrange 乘子,所有的乘子组成I维列向量γ1,γ1=(γ11,γ12,...,γ1I)T.对于式(7)中的第三项,若第三项中的排放约束为零,则影子价格,即边际减排成本为正.若其大于零,则影子价格为零.对于第二项,当单位碳信用的价格大于影子价格时,制造商i的碳信用最终的分配为零;当单位碳信用的价格等于影子价格时,制造商i的碳信用最终的分配为正.对于第一项,当制造商i的边际生产成本和交易成本,加上影子价格与单位产品排放量的积大于销售商j愿意支付的价格,此时制造商i与销售商j间交易产品是不会受益的;当两者相等时,为正.

2.2.3 销售商的竞争行为及均衡条件

销售商j利润最大化的最优化模型

其中为pjk的均衡值,为内生变量.

假设网络内J个销售商间也为非合作竞争关系,形成Nash-Cournot 均衡,因此,由上述模型,均衡状态下,J个销售商的均衡条件可通过如下变分不等式问题表述,即求解,使之满足

其中γ2j为式(9)对应的Lagrange 乘子,所有乘子组成J维列向量γ2,即γ2=(γ21,γ22,...,γ2J)T.对于式(11)中的第三项,是销售商j的市场出清价格.第一项表示若交易量为正,则产品交易价格与边际交易成本等于;若交易量为零,则产品交易价格与边际交易成本大于.第二项表示若销售商与需求市场间的交易量为正,则其边际交易成本和处理成本与市场出清价格之和等于市场k愿意支付的价格.

2.2.4 需求市场的竞争行为及均衡条件

对于需求市场k而言,其空间价格均衡条件可表示为

达到均衡下,K个需求市场均需满足式(12)和式(13),因此,可表述为如下的变分不等式问题,即求解,使之满足

2.2.5 碳税的均衡条件

供应链网络中,制造商是主要的碳排放成员,在碳排放税收政策下,权威部门为所有企业制定统一阈值B,令t表示权威部门规定的单位碳排放税税率,则碳排放税收政策的均衡条件可表述为

上述均衡条件等价于如下变分不等式问题,即求解t∗≥0,满足

式(16)可解释为,如果权威部门的税率等于零,则表明达到均衡状态下的企业总碳排放量小于B;如果税率大于零,说明达到均衡状态下的总碳排放量等于B.

2.2.6 碳排放交易的均衡条件

均衡状态下,如果碳信用价格是正的,那么碳信用市场必然出清;如果碳信用供应过剩,那么碳信用价格必然是零.因此,碳信用市场出清的经济系统条件为

上述均衡条件等价于如下变分不等式问题,即求解p∗∈R+,满足

3 不同政策框架下供应链网络均衡模型的建立

在不同碳排放政策框架下,供应链网络达到均衡状态下,网络内的制造商运往销售商的产品数量应该与销售商的购买量一致,且产品数量、价格和碳减排相关的政策必须满足所在决策框架下各均衡条件,现给出如下定义:

定义1在不同碳排放政策框架下,供应链网络的均衡条件:供应链网络每层企业之间产品的卖出量和买入量是一致的,且产品数量、价格和碳减排政策相关量满足供应链网络每层企业的均衡条件及碳减排政策的均衡条件.

定理1碳税政策下供应链网络在均衡条件下的决策问题与下列变分不等式问题是等价的,求解,使之满足

证明先证必要性,均衡条件式(3)、式(11)、式(14)和碳税均衡条件式(16)相加,即可得到式(19).

式(20)可以转换成下式

式(21)恰好是均衡条件(3)、式(11)、式(14)和式(16)的和. 证毕.

对于变分不等式(21),可将其转化为标准变分不等式,即求解Z∗∈H,使得

变分不等式问题是等价的.

定理1 证明过程与定理1 类似,证明略.

在每种碳排放政策下,供应链网络内制造商间及销售商间均为非合作竞争关系,追求利润最大化,达到均衡状态;需求市场内的消费者通过比较做出选择,进而达到均衡.在市场机制作用下,达到整个网络的均衡.均衡状态下,上一层运往下一层的产品量和价格,恰好等于下一层可接受的数量和价格,因此,碳税政策下,均衡表现为交易量、价格和税率须同时满足均衡条件(3)、式(11)、式(14)和式(16),等价于各条件之和;碳排放交易政策下,均衡表现为交易量、价格和碳信用分配量及其价格须同时满足均衡条件(7)、式(11)、式(14)和式(18),等价于各条件之和.

4 不同碳排放政策均衡结果对比分析

本文应用欧拉方法[20−21]求解变分不等式(19)和式(23),以式(19)为例,算法实现如下:

步骤1初始化:设置迭代次数为M,M ←1,设置序列{αM},使得,当M →∞,αM →0,设置ε>0 及初始值Z0∈H.

步骤2计算:通过下列变分不等式问题求解ZM.

步骤3收敛检验,若|ZM −ZM−1|≤ε,则停止循环,否则,M ←M+1,返回步骤2.

本节在理论模型的基础上,对各项成本函数及相关参数合理赋值,并逐步变化相关模型参数,比较不同碳排放政策下供应链网络间产品交易量、需求、价格、碳排放量、利润等均衡结果的变化情况,具体而言,首先,在碳税政策下,研究不同碳排放阀值下网络均衡结果的变化及最优的碳税税率确定问题;其次,在碳交易政策下,分析单位产品碳排放量对网络均衡结果的影响,给出最优碳信用的分配方案;最后对两种政策进行对比,为权威部门制定政策提供依据.

4.1 碳税框架

考虑如下结构的供应链网络:由2 个制造商M1 和M2,2 个销售商D1 和D2,2 个需求市场E1 和E2构成的网络,相关成本函数如下.制造商生产新产品的成本函数为

由以上均衡结果,可以发现:

1)由图2∼图5 可以发现,当碳排放阈值B≥145 时,产品交易量及交易价格均未发生变化;随着环境要求的提高,即碳排放阈值的进一步降低,供应链网络中各成员企业间的产品交易量逐渐降低,网络间交易价格逐渐提高.

2)由图6∼图7 可知,当阈值B≥145 时,需求价格和需求量均保持不变;随着阈值的进一步降低,需求价格逐渐提高,2 个市场的需求量均逐渐降低.

3)由图8∼图9 可知,当碳排放阈值B≥145 时,由于阈值足够大,此时碳税为0,因而对企业未产生影响,企业的碳排放未发生变化;随着阈值的进一步降低,碳排放税税率逐渐提高,每个企业选择逐渐降低碳排放.此外,在不同阈值下,2 个企业的总碳排放量均未超过阈值的限制,可见,企业的碳排放税达到了预期的效果.

4)由图10∼图12 可知,当阈值B≥145 时,制造商1的利润保持1 887.20,制造商2 的利润保持5 668.60,2 个销售商的利润均保持1 121.70,供应链网络总利润为9 799.20;随着阈值的进一步降低,每个企业的利润逐渐下降.当阈值降到50,制造商1 的利润已降为245.00,制造商2 的利润降为727.22,2 个销售商的利润均变成130.91,网络总利润降为1 234.04.

4.2 碳排放交易框架

令制造商M1 和M2 的初始分配和均为60,为分析制造商i(i=1,2,...,I)生产单位产品的碳排量ei对均衡结果的影响,考虑如下三种情况:高单位产品碳排放量(ei=2.5),记为情形1、中单位产品碳排放量(ei=2),记为情形2 和低单位产品碳排放量(ei=1.5),记为情形3,其它成本函数及参数与4.1 节相同,求解均衡模型(23),程序参数设置与4.1 节相同.均衡结果如表2∼表7 所示.

表2 不同情形下的网络间产品交易量均衡结果的变化Table 2 The changes in equilibrium results of product trading volume between networkes under different cases

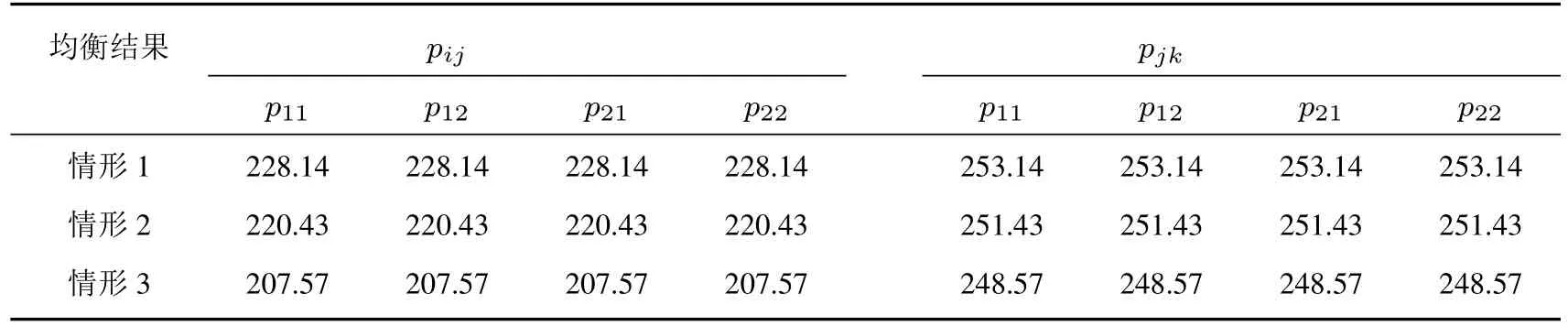
表3 不同情形下的网络间产品交易价格均衡结果的变化Table 3 The changes in equilibrium results of the prices of products traded between networks under different cases

1)由表2∼表4 可知,随着单位产品碳排放量的降低,制造商与销售商、销售商与需求市场间产品交易量均逐步提高,网络间产品交易价格逐步下降,需求市场的需求逐步提高,需求价格逐步下降.

表4 不同情形下均衡结果的变化Table 4 The changes in equilibrium results of demands and demand prices under different cases

2)由表5 和表6 可知,虽然随着单位产品碳排放量的降低,网络间的产品交易量逐步提高,然而,两个企业的碳排放量并未发生变化,因此,所需的碳信用的数量也未发生变化,然而碳信用的价格逐步降低.

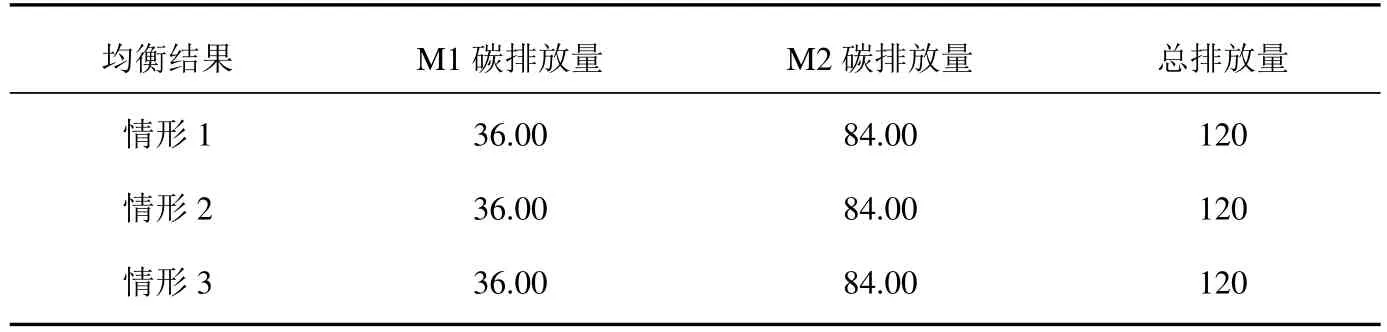
表5 不同情形下碳排放量均衡结果的变化Table 5 The changes in the equilibrium results of carbon emission under different situation

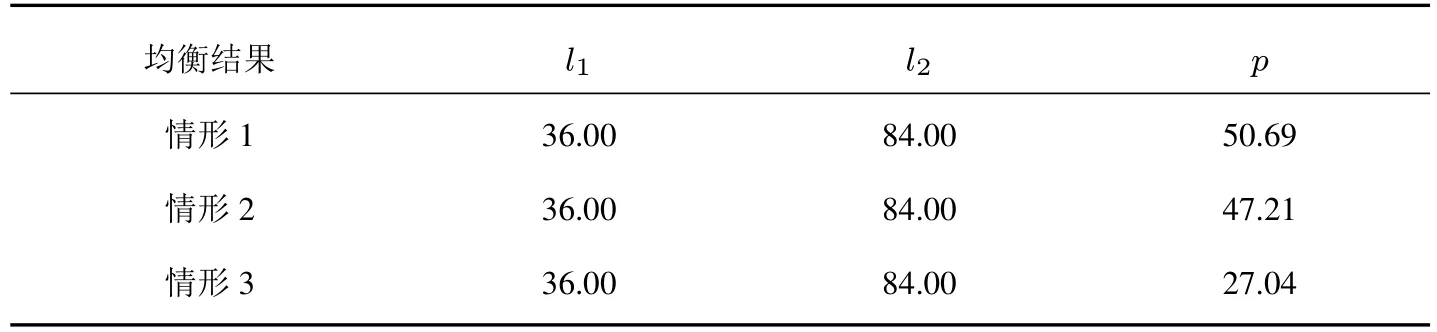
表6 不同情形下碳信用数量及其价格均衡结果的变化Table 6 The changes in equilibrium results of carbon credit quantity and price under different conditions

3)由表7 可知,随着单位产品碳排放量的降低,制造商和销售商的利润均发生了变化,网络总利润逐步提高.

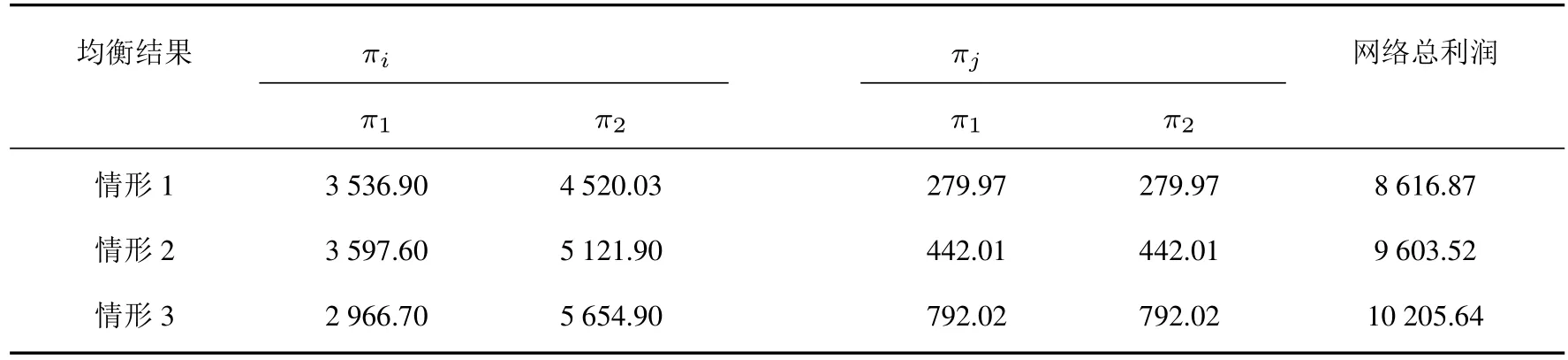
表7 不同情形下网络成员企业利润的变化Table 7 The changes in profits of network member enterprices under different cases

4.3 两种政策的比较

本节比较两种碳减排政策,碳税政策下,将此政策记为P1,设定B=150;碳排放交易政策下,将此政策记为P2,令制造商M1 和M2 的初始分配分别为50 和90,生产单位产品的碳排量ei为1.6,其它成本函数和参数与4.1 节相同.

分别求解均衡模型(19)和模型(23),程序参数设置与4.1 节相同.在碳税政策下,得到最优碳税t∗=2.22;碳排放交易政策下,得到M1 和M2 碳信用的数量分配分别为42.00 和98.00,交易价格为价格12.74.两种政策的减排效果和供应链网络成员企业的利润及网络总利润的对比如表8 所示,可见,碳交易政策下两个制造商的碳排放量均低于碳税政策下的排放量;碳交易政策下,M1 和M2 的利润高于碳税政策下的利润,而D1 和D2 的利润低于碳税政策下的利润,网络总利润高于碳税政策下的总利润.

表8 两种政策下的排放量及利润对比Table 8 Comparison of emissions and profits under two policies

5 结束语

本文考虑两种碳减排政策:碳税政策及碳排放交易政策,针对由多个制造商、销售商和需求市场构成的供应链网络,分别分析了两种碳减排政策下供应链网络各成员企业的均衡条件及行为,以及两种碳减排政策的均衡条件,在此基础上,分别构建两种碳减排政策下的供应链网络均衡模型,给出欧拉方法求解均衡模型,最后,通过算例,首先,在碳税政策框架下,探究不同碳排放阈值下网络均衡结果的变化,给出不同阈值下最优碳税税率;其次,在碳排放交易政策框架下,分析单位产品碳排放量对网络均衡结果的影响,给出不同情形下碳信用的分配方案;最后,对两种碳减排政策进行对比分析.研究发现:碳税政策下,对于企业而言,面对较低的碳排放阈值,企业将选择通过减少产量来达到减少碳排放的目标,由此带来产品价格的上涨,需求也随之下降,导致供应链网络总利润下降;对于政府而言,选择合适的碳排放阈值至关重要,依此模型可决策最优的碳税税率,既能使得供应链网络内成员获得最优的利润,也可达到适当的减排目标.碳排放交易政策下,对于企业而言,可通过采用低碳技术降低单位产品碳排放量,此时可选择提高产品产量,既可达到一定的排放目标,也可提升供应链网络总利润;对于政府部门而言,可依据此模型合理分配碳信用,同时,可制定各种激励措施鼓励企业积极采用低碳技术.对比碳税政策及碳排放交易政策,发现:碳交易政策下的碳排放量低于碳税政策下的排放量,碳交易政策下的网络总利润高于碳税政策下的总利润.可见,碳税政策和碳排放交易政策均可实现减排,然而,碳税政策为供应链中的企业带来了巨大的财务压力,对企业的利润影响较大;碳交易政策下,供应链网络内企业可进行碳信用交易,具有更大的灵活性.此外,碳交易政策下,若要激励供应链上下游企业联合减排,需要制定必要的协调机制,以促使成员企业的利润均能得到合理提升.

本文的模型可用来分析不同政策下供应链网络成员企业的行为变化及政策影响,可为政府制定碳减排政策提供决策参考,也可为企业在碳减排政策的生产及减排策略制定提供一定的依据.