基于进化多目标软子空间聚类的商业银行企业客户信用风险识别

刘 超 谢 菁 李元睿刘宸琦

(1.北京工业大学经济与管理学院,北京 100124;2.北京现代制造业发展研究基地,北京 100124;3.中国人民大学财政金融学院,北京 100872;4.南加利福尼亚大学计算机科学系,美国洛杉矶90001)

1 引言

在产业供给侧结构性改革已取得初步成效的背景下,党的第十三次集体学习会议进一步强调,要深化金融供给侧结构性改革,增强金融服务实体经济的能力.商业银行作为我国重要的金融中介机构,在金融体系中发挥着信用中介职能,促进了资本盈余和短缺之间的融通,提升了金融资源配置的合理性,是我国金融供给侧结构性改革的重要推动者,也是促进金融与实体经济良性循环的活化剂.然而,随着近年来我国经济下行压力凸显,商业银行在扩大信贷供给的同时也面临着日益严重的信用风险.一方面,经济增速放缓、产业结构转型升级导致企业经营状况不断恶化,资产质量下行压力增大[1];另一方面,银行信贷规模增长、客户结构变化以及数据管理变革使得信用评估难度不断加大.在此背景下,商业银行的不良贷款,尤其是企业客户不良贷款显著增加,信用风险持续暴露[2].据银保监会统计,2019 年末商业银行不良贷款余额为2.41 万亿元,不良贷款率为1.86%,连续三年呈现增长态势.同时,各商业银行也报告了近年企业不良贷款率的持续上升趋势,商业银行的经营管理面临着极大挑战.

面对日益攀升的信用风险,如何改进信用风险识别技术、提升信用风险管理水平是当前商业银行风险管理的首要工作.迄今为止,学界和业界已对商业银行信用风险识别技术展开了广泛的研究和讨论,并在一定程度上取得了有益进展.通过汇总既有的研究成果,可以将信用风险识别技术划分为定性法和定量法两大类.其中定量法又可细分为数理统计方法以及机器学习方法.

定性法主要是指专家判别法,其通过信贷专家的知识储备与从业经验对企业客户的信用风险状况进行判断[3].“5C”要素分析法作为应用最为广泛的专家判别法,是通过对借款方的品德、能力、资本、担保品以及条件状况进行充分分析,并予以不同权重,从而进行贷款决策[4].但由于定性法存在着主观性以及偏好性较强等缺点[5],学者们逐渐将研究重点转向了定量分析,数理统计方法由此广泛应用于商业银行企业客户的信用风险识别研究.Milagros 等[6]基于Z 值模型对酒店业企业的信用风险进行了多元回归分析,测算了风险大小.王籽俊等[7]利用Logistic 模型实证了房地产企业的经营状况在很大程度上会影响商业银行信贷资产的质量,从而引发银行信用风险.满向昱等[8]基于企业的信用风险特征,采用Lasso-Logistic 模型对中小微企业信用风险进行了估计和预测,证实了所提模型的有效性.霍源源等[9]构建了一个基于Probit 模型的制造业企业信用风险识别方法,实证了该模型能够较好地预测企业违约事件发生概率.

随着近年金融创新的蓬勃发展,金融衍生品大量涌现,数理统计方法难以驾驭由此产生的海量客户信息以及非结构化数据.在此背景下,基于监督式和非监督式机器学习(Machine Learning)技术的商业银行信用风险识别模型应运而生.在监督式机器学习的应用方面,Raei 等[10]基于神经网络模型构建了一个两阶段混合算法用于估计商业银行企业客户违约概率,并得到了有效的建模结果.Hamori 等[11]在企业信贷违约研究中比较了Bagging,Boosting 等机器学习技术,指出Boositng 的建模效果较优.戴昕琦[12]实证了随机森林模型在商业银行供应链金融信用风险评估方面的有效性.肖斌卿等[13]通过对12 种商业银行内部信用评级模型进行比较,指出基于Levenbery-Marquardt 学习算法的神经网络模型在小微企业信用风险识别中表现最为突出.在非监督式机器学习的应用方面,Andr´es 等[14]以聚类紧凑性作为有效性指标,实证了聚类在识别精度以及贷款决策利润方面都优于其它模型.Bai 等[15]提出了一个新的分离性聚类有效性指标,实证了改进的聚类算法在建模效果方面具有有效性.熊正德等[16]以沪深A股制造业上市公司为研究对象,指出加权模糊C 均值聚类能够显著提高信用违约识别的准确性.

综上所述,既有研究已构建了形式多样的商业银行企业客户信用风险识别模型,具有一定的实践意义.但仍存在着两点不足:一是既有研究并未将新的用户画像以及业务交易场景下信用数据集呈现出的高维、类不平衡等特征纳入信用风险识别模型的构建过程,难免导致模型在风险识别准确性和稳健性方面产生偏差,同时也影响了模型的泛化能力.二是既有研究侧重于风险识别模型的构建以及实证结果的有效性分析,忽视了企业信用风险的关键影响因素,从而难以深入探究企业客户的内在特征,无法为商业银行信用风险的有效管理和防范提供决策支持.

针对以上不足,本文在考虑信用数据集自身特征以及企业信用风险影响因素的基础上,将一个进化多目标软子空间聚类(EMOSSC)算法应用于现实的商业银行企业客户信用风险识别问题.与其它模型不同的是,该算法既能够识别高维信用数据集潜在的特征子空间,又能够有效处理数据的类不平衡问题.此外,该算法还给出了数据集各个特征维度的权重,并根据权重的大小进行了指标重要性评价.本文将EMOSSC 算法应用于我国商业银行企业客户信用风险识别研究,以期在信贷审批过程中为商业银行的信用风险管理提供政策建议,为商业银行助力金融供给侧结构性改革、提升金融服务实体经济的能力提供有力支撑.

2 进化多目标软子空间聚类

2.1 聚类有效性评价

聚类分析作为一种无监督式方法,可以在缺乏类标签和先验知识的情况下对数据进行分类,以最大化同一类内的相似性和不同类间的相异性[17].然而,数据规模和维度的不断增加导致传统聚类算法难以准确定义度量函数.子空间聚类作为一种将传统的聚类分析与特征选择相结合的技术能够有效解决上述问题,其通过把数据集的原始高维特征空间划分为不同的特征子集,以实现从不同的子空间角度考察各个类的划分意义.

软子空间聚类作为子空间聚类的一个重要类别,是指在高维空间聚类时对每个类的各个特征都分配一个权重,从而测量各个特征对特定类的重要性.软子空间聚类的质量通常取决于聚类有效性指标的选取.Harvin 等[20]提出了加权局部自适应聚类(WLAC)算法,该算法作为一种熵加权软子空间聚类算法,能够有效处理类的不平衡性质以提高聚类的性能.WLAC 算法的有效性指标可以表示为

在式(1)中,WLAC 算法的有效性指标由三项组成:第一项反映了类内紧凑性,第二项与第三项作为惩罚项分别控制了熵和不同类的影响.其中类不平衡问题主要是通过系数zi进行处理.一般情况下,类ci越大,zi越小,这意味着若一个类具有较大的规模或者较大的方差,那么不同类之间的距离将会缩小,反之则扩大.Xik估计了类内紧凑性的平均值,充分考虑类大小的影响.

然而,信用风险识别问题通常具有高维度、类不平衡性质.尽管WLAC 算法将类内紧凑性和信息熵引入聚类有效性指标,但其忽视了类间信息的使用,未对类间分离性进行度量.若一个数据集的不同类之间存在着大小、形状和密度方面的较大差异,那么各个类中的样本点对紧凑性度量的贡献是不同的,这种情况下所有样本点到聚类中心的距离之和并不能有效反映类的紧凑性.因此,为了使聚类有效性指标能够更好地反映并衡量数据集的内部结构,EMOSSC 算法同时考虑了类内紧凑性、类不平衡性和类间分离性,

式(2)共包含四项,第一项衡量了加权类内紧凑性,第二和第三项分别用于控制W和Z的权重,称作W和Z的惩罚项,在一定程度上反映了类不平衡信息,而最后一项用于表示不同类之间的分离.考虑分离性度量项的原因在于,当使用所有聚类中心间的最小距离表示聚类划分的分离性程度时,如果能够实现所有类之间的距离都尽可能的大,那么所有类之间的分离性也将尽可能的大.结合信用数据集内部结构特性,一个好的聚类有效性指标不仅要使得同类的内部紧凑性与不同类之间的分离性尽可能大,还需要充分考虑类的大小的影响,克服类不平衡的缺点.因此,式(2)将每个类的权重和特征权重合并为平均类内紧凑性,且同时考虑了类间分离性,从而试图捕获具有高维特征空间和类不平衡性质数据集的内部结构.

2.2 算法框架

EMOSSC 算法是在考虑了数据自身特征的基础上,将软子空间聚类与进化多目标算法相结合所提出的一个新的商业银行客户信用风险识别算法.首先,将聚类有效性指标(2)转化为一个四目标优化问题(见式(3)),将其作为EMOSSC 的目标函数,并将输入聚类数据集的各个维度规范化为[0,1].其次,基于自适应排序的进化算法(ASEA)[19]解决四目标优化问题.而后,引入一个局部搜索策略以加速算法的收敛.最终,当满足终止条件时,采用期望边际效用(EMU)对最终结进行选择[20].EMOSSC 算法具体步骤如下:

步骤1输入种群规模N,最大迭代次数Gmax,四目标优化问题F,归一化后的聚类数据集T;

步骤2P0,Λ ←ASEA 的种群初始化(N);

步骤3判断G≤Gmax是否成立,若成立,执行步骤4∼步骤6,否则执行步骤7;

步骤4QG ←ASEA 的交叉和变异算子(PG);

步骤5QG ←局部搜索(QG);

步骤6PG+1←ASEA的环境选择算子(PG ∪QG,F,T);

步骤7最终解←EMU(PGmax).

2.3 目标函数

进化多目标算法可以将单目标问题转化为多目标问题,从而有效解决加权系数不宜确定以及系数对初始值高度敏感的缺陷.因此,引入多目标优化策略之后的四目标优化问题表达式为

其中f1衡量了聚类内部的距离之和,f1越小说明类越紧凑;目标函数f2与f3引入权重熵的概念,通过维度权重的负熵和类的权重熵以使目标函数适用于数据分布复杂的问题;目标函数f4衡量了不同类之间的距离之和,f4越小则类间分离性越好.

如式(3)所示,四个目标函数相互平衡制约,当缩小或者扩大子空间规模时,这些目标函数能够很好地应对相应的变动.同时优化四目标函数可以有效地避免传统算法中需预先设定加权系数以及对初始值较为敏感的缺点.

2.4 编码方式

EMOSSC 采用基于类中心的编码方式,每个以类中心坐标的实数表示的染色体包含C ×D个维度,C和D分别表示类别数和特征数,染色体的编码范围在0-1 之间.由于基于类中心的编码方式的聚类中心数C与特征数量D远小于样本点的数量n,因此具有染色体较短的优点.此外,由于每个染色体所包含的基因的位置不是随意排列,而是按照每个基因第一维数据的大小进行升序排列的,因此在这些染色体上应用不同的遗传算子(例如交叉和变异)所需时间更少,这又能够进一步加速算法的收敛[21].

2.5 局部搜索

通过引入一个局部搜索策略,可以实现优化过程的加速以及隶属度矩阵U,聚类权重Z以及特征权重W的更新.对于个体x而言,聚类中心可以定义为

其中隶属度矩阵U可以更新为

聚类权重矩阵Z可以更新为

2.6 最终解选择

多目标优化问题的最后一步是找到一种方法从一组非支配解中选择最终解[22,23].通常是将目标空间中的膝盖点,即具有最大的边际报酬率的点作为最终解.EMOSSC 采用基于效用的预期边际效用(EMU)确定膝盖点[20].

假设已知决策者具有特定函数U(x,λ′),则可计算种群中每个个体xi的决策者效用为U(xi,λ′),从而决策者可以选择效用最高的个体作为最终解.但是,当特定个体失效时,决策者将不得不选择次优个体,此时边际效用的附加成本函数可以表示为

为了计算预期边际效用,此处的效用度量假定效用函数在参数λ中服从均匀分布.以两个目标为例,预期边际效用可以通过对所有可能的线性效用函数进行如下计算:如果所有解都按照f1标准进行排序,则在i处的解由xi表示.此外,目标权值λi,j能够使得解xi和xj具有同样的效用,即

解xi的期望边际效用可以计算为

因此,当出现两个目标函数时,效用测度为U(x,λ)=λf1(x)+(1−λ)f2(x)且λ ∈[0,1],以此类推至两个以上目标函数.通常将总体边际效用最大的个体作为最终解.

3 实证研究

3.1 样本及指标选取

为验证EMOSSC 模型在商业银行企业客户信用风险识别问题中的效果,从沪、深两市A 股市场中选取154 家上市企业作为研究样本,令2018 年首次ST 企业(记为“1”)作为高信用风险样本,共计54 家.同时根据“行业相似、规模相近”的原则[24,25]选择对应的非ST 企业(记为“2”)作为低信用风险样本,共计100 家.选择ST 和非ST 企业作为研究样本的原因在于,被实施风险警示的上市企业通常在财务和经营方面存在异常情况,因此具有较高的信用风险,故可将其作为存在违约行为的一种标志.相反,非ST 公司则可视作信用良好的样本.综合沪、深交易所关于上市公司风险警示的定义,本文选择2017 年财务报表中的数据作为信用风险识别的样本数据.

一般而言,影响企业客户信用风险的因素可以分为财务因素和非财务因素[25].财务因素一般是指定量的财务指标,非财务因素不仅涉及定量指标也涉及定性指标.商业银行通过对借款企业的财务因素和非财务因素进行分析和监控,可以获取信用风险识别和管理的依据[26].基于指标体系构建原则,结合国外权威指标以及我国商业银行现有指标体系,本文分别从财务因素(盈利能力、偿债能力、风险水平、营运能力、现金流量、成长能力)和非财务因素(公司治理、股权结构、外部审计)两方面选取了9 个一级指标、46 个二级指标作为实证研究的备选指标,以此全面反映商业银行企业客户的整体信用状况.信用风险识别指标体系如表1所示.

表1 信用风险识别指标体系Table 1 Index system of credit risk identification

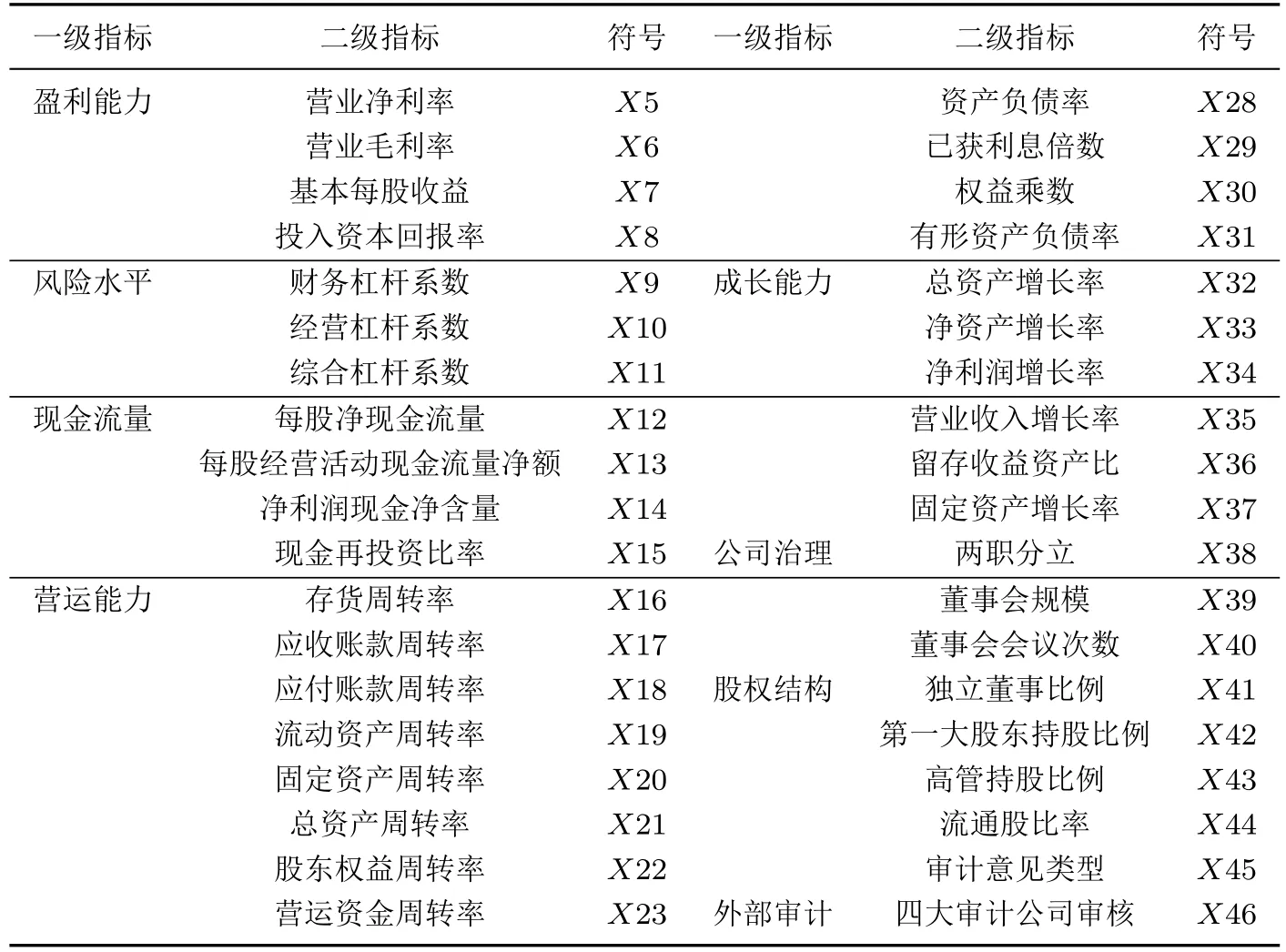
续表1Table 1 Continues

3.2 对比算法及参数设置

本文选取了两个广泛使用的传统聚类算法——K 均值聚类(k-means)[27]和模糊C 均值聚类(FCM)[28],以及三个具代表性的软子空间聚类算法——模糊子空间聚类(FSC)[29]、加权局部自适应聚类(WLAC)[30]、基于进化多目标算法的软子空间聚类(MOEASSC)[31]用作对比算法.

对比算法的参数根据来源论文所确定的范围进行随机选择.根据Yu 等[32]的建议,本文将模糊指数设置为m=min(N,D −1)/[min(N,D −1)−2],其中N和D分别为样本的数量和维度.在FSC 算法中,ε表示加权系数,τ表示模糊参数.根据文献[30],可设置WLAC 中的参数h1和h2.MOEASSC 所采用的基准优化算法NSGA-II 的参数设置与Hu 等[31]相同,而EMOSSC 的基准优化算法ASEA 的参数设置来自于Liu等[19]的建议,Gmax表示最大迭代次数,Np表示种群规模.每个算法在每个测试数据集上运行20 次.参数设置如表2 所示.

表2 参数设置Table 2 Parameter settings

3.3 聚类有效性评价指标与统计检验

本文采用兰德指数(RI)[33],F 度量(FM)[34],第一类误判率(Type-I error)和第二类误判率(Type-II error)[35]这四种常用的聚类有效性评价指标用以评估聚类结果的好坏.

兰德指数主要用于评估类间的相似性;F 度量是一个平衡度量指标,主要是利用信息检索中的精度(precision)以及召回(recall)来衡量一个聚类仅包含特定类的样本占该类的所有样本的程度.第一类误判率(Type-I error)和第二类误判率(Type-II error)解释了正类和负类的错误分类成本.当信用不良申请人被视为信用良好申请人时,会产生第一类误判率.在此情况下,错误分类的申请人将造成违约.反之则会产生第二类误判率.第一类误判率和第二类误判率值越小,聚类结果越好,在信用风险识别问题中,与第一类误判率相关的错误分类成本比第二类误判率更重要[36].

本文使用Wilcoxon 符号统计测试算法性能的统计显著性,其原假设H0为算法A 的平均准确性/平均第一类误判率/平均第二类误判率=算法B 的平均准确性/平均第一类误判率/平均第二类误判率,并用性能等级P表示算法优劣.P可以由以下公式进行计算

其中i和j是算法的序号,如果Aj优于Ai,那么βi,j=1;否则βi,j=0.在给定数据集和性能度量的前提下,具有较小P值的算法具有更好的性能.

4 实证结果

4.1 模型准确性检验

将EMOSSC 算法的聚类结果与其它两个传统聚类算法、三个最先进的软子空间聚类算法进行对比,如表3 所示.由实验结果可以得出如下分析.

表3 算法度量的平均值和标准差Table 3 Mean and standard deviation values of metrics of algorithms

首先,本文提出的EMOSSC 算法在所选样本数据中表现出了最高的准确性,其RI 值和FM 值分别为0.875 1和0.883 9,分别高于第二位的FSC 算法10.9%和6.69%.值得注意的是,尽管EMOSSC 算法的第二类误判率性能略差于WLAC,FSC 和k-means 算法,但是EMOSSC 在第一类误判率方面显著优于其它算法,其主要原因在于本文所选取的商业银行企业客户样本为类不平衡数据集,ST 公司与非ST 公司比例约为1:2,而WLAC,MOEASSC 等软子空间聚类算法无法正确处理类不平衡问题,难以较好地区分少数类,因此才会出现第二类误判率较低而第一类误判率极高的现象(例如,WLAC 的第二类误判率值为0.004 0,但第一类误判率值高达0.837 0).而在信用风险识别问题中,第一类误判率显然比第二类误判率更加重要,错误分类成本的失衡也会进一步导致RI 值和FM 值的偏差.

第二,软子空间聚类算法在高维数据集上的表现总体优于传统聚类算法.尽管FSC,WLAC 和MOEASSC 这三个软子空间聚类算法的准确率总体上与传统的k-means 和FCM 算法相当,但是由于FSC,WLAC 和MOEASSC 的聚类结果高度依赖于预定义的加权系数,因此在没有最优加权系数的先验知识的情况下,无法获得这些算法的最优结果.此外,由于同时对四个目标函数进行优化,且无需预定义加权系数,因此本文提出的EMOSSC 算法表现出了更好的准确性.

第三,对于类别不平衡的企业客户数据集,EMOSSC 能够获得比其它算法更好的结果(WLAC 的结果如前文所述有偏差).此外,FSC 在RI 值、FM 值和第一类误判率中也获得了较有竞争力的表现,这充分说明了权重对于聚类的重要性,以及对类不平衡数据集的平均类内紧凑性进行衡量的必要性.

此外,由表3 可知,在RI,FM 以及第一类误判率中,EMOSSC 算法运行20 次后的标准偏差低于传统聚类算法以及其它三个软子空间聚类算法;而对于第二类误判率而言,EMOSSC 的标准偏差略高于k-means算法,又低于FCM 和其它三个软子空间聚类算法.综上所述,EMOSSC 总体稳定性优于对比算法.

4.2 模型显著性检验

为了避免判别结果的偶然性.本文通过Wilcoxon 秩和检验验证上述实验结果的显著性,图1 表示了6个聚类算法在4 个有效性评价指标中的性能等级,数值越大意味着性能越好.

由图1 可知,本文所提出的EMOSSC 算法在RI,FM 以及第一类误判率中都表现出了最好的性能,位列第一位,而样本的类不平衡性质导致了EMOSSC 在第二类误判率中位列第四位.从整体而言,EMOSSC 算法的显著性最高,紧跟其后的是FSC 算法以及k-means 算法,从而进一步证明了本文所提算法在商业银行企业客户信用风险识别问题中的有效性.

4.3 模型稳健性检验

为进一步验证所提算法在不同数据集上的有效性和稳健性,本文采取相同的规则选取了2017 年的48家ST 公司和96 家非ST 公司作为算法的稳健性检验样本.EMOSSC 及其它5 个对比算法在2017 年商业银行企业客户样本中的评价指标均值和标准差值如表4 所示.

由表4 可知,EMOSSC 的RI 均值和FM 均值显著高于对比算法,第一类误判率均值显著低于对比算法,并且均值的标准差值都更小,说明EMOSSC 在2017 年商业银行企业客户信用风险识别中具有较高的准确性和稳健性.

表4 算法度量的平均值和标准差Table 4 Mean and standard deviation values of metrics of algorithms

与2018 年企业客户样本的实验结果相比,EMOSSC 算法在2017 年样本中的RI 值和FM 值有所下降,第一类误判率有所上升,在一定程度上表明算法的信用风险识别准确性有所下降、分类错误成本有所提升,这可能是由于样本数据差异而导致的.总体而言,EMOSSC 算法在信用风险识别的表现出了较高的准确性和较强的稳定性.

4.4 指标重要性评价

多目标软子空间聚类算法的优势之一在于其能够在高维空间聚类时对每个类的各个特征分配权重,从而测量各个特征对特定类的重要性.因此,在商业银行企业客户信用风险识别问题中,可以根据指标权重的大小来判断指标的重要性,即权重越大的指标对于信用风险识别的能力越强.表5 展示了排名为前15 位的企业客户信用风险识别指标.

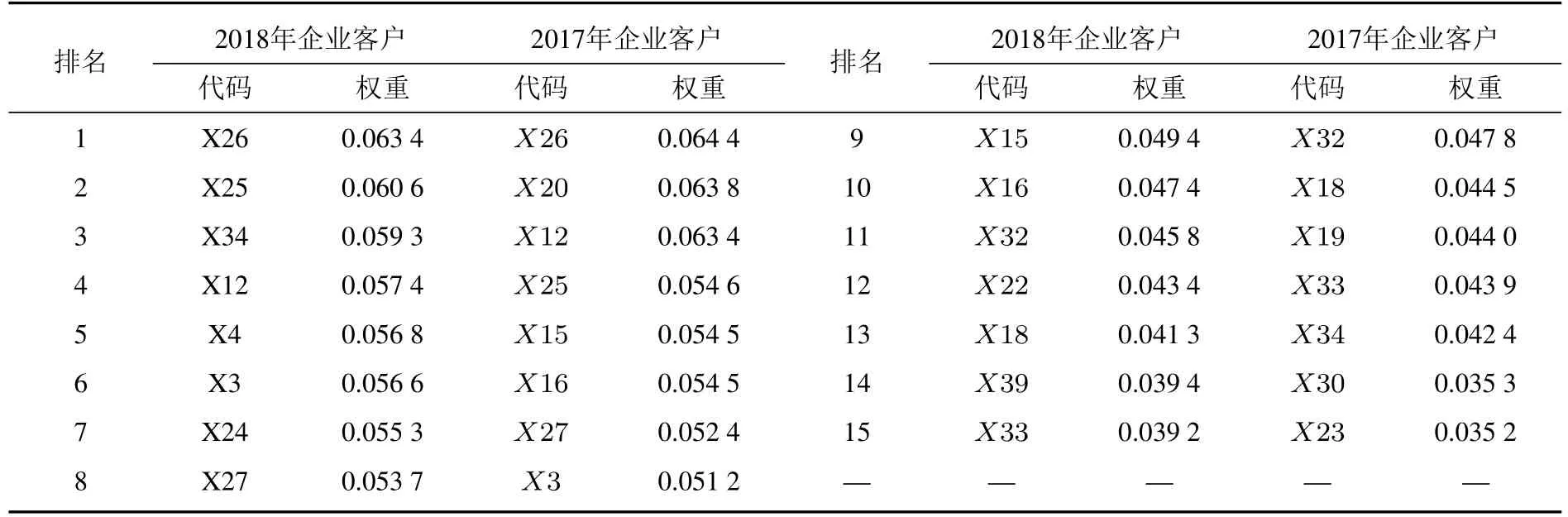
表5 企业客户信用数据集中的指标权重排名Table 5 Ranking of indicators for enterprise datasets

由表5 可知,X3(净资产收益率)、X12(利息保障倍数)、X15(权益乘数)、X16(产权比率)、X18(存货周转率)、X25(财务杠杆)、X26(经营杠杆)、X27(综合杠杆)、X30(净利润增长率)、X32(每股净资产收益率)、X33(留存收益资产比)和X34(净利润现金净含量)这12 个指标对于企业客户信用风险具有较为显著的识别能力,尤其以权重高于0.05 的净资产收益率、利息保障倍数、财务杠杆、经营杠杆和综合杠杆最为突出.因此,在企业客户信用风险识别过程中应该积极关注企业的财务报表信息,如偿债能力、营运能力、成长能力和现金流量等,尤其要侧重于盈利能力和风险水平分析.

5 结束语

本文以商业银行企业客户为研究对象,从信用数据高维、类不平衡的特征出发,将进化多目标软子空间聚类(EMOSSC)算法应用于商业银行客户信用风险识别.研究结论表明,EMOSSC 算法不仅在商业银行企业客户信用风险识别问题中具有良好的适用性,而且能够有效揭示信用风险的关键影响因素,为商业银行信用风险的防范和监管提供指导.未来可以尝试将EMOSSC 算法拓展到同样具有高维、类不平衡性质的其它实际问题中,如生物信息学中的基因选择、医学中的病例筛查、计算机科学中的软件缺陷以及多标签文本分类等,为这些领域的进一步研究提供方法支撑.