基于MRS 的股指期货最优分位数套期保值研究

于孝建梁柏淇徐维军

(1.华南理工大学经济与金融学院,广东广州 510006;2.华南理工大学金融工程研究中心,广东广州 510006;3.华南理工大学工商管理学院,广东广州 510640)

1 引言

股指期货作为一种基础性的风险管理工具,通过对冲股票头寸,可以降低股票组合价值波动的不确定性,使投资者规避股市下行风险.如何计算期货与现货之间的最优套期保值比率,一直是学术界和金融界关注的重点.近年来,中国股指期货交易规则多次松绑,投资者可以以更低的资金成本管理头寸风险,这促进了套期保值需求的满足和市场运行效率的提高.同时,随着期货市场逐步对外开放,外部环境的不确定性也加剧了市场波动风险.为适应中国股指期货常态化交易进程、实现精准化套期保值,需要分析各类市场情况适用的套保比率.因此,本文研究重点在于,当市场波动状态不同以及现货收益率所处分布的分位点不同,套期保值比率会如何变化.

为研究最优套期保值比率,早在20 世纪60 年代,Johnson[1]基于投资组合方差最小化原则提出最小方差(minimum-variance,MV)套期保值比率.MV 目标函数的估计不受统计分布假设的约束,可为多种估计套保比率的方法提供基础,如最小二乘法(OLS)、协整和误差修正法(ECM)和条件异方差方法(ARCH、GARCH).实际应用中,学者们比较了不同方法之间的优劣.如Lien 等[2]、Cotter 等[3]和Copeland 等[4]研究多个股指期货市场发现,由于GARCH 模型方差预测变化较大,其套保比率存在高波动性的不足,因而OLS 套保比率显著优于GARCH 套保比率.Ghosh[5]通过似然比检验和样本外预测证明,考虑协整关系的ECM 套保比率优于OLS 模型.王骏等[6]、佟孟华[7]和Armeanu 等[8]的研究也得到了相似的结论.

上述套期保值比率的计算多使用均值回归分析法,主要关注现货收益与期货收益间的平均关系,仅考虑了收益率分布的集中趋势,忽视了期货和现货收益率在不同分位上的关系,导致在其他分位的对冲效率较低.为此,林旭东等[9]运用分位数回归方法,研究沪深300 期现合约仿真交易的OLS 套保比率,发现套保比率随着分位数的增加先是逐渐增大后逐渐减小.Lee 等[10]将分位数协整回归应用到石油现货市场和期货市场的协整性、因果关系和市场效率研究.放松林旭东等[9]、Lee 等[10]分位数模型截距项在各分位不变的假设后,Lien 等[11]估计20 种期货在15 个分位点的套保比率,发现分位数套保比率取决于现货收益分布,在现货分布两端较小,呈倒U 型,且U 型程度因不同商品和不同频率数据而异.Shrestha 等[12]进一步将分位数回归拓展至能源市场,并计算分位数套保效率1Föllmer 等[13]提出在一定成本约束下获得最大化成功对冲概率的分位数套期保值方法,该方法可看作最小化在险价值(VaR)的动态版本,即最小化套保组合的分位数风险,这与文中提及的分位数套期保值有很大差异.Föllmer 等[13] 方法广泛应用于降低寿险公司的系统性死亡风险[14−16]和期权的套期保值研究[17−19]..许启发等[20]指出,完整地描述随机变量变动规律需要依赖于分布函数,而分位数回归能够揭示在不同分位点处变量之间的异质影响关系.这些研究表明,分位数回归不仅能像均值回归那样刻画平均套保比率,还能展示不同分布下极端分位的比率大小,从而实现更精准的套期保值.

然而,股票市场普遍存在着高波动状态和低波动状态,资产收益的均值和方差往往会随时间和市场状态发生变化,因此在套期保值时需要考虑市场所处状态.Sephton[21]研究指出,马尔科夫状态转换(MRS)模型可以适度控制状态变化的频率,同时有效捕捉市场状态的特性,从而将整个市场波动样本划分为多个子周期.运用MRS-OLS 模型,Alizadeh 等[22]研究富时100 和标普500 指数期货的套期保值比率发现,MRS-OLS 套保效率优于OLS 模型和ECM 模型.赵华等[23]分析常转换概率和时变转换概率下中国铜期货市场的套保比率,结果表明,两种概率下高波动状态的稳定性、持续时间均低于低波动状态,状态转换的套期保值模型均优于单一状态套期保值.

考虑现货和期货数据协整关系保持不变,偏离长期均衡状态的误差修正项受马尔科夫链控制且具有时变性,学者们使用MRS-VECM 模型研究现货和期货市场的动态关系.Chiang 等[24]研究发现,MRS 协整方法的均方误差远小于传统协整方法,更能反映股票指数与期货间的长期关系.Li[25]假设期现市场间的套利行为会增加两个市场的波动性,将滞后期期货和现货价格偏差的绝对值作为市场方差指标,在计算时变转换概率时赋予近期市场动量更大的权重.对美国标普500、英国富时100 和德国DAX 30 指数现货和期货研究表明,高波动状态下套利交易引起的价格调整规模大于低波动状态.该方法的局限性在于,外生设定滞后期期现价格偏差的权重,导致市场不论t −1 时刻处于何种状态,t时刻处于高波动状态的概率都会增加.Hache 等[26]运用短期残差的方差协方差矩阵计算短期MRS-VECM 模型,分析两种状态(标准状态和危机状态)下WTI 原油现货和期货价格的动态关系,发现投机交易会增加危机状态出现的概率.Balcilar等[27]和Allen 等[28]应用MRS-VECM 模型进一步分析原油期现价格间的格兰杰因果关系.现有研究表明,MRS 模型通过引入波动和协整之间的信息联系,允许期现收益均衡关系的调整随时间变化,可以灵活应用于多种期现市场关系的研究.

从上述研究可以看出,由于指数期货和现货收益率之间的关系既会随分位不同发生变化,也会随市场所处波动状态的不同而改变,因此同时考虑不同市场状态下最优分位数套期保值是一个改进的方向.本文在分位数回归基础上,构建基于马尔科夫状态转换的分位数回归模型.主要工作如下:第一,将Shrestha等[12]的分位数回归拓展至高、低波动状态,允许不同分位点上的套保比率依赖于状态变化,考虑市场新信息的加入对分位数套保比率的影响.第二,不同于Li[25]、Hache 等[26]研究方法,本文没有限定转换概率的滞后期权重或使用短期模型,而是采用一般化MRS-ECM 模型,使所有参数同时随市场状态和分位不同而变化,可以更细化地计算套期保值比率.第三,为进一步验证分位数回归相对均值回归的优势,不仅计算了Shrestha 等[12]提出的分位数套保效率,还基于损失函数最小化法给出最小方差套保效率的分位数计算方法.本文将以上方法应用于中国股指期货套期保值研究,计算基于马尔科夫状态转换的最优分位数套期保值比率及其效率.结果发现,在高波动状态和低波动状态下,分位数套期保值均优于最小方差套期保值.

2 套期保值比率的计算方法

令St和Ft分别表示t时刻下现货和期货价格,∆St=ln(St)−ln(St−1)和∆Ft=ln(Ft)−ln(Ft−1)分别表示t −1 至t时刻现货和期货的对数收益率.

2.1 单一状态套期保值模型

2.1.1 最小方差套期保值比率

假设H为套期保值比率,在套期保值中投资者持有的期末组合收益率为RHt=∆St −H∆Ft.最小方差套期保值比率(HMV)可以通过最小化RHt方差得到

为了估计HMV,建立∆St关于∆Ft的回归模型

其中α为截距项,εt为误差项.

采用OLS 方法得到的β估计值即为HMV估计值.

当期货和现货收益序列之间存在协整关系时,OLS 模型估计出的套保比率是有偏的.为此,可引入误差项建立误差修正模型(ECM)估计套保比率,即

基于ECM 模型的套保比率估计值即式(3)中β的估计值,记为HECM.式(3)中∆St和∆Ft的滞后阶数由AIC 信息准则确定.

2.1.2 分位数套期保值比率

分位数回归是由Koenker 等[29]提出的一种半参数回归方法,旨在寻找每个分位点下因变量条件分布与自变量之间的关系.在线性分位数回归中,随机变量Y的连续累积分布函数为FY(y)=Pr(Y≤y).Y的第τ个分位值为

假设L(θ(τ))表示期望损失函数,参数θ(τ)可以表示为

通过线性规划法可以得到参数θ(τ)的估计值

LS(θ(τ))是参数θ(τ)的样本损失函数,下标S 指样本.

Koenker[30]证明,在误差项独立的弱条件下,参数向量θ(τ)的估计值是渐近正态的,可以使用自举法计算分位数回归参数及其置信区间.

2.2 考虑状态转换的套期保值模型

由于资产收益在不同市场状态下表现出不同的分布形态,因而在动态套期保值中需要考虑市场状态转换.Hamilton[31]应用Goldfeld 等[32]的马尔科夫状态转换模型分析非平稳时间序列和经济周期,提出使用最大似然法估计离散的不可观测状态.本节引入马尔科夫状态转换模型,估计ECM 模型的最优分位数套期保值比率.

基于状态转换的ECM 模型表示为

其中下标Mt是t时刻的不可观测状态变量,Mt=1,2,...,k(k为状态的数量,本文取k=2)2Hamilton 等[33]指出,引入两种状态的MRS 模型足以恰当区分不同波动率水平.基于此,本文直接使用两种状态的MRS 模型研究市场处于不同波动状态的套期保值比率,而不考虑更多状态..αMt是状态Mt的截距项,βMt是状态Mt的套期保值比率,γMt是状态Mt残差项ut−1的系数,εMt,t是服从正态分布的误差项,表示状态Mt下误差项的方差3假设期货收益和现货收益滞后项阶数在状态转换前后一致,协整检验证明该假设成立,这与Li[25]相符.因此式(3)、式(7)和式(9)使用相同的∆St 和∆Ft 的滞后阶数..

假设状态转换服从一阶马尔科夫过程,从t −1 时刻的l状态转变为t时刻h状态的转换概率为plh=Pr(Mt=h|Mt−1=l),满足l=1,2;h=1,2;pl1+pl2=1,ph1+ph2=1.

状态h处∆St的条件密度函数为

以每种状态的概率作为权重,对各状态的密度函数加权平均,得到整个样本的似然函数.相应的对数似然函数为

由于转换概率无法直接观测,因而可以参考Perlin[34]方法,根据信息的到达情况计算概率Pr(Mt=h),然后最大化式(11)获得模型参数的估计值.

当计算出模型参数后,可以同时得到两种不同的条件概率:滤波概率和平滑概率.滤波概率是利用期初至t时刻信息(It)推断时点t的状态,记作Pr(Mt=h|It);平滑概率是利用全部样本信息(IT)推断时点t的状态,记作Pr(Mt=h|IT).本文参考Hamilton 等[35],考虑股市波动具有持久性,且高波动状态通常与特定经济事件相联系的特点,为清晰平稳地区分现货收益每个时点可能存在的状态,使用平滑概率作为状态划分标准4使用平滑概率计算状态转换概率的方法可见于其它MRS 套保文献,如文献[23,36,37].本文另外使用滤波概率计算MRS 分位数套保比率,发现使用滤波概率和平滑概率得到的实证结论一致.,以Pr(Mt=1|IT >0.5 为状态1,Pr(Mt=2|IT)>0.5 为状态2,将原始数据集划分为两个子集,每个子集分别用于估计对应状态的分位数套期保值比率.

假设考虑状态转换的分位数参数向量θMt(τ)=[αMt(τ),βMt(τ),γMt(τ),ϕMt,s(τ),ϕMt,f(τ)],βMt(τ)是状态Mt分位τ的套期保值比率.θMt(τ)的估计值由下式得出,即

2.3 套期保值效率

为比较不同套保方法的有效性,需要计算各分位点的套期保值效率.迄今为止,不同学者使用不同方法评价套保比率:林旭东等[9]考虑收益和风险因素,使用标准化均值作为衡量套期保值优劣的指标.Barbi 等[38]以套期保值风险(在险价值VaR、预期损失ES、指数风险测度ERM)减少的百分比衡量套保有效性.Shrestha 等[12]借鉴Johnson[1]和Ederington[39]的组合方差最小化法,提出损失函数最小化法测度分位数套保效率.综合上述研究,由于Shrestha 等[12]的方法度量了特定分位下的样本损失,与分位数回归的计算思路一致,因此本文使用该方法计算套期保值效率.

根据式(8),给定分位τ,通过最小化样本损失函数LS(θ(τ))求出套保比率后,分位数套期保值效率

其中Vhedge(τ)=minθ(τ)LS(θ(τ)),Vunhedge(τ)=LS(θ(τ))|θ(τ)=0.

Vhedge(τ)是特定分位τ下最优期货头寸的样本损失函数最小值,Vunhedge(τ)是不包含任何期货合约头寸(θ(τ)=0)的组合样本损失函数最小值.正如Koenker 等[40]提及,在分位数回归中,套保有效性是线性回归拟合优度R2的自然类比.因此,HE(τ)值越大,分位数套期保值比率越有效.

为了进一步验证分位数回归相对于均值回归的优势,需要另外计算均值回归的套期保值效率.林旭东等[9]将19 个分位点的标准化均值套保效率和OLS 模型单个的套保效率比较,得出基于分位数回归的套期保值优于静态套期保值的结论.这一效率比较方法忽略了不同分位间样本数据的差异性,不能准确衡量在各分位上使用最小方差套保比率的有效性.为此,基于式(13),本文给出最小方差套保效率计算公式

3 中国股指期货的最优分位数套期保值比率

3.1 数据描述及检验

本文选取上证50、沪深300 和中证500 指数的交易所交易基金(ETF),股指期货为样本.综合基金与期货的上市时间,沪深300 的期现样本区间为2012–05–28 至2019–06–21,上证50 和中证500 的样本区间为2015–04–16 至2019–06–21,数据来源于Wind 数据库.数据处理上,由于期货价格序列存在不连续性,本文使用向前比例调整法,在每月主力合约基础上构造出一个新的期货价格序列5考虑期货连续合约之间存在一定非价格行为的跳跃,两个合约的价格差会导致期货价格序列出现跳空现象,此时的收益不完全是真实收益.Masteika 等[41]指出,通过保持历史第一个合约价格不变,将最新的主力合约价格按缺口比例调整,可以估计投资者的真实收益情况,对于真实的交易活动应该使用比例调整法构建期货序列.因此,本文采用向前比例调整法处理期货数据..现货和期货的日收益率分别为∆St=ln(St)−ln(St−1),∆Ft=ln(Ft)−ln(Ft−1).

现货和期货日收益率数据的描述性统计如表1 所示.三组指数期现收益率均值接近0,上证50 和沪深300 期现收益率的波动程度相近,二者均小于中证500.观察偏度和峰度,所有序列的偏度均小于0,峰度远大于3,呈现左偏尖峰的特性.同时,所有收益率序列的JB 检验都在1%水平下显著,均不符合正态分布.

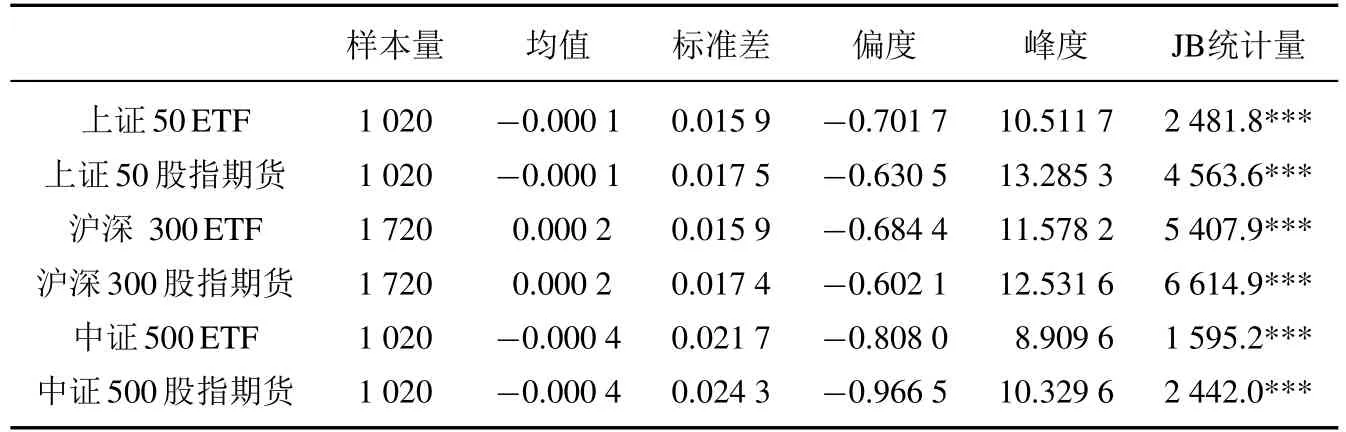
表1 现货和期货日收益率数据描述性统计Table 1 Descriptive statistics of spot and futures daily returns

为检验样本数据的平稳性,本文首先进行ADF 单位根检验,接着选用EG 协整检验法分析期现价格是否存在长期均衡关系.从表2 看出,三组期现对数价格的ADF 统计量均大于10%显著性水平的临界值,无法拒绝存在单位根的原假设,表明对数价格序列都是非平稳的.然而,一阶差分序列∆St,∆Ft在1%显著性水平下拒绝原假设,说明收益率序列平稳,三组对数价格均为一阶单整序列.EG 检验结果显示,三组期现价格间存在协整关系.

表2 单位根检验及协整检验结果Table 2 Results of unit root test and cointegration test

3.2 单一状态的最优分位数套期保值比率

本文分析19 个分位点上的套期保值比率,包括0.05,0.1,0.15,0.2,0.25,0.3,0.35,0.4,0.45,0.5,0.55,0.60,0.65,0.7,0.75,0.8,0.85,0.9,0.95 分位.首先,使用分位数回归估计ECM 模型期货的分位数套期保值比率、最小方差套期保值比率及对应的95%置信区间,结果见图1.三大股指期货在各分位的套保比率均显著,数值多在0.8∼0.9 范围内,两端分位的比率较低,中间分位较高,呈倒U 型,U 型程度因不同期货而异,表明分位数套保比率取决于现货收益分布.

在0.1,0.5,0.9 分位,上证50 股指期货套期保值比率分别为0.935 3,0.935 6,0.924 8,最小方差套保比率HECM为0.870 9;沪深300 股指期货套保比率分别为0.907 7,0.908 2,0.880 7,HECM为0.853 8;中证500的套保比率为0.887 9,0.883 0,0.757 7,HECM为0.820 7,高分位的套保比率普遍小于低分位的套保比率,倒U 型走势明显.除中证500 的0.9,0.95 分位外,三种股指期货分位数套保比率大于HECM,说明经过误差修正后,股指期货在各分位上使用HECM对冲易导致套保不充分[11].

最优分位数套保比率的倒U 型走势表明,股市处于极端行情(0.1 分位以下或0.9 分位以上)时,与小幅震荡行情(0.1∼0.9 分位)相比,投资者只需使用较少的期货头寸即可对冲一单位的现货.从价格发现角度究其原因,中国股指期货市场交易者主要是机构投资者[42],与个人投资者相比,机构投资者更理性、消息更灵通[43].Shrestha 等[12]认为,当消息灵通的交易者获得了关于有效价格剧烈变化(极端分位点)的信息时,他们会因为丰厚的收益而有更多的动机使用该信息,加之期货市场具有低交易对手风险、高执行效率、高流动性的优势,他们会在期货市场上率先交易,导致期货价格变化程度与速度远高于现货价格.相反,当交易者掌握了有效价格微小变化的信息时,他们可能没有足够的交易动机.

图2 是分位数套期保值效率的计算结果,值越接近1 表示效率越高.上证50 股指期货的分位数套保效率值均在0.74∼0.75 范围内,各分位的套保有效性差异较小.沪深300 在小幅震荡期的分位数套保效率值均在0.70∼0.72 范围,两端套保效率值较高.中证500 的套保效率呈U 型,且下凸程度较大,不同分位的套保效率差异明显.三种期货每个分位点上的分位数套保效率均高于最小方差套保效率,因此,使用分位数回归进行套期保值优于传统均值回归.

3.3 基于状态转换的最优分位数套期保值比率

金融市场中资产收益往往存在高、低波动状态的转换,而状态的变化通常是无法直接观测的.为深入探讨时变套期保值比率,本文引入马尔科夫状态转换模型,将样本数据划分为低波动状态和高波动状态,分别对应状态1 和状态2,并在此基础上计算各状态的最优分位数套期保值比率.三种指数的状态样本量如表3所示,低波动市场的存续时间总是长于高波动市场.

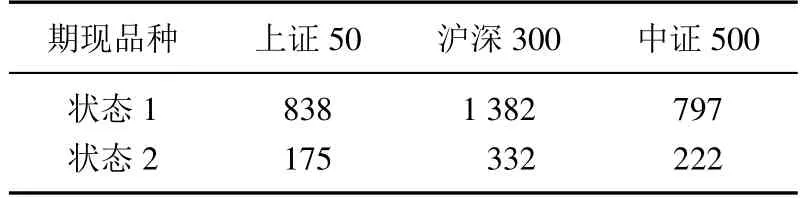
表3 三种指数的状态样本量Table 3 Regime sample sizes of three stock indexes

MRS-ECM 模型的最优分位数套期保值比率如图3 所示.状态1 的三组分位数套保比率较平稳,且套保比率值多大于0.9,与HECM值接近,表明在低波动状态下,可以近似使用ECM 最小方差套保比率对冲各分位现货价格变化的风险.状态2 的三组分位数套保比率在现货收益分布中呈现向右下方倾斜走势,随分位上升套保比率曲折下降,这与全样本分位数套保比率的形状有所不同.同时,左端分位的套保比率大致位于ECM 套保比率虚线之上,右端分位的套保比率在虚线之下.例如,在0.1,0.5,0.9 分位上,上证50 的分位数套保比率分别为0.847 6,0.791 8,0.754 6,HECM为0.811 4;沪深300 的分位数套保比率分别为0.890 1,0.789 1,0.712 7,HECM为0.784 6;中证500 的分位数套保比率分别为0.829 1,0.795 4,0.710 0,HECM为0.775 1.

高波动状态的套保比率小于低波动状态的套保比率的现象与Alizadeh 等[22,36]研究结果一致.相对低波动状态,高波动时期期现收益率变化的相关性短期内将下降,现货和期货价格会出现背离,导致不同状态的动态套保比率有所不同[36].此外,单一状态的分位数套保比率大小介于高、低波动状态的分位数套保比率之间,这是由于前者估计的是样本期内各分位点上的平均套保比率,而MRS 模型的套保比率会受到市场状态影响6由于单一状态、状态1、状态2 的样本数据集不同,若给定一个现货收益率,它在各状态的数据分布排列中处于不同分位点,可以计算出不同的套保比率,综合各分位点的套保比率会使整体呈现不同形状.因此,单一状态分位数套保比率呈现的倒U 型和状态1、状态2 形状不冲突..

考虑不同状态的分位数套保比率大小的具体含义.低波动状态的分位数套保比率与HECM接近1,高波动状态的分位数套保比率和HECM远小于1.Shrestha 等[12]认为,若套保比率接近1,期现价格变化较接近,价格发现可能同时发生在期货市场和现货市场;若套保比率小于1,期货价格随有效价格变化而变化的程度和速度将显著高于现货价格,价格发现主要集中于期货市场.基于这一观点,可以认为,低波动市场的价格发现可能同时存在于期现市场,高波动市场的价格发现主要产生于期货市场.这与何枫等[44]关于2010∼2016 年沪深300 指数与股指期货的联动关系研究的结论:相比市场平稳波动时期,市场剧烈波动时期期货市场的波动对现货市场和期货市场本身的波动解释程度逐渐增加相符.

由于高波动状态的分位数套保比率大小存在差异,因此在不同分位点上期货价格的变化程度和速度与现货价格变化之间的关系也有所不同.可能的解释是:中国股指期货市场主要由相对理性的机构投资者组成,股指期货市场的处置效应小于现货市场7处置效应指投资者倾向于在亏损时继续持有头寸,盈利时过快卖出头寸以实现收益的非理性行为.Frazzini[45] 认为,处置效应会导致投资者对消息反应不足.,因此期货市场反映新信息的速度快于现货市场[42].然而,市场投资者对正面消息的关注度少于负面消息,并且对正面消息的反应较少,促使不同分位点上金融市场之间的依赖性不同[46].当有效价格剧烈下跌的负面消息来临,期货价格迅速下跌并传导至现货市场,现货价格下跌速度随之加快.相反,当有效价格急剧上涨的正面消息来临,期现价格之间的变化程度和速度差异较大,现货收益上涨速度较慢.因此,左端分位的最优分位数套保比率较高,右端分位的最优分位数套保比率较低.

基于两状态的分位数套期保值比率计算得出的套保效率结果见图4.当市场处于高波动或低波动状态时,三大股指期货的分位数套保效率都呈正U 型,两端高中间低,在0.5 分位附近取得最小值.三种期货状态1 的分位数套保效率基本在0.80∼0.96 区间,而状态2 的效率值多在0.53∼0.88 区间.比较分位数套保效率和最小方差套保效率发现,区分高、低波动状态后,在不同分位,尤其是在两端分位上,使用分位数套保比率进行套期保值优于最小方差套保比率.

4 结束语

本文提出基于马尔科夫状态转换的分位数套期保值模型,该模型不仅考虑了市场信息的加入对分位数套保比率的影响,也考虑了MRS 模型所有参数随分位变化的特点,能够在各类市场条件下提升套保有效性.通过使用最小方差套保效率的分位数计算方法,考虑不同分位点的样本数据差异,有助于准确比较分位数回归和均值回归的套保效率.基于中国股指期货的实证研究表明,相比低波动状态,高波动状态的分位数套保比率值显著受现货收益分布的影响,因此使用该模型进行套期保值能更全面地捕捉高波动市场期现价格剧烈变化的信息,适应多状态市场环境的变化.