考虑碳排放的多产品竞争设施选址问题研究

刘伟伟 王明征 胡祥培

(1.大连理工大学经济管理学院,辽宁大连 116024;2.哈尔滨工业大学(威海)经济管理学院,山东威海 264209;3.浙江大学管理学院,浙江杭州 310058)

1 引言

设施选址问题研究的是企业如何选择合适的位置开设设施,当为顾客提供产品或服务时,使其总利润达到最大.设施选址决策作为企业的长期战略,是企业生存根本之所在[1].经典的选址模型,例如覆盖问题、p-中值问题和无容量设施选址问题,均基于空间垄断的假设,即企业是市场的唯一参与者[2,3].然而,该假设在诸多实际问题中并不成立,例如加油站、超市和快递门店等设施的选址中,在新设施进入市场之前,通常已有一个或多个竞争设施存在.由于新企业未进入市场前,该行业产品供需是平衡的.新企业一旦进入,将与对手竞争市场份额,势必会打破原有平衡,形成新的市场均衡价格、产品交易量和生产量,达到新的平衡状态[4].因此,在设施选址问题中考虑到竞争对手的反应尤为重要.

竞争选址,研究的即为竞争环境下的选址问题[5].20 世纪80 年代后,竞争选址逐渐成为选址领域的热点问题,得到了较为广泛的研究[6−8].作为竞争选址问题的一种,带预见性的竞争是指企业在进入市场之前,已经考虑到竞争对手会紧随其后进入市场.此类问题被描述为Stackelberg 博弈[9],即双寡头垄断市场的主从博弈.在该博弈中,有两个行动者(称为领导者和跟随者)相继进行决策.领导者预料跟随者的反应,制定自己的最优决策;跟随者在观测到领导者的决策之后制定自己的最优决策.Hakimi[10]首次将这个模型引入到选址领域,领导者将跟随者的最优反应纳入到决策过程中,并采取最小最大策略来维护自己的利益.Miller等[11]研究了寡头垄断企业的选址及市场均衡集成问题.Fischer 等[12]根据序列行动和运输价格固定与否对双寡头竞争选址问题进行研究并提出两种模型.

近年来,随着全球对碳减排的日益关注,政府及消费者都在迫使企业减少碳排放[13].许多国家制定了政策和法律法规来约束碳排放量.厂商要想担负起应有的社会责任、保持竞争地位,着重考虑碳排放势在必行[14].如何实现碳减排以及评估实施碳减排对企业绩效产生的影响成为当今企业普遍关注的关键问题之一.Wu 等[15]认为运输是物流系统中环境污染的最大来源.Elhedhli 等[16]指出,通过策略上合理安排设施的位置,减少车辆的出行距离,可以对国家碳足迹的减少起到重要作用.由此,将碳排放约束应用于企业的选址决策中,对于低碳可持续发展,具有广泛的现实意义.目前,诸多研究已关注碳排放[17−22],但在设施选址问题中纳入环境因素的研究尚不十分丰富[23],在竞争设施选址问题中考虑碳排放的研究更是相对较少.Ghaddar 等[4]在政府的碳交易机制下研究了双寡头垄断企业的竞争设施选址问题,考虑了运输产生的碳排放,目标为企业利润最大化,但他们针对的是单一产品.

众所周知,顾客对服务与产品的需求往往不是单一的.随着企业生产经营的多元化,企业已向顾客提供多种替代和/或者互补产品.由于产品之间存在着替代或者互补关系,一种产品的价格会对另一种产品的需求量产生影响,甚至当一种产品的价格高至其需求为零时,该产品仍然对其它产品的需求产生影响,所以产品的需求量不仅受到自身价格的影响,也受到其它产品价格的影响[24].企业在设施选址时考虑到产品之间的替代或者互补关系具有重要的现实意义.如何将产品之间的替代或者互补关系及政府的碳排放政策融入竞争设施选址问题中为企业制定出最优的设施选址策略,以实现利润最大化,是本文解决的主要问题.由此,本文探讨了碳交易机制下的双寡头垄断企业的竞争设施选址问题,将运输碳排放及多种产品之间的替代或互补关系考虑在内.

多产品的需求-价格关系是选址决策制定的关键.产品之间替代或者互补关系的存在导致了需求-价格关系极其复杂,因此现有选址文献普遍采用仅在某个区域上有定义的需求函数,如线性需求函数.Soon等[24]通过实例论证了基于该类型的需求函数制定的决策可能是次优决策,表明了基于定义于整个非负价格区域上的需求函数制定最优决策的必要性.现有文献主要有两种定义于整个非负价格区域上的需求函数：一种是利用单片可微函数近似需求,如Cobb-Douglas函数[25]和Logit 函数[26].该类型的函数形式上简单易处理,却不能反映真实市场.例如,在Cobb-Douglas 模型中会出现当其它产品价格上升,产品的需求量趋于无限大的情形;一种是利用分片光滑函数近似需求,如Boyer 等[27]和Kubler 等[28],但它们具有与第一种函数类似的不可取的特性.Soon 等[24]提出了一个分片光滑的多产品需求函数–互补需求函数,该函数能精确刻画整个非负价格区域上的需求,且具有如单调性等从经济管理角度可取的性质.为了制定全局最优选址决策,本文基于互补需求函数研究考虑碳排放的多产品竞争设施选址问题.目前仅有Federgruen 等[29−31]基于互补需求函数进行研究,但他们针对产品定价,不涉及设施选址.

由上述分析,本文将能够反映市场情况的互补需求函数引入多产品竞争设施选址问题中,以此融入了多种产品之间的替代和/或者互补关系.基于互补需求函数,建立了考虑碳排放的多产品竞争设施选址模型,为双层规划,是强NP-hard 问题;为了有效求解该问题,利用Karush-Kuhn-Tucker 条件、大M 方法和McCormick 外逼近方法将双层规划转化为有界闭集上的0-1 混合整数凹规划,极大地降低了问题的求解难度,并提出具有全局收敛性的分支提升算法;通过对数值结果的讨论分析,本文为低碳可持续环境下的企业运营提供了决策参考.

2 考虑碳排放的多产品竞争设施选址模型

2.1 问题描述

考虑两家制造企业.企业F 已建立b(≥1)处设施生产并向n(≥1)个顾客点提供其所需的l(≥2)种产品(产品之间存在替代或者互补关系).企业L 打算进入市场与企业F 竞争市场份额,因此需要从m(≥1)处备选设施中确定开设的设施.每处潜在设施均有能力生产此l种产品,且均可将产品运输到各个顾客需求点,运输产品的过程中会产生碳排放.本文考虑政府的碳交易机制,即政府对企业L 和企业F 分别规定碳限额EL和EF,当碳排放量超过EL(EF)时,企业L(F)可以从碳交易市场上购买其所需的份额;当碳排放量低于EL(EF)时,企业L(F)可以将多余的份额在碳交易市场上卖出,获取部分收益.

企业L 和企业F 之间是Stackelberg 博弈,企业L 为领导者,企业F 为追随者.Stackelberg[32]最早引入该博弈,之后出现了诸多扩展[33,34].企业L 预测企业F 的反应,确定开设的设施、设施到顾客点的产品运输量及产品的价格策略,以实现自身利润最大化.企业F 在观察到企业L 的决策后,确定已建立设施到顾客点的产品运输量策略,以实现自身利润最大化.

2.2 模型建立

本文假设对于任意,非线性互补问题的解唯一且∈Ω,该假设成立的具体条件见3.1节.

由于诸多理论模型和实证研究中普遍采用仿射结构,因此本文针对给定的需求函数dj(p)为线性需求函数的情形进行分析.线性需求函数dj(p)的具体形式为

表1 符号说明Table 1 Symbol description

基于以上介绍,企业F 的利润最大化模型为(aF)

企业L 的利润最大化模型为(aL)

企业L 和F 的优化模型构成双层规划模型,上层是企业L 的优化模型(aL),下层是企业F 的优化模型(aF),这即为本文所建立的考虑碳排放的多产品竞争设施选址模型.上层模型(aL)为带均衡约束的0-1 混合整数二次规划,下层模型(aF)为带均衡约束的二次规划,且两个模型的目标函数中均含有非线性程度高的双线性函数,求解异常复杂,为强NP-hard 问题[37].

3 模型分析

为了提出有效的求解算法,本节对双层规划模型进行分析.3.1 节将双层规划等价转化为单层规划;3.2节利用大M 方法将均衡约束等价转化为线性约束;3.3 节通过利用McCormick 外逼近方法将目标函数中的双线性函数线性化,将模型转化为有界闭集上的0-1 混合整数凹规划.

3.1 双层规划到单层规划的等价转化

企业F 的最优决策,即模型(aF)的最优解可由Karush-Kuhn-Tucker(KKT)条件刻画,即

其中变量ρjk和σqk分别为对应于约束(2)和约束(3)的对偶变量.

由此,双层规划模型可以转化为如下单层规划模型(b)

若dj(p)为线性函数,则线性互补问题存在唯一解(即均衡约束(17)有唯一解)的充分必要条件是Aj是P矩阵[24].由此,本文余下部分假定为P矩阵1.

将模型(b)中的约束(6)和约束(13)替换为式(16)∼式(18),得到如下等价模型(c)

将双层规划转化为单层规划,求解难度在一定程度上有所降低,但此等价模型包含更多的均衡约束,即式(12),式(14),式(17)∼式(18),且其目标函数中有双线性函数,仍为强NP-hard 问题[38],求解难度仍不低.

3.2 均衡约束的等价转化

带均衡约束的优化问题一般难以求解,因为其可行域非凸甚至不连通.现实生活中,由于顾客对产品的需求量是有限的,所以(∀k ∈K)有上界.本节利用大M 方法[4],通过引入统一的系数M 及二进制变量,分别将均衡约束(12),约束(14),约束(17)∼约束(18)等价转化为线性约束,得到如下模型(d)

相比模型(b)的等价模型(c),模型(d)中不再含有均衡约束,结构更加明确,为带线性约束的0-1 混合整数二次规划.由于均衡约束的等价转化,则模型(c)与模型(d)是等价的.因此,可用求解模型(d)取代求解模型(b).注意到模型(d)的约束均为线性约束,则其约束集已为有界闭集,进一步分析模型(d)的目标函数,有下面的结论.

命题1模型(d)的目标函数不是凹函数.

命题1 的证明见附录.

为便于模型分析,将dj(p)的具体形式代入约束(16),约束(23)和约束(26)中,得到如下等价模型(e)

3.3 混合整数非凹规划到凹规划的转化

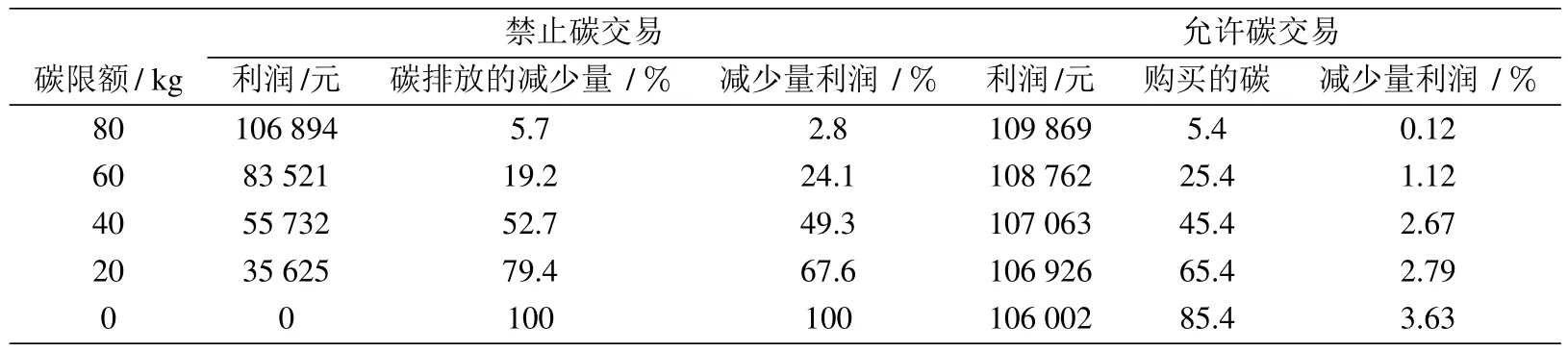
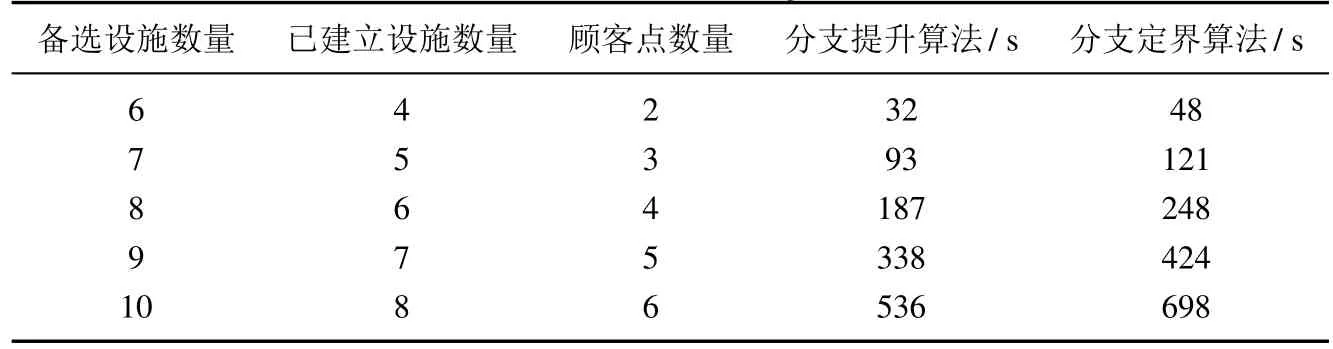
引理1满足Lx≤x≤Ux(Lx

确定的包络wxy.

与模型(e)相比,模型(f)目标函数中非线性项仅有. 此时进一步分析模型(f),有下列结论.

定理1模型(f)的目标函数为凹函数.

证明目标函数中的非线性项为二次项,其余项均为线性项.由于此二次函数是凹函数,从而目标函数为凹函数2虽然均导致模型(e)目标函数非凹,但当 被其McCormick 包络代替后,模型(f)的目标函数已变为凹函数. 因此本节仅对 线性化而未再对线性化.. 证毕.

通过上述分析,求解带均衡约束的0-1 混合整数二次规划(b),取而代之地求解有界闭集上的0-1 混合整数凹规划(f)即可,这极大程度地降低了问题的求解难度.

4 分支提升算法

相比原问题,模型(f)由于约束及引入的0-1 变量的增多,其规模更大.针对大规模0-1 混合整数凹规划(f),本节在分支定界的过程中通过不断更新McCormick 不等式产生更紧的外逼近来提升求解效率,由此称所提出的算法为分支提升算法.

4.1 分支和剪枝规则

为方便起见,本文求解与凹规划(f)等价的凸规划,记为(f′),其目标函数为模型(f)的相反数.记向量,i ∈I,j ∈J,q ∈Q,k ∈K及Ψ={ψ:Lψ≤ψ≤Uψ},其中Lψ和Uψ分别表示ψ各分量的下界和上界所组成的列向量.记向量ϕ=(z1,z2,...,zm),及Φ=[0,1]m,由于ϕ的各分量均为0-1 变量,所以其下界均为0,上界均为1.

从求解模型(f′)的连续松弛问题（即抛弃整数要求）开始.如果松弛问题不可行,则原问题不可行.否则,选择一个变量进行分支,产生两个子问题.在算法进行过程中,不断求解子问题,并通过分支添加新的子问题.当不再产生子问题时,算法终止.令LPR(Ψκ,Φκ)表示子问题的连续松弛,分别为其最优解和最优函数值,其中κ代表当前结点,Ψκ和Φκ代表当前可行解空间.

为保证求解的精确性,不仅对整数变量进行分支,还对连续变量进行分支,分支过程如下:若ϕς的值为分数,对其进行分支,即

类似地,对连续变量xς在值处进行分支,即

在分支过程中,交替选择整数变量和连续变量进行分支.之所以如此操作,是因为整数变量代表的选址决策与连续变量代表的定价与运输量决策之间相互影响.分支变量的类型一旦确定,再从中随机选择一个变量进行分支.为了产生更紧的外逼近,每次对连续变量进行分支后,均在子问题中更新McCormick 不等式(34)∼式(37).

4.2 算法步骤

基于上述表示,本节具体描述分支提升算法:

证明(f′)的下界和上界分别由松弛问题LPR(Ψκ,Φκ)和NLP(Ψκ,)的最优值给定.在可行解空间上找不到更好的解保证了剪枝规则(即情形1∼情形3)的合理性.为保证求解的准确性,对整数变量和连续变量均进行分支.由于整数变量的数量是有限的,则对整数变量进行的分支即为有限步.在对连续变量进行分支时,通过在子问题中更新McCormick 不等式,由此得到更紧的外逼近.则在有限步之后,(f′)与原问题之间的间隙一定小于给定的精度ε.因此,分支提升算法会在有限步之后收敛至最优解. 证毕.

5 算例仿真

5.1 数据选取

本文在主频3.4 GHz 的Intel i7 处理器,8 GB 的运行内存和64 位的操作系统下运行所有算例,在MATLAB 2014a 环境下执行求解的算法.针对两种可替代产品,假设企业L 的备选设施、企业F 的已建立设施以及顾客点均随机生成于(75×75)km2的区域上,利用欧几里得范数衡量设施与顾客需求点之间的距离.精度ε=10−6,M=1010.算例参数见表2,其中部分参数参考文献[4].

表2 模型参数Table 2 Model parameters

5.2 选址结果及分析

由表3,线性需求函数情形下,企业L 开设两处设施,并均提供产品1 和产品2,利润为19 963元;互补需求函数情形下,企业L 仅开设设施1且仅提供产品2,利润为22 501 元,比线性需求函数情形下的利润增加了12.7%.究其原因,对比表3 中的数据发现,两种需求函数情形下产品2 的价格均为380 元,产品1 的价格在互补需求和线性需求函数情形下分别为160 元和128 元.这意味着产品1价格的升高导致产品2的需求增加,而产品2 销量增加所带来的收益要高于线性需求函数两处设施同时销售产品1 的收益.发现d2(p1,p2)=2 400+30p1−20p2<0,即企业L 的最优决策在线性需求函数限定的价格区域之外取到.企业F 在两种情形下的供应策略在互补需求情形下的利润同样高于线性需求函数情形下的利润.因此,对产品价格进行限制进行会导致企业部分利润的流失,取到“次优”决策.进一步表明,企业在制定最优决策时考虑互补需求函数的必要性,即本文所提模型的合理性和有效性.

表3 最优选址、定价及供应量策略Table 3 Optimal location,price and quantity strategies

5.3 碳限额及碳交易对企业决策的影响分析

企业L 在最优选址决策下的碳排放量为85.4 kg.以企业L 为例评估碳限额对企业决策的影响.为了阐明碳限额的影响,考虑禁止碳交易和允许碳交易两种情形.将企业L 的碳限额由80 kg 开始依次减少20 kg 直至0,企业F 的碳限额仍保持在80 kg.对比禁止碳交易和允许碳交易两种情形下的结果,见表4.

表4 禁止碳交易和允许碳交易情形下企业决策结果对比Table 4 Comparison decision results under prohibiting carbon trading and allowing carbon trading

由表4,若政府禁止碳交易,碳限额的减少虽然会使企业碳排放量减少,但企业利润也会同步减少,这并不利于企业的发展.若政府允许碳交易,当政府给定的碳限额不足时,企业总会从碳交易市场上购买所需的碳使总量达到85.4 kg.有趣地是,企业并不会为此付出过高的代价,甚至当政府给定的碳限额为0 时,企业仅牺牲大约3.63%的利润即可获得额外所需的碳.由此表明,碳交易机制的实施对于企业的可持续经营以及整个国家碳足迹的减少起到了一定的作用,因为企业总会从碳交易市场上购买其它企业多余的碳满足自身生产活动,但只需牺牲微博的利润即可,这在一定程度上也减轻了企业对碳排放政策实施的担忧.

5.4 算法有效性分析

为了评估分支提升算法在处理大型选址算例上的表现,本节将分支提升算法与He 等[40]近期提出的一种分支定界算法在处理较大规模算例的时间作比较,结果见表5.

表5 分支提升算法和分支定界算法运行时间对比Table 5 Comparing the computational time of branch-and-refine algorithm and branch-and-bound algorithm

第1 列代表备选设施的数量;第2 列代表已建立设施的数量;第3 列代表顾客点的数量;第4 列和第5列分别表示分支提升算法和分支定界算法的求解时间.由表5,随着算例规模的增大,即备选设施数量、已建立设施数量和顾客点数量的增多,求解算例所耗时间增加.但相比分支定界算法,本文所提的分支提升方法仍具有优势.

6 结束语

在绿色低碳可持续背景下,随着现代经济的迅速发展和企业经营的多元化,制造多种替代和/或互补产品的企业在制定选址决策时预测竞争对手的反应至关重要.本文将政府的碳交易机制和产品之间的替代或者互补关系融入竞争设施选址问题中,建立了考虑碳排放的多产品竞争设施选址模型.针对模型特征,将其转化为有界闭集上的0-1 混合整数凹规划,并提出具有全局收敛性的分支提升算法.算例仿真结果表明企业总会从碳交易市场上购买其它企业多余的碳满足自身生产活动,但只需牺牲微薄的利润即可,这在一定程度上减轻了企业对碳排放政策实施的担忧,对于企业的可持续经营以及整个国家碳足迹的减少起到了一定的作用.本文假定顾客的购买意愿仅受到产品价格的影响,实际上消费者在购买产品时会关注产品的绿色水平,后续的研究将进一步在设施选址问题中考虑消费者的环境偏好.

附录 命题1 的证明

一个矩阵是半正定矩阵的充要条件是该矩阵的所有主子式非负.显然,该矩阵并不是半正定矩阵,因为存在负的主子式,如第1 行,第2mn+1 行和第1 行,第2mn+1 列构成的主子式.所以模型(d)的目标函数并不是凹函数.

证毕.