仓库容量有限条件下桂林米粉的生产销售存贮研究

任林洁 李丹 谢海斌

摘  要：桂林米粉作為广西旅游饮食的著名品牌之一，其销售存储策略直接影响商家的经济规模和经营效益。本文在仓库容量有限的条件下，建立不允许缺货的桂林米粉的生产销售存贮模型，通过计算得到该模型的最优存贮策略，并通过案例数据分析，说明结论在实际应用中的合理性。

关键词：存贮模型;桂林米粉;销售商;生产商

基金项目：2018年大学生创新创业项目;2017年广西高等教育教学改革工程项目（2017JGA376）;2018年校级项目：漓江流域旅游生态发展研究的阶段性成果。

引言

桂林旅游文化产业是广西旅游文化产业的重要品牌之一，需要不断优化产业结构，提升产业品牌效益和经营效益。桂林米粉是桂林饮食文化产业的著名品牌，每年吸引着大批游客和当地居民等消费群体，无论销售商还是生产商，都需要考虑销售过程中的最佳产品存储策略，进而提升桂林米粉的经营效益。而在实际生产经营中，为保留米粉的新鲜度，需要控制米粉存放时间，这就需要具备较大的库存空间，从而提升了运营成本，对于经营者而言，是否租借仓库来缓解运营成本压力，提升经营效益是值得研究的一个问题。

目前，国内外已有许多学者在存储策略及其应用方面进行了大量研究，如文献[1]介绍了经典的经济订货存储模型和经济生产存储模型，两种模型对仓库容量没有限制。然而在实际生活中，仓库容量往往是有限的，故文献[4-8]研究了仓库容量有限的条件下产品订货销售模型和生产销售模型。其中文献[4]给出了不允许缺货情况下使用租借仓库的订货存储模型，并给出了仓库容量有限的最优订货方案;文献[5]在文献[4]的基础上进一步研究了仓库容量有限的生产销售存储模型，并给出最优生产存储策略，并对比分析了使用和不使用租借仓库两种情况下的最优存储策略。需要注意的是在实际情况中，缺货产品有时无法得到及时补充，存在时间上的滞后性，故文献[6，7]进一步研究了允许缺货情况下的最优存储策略，文献[8]在文献[6，7]基础上对允许缺货的订货和生产存储模型进行了对比分析，并给出适合使用租借仓库的最优存储策略。本文将在仓库容量有限的条件下，从生产销售的角度建立不允许缺货下的桂林米粉销售存贮模型，并给出其相应的最优存贮策略。

一、模型假设

（一）在一定时间范围内市场对桂林米粉的需求率是稳定的;

（二）对于每一个生产周期，当米粉存储量为零时，立即得到补充，即不允许缺货;

（三）加工好的桂林米粉先存自己的冷藏室，若存放不完再考虑租借冷藏室存储;

（四）销售时先销售租借冷藏室内的桂林米粉，再销售自己冷藏室内的米粉;

（五）自己冷藏室的最大容量小于经典生产销售存贮模型的最大存储量。

二、仓库容量有限条件下桂林米粉生产销售的最优存储策略

如图1所示，设[T]表示桂林米粉生产周期，在备货时间[[0，t]]内，米粉加工店按生产率[M]进行加工生产，同时加工店还以销售率[Q]进行销售，故仓库的存储量以[M-Q]的速度增加;设[S0]表示加工店冷藏库的最大容量，[Smax-S0]表示加工店租借冷藏库的最大容量，在时间[[0，t1]]内，存满加工店自有冷藏库，在时间[[t1，t]]内存满租借冷藏库，且在[t]时刻停止加工生产;在[[t，t2]]时间段，加工店销售掉租借冷藏库中的米粉;在[[t2，T]]时间段，加工店销售自有冷藏室中的米粉，在[T]时刻所有冷藏库中的桂林米粉销尽。

图1 米粉加工店冷藏库米粉存储量变化图

根据已知条件可知  [t1=S0M-Q]，[t2=T-S0Q]，[Smax=（M-Q）?t]，

加工店在一个周期内的总加工量为[S=M?t][=Q?T]

设[R1]为加工店自有冷藏库的单位存储费，则在[T]内自有冷藏库的存储费用[D1]为

[D1=R10t1S0t1xdx+t1t2S0dx+t2TS0T-t2（T-x）dx]

[=R112S0t1+S0（t2-t1）+12S0（T-t2）]                  （1）

再将[t1=S0M-Q]，[t2=T-S0Q]代入（1）式可得 [D1=R1S0T-MS202Q（M-Q）]

设[R2]为加工店租借冷藏库的单位存储费，则在[T]内租借冷藏库的存储费用[D2]为

[D2=R2?12（Smax-S0）（t2-t1）]                        （2）

将[t1=S0M-Q，t2=T-S0Q，Smax=TQM-QM]代入（2）式可得

[D2=12R2?Q（M-Q）M?T2-2S0T+MS20Q（M-Q）]

此外在一个生产周期[T]内，加工桂林米粉还要包含的固定成本费[D3]，这样在一个周期内，加工桂林米粉所需要的总费用为

[D=D1+D2+D3]

[=R1S0T-MS202Q（M-Q）][+12R2?Q（M-Q）M?T2-2S0T+MS20Q（M-Q）+D3]  （3）

进而得到单位时间内的平均费用为

[R（T）=DT][=R2Q（M-Q）2M?T+MS20（R2-R1）2Q（M-Q）+D3?1T+（R1-R2）S0]    （4）

对函数[R（T）]求导，且令[dR（T）dT=0]，可以得到平均费用[R（T）]最小情况下所对应的最优生产周期

[T*=2D3MR2Q（M-Q）+M2S20Q2（M-Q）2（1-R1R2）]               （5）

进而根据[S=Q?T]得到桂林米粉在使用租借仓库的情况下的最优生产量为

[S*=2D3MQR2（M-Q）+M2S20（M-Q）2（1-R1R2）]                  （6）

结论：当桂林米粉加工厂存储桂林米粉的仓库容量有限时，可使用租借仓库存放桂林米粉。使用租借仓库时，桂林米粉的最优生产周期见（5）式，最优生产批量见（6）式。

三、算例分析与说明

通过数据调查与处理，得到数据如表1，对于桂林米粉加工厂，在保证经济效益最高的前提下，得出桂林米粉的最优生产周期和最优生产批量，从而得出桂林米粉加工厂的最优存储策略。

表1 计算桂林米粉加工厂最优方案数据表

[[Q]（筐/天） [M]（筐/天 ） [R1]（元/天[?]筐） [R2]（元/天[?]筐） [D3]（元） [S0]（筐） 180 267 0.4 0.8 1867 140 ]

在本例中有桂林米粉加工厂的最优生产周期

[T*=2D3MR2Q（M-Q）+M2S20Q2（M-Q）2（1-R1R2）] [=2×1867×2670.8×180×（267-180）+2672×14021802×（267-180）21-0.4/0.8][≈9（天）]

那么米粉加工厂在一个生产周期内的最优生产批量[S?]有

[S*=2D3MQR2（M-Q）+M2S20（M-Q）2（1-R1R2）] [=2×1867×267×1800.8×（267-180）+2672×1402（267-180）21-0.4/0.8][=1620（筐）]

那么米粉加工厂每天所需要最优平均费用[RT]为

[RT][=R2Q（M-Q）2M?T+MS20（R2-R1）2Q（M-Q）+D3?1T+（R1-R2）S0][≈370.02（元）]

这样在一个周期内，加工桂林米粉所需要的总费用[D]最小值为

[D=T×RT][=9×370.02][=3330.18（元）]

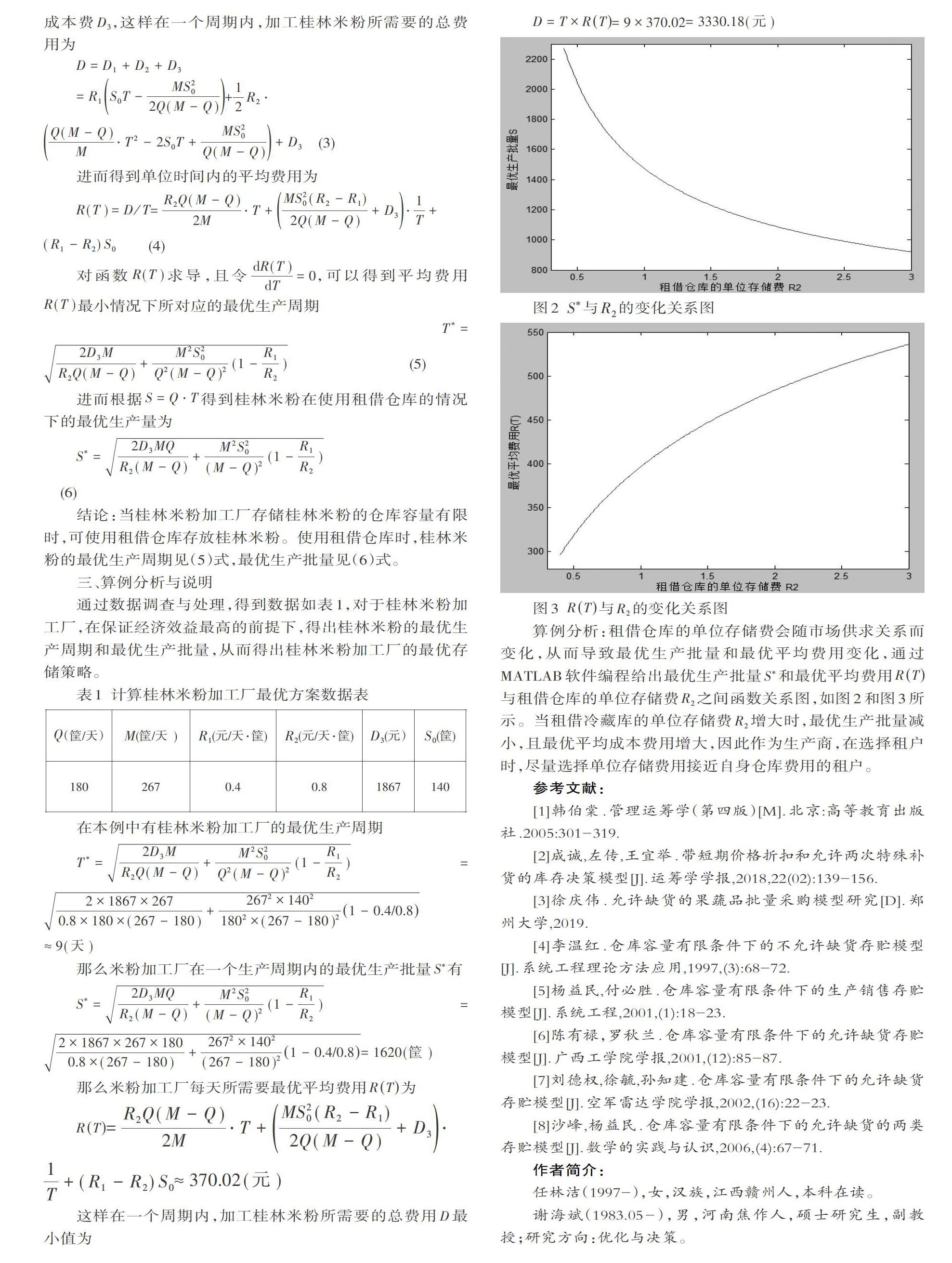
图2 [S?]与[R2]的变化关系图

图3 [RT]与[R2]的变化关系图

算例分析：租借倉库的单位存储费会随市场供求关系而变化，从而导致最优生产批量和最优平均费用变化，通过MATLAB软件编程给出最优生产批量[S?]和最优平均费用[RT]与租借仓库的单位存储费[R2]之间函数关系图，如图2和图3所示。当租借冷藏库的单位存储费[R2]增大时，最优生产批量减小，且最优平均成本费用增大，因此作为生产商，在选择租户时，尽量选择单位存储费用接近自身仓库费用的租户。

参考文献：

[1]韩伯棠.管理运筹学（第四版）[M].北京：高等教育出版社.2005：301-319.

[2]成诚，左传，王宜举.带短期价格折扣和允许两次特殊补货的库存决策模型[J].运筹学学报，2018，22（02）：139-156.

[3]徐庆伟.允许缺货的果蔬品批量采购模型研究[D].郑州大学，2019.

[4]李温红.仓库容量有限条件下的不允许缺货存贮模型[J].系统工程理论方法应用，1997，（3）：68-72.

[5]杨益民，付必胜.仓库容量有限条件下的生产销售存贮模型[J].系统工程，2001，（1）：18-23.

[6]陈有禄，罗秋兰.仓库容量有限条件下的允许缺货存贮模型[J].广西工学院学报，2001，（12）：85-87.

[7]刘德权，徐毓，孙知建.仓库容量有限条件下的允许缺货存贮模型[J].空军雷达学院学报，2002，（16）：22-23.

[8]沙峰，杨益民.仓库容量有限条件下的允许缺货的两类存贮模型[J].数学的实践与认识，2006，（4）：67-71.

作者简介：

任林洁（1997-），女，汉族，江西赣州人，本科在读。

谢海斌（1983.05-），男，河南焦作人，硕士研究生，副教授;研究方向：优化与决策。