子群的陪集与群的同构定理的几何解释
高印芝, 袁兰党
(1.河北师范大学数学科学学院,石家庄050024; 2.河北省数学与交叉科学国际联合中心,石家庄050024)
1 引 言
近世代数是以讨论代数体系的性质与构造为中心的一门学科.它运用具体与抽象、特殊与一般、有限与无限等辩证关系,用更抽象的严格的代数方法研究代数体系,对群的研究是该课程的重点. 为研究群的结构,利用子群给出了群的元素间的一个等价关系,这个等价关系将群中的元素进行分类,进而有了陪集的概念. 为研究不同群间的关系,揭示其本质,给出了特殊子群——不变子群,进而定义了商群. 近世代数研究的重要工具是集合、映射、同态、同构、等价关系. 下面先介绍相关的概念(见文献[1]).
定义1设G是一个非空集合,在集合G中定义运算“·”:任取a,b∈G,均有a·b∈G.若该运算满足结合律,即对于G的任意元a,b,c,均有(a·b)·c=a·(b·c),且对于G的任意元a,b,方程a·x=b和y·a=b在G中都有解,则称集合G关于运算“·”作成一个群. 如果群G中的运算“·”满足交换律,即对于G的任意元a,b,均有a·b=b·a,则称其为加群.
定义2若群G的非空子集H对于群G的运算“·”也作成群,则称H为群G的子群.进一步,如果H为群G的子群,且对G的任意元a,均有a·h·a-1∈H(a-1为a的逆元),则称H为G的不变子群,记作H◁G.
易见,加群G的每一个子群均为不变子群.
定义3设H是群G的子群,a∈G,称集合aH={a·h|h取遍H中的所有元素}为子群H的包含元素a的左陪集,集合Ha={h·a|h取遍H中的所有元素}为子群H的包含元素a的右陪集.
易证,(i) 对于G的元a,b,aH=bH的充分必要条件是b-1·a∈H;
(ii)对于G任意的元a,均有aH=Ha的充分必要条件是H为G的不变子群.
进一步,令H为G的不变子群,把H的所有陪集作成一个集合S={aH,bH,cH,…},定义S中的运算:aH·bH=(a·b)H,可以证明集合S关于该运算作成一个群,称之为商群,记作G/H.
以上概念都是很抽象的,没有具体实例是很难理解到其实质的,也就无从谈起将其应用到实际中去解决具体问题.
本文讨论的关于群的3个同构定理,就是研究群G、群G的不变子群以及商群间的重要关系,也是群论的重要内容之一,是教学的重点,也是难点.
本文将3个同构定理的内容对应到所熟悉的2维和3维空间以及其子空间(平面或直线)间的关系中,以其直观性来理解同构定理的内容,体会它们所揭示的问题本质.
2 相关结论的几何解释及意义
2.1 陪集的几何意义
令G=(3,+),H=(π,+),K=(L,+),则H,K均为G的子群,这里π,L依次为空间内过原点的平面与直线. 若β∈3,则陪集β+H是空间内包含β平行于π的平面π′(如图1所示). 陪集β+K是包含β平行于L的直线L′(如图2所示). 这是因为,如果α∈π,γ∈L,则由平行四边形法则,β+α∈π′,β+γ∈L′.
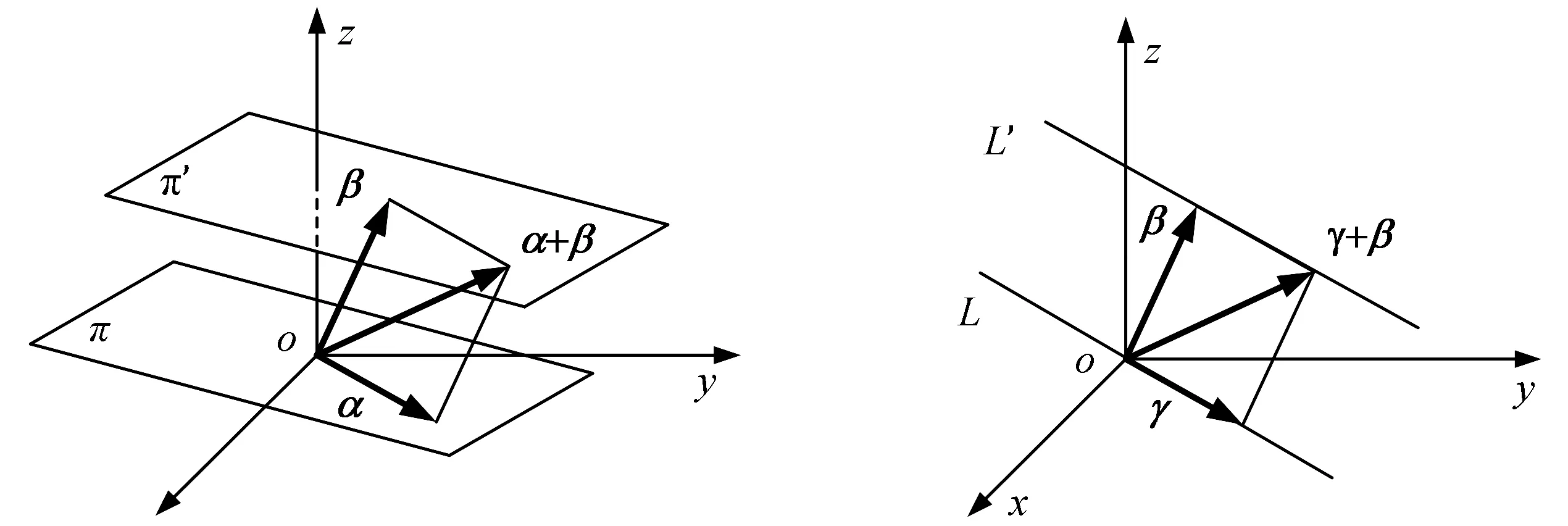
图1 图2
令(G=2,+),K=(L,+),则K为G的子群,这里L为平面内过原点的直线.若β∈2,则 陪集β+K是平面内包含β平行于L的直线L′(如图3所示).

图3
2.2 同构定理的几何解释
定理1[1]设G和H是两个群,并且G与H同态,那么这个同态满射的核N是G的一个不变子群,并且G/N≅H.
在定理1中,设(G=2,+),H=(x轴,+). 令f∶ (a,b)→(a,0),易知f为G到H的同态满射,同态满射的核N为y轴,且N为G的不变子群.
商群G/N为平面内平行于y轴的直线族:{x=a|a∈}. 令σ∶直线L∶x=a→点M∶(a,0),则σ为G/N与H间的同构映射.
若设(G=3,+),H={πa|πa∶平面x+y+z=a,a∈},且规定H的运算:
πa+πb=πa+b,
显然结合律成立,且对任意的πa:π0+πa=πa,πa+π-a=π0,这样H构成群.令φ∶点(x,y,z)→平面πx+y+z,显然φ为(G=3,+)到H的一个映射.
任取平面πa:x+y+z=a上的一点(x0,y0,z0),则(x0,y0,z0)→πx0+y0+z0=πa,所以φ为(G=3,+)到H的一个满射. 另一方面
(x1,y1,z1)→πx1+y1+z1, (x2,y2,z2)→πx2+y2+z2,
由
(x1,y1,z1)+(x2,y2,z2)=(x1+x2,y1+y2,z1+z2),
易知φ保运算,所以(G=3,+)与H同态,同态核N为平面π0:x+y+z=0上的点集.这里G/N为空间内平行于π0的平面族. 由定理1知,G/N≅H,事实上G/N=H.
定理2[2]如果H,K是G的子群,满足H◁G,则HK是G的子群,(H∩K)◁K,并且
K/(K∩H)≅HK/H.
在定理2中,令(G=3,+),H=(L1,+),K=(L2,+),L1≠L2,则HK=(π,+),这里π为L1与L2所确定的平面;H∩K={(0,0,0)},K/(K∩H)=K,HK/H为平面π内与L1平行的直线族.这样K≅HK/H,其同构映射为:L2上的一点M与平面π内过点M与L1平行的直线L′对应.即M→L′(如图4所示).
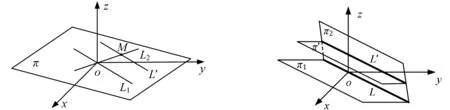
图4 图5
若令H=(π1,+),K=(π2+),π1≠π2,则HK=G,H∩K=(L,+),这里L为π1与π2的交线.K/(H∩K)为平面π2内与L平行的直线族.HK/H为空间内与π1平行的平面族.f∶L′→π′为K/(K∩H)与HK/H间的同构映射(如图5所示).
定理3[3]如果H,K是群G的不变子群,且K是H的子群,则H/K是G/K的不变子群,且
在定理3中,令(G=3,+),H=(π,+),K=(L,+),L⊂π. 则G/K为空间内与L平行的直线族;H/K为平面π内与L平行的直线族;G/H为空间内与π平行的平面族,且
这里β+H/K为平面π′=β+π内平行于直线L的直线族(如图6).
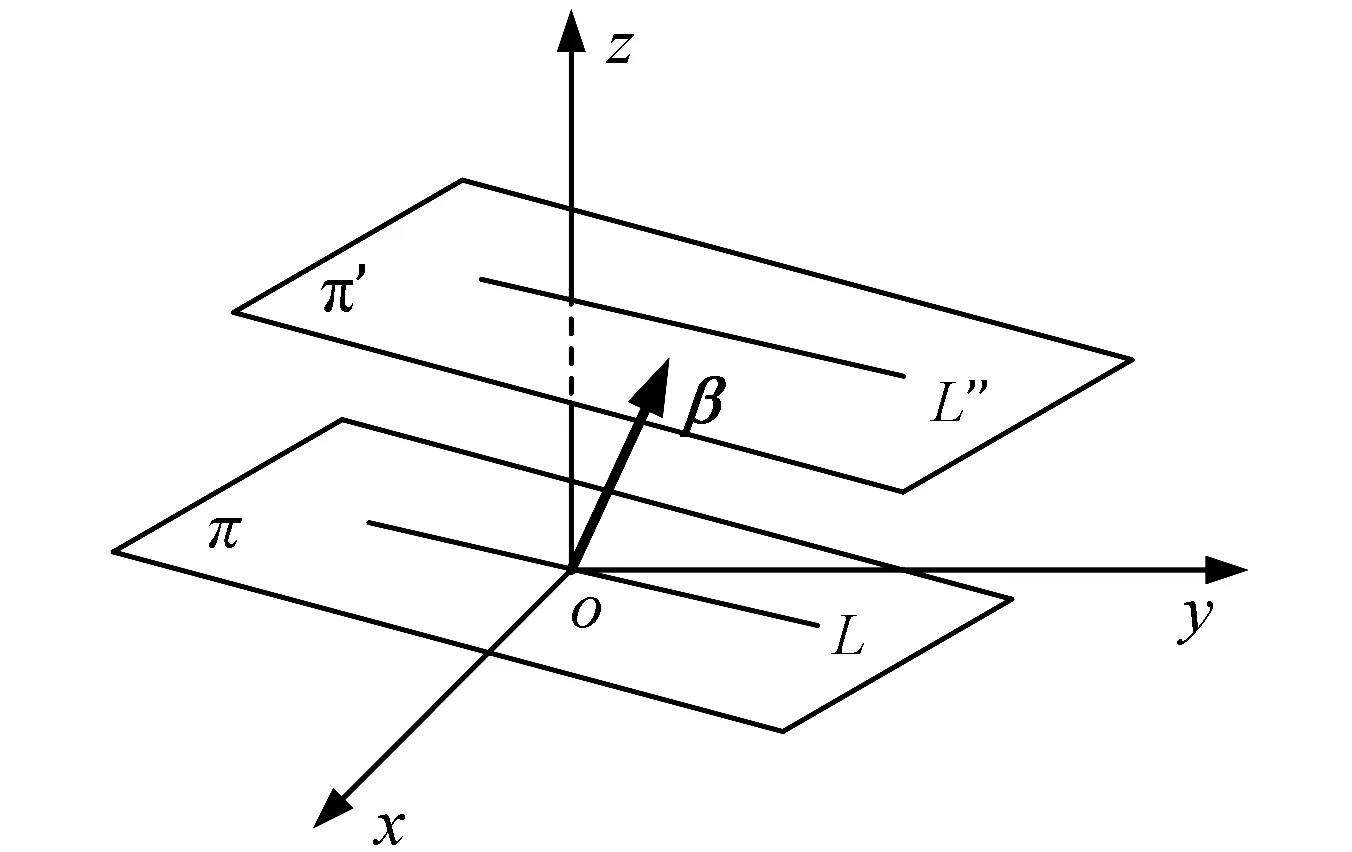
图6
对任意L″∈π′,由于L为过原点的直线,L″平行于L,所以L+L″=L″,于是
{L+(β+H/K)|β∈G}={β+H/K|β∈G}

3 结 论
正如引言所说,近世代数是以讨论代数体系的性质与构造为中心的一门学科,主要研究群、环、域等,其主要特点就是抽象,这体现在概念、定理和结论上. 这就使得初学者倍感迷茫,所以教学中教师常采用适当的方式解释抽象的概念,以帮助学生理解,如文献[4-5]中就有相关学习方法介绍或用具体的代数结构来诠释抽象的概念,以达到理解其本质的目的. 如整数集合、置换集合、矩阵集合及向量空间等. 本文的特点是利用几何空间中的直线与平面作为特例,尤其是借助几何图示诠释了抽象的陪集及同构定理.在教学中笔者总是用具体的、直观的例子解释抽象的概念及其逻辑关系,目的是调动学生学习的积极性,增强学习的兴趣,进而对看似枯燥的数学研究对象有更深刻的认识. 我们的学生越来越喜欢数学和热爱数学是我们数学工作者的目的所在.
致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.
——以指数、对数函数同构问题为例

