多种计算方法下自然常数e的误差和收敛速度比较

朱德凯，苏岐芳

（台州学院 电子与信息工程学院，浙江 临海 317000）

0 引言

自然常数e是继π后人类发现的又一个超越数，其最初的定义源自金融领域以及计算机领域对两个问题的解决［1］，后来在自然科学、工程技术等领域中的许多问题也运用到e的近似值，如力学欧拉公式、衰变定律［2］、牛顿冷却定律［3］等。自然常数e在不同领域有着广泛的应用，对其进行正确、快速的估计是非常重要的。

各高校的“数学分析”教材里均给出了自然常数e的原始定义［4］：

采用式（1）的计算方法，考虑其误差

从式（2）中可以看出，该算法收敛速度较慢，因此引入其他计算方法非常有必要。下面列举几种现有的计算方法［4-8］：

其中，式（3）的算法利用了Taylor展开式，式（5）的算法利用了积分上限，两种算法分别对自然常数e进行了估计。但文献［4-8］中并未解决对式（4）、式（5）算法的误差估计以及对式（6）算法的证明，本文将对此进一步进行理论和实验分析。

1 误差及其收敛速度的理论分析

1.1 式（3）算法的分析

由“拉格朗日余项”可知，式（3）算法的误差为

将式（7）与式（2）的比值取极限，易得

从而说明式（3）算法的收敛速度比式（1）算法的收敛速度快。

1.2 式（4）算法的分析

1.3 式（10）算法的分析

由于式（5）算法和n没有关系，但能够初步确定2＜e＜3，由“闭区间套定理”受到启发，构造一个闭区间套{[an,bn]}，其中a1=2,b1=3，接着每次取中点m，并查看两式

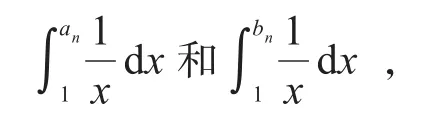
观察哪一个更接近于1，就选择其上限和m构成一个新的闭区间，反复操作便可得到{[an,bn]}。由于迭代初始端点值为有理数，所以经过有限次迭代后得到的闭区间端点值也均为有理数，并且有：

上述算法的收敛速度即为二分法的收敛速度［9］，误差为

将式（13）与式（2）的比值取极限，易得

将式（7）与式（13）的比值取极限，易得

从而说明式（5）算法的收敛速度比式（1）算法的收敛速度快，比式（3）算法的收敛速度慢。

1.4 式（6）算法的分析

首先，证明式（6）算法的合理性。

再利用两次stolz公式得到其极限值:

于是可得

即式（6）算法得证。

接着，得出式（6）算法的误差为：

不难看出，式（6）算法是比较繁琐的，难以找到其误差的等价量，但是能够定性分析其收敛速度一定不快，后续将继续进行实验分析。

2 误差及其收敛速度的实验分析

由式（8）、式（12）、式（14）、式（15），已经得出式（4）算法、式（1）算法、式（5）算法、式（3）算法的收敛速度是依次递增的，而式（6）算法的收敛速度待确定。为此利用MATLAB程序来更直观地展示上述5种算法的收敛速度和误差情况。

由于不同算法迭代所需要的时间大不相同，考虑到计算机计算的时间，在此先将误差限设置为10-1，采用MATLAB代码编程得到5种算法收敛情况的对比，如图1所示。

图1 5种算法收敛情况对比图

通过观察图1中极限值曲线的增长情况以及误差曲线的递减情况，能够确定式（6）算法的收敛速度＜式（4）算法的收敛速度＜式（1）算法的收敛速度，并且均比式（3）算法和式（5）算法的收敛速度慢。再将误差限设置为10-5，单独比较式（3）算法和式（5）算法的收敛速度，采用MATLAB代码编程得到这两种算法收敛情况的对比，如图2所示。

图2 两种算法收敛情况对比图

从图2可以看出，式（5）算法的收敛速度小于式（3）算法的收敛速度。综上所述，实验所得结果与前面的理论分析结果是一致的。

3 算法的改进

经过理论分析与实验计算，得出式（3）算法的收敛速度是最快的，但是通过观察发现其有两个缺点：①该算法涉及到“阶乘”，它会大大地增加计算机运行的时间。②该算法需要利用“循环语句”进行不断地迭代，其中每次迭代都是在后面加上一项，随着n的增大，会迅速减小，这会导致在进行精细运算时产生较大的误差。

为了避免以上两个缺点，需进一步优化改进算法，在此给出如下算法［4］：

设有a1=1，an=n(an-1+1)，n=2,3,…,于是

现给出式（17）算法的证明如下：

4 式（17）算法的实现

考虑到算法的实用性，将计算误差控制在小数点后15位，在此给出式（17）算法的MATLAB编程代码如下：

通过上述代码对e进行估计，得到：e=2.71828128245904……。若将误差限设置为小数点后15位，式（3）算法所需运行时长为0.001954 s，而式（17）算法所需运行的时长仅为0.000788 s，说明式（17）算法最优。

5 结语

本文通过对自然常数e的5种算法进行理论和实验分析，并经过改进与优化后，得到的新算法有效地避免了原有算法中存在的问题，同时节约了计算机运行的时间，提高了使用效率。