类比概括 回归本质——“弧度制”教学实录

宫建红

(1.华东师范大学教师教育学院，200062;2.江苏省扬中高级中学,212200)

章建跃博士说过:“概念教学的核心就是概括,概念教学要让学生经历概括的过程,要精雕细琢地设计概念的概括过程”.数学概念的教学核心是培养学生数学抽象的能力,让学生体会从具体感知到抽象形成的完整过程.本文以“弧度制”的教学为例，以背景——定义——表示——联系——应用为主线,从度量的本质出发,引导学生经历整个定义生成、知识建构的过程,探索概念教学的方法和具体的教学环节.现将教学过程记录如下,以供交流研讨.

一、 创设情境，建构定义

环节1 梳理体系,形成大观念

师:上节课我们对角的概念进行了推广,从静态地刻画角变成了动态刻画;知道了描述一个任意角,需要两个关键因素是——旋转方向和旋转量;并对任意角进行了分类,分为——正角、零角和负角.在实际生活中,尤其是在天文、航海、测绘等方面有着非常广泛的应用,因而还需要对角进行定量表示以及数据运算.今天,我们就一起来探讨角的度量问题.

环节2 提出问题,回到最近发展区

问题1怎样度量一个角的大小?(PPT)

师:给你一个角,你会度量它的大小吗?

生(齐):用量角器.

师:这里运用的是“角度制”,以周角的1/360为1度的角,用度作为单位度量角的大小,并规定:60′=1°,60″=1′.因此，角度制是多少进制?

生:60进制.

师:这种“以角量角”的度量方法起源于古巴比伦.为什么将圆周角等分成360份,说法很多,但都无从考证.可以考证的是当时对弧长、半径等长度的度量也是采用的60进制.

环节3 分析旧知,构建概念同化基础

师:从三角学的发展历史看,三角学是依托圆而存在的.因此,我们可以采用等分的思想,先定义度量的单位——1度的角,再进行度量.尽管“角度制”的定义依托圆周,但一定大小的角与圆周的大小(即半径大小)是无关的.大家一定都记得,在小学时的一个实验:用大小不同的量角器去度量同一个角,大小不变,这是“角度制”定义合理性的一个有力证明.(同步板书)

环节4 创设情境,形成认知冲突

师:角度既可以度量角,也可以进行运算.

情境129°28′46″+48°51′36″=?

学生独立运算,给出答案 78°20′22″.(由于不是熟悉的十进制,没能快速报出答案)

师:如果是熟悉的十进制,计算速度就快多了.随着数学的飞速发展,人们发现使用10进制更为便捷.

情境2如图1所示,某航海家从A点航行一定的距离到达B点,已知他的起始位置和航行距离,怎么确定运动后航船的位置呢?

师:从地心观察,小船进行的是圆周运动,如果知道移动的角度,也就知道了经度和纬度,就可以进行导航了.这时还能用量角仪器量吗?

生:不能.

师:这时候“以角量角”行不通了,还可以用其它量去度量角的大小吗?

环节5 自主探究,建构定义

问题2还可以用其它量度量角的大小吗?

生:我觉得可以用半径r,弧长l来度量.因为角的变化与半径和弧长有关系：若角α给定,半径r越大，弧长l越大；若半径r给定，角α越大,弧长l越大.

师：能否用其它量来度量角的大小,且与圆的半径大小无关？

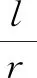
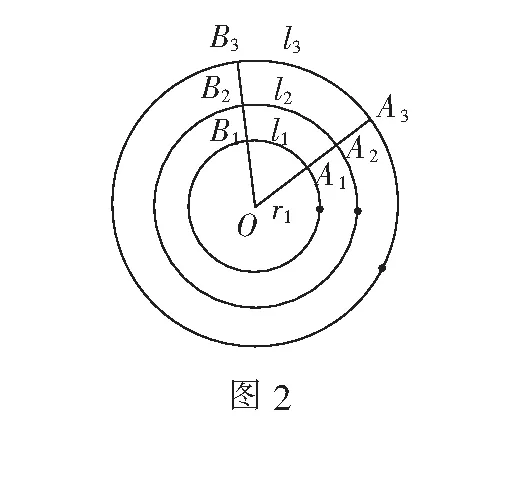
师:通过从特殊到一般的方法,发现弧与它所在圆的半径的比值是一个常数,与半径大小无关.

师:通过代数方法验证:利用已知的弧长公式,探索圆心角、所对弧长与半径之间的关系,发现圆心角所对的弧长与半径的比值随角的确定而唯一确定.

师:通过几何方法类比弦长/半径,得到弧长/半径也是定值.不论是特殊到一般、代数方法还是几何方法,都能得出共同的结论:同一个圆心角所对的弧与它所在圆的半径的比值是一个常数,与圆半径的大小无关.也就是说,角可以由弧长与半径的比值去度量,并且如此度量角的大小是唯一确定的.如果选取单位圆,取r=1,也就是可以用弧的长度去度量角的大小了,所以把这种用弧长去度量角的方式称之为“弧度制”.弧度制的本质是使用线段长度度量角的大小,这就是300多年前欧拉定义的“弧度制”,也是今天所要共同学习的“弧度制”.

问题3如何建立一种新的度量角的制度?首先要定义“单位”!

师: 如何定义1弧度的角呢?

生:弧长/半径值为1的角,称为1弧度的角.

师:把长度等于半径长的弧所对的圆心角叫做1弧度(rad)的角;特别地,在单位圆中，长度为1的弧所对的圆心角就为1 rad的角,用符号1 rad表示读作1弧度.因为弧长/半径,为两个长度之比,所以今后用弧度制表示角的时候,只要不引起歧义,“弧度”二字或“rad”通常略去不写.

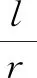
二、正例强化，理解定义

师: 如何用弧度制度量角呢?解决情境2中的问题.

师: 有了度量的单位,你能度量其它角吗?如图4所示(动态生成,考虑角的旋转方向)

生口答:∠AOB为1弧度角,∠AOC为2弧度角,∠DOA为-3弧度角,一周角为2π弧度角.

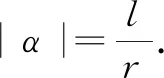
师:度量角我们可以用角度、弧度不同的单位制.生活中还有哪些是可以用不同单位制去度量的呢,你能想到吗?

生:度量长度可以用米、英尺、码、千米、公里、光年等;度量重量可以用千克、克、磅等.

师:我们知道一个量可以用不同的单位制来度量,不同的单位制各有优点,且互相可以转化,这样不同的单位制就给解决不同的问题带来方便.现在已经有了两种角的度量制,它们之间应如何换算呢？

问题4“角度制”和“弧度制”之间如何互相转化?

学生回答、总结角度与弧度的互化,明确核心公式π=180°，以及换算公式:

设计意图在建构弧度制的有关概念之后,应思考，对同一个数学对象从不同的角度去研究它,所得的结论一定有内在联系.所以引导学生发现联系两种度量制的桥梁，可以让学生进一步明确角度制和弧度制之间的联系,在此基础上深化对角度与弧度之间的关系的认识和理解.

三、数学运用，巩固深化

练习1特殊角的度数与弧度数的对应表(表1):

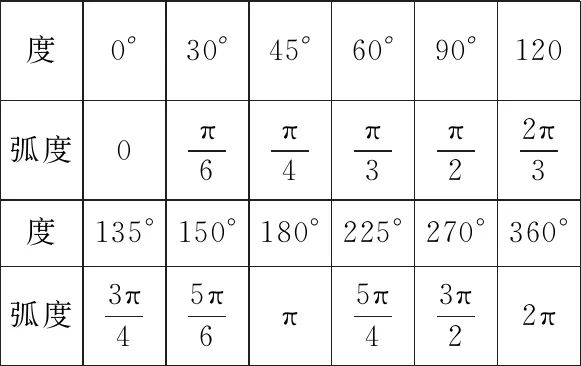
表1

练习2非特殊角的度数与弧度数的转化(例题略).

练习3引导学生推导在弧度制下的弧长公式和扇形面积公式:

师:弧度制下扇形的弧长公式、面积公式得到大大简化,这是弧度制优越性的又一个体现(表2).以后学到三角函数以及学习高等数学以后,还可以进一步体会到使用弧度制的优越性.

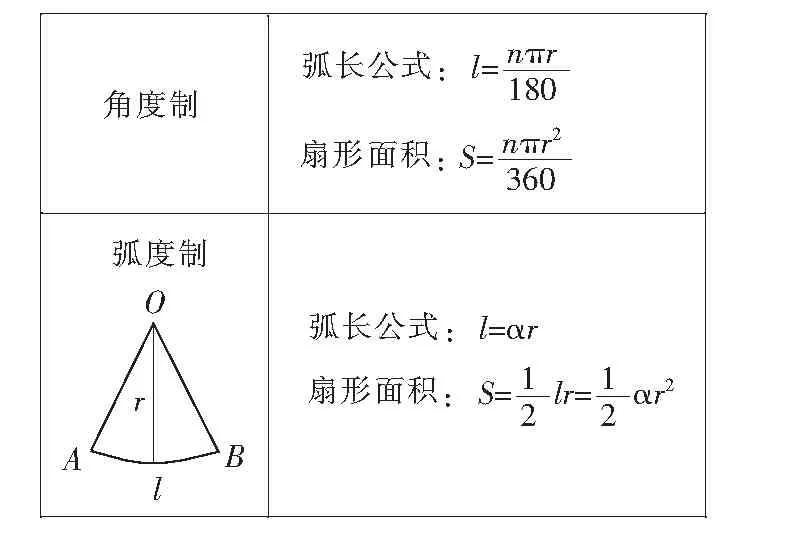
表2

设计意图数学知识的学习,需要与原有知识建立联系,在相互对比中思考其优劣,在寻求联系中完善其结构,在追求真实简洁、和谐美妙中培养学生的科学精神.这里,通过新旧知识的对比,让学生体会弧度制的优越性.在此环节重点突出以下两点:(1)角度制与弧度制的互化，紧扣360°=2π rad;(2)弧度制下扇形的弧长公式与面积公式的简洁性.

四、总结拓展，分层作业

师: “角度制”和“弧度制”之间有什么区别、联系呢?

学生回答,教师总结提炼,并完成黑板上的表格.

(1)角度制是以“度”为单位度量角的制度,弧度制是以“弧度”为单位度量角的制度;角度的单位不能省略,弧度的单位可以省略.

(2)角度制是六十进制的,弧度制是十进制的(弧度制优越性的体现).采用弧度制，任意角的集合和实数集可以建立一一对应的关系,即每个角都有唯一的实数与它对应,同时每个实数也都有唯一的一个角与它对应.

(3)不论是以“弧度”还是以“度”为单位的角的大小，都是一个与半径大小无关的定值;

(5)互化公式、弧长公式和面积公式.

师:本节课学习了哪些知识?掌握了哪些方法?体会了哪些思想?今后还要学习什么呢?

设计意图本节课类比长度和角度的单位制构建的过程,探究发现度量角的新单位制(弧度制),在角的集合与实数集R之间建立了一一对应的关系,可以为研究三角函数提供理论的准备,带来很大的方便.通过小结,引导学生进一步思考:构建一种单位制的一般过程,即从特殊事物中揭示一般规律,不仅要学习弧度制这方面知识,还要梳理、概括出研究过程是什么,促进学生明确研究内容,掌握研究的方法,体会研究的价值,感悟获得这些知识的心路历程.