组合计数推导法求多项式展开系数
赵 忆
(1.扬州大学数学科学学院,225000;2.江苏省丹阳市第五中学,212300)
一、问题陈述

北京卷、天津卷、上海卷的三道题都可以采用通项方法求解,但是对于浙江卷,由于多项式是(x-1)3,(x+1)4的和,套用通项公式就显得复杂,具体体现在以下几个方面.



从上述例子可以看出,机械地套用公式会将简单问题复杂化,同时还需要防止丢项、漏项及多个字母的混用等问题.
二、方法溯源
如何从根本上解决学生的困惑呢?需回归二项式定理的基本内容:



表1
这里,表格的使用克服了组合计数推导法书写繁琐、耗时长的缺点,使得抽象的组合计数推导法变得更加具体、清晰,且易于推广.
三、应用举例
例1求(3+2x)7展开式中x3的系数.
解两项和的展开,第一项为3,第二项为2x,求x3的系数,具体选取过程见表2表示.

表2

评析对于这种标准的二项式展开系数问题,通项公式法与组合推导表格法相比,虽然在解题繁简上没有明显区别,但是表格使得思维过程一目了然.
例2求(1+2x)3(1-x)4展开式中x3系数.

解两因式(1+2x)3,(1-x)4乘积,考虑x3的系数,x分别来自于两个因式,幂指数之和等于3即可,具体选取过程见表3.

表3

评析对于求(a+b)n(c+d)m两个因式乘积展开式中特定项的系数,通项公式法需对每个因式进行展开后再组合通项公式,再讨论求和,易导致缺项、漏项.采用表格,则每个构成项的系数都直接的展现出来,一目了然,具有一定的规律性,检查起来也更加方便.
例3求(x2+3x+4)4的展开式中x2的系数.



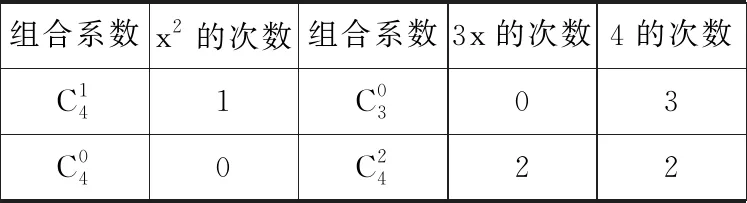
表4

评析对于求(a+b+c)n三项展开式中特定项的系数,通项公式法需将三项看成两项进行展开,并对其中两项部分再次展开,再讨论求和.该方法不仅繁琐,还夹杂着二元一次方程的求解,易导致缺项、漏项和字母的混乱.采用表格,则每个构成项的系数都直接展现出来,具有一定的规律性,可有效避免复杂的求通项的过程,解题步骤更加简明.
面对机械运用公式求解二项式定理展开式系数问题出现的解题困境,依据课标要求,回顾二项式定理推导过程给出组合计数推导法,并创造性地以表格的形式呈现出组合计数推导法,使得学生理解和书写起来更加直观具体,简单易懂.基于牛顿二项定理的组合推导表格法在知识层面上层层递进,在思想层面上循序渐进,在数学方法上由抽象到具体,彰显了数学文化在教学中的魅力,同时又展示了数学对简洁性的追求.
《普通高中数学课程标准(2017年版)》提出,“高中数学课程以学生发展为本……同时注重数学文化的渗透.”教师更应当注重数学文化的作用,结合学生的主体性地位,让学生经历数学家发现数学知识的过程,结合数学史,寻找数学家发现数学知识的历史渊源,再现人类发现数学知识的过程,让数学文化服务于数学课堂.

