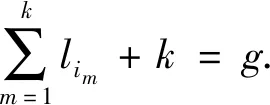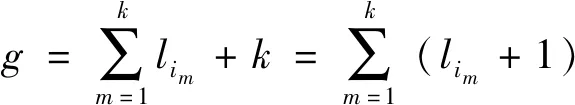斜秩等于围长的定向单圈图的刻画

王 震, 马晓玢

(安徽理工大学 数学与大数据学院, 安徽 淮南 232001)

记简单图G=(V(G),E(G)).如果G是一个连通图且|V(G)|=|E(G)|, 则称G是一个单圈图.本文考虑基于单圈图G的定向图Gσ, 即对任意不同顶点对u,v, 弧(u,v)∈E(Gσ)与弧(v,u)∈E(Gσ)至多只有一个成立.定向图Gσ的斜邻接矩阵定义为一个n×n矩阵S(Gσ)=(suv), 其中suv=-svu=-1当且仅当(u,v)∈E(Gσ), 否则suv=0.任意定向图的斜邻接矩阵都是反对称的, 从而斜秩总是偶数.如果图Gσ中的一个顶点的度为1, 则称该顶点为悬挂点, 与悬挂点邻接的顶点称为拟悬挂点.图Hσ称为图Gσ的导出子图, 如果H是G的一个子图, 并满足: 对任意顶点对u、v∈V(Hσ), (u,v)∈E(Hσ)当且仅当(u,v)∈E(Gσ).本文中, 图Gσ中的两个顶点u和v之间的距离指它们在底图G中的距离, 记为d(u,v).若Hσ是Gσ的子图且u∈V(G)V(H), 记d(u,H)=min{d(u,v),v∈V(H)}.定向图Gσ的围长是其底图G的围长,即G中最短圈的长度, 记为g(G).

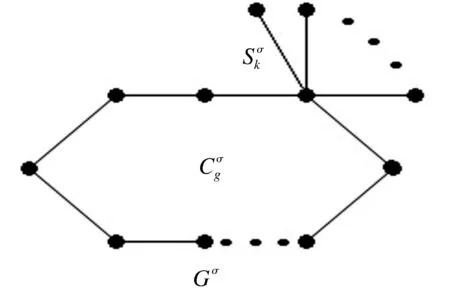
图1 单圈图上的一个Ⅰ- 型悬挂星Figure 1 An unicyclic graph with a Ⅰ- type pendant star

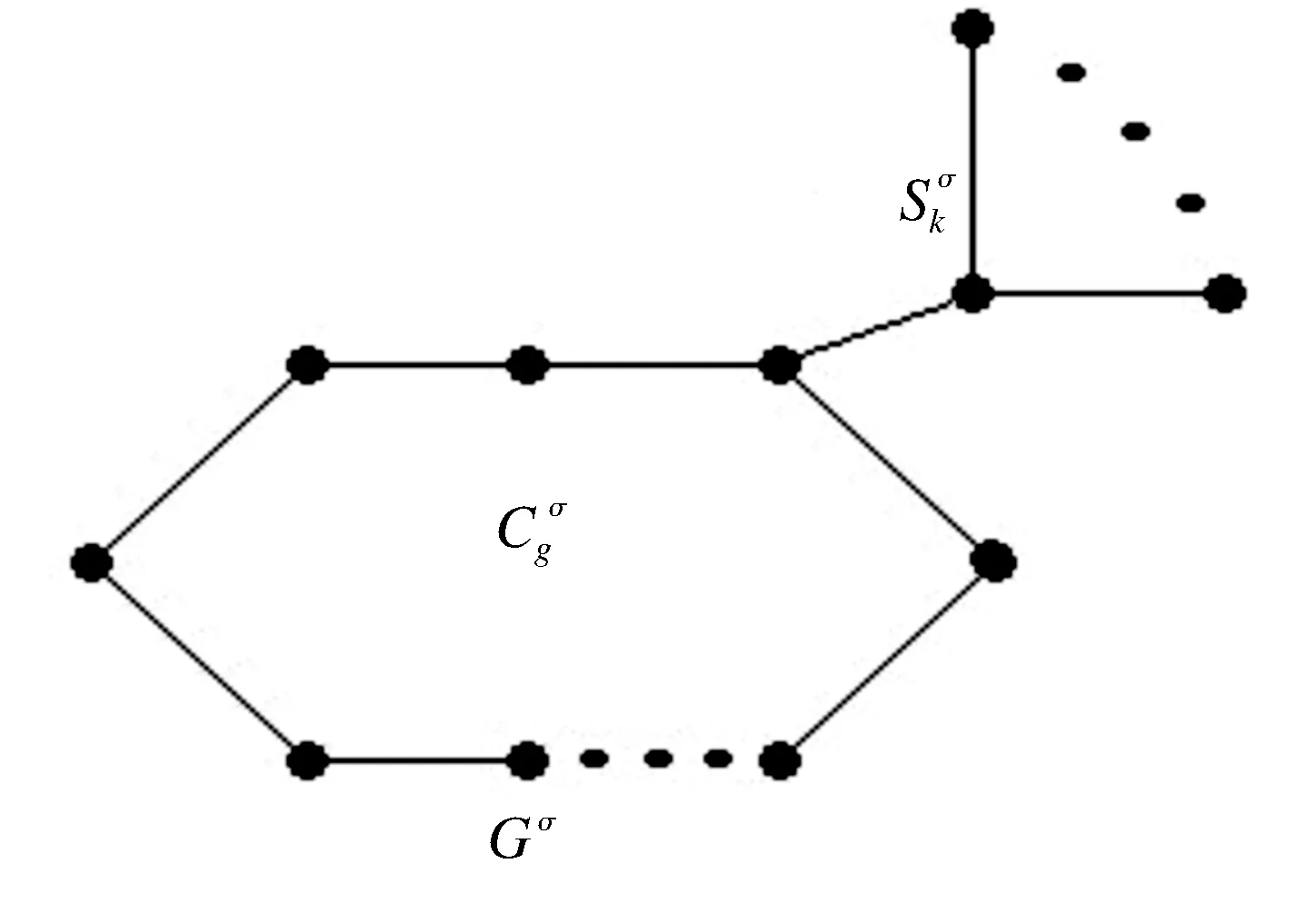
图2 单圈图上的一个Ⅱ- 型悬挂星Figure 2 An unicyclic graph with a Ⅱ- type pendant star

对简单图G, 图G的秩r(G)与结构参数的关系是近年来图谱理论的热点问题之一.其中, Wong[1]等首次发现了r(G)与其直径d(G)的关系, 即对任意图G,总有r(G)≥d(G).他们还刻画了r(G)=d(G)时的所有图.Ma[2]等紧接着刻画了r(G)=d(G)-1的所有图.S.Gong[3]等研究了带切点的图的零度.Zhou[4]等得到了秩与围长g(G)的关系, 即r(G)≥g(G)-2, 并刻画了满足r(G)=g(G)-2,r(G)=g(G)-1或r(G)=g(G)的所有图.针对定向图, Adiga[5]等描述了有向图的斜能量知识.Y.Guo[6]等研究了具有小围长平面图的强边染色问题.Luo[11]刻画了|sr(Gσ)-r(G) |=2d(G)以及sr(Gσ)/r(G)=1+d(G) )的所有图.Wong[12]等发现了定向图的sr(Gσ)及其底图的r(G)的关系, 即sr(Gσ)-r(G)≤2d(G), 并刻画了sr(Gσ)-r(G)=2d(G)的所有图.郑连江[10]等运用奇异值不等式，得到了有向图斜能量和去边后的有向子图斜能量之间的若干性质.本文刻画了斜秩等于围长的定向单圈图, 即针对定向单圈图给出了sr(Gσ)=g(G)的充要条件.

1 相关引理

引理1[7-10]

1) 设Hσ是图Gσ的一个导出子图, 则sr(Gσ)≥sr(Hσ).

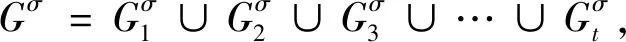
3) 设Gσ是一个定向图, 则sr(Gσ)=0当且仅当Gσ是一个无边图(空图).

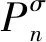
引理4[9-10,14-15]设Gσ是一个定向图,v是Gσ的悬挂顶点且u是悬挂顶点v的唯一邻点, 则

sr(Gσ)=sr(Gσ-v-u)+2.

2 主要结果

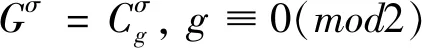
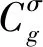
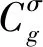
充分性证明: 依据Gσ满足以上三个条件之一, 我们分别讨论以下情形.

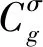
若k=1, 圈上的一个顶点vi1有Ⅰ- 型悬挂星.删除该悬挂星后得到一条定向路, 记为Pσ.根据引理3和引理4, 可得sr(Gσ)=sr(Pσ)+2,sr(Pσ)=g-2, 从而sr(Gσ)=g.

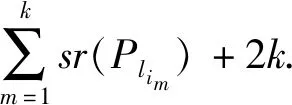
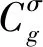
情形1: 存在顶点x使得d(x,Cg)≥3, 此时必存在顶点x,y,u,v, 使得xyuv是G中Cg上顶点v的一条悬挂路.设Hσ是Gσ的由V(Cg)∪{u,x,y}导出的子图.删除Hσ中顶点x,y,u,v得到一条定向路, 记为Pσ.则根据引理1, 引理3与引理4分别有sr(Gσ)≥sr(Hσ),sr(Hσ)≥sr(Pσ)+4以及sr(Pσ)≥g-2.从而sr(Gσ)≥g+2, 此时与题意矛盾, 从而此情形不成立.

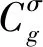
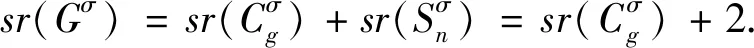
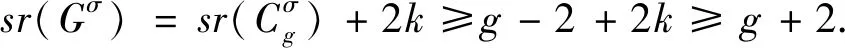
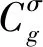
如果k=1, 删除该悬挂星后得到一条定向路, 记为Pσ.根据引理4, 可得sr(Gσ)=sr(Pσ)+2.由于sr(Gσ)=g, 则sr(Pσ)=g-2.因此g是偶数, 即g≡0 (mod2).