受媒体报道影响的离散传染病模型的分析

张雪妮，刘俊利

(西安工程大学 理学院， 西安 710048)

传染病的预防和控制是人们关注的一个重要问题．当出现一种新疾病时，个人必须认识到这种传染病的传染性、毒性和致死率。媒体对疫情的报道，可以让公众了解疫情的风险程度，并鼓励公众采取预防措施．人们提出了许多数学模型来研究媒体报道对传染病的影响[1-3]．模型中通常有两种方法将媒体报道的信息加入到传染病模型中：1)在疾病的传播率中考虑媒体报道的影响[4]；2)通过引入独立仓室来表示媒体报道的信息量的变化[5-6]．事实表明媒体报道在传染病传播过程中起着非常重要的作用，2011年Tchuenche等[7]研究了媒体报道在H1N1传播中的作用．最近，Chang[8]和Yan等[9]研究了媒体报道对新型冠状病毒肺炎(COVID-19)传播的影响．

不少学者对连续的传染病模型进行了研究，但对于许多实际需求，往往需要对连续模型进行离散化.对连续模型进行离散化的方法有很多，如：欧拉法、Runge-Kutta法、非标准有限差分法．目前，离散传染病模型的研究包括阈值和基本再生数的计算[10]，疾病的持久性和灭绝性[11-12]，分支和混沌现象[13-14]，无病平衡点和地方病平衡点的局部稳定性和全局稳定性[15-17]等． 2015年，Liu等[16]使用欧拉向前差分法和非标准有限差分法离散了连续的SIR和SEIR模型，证明了离散模型地方病平衡点的全局稳定性，并对比了两种方法的离散结果．2016年，Teng等[17]利用欧拉向后差分法离散了一类具有非线性发生率的SIRS模型，证明了解的正性及有界性，并构造Lyapunov函数研究了离散模型平衡点的全局稳定性．与连续模型相比，离散模型可以呈现更复杂的动力学性态．

本文先考虑了一个连续的模型，引入独立仓室来研究媒体报道对疾病的影响，通过欧拉向后差分法得到了该连续模型所对应的离散模型，利用线性化方法分析离散模型平衡点的局部稳定性，并构造Lyapunov函数讨论平衡点的全局稳定性．

1 模型的建立

考虑如下连续模型：

(1)

其中：S(t)，Sa(t)，I(t)分别代表t时刻无意识易感者，有意识易感者和感染者的数量，M(t)代表t时刻媒体的播报量．A表示人口的常数输入率，β1表示易感人群的传染率，β2表示无意识人群受媒体播报影响的疾病意识获取率，d表示人口的自然死亡率，δ表示有意识人群疾病意识的失去率，η表示媒体播报的数量受疾病影响的生成率，θ表示疾病意识衰减率.

本文的目的是研究模型(1)所对应的离散化模型．利用欧拉向后差分法得到模型(1)对应的离散化模型：

(2)

其中：S(n)，Sa(n)，I(n)分别为第n个时间步长无意识易感者，有意识易感者和感染者的数量，M(n)表示第n个时间步长的媒体的播报量，h>0表示步长，其他参数与连续模型(1)中的含义一样．

根据模型(2)的生物学意义,假定所研究模型的解满足如下的初始条件:

S(0)>0,Sa(0)>0,I(0)>0,M(0)>0.

(3)

下面给出模型(2)解的非负性和有界性．

定理1 设(S(n),Sa(n),I(n),M(n))是模型(2)满足初始条件(3)的解，则对任意的n>0，(S(n),Sa(n),I(n),M(n))都是正的，且最终有界．

证明：首先证明解的正性. 模型(2)可以写为：

(4)

令a1=1+h(δ+d)，将式(4)的第二个方程带入第一个方程中得：

S(n+1)=

(5)

将式(4)的第四个方程带入式(5)中得：

(6)

将式(6)带入式(4)的第三个方程中得：

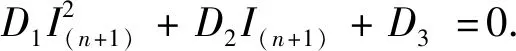
当n=1时，同理可证I(2)>0，进而S(2)>0，M(2)>0，Sa(2)>0．最后使用归纳法得：对∀n>0,(S(n),Sa(n),I(n),M(n))都是正的．

下证解是最终有界的．设N(n)=S(n)+Sa(n)+I(n)，将模型(2)的前三个方程相加得：N(n+1)=N(n)+hA-hdN(n+1)，则有：

2 平衡点的局部稳定性分析

模型(2)的基本再生数和平衡点都与模型(1)相同．这一节将研究模型(2)平衡点的局部稳定性．

证明：模型(2)在无病平衡点E0处的线性化系统为：

(7)

将式(7)写为矩阵形式：

其中：

C=

矩阵C的四个特征值分别为：

λ1=1+hd>1,λ2=1+hd+hδ>1,λ3=1+hθ>1,λ4=1+hd(1-R0).

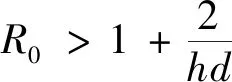
下面给出模型(2)地方病平衡点的局部稳定性结论．

证明：模型(2)在地方病平衡点E*处的线性化系统为：

(8)

将式(8)写为矩阵形式

其中：

如果-D的所有特征值λi,i=1,2,3,4，满足|λi|>1．则D-1的所有特征值σi,i=1,2,3,4，满足|σi|<1．下证-D的所有特征值满足|λi|>1,(i=1,2,3,4)．

r4+B1r3+B2r2+B3r+B4=0

(9)

(d+β1I*)(δ+d)y1+y3y5>0,

θ(δ+d)(d+β1I*)(B1B2-B3)+

(θ+y1)2dy0-θ2y1y4>θy3(B1B2-B3-θ2y1)-

θ2y1y4>θy1y3(δ+d)(d+β1I*)-θ2y1y4>

θdy1y4-θ2y1y4,

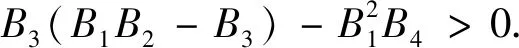
3 平衡点的全局稳定性分析

ΔL(n)=L(n+1)-L(n)=I(n+1)-I(n)=

h(β1S(n+1)I(n+1)-dIn+1)≤

(10)

当R0>1时，模型(10)的地方病平衡点为E*(S*,I*,M*)，其中：

定理5 当R0>1时，若以下条件成立：

(11)

则模型(10)的地方病平衡点E*(S*，I*，M*)全局渐近稳定．

这里函数g(x)=x-1-lnx≥0，∀x∈R+，g(x)=0当且仅当x=1．因此

ΔV1(n)=V1(S(n+1))-V1(S(n))=

ΔV2(n)=V2(I(n+1))-V2(I(n))=

ΔV3(n)=V3(Mn+1)-V3(M(n))=

又因为

由式(11)知

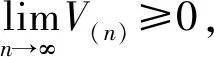
4 数值模拟

取步长h=1.25，初值为S(0)=0.3，Sa(0)=0.3，I(0)=0.5，M(0)=0.3，取参数值为：d=0.01，δ=0.2，θ=0.06，η=0.01，A=0.002，β1=0.009，β2=0.25，此时得R0=0.18<1，在这组参数下无病平衡点(0.2,0,0,0)全局渐近稳定，如图1所示．

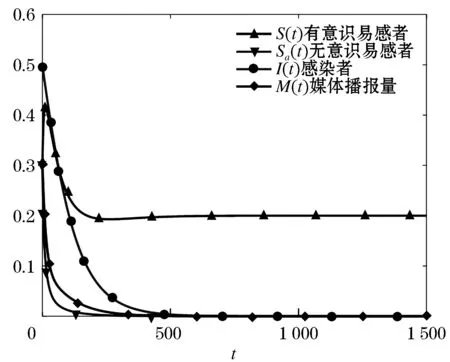
图1 模型(2)无病平衡点的全局稳定性Figure 1 The global stability of the disease free equilibrium of model (2)

若取d=0.01，δ=0.1，θ=0.04，η=0.08，A=0.02，β1=0.02，β2=0.25，此时R0=4>1，在这组参数下地方病平衡点(0.5,1.041 7, 0.458 3,0.916 7)全局渐近稳定，如图2所示．

图2 模型(2)地方病平衡点的全局稳定性Figure 2 The global stability of the endemic equilibrium of model (2)

5 结 语

本文研究了受媒体报道影响的离散传染病模型，得到了模型(2)解的正性和有界性．模型(2)总存在一个无病平衡点，当基本再生数大于1时，除无病平衡点外模型(2)还存在一个地方病平衡点．理论分析表明，当基本再生数R0<1时，模型(2)的无病平衡点全局渐近稳定；当R0>1时，在一定条件下模型(2)的地方病平衡点是局部渐近稳定的，另外当δ=0时，若(11)式成立则模型(10)的地方病平衡点全局渐近稳定．数值仿真证明了理论结果的正确性．