通过“底图”突破立体几何的建系难点

常艳 龙宇

[摘   要]学生常常通过向量解决立体几何问题，而如何选择建系的原点是一大难点.通过对“底图”的分析，能为学生建系提供思考的方向.

[关键词]底图;建系;立体几何

[中图分类号]    G633.6        [文献标识码]    A        [文章编号]    1674-6058（2019）23-0024-02

解决立体几何问题有几何法和空间向量法.几何法涉及辅助线的添加及空间关系的理解.与几何法相比，向量法的思维量小，所以向量法成为更多学生的首选.运用向量法的一大难点在于坐标系的建立.本文介绍一种以“底图”为思考出发点的建系策略，供读者参考.这里说的“底图”是指立体图形中的底面图形.

一、题目

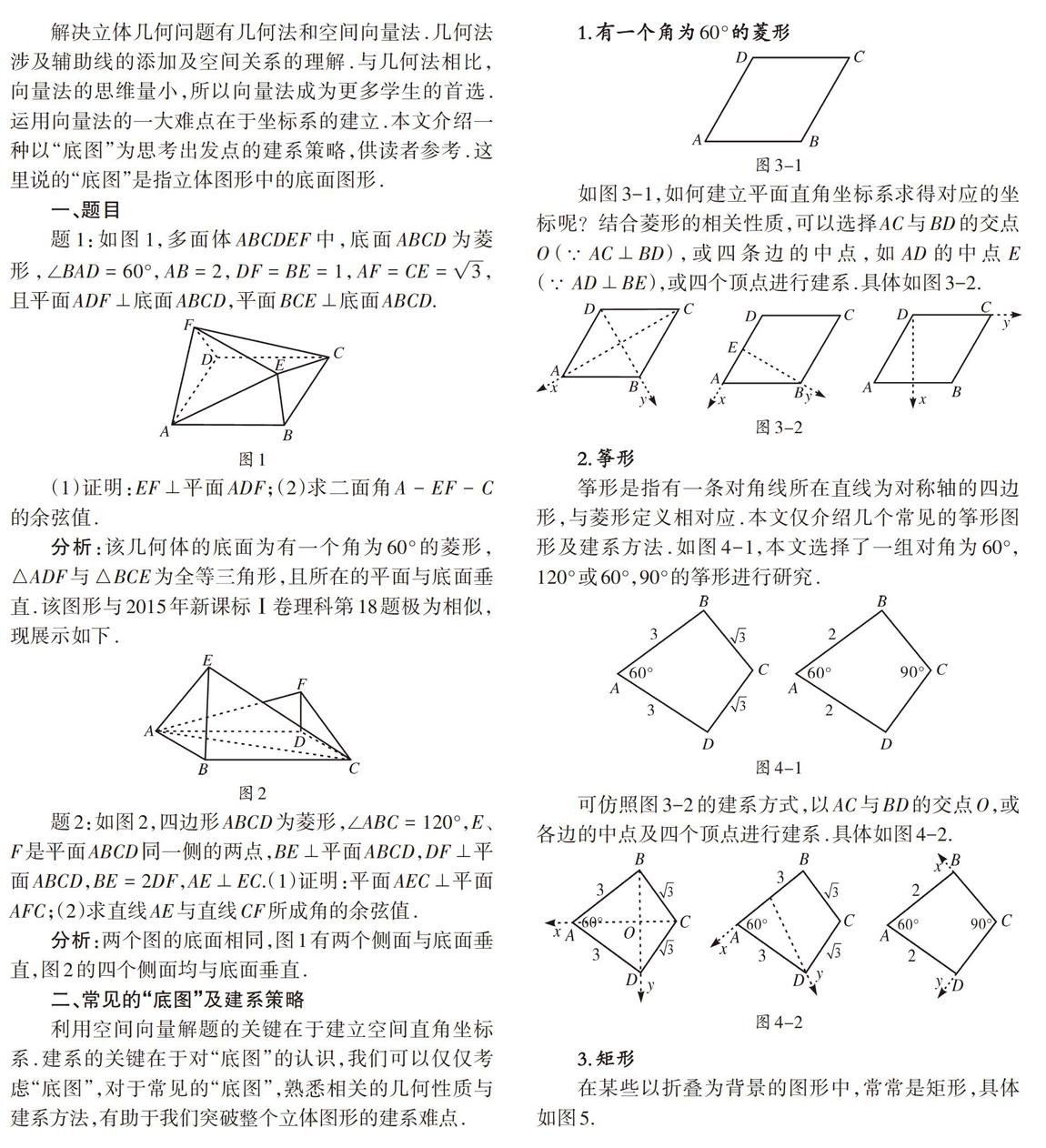
题1：如图1，多面体[ABCDEF]中，底面[ABCD]为菱形，[∠BAD=60°]，[AB=2]，[DF=BE=1]，[AF=CE=3]，且平面[ADF⊥]底面[ABCD]，平面[BCE⊥]底面[ABCD].

（1）证明：[EF⊥]平面[ADF];（2）求二面角[A-EF-C]的余弦值.

分析：该几何体的底面为有一个角为[60°]的菱形，[△ADF]与[△BCE]为全等三角形，且所在的平面与底面垂直.该图形与2015年新课标Ⅰ卷理科第18题极为相似，现展示如下.

题2：如图2，四边形[ABCD]为菱形，[∠ABC=120°]，[E]、[F]是平面[ABCD]同一侧的两点，[BE⊥]平面[ABCD]，[DF⊥]平面[ABCD]，[BE=2DF]，[AE⊥EC].（1）证明：平面[AEC⊥]平面[AFC];（2）求直线[AE]与直线[CF]所成角的余弦值.

分析：兩个图的底面相同，图1有两个侧面与底面垂直，图2的四个侧面均与底面垂直.

二、常见的“底图”及建系策略

利用空间向量解题的关键在于建立空间直角坐标系.建系的关键在于对“底图”的认识，我们可以仅仅考虑“底图”，对于常见的“底图”，熟悉相关的几何性质与建系方法，有助于我们突破整个立体图形的建系难点.

1.有一个角为[60°]的菱形

如图3-1，如何建立平面直角坐标系求得对应的坐标呢？结合菱形的相关性质，可以选择[AC]与[BD]的交点[O]（[∵AC⊥BD]），或四条边的中点，如[AD]的中点[E]（[∵AD⊥BE]），或四个顶点进行建系.具体如图3-2.

2.筝形

筝形是指有一条对角线所在直线为对称轴的四边形，与菱形定义相对应.本文仅介绍几个常见的筝形图形及建系方法.如图4-1，本文选择了一组对角为[60°]，[120°]或[60°]，[90°]的筝形进行研究.

可仿照图3-2的建系方式，以[AC]与[BD]的交点[O]，或各边的中点及四个顶点进行建系.具体如图4-2.

3.矩形

在某些以折叠为背景的图形中，常常是矩形，具体如图5.

利用三角形相似或向量等方法可容易证明[AE⊥BD].即可以选择以[AE与BD]的交点[O]进行建系.

三、解法呈现

解法一：有了上面的“底图”分析作为基础，学生就可以有效地解决题1的建系问题.

如图6-1建系，以[AD]的中点[O]为原点，建立空间直角坐标系，也可选择[AC]与[BD]的中点或[A，B，C，D]进行建系，得到各个点的空间坐标.

[O（0，0，0）]，[A（1，0，0）]，[B（0，3，0）]，[C（-2，3，0）]，[D（-1，0，0）]，[E-12，3，32]，[F-12，0，32].关于点[E，F]的坐标，可根据其所在平面计算.结合上面的坐标即可解决所有问题.

对于题2，可如图6-2建系，以[AC与BD]的交点[G]建立空间直角坐标系.对应的各点坐标如下：

设菱形[ABCD]的棱长为[2]，则有[G（0，0，0）]，[A（0，-3，0）] ，[B（1，0，0）] ，[C（0，3，0）] ，[D（-1，0，0）]，[E（1，0，2）]，[F-1，0，22 ].

解法二：题1中，两个侧面[△ADF]和[△BCE]为全等的直角三角形.结合上文中的“折叠”模型，将图1中的[△ADF]和[△BCE]分别绕[AD，BC]旋转即可获得一个完整的“矩形”.具体如图7-1.

设[AD]与[EF]的交点为[O]，根据图5，可在点[O]处建系，具体如图7-2.

对应的各点的坐标如下：[O（0，0，0）]，[A43，0，0]，[B23，3，0]，[C-43，3，0]，[D-23，0，0]，[E0，3，32]，[F0，0，32] .

根据以上的坐标即可获得问题的解.

两种解答模式的基本思路一致，均是以“底图”进行思考.

除了上面的几种“底图”外，常见的“底图”还有三角形、梯形等.教师在平时的教学中，应让学生学会分析“底图”，将建系的难点从空间维度降低到平面维度.对此，平面图形的几何性质，特别是垂直关系就显得尤为重要，在平时的训练中要注意对该类性质的积累.

（责任编辑 黄桂坚）