基于空间基函数优化组合的微波加热温度分布数值求解

杨 彪 马红涛杜 婉刘 承高 皓

(1.昆明理工大学信息工程与自动化学院,云南昆明 650500;2.昆明理工大学云南省人工智能重点实验室,云南昆明 650500;3.昆明理工大学非常规冶金教育部重点实验室,云南昆明 650093)

1 引言

近些年来随着微波加热技术的成熟,微波加热在工业方面取得了广泛的应用.与传统的加热方式相比微波加热具有高效率,清洁无污染的优点.用于食品加工、木材干燥以及化工产业等[1-3].微波加热与传统热工过程有很大不同,传统加热中热量从媒质外部通过对流、传导、热辐射进入媒质内部,而微波加热则是通过电磁场使得被加热媒质内部极性分子在短时间内快速相互作用从而产生大量的热.微波加热在加热效率快速高效的同时也伴随着加热温度分布不均匀的缺点,热点和冷点的出现会导致局部过热的现象,当局部温度超过材料临界温度时就会产生热失控[4].热失控现象是阻碍微波加热工业应用发展的重大阻碍.研究求解微波加热过程中媒质的全局温度分布是预防和解决热失控现象的首要问题.

微波加热温度模型由热传递方程、边界条件、初始温度条件组成,热传递方程可由一类典型的抛物线型偏微分方程(partial differential equations,PDE)表示,其具有强烈的时空耦合特性及时间与空间无限维的特点,并且热传递模型的非齐次耗散功率项的存在导致微波加热温度模型具有强烈的非线性特征,再加上热动力学场非齐次边界条件和初始温度的影响,利用解析方法获得全局温度分布的表达式几乎是不可能的,因此不少学者对微波加热过程中的温度分布求解提出了多种数值计算方法.Yang等[5]通过COMSOL建立了多馈微波装置流体加热的三维有限元数值模型,模拟了不同功率、初始温度等参数对加热温度的影响,最终选择出最佳加热管半径.Oliveira等[6]利用有限元法与分析技术相结合解决了加载陶瓷样品的单模填充器内部热电磁问题.Ma[7]等利用时域有限差分法(finite difference time domain method,FDTD)描述微波加热德拜物质的温度分布.此外还有许多数值方法,比如传输线矩阵法(transmission line matrix,TLM)、矩量法(method of moments,MOM)、有限体积法(finite volume method,FVM)等[8-10].虽然上述数值方法能有效的解决微波加热过程中的温度分布问题,但是在计算过程中计算速度、精度和实时性很难取得良好的平衡,因此需寻求一种新的求解微波加热温度分布的方法.

Zhong等[11]利用辅助函数提出一个中间模型,将PDE温度模型的非齐次Dirichlet边界条件转化为齐次Dirichlet边界条件,便于求得PDE模型空间微分算子的特征值与特征函数,并将特征函数作为全局空间基函数[12],以空间基函数和其对应时间系数的级数和的形式将PDE模型进行时空分离,结合伽辽金权重残差法(Galerkin weighted residual method,GWRM)[13]和谱方法成功将无限维PDE模型转化为近似有限维ODE模型.并将模型的数值仿真结果与传统数值方法求解结果进行对比验证了该近似模型的有效性.虽然该方法将无限维模型近似为有限维模型,大大减小了模型计算的复杂度,但是在该方法中有限维ODE模型阶数的选取有较大的主观性,并且根据理论分析判断模型阶数的选取对全局温度分布的求解有较大的影响,当阶数取较大数值时,有限维ODE温度模型维数较高能保证全局温度分布求解的精度但会使计算时间过长实时性降低.当阶数取较小数值时,实时性增强但精度会降低.寻找一个合适的方法使得ODE温度模型温度分布求解的计算速度和计算精度达到一个更好的平衡是本文的主要目的.

受到Zhong有限维微波加热ODE模型的启发,本文在第3节中通过寻找一个最优的空间基函数转换矩阵将其选取的全局空间基函数进行线性组合[14],转换矩阵的取值可通过最小化误差函数近似得到,误差函数表示为优化组合后的空间基函数对应的ODE模型与初始空间基函数对应的ODE模型之间预测输出的差值.通过优化组合后的空间基函数将有限维ODE温度模型进一步降维.第4节中,本文首先求解了初始高维ODE模型不同阶数取值下的温度分布与求解时间,分析了阶数取值的不同对温度分布求解的影响,并通过不同模型阶数下某些点处温度的趋势走向选取了合适的高维ODE模型阶数求得近似标准温度分布.其次,同样的将进一步降维后的低维ODE模型在不同阶数取值的情况下进行数值仿真求解,得到其温度分布和计算时间,分别将初始高维ODE模型不同阶数取值下的温度分布和低维ODE模型在不同阶数取值下温度分布与近似标准温度分布进行对比.最后,利用有多物理场仿真软件(COMSOL),即有限元方法(finite element method,FEM)再次验证了模型的准确性,充分证明了本文方法的有效性.

2 微波加热温度模型

2.1 无限维微波加热PDE温度模型

在微波加热过程中,电磁场随时间空间变化的规律可由Maxwell方程表示,麦克斯韦方程组根据电磁理论,变化的电场和变化的磁场相互激发,相互联系形成统一的电磁场.Maxwell 方程组可写成如下形式[15]:

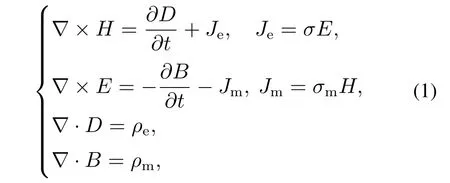
其中:Je,Jm,ρe,ρm分别表示电流密度、磁流密度、电荷密度和磁荷密度;σm是磁电阻率(Ω/m)对应磁场的损耗.在无源媒质中ρe=0和ρm=0,在无电或无磁损耗的媒质中可令σ或σm等于0.H表示磁场强度,E表示电场强度,B表示磁感应强度,D表示电位移矢量.

微波加热过程中,被加热媒质中的电磁场计算可由Helmholtz方程[16]表示:

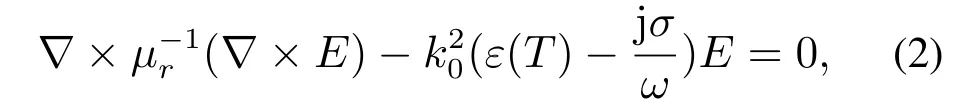
其中:k0=表示媒质的相对磁导率,ε(T)表示媒质的复介电常数,σ表示媒质的电导率,E和ω分别入射电场强度和入射电磁波角频率,k0表示自由空间的波数,ε0=8.854×10−14F/cm,µ0=4π×10−7H/m表示真空磁导率,j表示虚数单位.

在笛卡尔坐标系下,根据热动力学第一定律及傅里叶热传导定律,在一维方向上微波加热媒质过程可由下述含非齐次项的偏微分方程进行描述[17]:

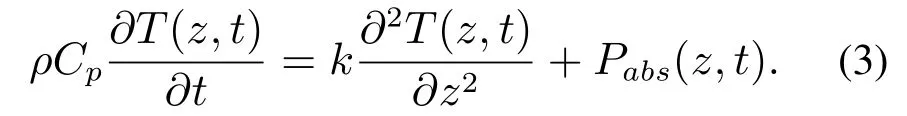
非齐次Dirichlet边界条件:

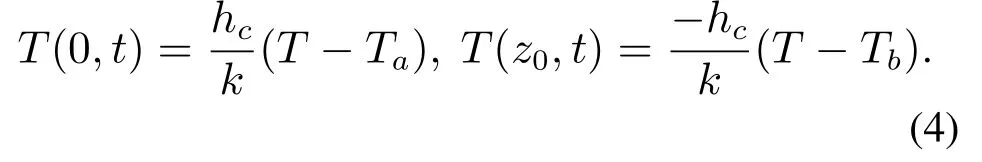
初始温度条件:

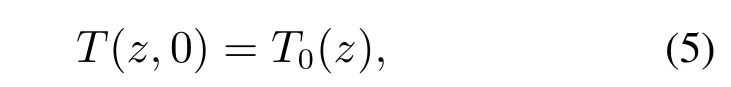
其中:ρ,Cp,k分别表示加热媒质的密度,比热容和导热系数.hc表示热传系数,Ta,Tb表示环境温度.Pabs表示耗散功率,微波功率的计算可采用朗伯(Lambert)定律,朗伯定律[18]以指数衰减的形式表示被加热媒质内部微波能量吸收的情形,在对被加热媒质的全局温度分布趋势的研究上在很大程度上降低了电磁场计算的复杂性.Lambert定理所适用的条件为:电磁场垂直入射到媒质表面,介电常数不随温度变化,并且媒质长度是无限的.然而上述使用条件仅仅是在理想状态下,而在实际应用中,若媒质的长度大于或者等于趋肤深度的2倍,就可以忽略透射波和反射波的影响,近似地将耗散功率写成Lambert定理的形式可表示为

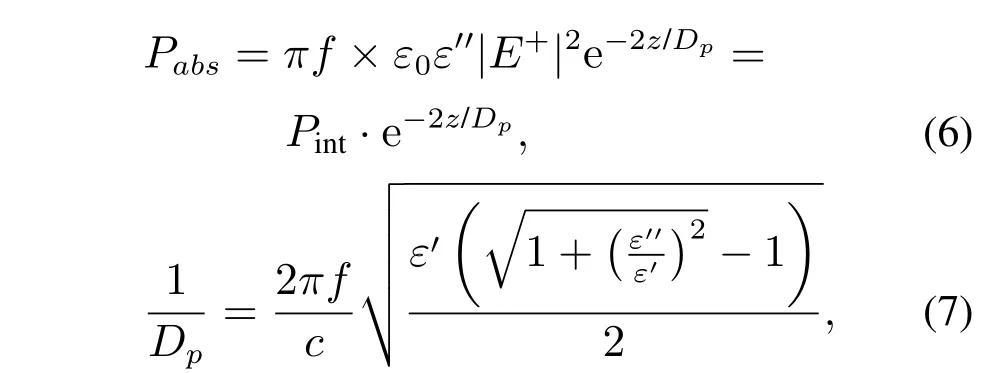
其中:f表示微波频率,ε′′表示相对介电损耗,ε′表示被加热媒质的相对介电系数.E+表示入射电场强度,Pint表示入射功率密度,Dp为趋肤深度,表示入射功率从媒质表面衰减至表面功率值的1/e时的距离,c=3×108m/s为微波在真空环境中的传播速度.

2.2 有限维微波加热ODE温度模型

由于上述PDE模型具有非齐次边界条件的制约,难以获取空间微分算子的特征谱和特征函数,Zhong利用构造辅助函数将模型(3)-(5)等价为如下中间模型[11]:

其中:λi表示特征值,φi(z)表示相对应的特征函数.选择特征函数φi(z)作为空间基函数,式(9)中的时空耦合变量Θ(z,t)可以能展开成一个无限维空间基函数的集合和其对应的时间系数的级数和的形式:

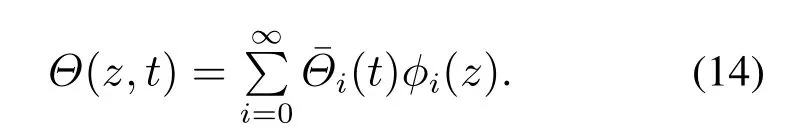
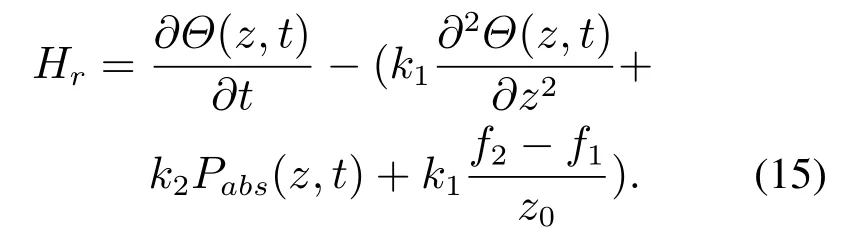
可通过下式进行最小化:

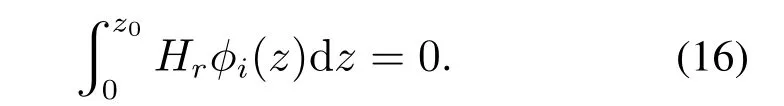
结合式(14),将式(15)带入式(16)可得到时空变量分离的无限维微波加热ODE温度模型:

3 空间基函数变换

空间基函数的选择对于偏微分方程系统的降维十分关键,能极大程度的影响模型的精度.第2节中通过选取空间微分算子的特征函数作为降维的全局基函数,其特征函数是一组无限的光滑的全局正交基函数,非线性偏微分方程动态系统的主要信息存在于有限维特征谱对应的有限维空间基函数中.本小节通过将对上一节中有限维模型的n+1阶空间基函数进行线性组合,得到新的m+1(m ＜n)阶空间基函数,对有限维微波加热ODE温度模型进一步降维,得到阶数更低的有限维模型.

3.1 基函数转换矩阵

定义一个基函数转换矩阵R(n+1)×m+1),矩阵中每个位置的数值都是n+1阶空间基函数进行线性组合,得到新的m+1(m ＜n)阶空间基函数的线性组合系数,可由下式表达:

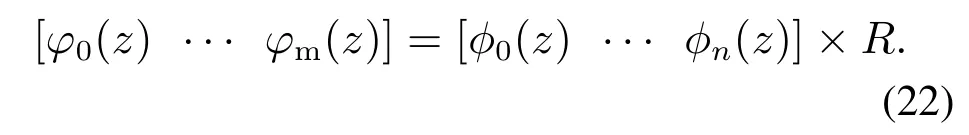
基于m+1阶新空间基函数可得到新的有限维微波加热ODE温度模型,如下:

3.2 基函数转换矩阵的求解

为求解空间基函数的转换矩阵,现给出如下误差函数:

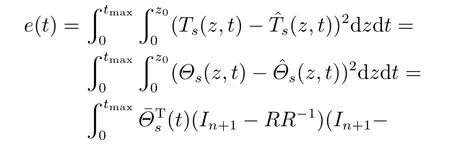
此误差函数表示基于n+1阶空间基函数的ODE温度模型与基于m+1阶空间基函数的ODE温度模型的温度分布的时空积分的平方差,其中tmax表示最大加热时间,z0表示被加热媒质深度,In+1表示n+1阶单位矩阵,从上式可以看出,误差函数只与初始n+1阶空间基函数对应的时间系数相关.

空间基函数转换矩阵可通过最小化误差函数e(t)近似得到,本文对e(t)的最小化采用随机优化的方法来计算求解.粒子群算法[20](particle swarm optimization,PSO)是受自然界中鸟群觅食的启发的一种群体智能优化算法,并且是高精度的随机优化算法.但是传统PSO算法在寻优过程中存在陷入局部最优和早熟收敛的问题.为更准确快速的求得基函数转换矩阵R,本文采用自适应变异粒子群优化算法(adaptive mutation particle swarm optimization,AMPSO)[21],即为粒子群优化算法增加了一个自适应变异机制,即每次算法计算周期,都有一定的概率随机改变某一个个体的数值,从而提高整个粒子群的寻优能力.

在粒子群优化算法的思想中,每个粒子有两个属性,一个是粒子所在的位置,一个是粒子的速度,粒子的运动就是寻找最优解的运动.采用粒子群算法进行本次优化时,每个粒子的位置有(n+1)(m+1)个,其中每个粒子的位置表示为

t表示当前时刻,t −1表示前一时刻,t+1表示后一时刻,ω0为权重系数,c1,c2为学习因子,r1,r2为[0,1]的随机数,T表示粒子每次运动时间.粒子根据自身先前速度以及自身位置与个体最佳位置和群体最优位置的距离更新自身速度,之后运动到新的位置.

基于上述PSO算法,优化求解空间基函数转换矩阵R(n+1)×(m+1)的算法流程如下:

4 仿真分析及验证

4.1 数值仿真及分析

本小节首先通过MATLAB数值仿真验证分析有限维ODE温度模型阶数的取值对微波加热全局温度分布求解的影响,并选取合适的阶数的模型将其温度分布作为近似标准温度分布.接着将ODE温度模型(23)-(25)与模型(19)-(21)在计算速度和温度分布误差方面进行比较,证明了基于m+1阶空间基函数对应的模型的有效性.最后利用FEM验证了m+1阶空间基函数对应的模型的准确性.因为去离子水具有热力学参数随温度变化很小的特性,为更方便的表示本文模型的有效性,假设离子水的热力学参数均不随温度发生变化,介电系数视作恒定,其相应热力学参数如表1所示.假设被加热去离子水的长度大于其2倍的趋肤深度并充满长波导,其加热的示意图如图1所示.

表1 去离子水恒定热力学参数Table 1 Constant thermodynamic parameters of deionized water

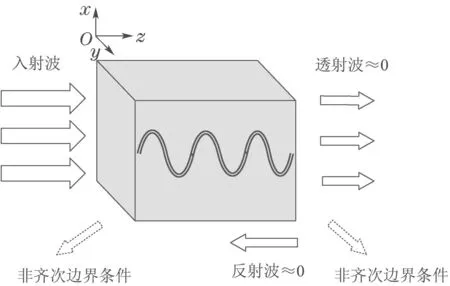
图1 长波导中加热去离子水示意图Fig.1 Schematic diagram of heated deionized water column in long waveguide

当微波频率为2.45 GHz,非齐次边界条件f1=1°C/cm,f2=−1°C/cm,初始温度为20°C,入射功率密度为20 W/cm2,加热时间tmax=10 s,加热物料深度z0=10 cm时,分别求取n=50,n=47,n=45,n=43,n=23,n=3时有限维ODE温度模型的温度分布,其结果如图2(a)-(f)所示.通过对比可以看出模型阶数选取对微波加热全局温度分布求解有很大的影响,选取阶数越大,计算时间增加温度分布越精确,相反,计算时间减少温度分布的误差越明显.

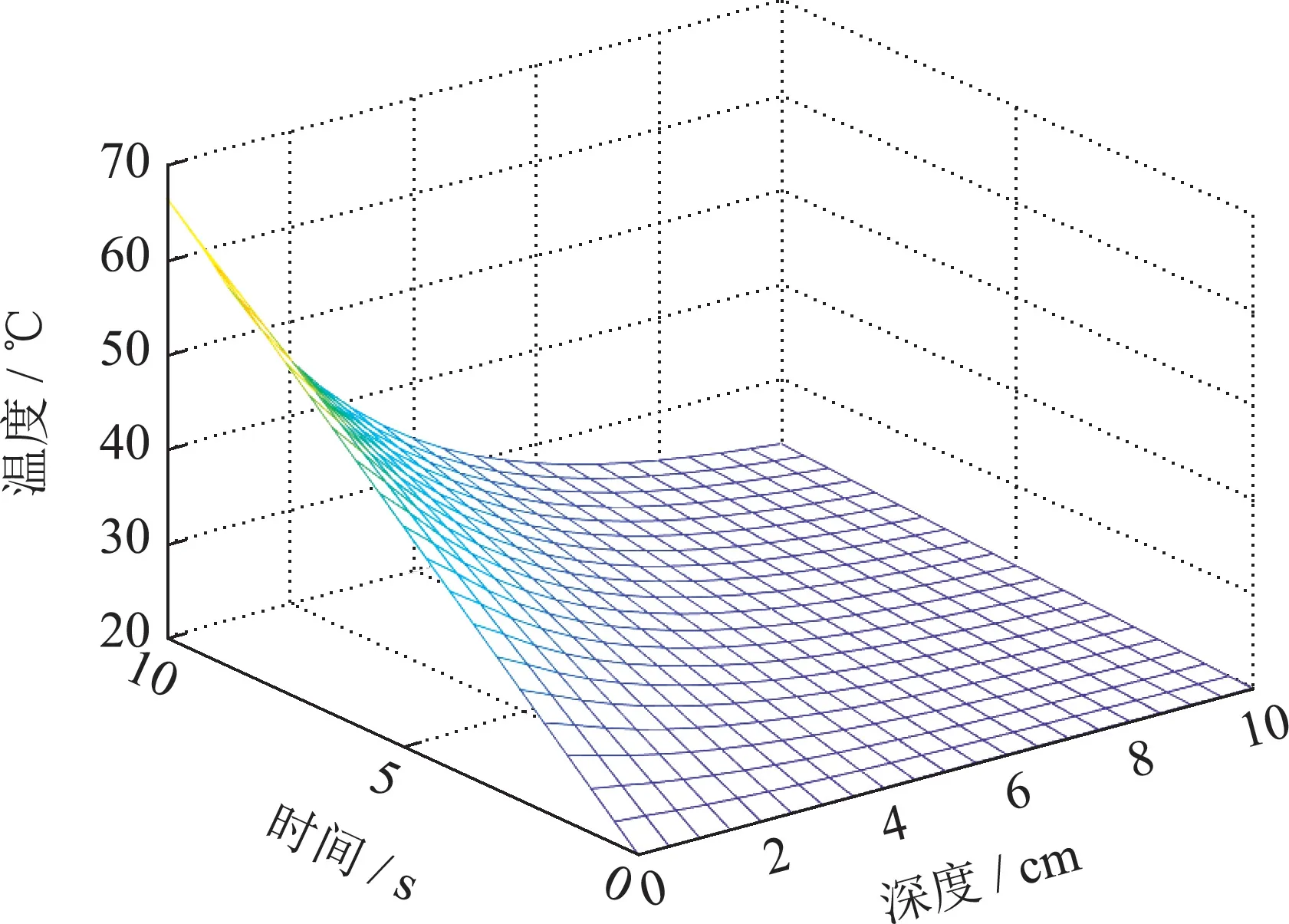
图2(a) n=50温度分布Fig.2(a) n=50 temperature distribution

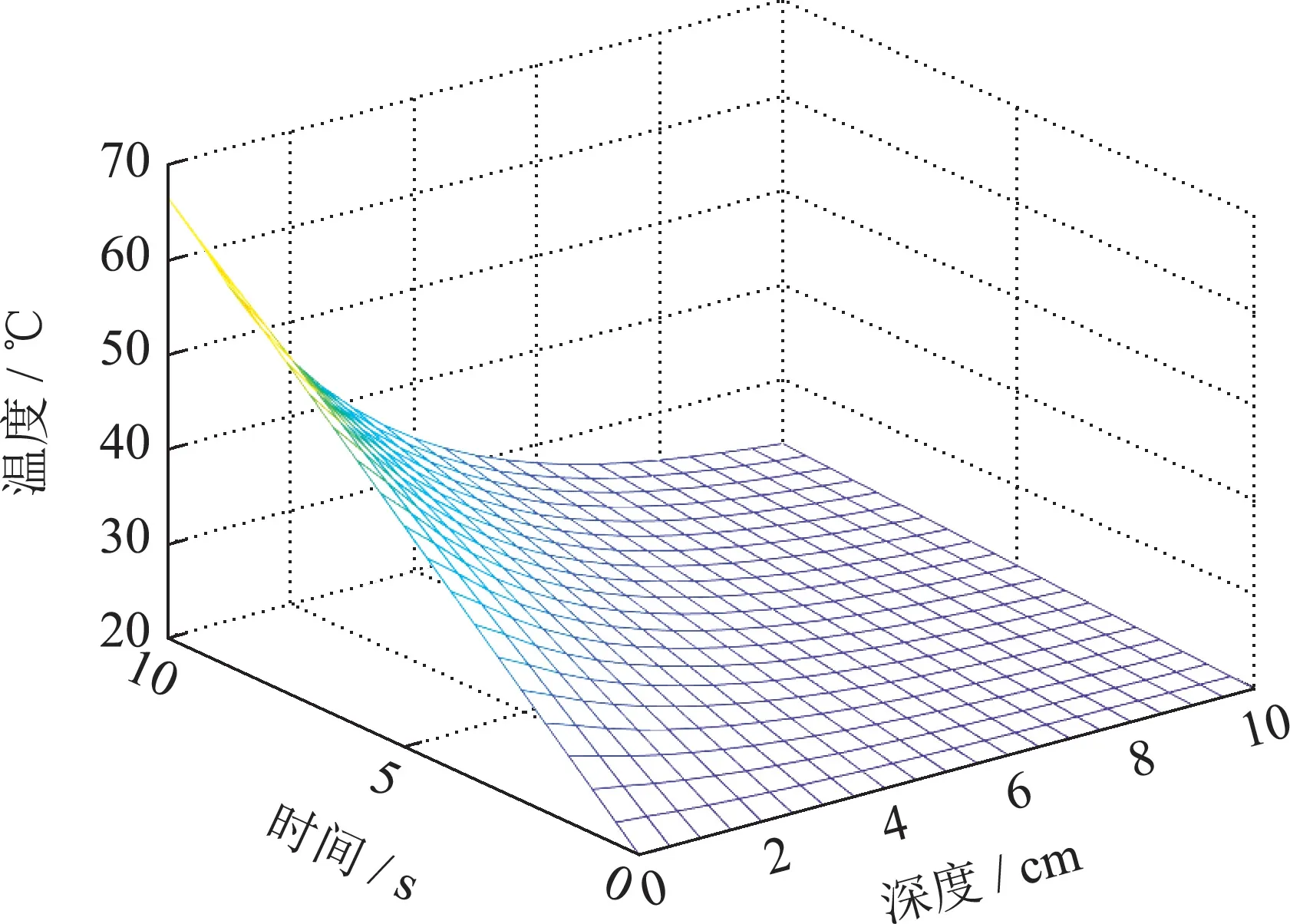
图2(b) n=47温度分布Fig.2(b) n=47 temperature distribution

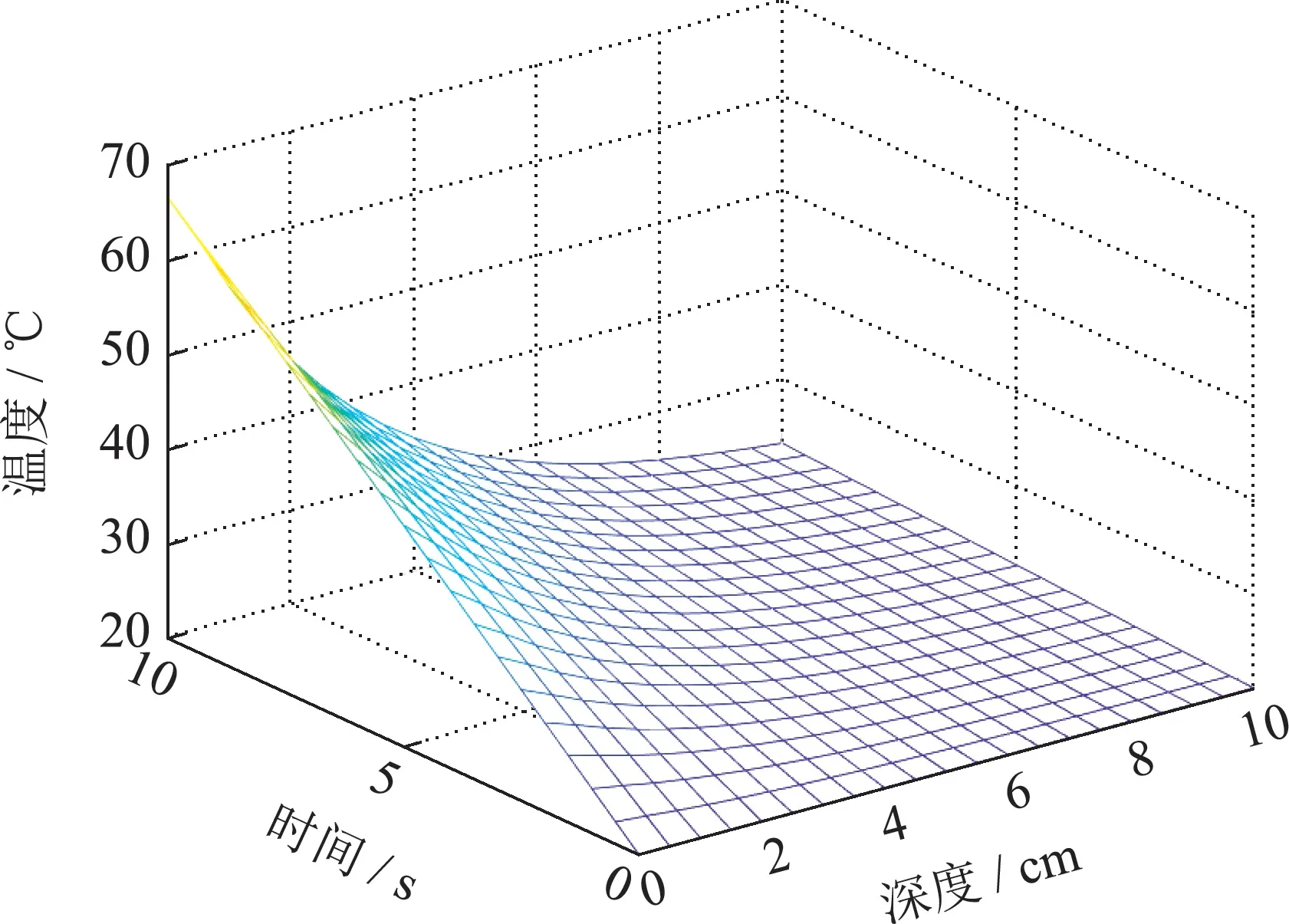
图2(c) n=45温度分布Fig.2(c) n=45 temperature distribution

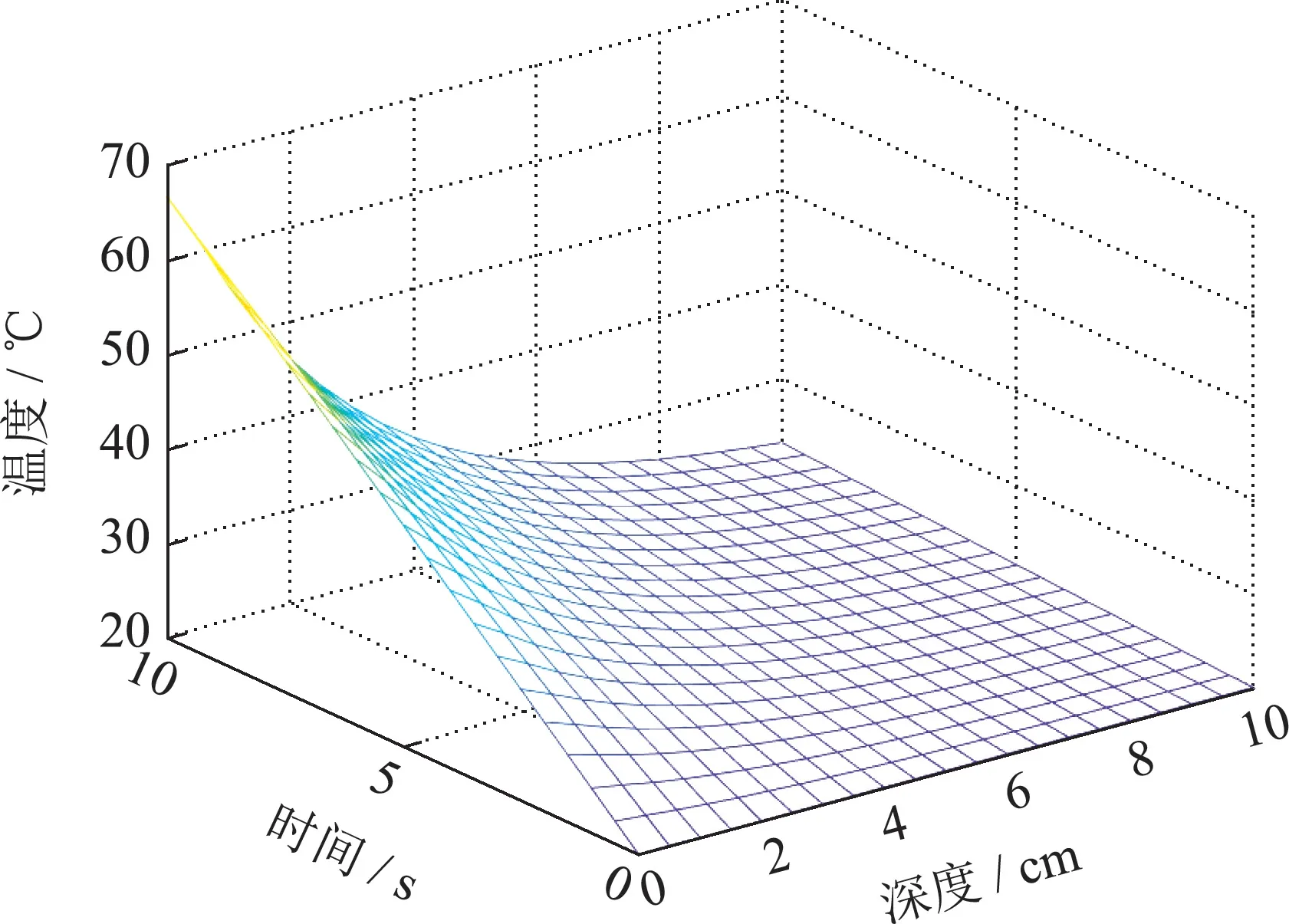
图2(d) n=43温度分布Fig.2(d) n=43 temperature distribution

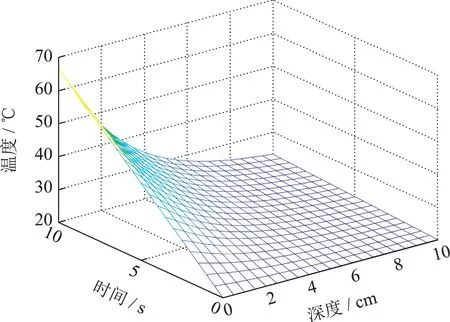
图2(e) n=23温度分布Fig.2(e) n=23 temperature distribution

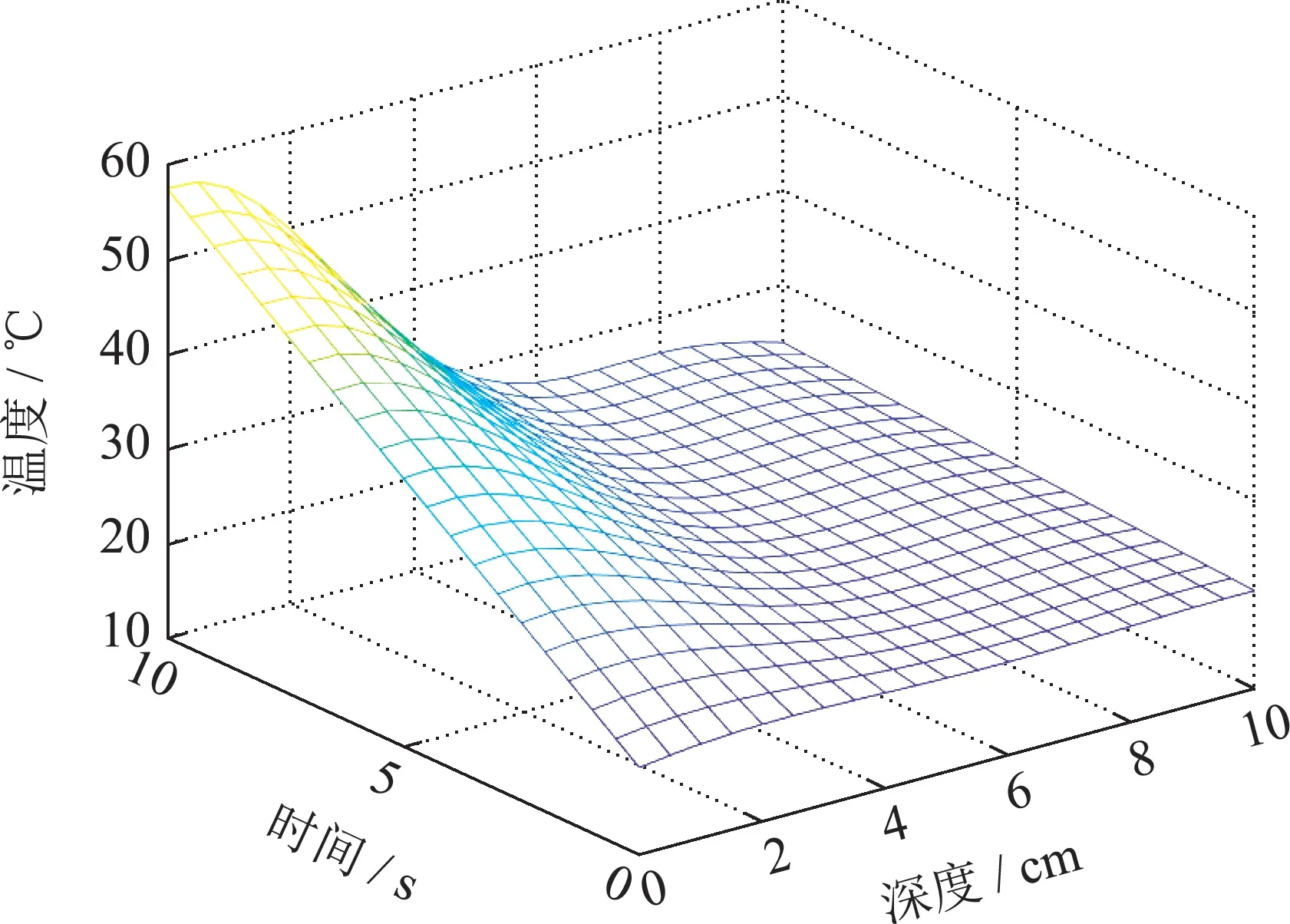
图2(f) n=3温度分布Fig.2(f) n=3 temperature distribution

从图2(a)中可以明显看到在微波加热过程中馈口位置吸收大量微波能量,迅速升温,随着介质深度的增加微波功率密度呈指数型衰减,升温速度也随之改变,其温度变化符合Lambert定律的温度变化走向,并与Zhong进行对比保证了基于初始n+1阶空间基函数对应的ODE温度模型的有效性.取不同模型阶数下t=4 s,z=1.5 cm;t=5 s,z=2 cm;t=6 s,z=1 cm 三点处的温度趋势如图3(a)-(c)所示.

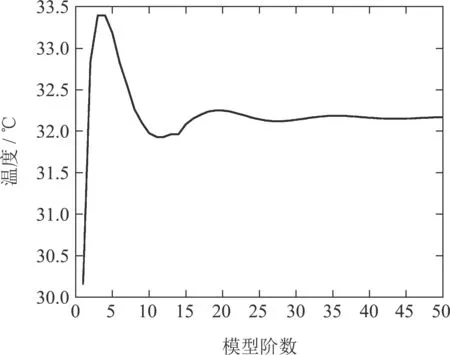
图3(a) 不同阶数下t=4 s,z=1.5 cm处温度趋势Fig.3(a) Temperature trend at t=4 s,z=1.5 cm under different orders

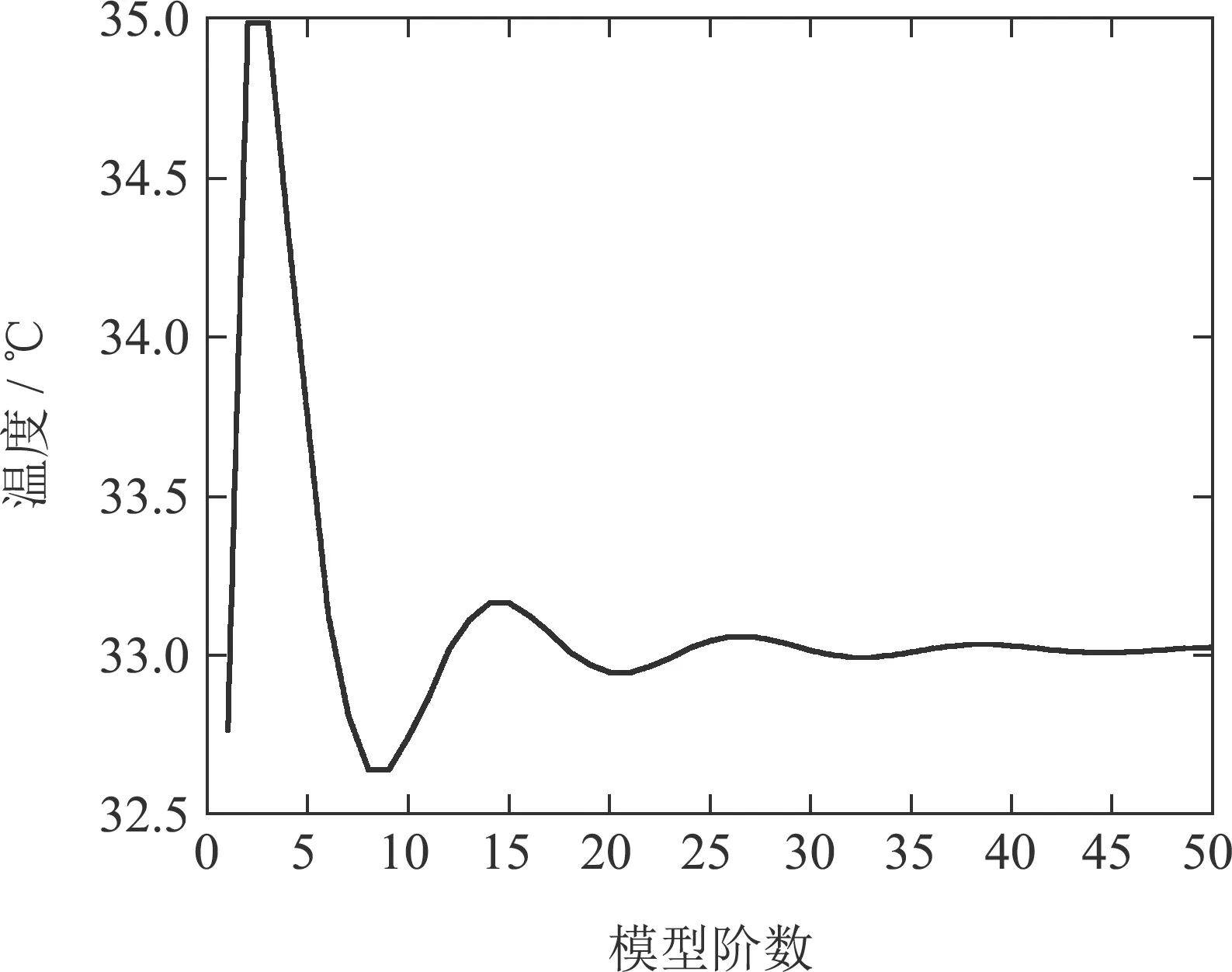
图3(b) 不同阶数下t=5 s,z=2 cm处温度趋势Fig.3(b) Temperature trend at t=5 s, z=2 cm under different orders

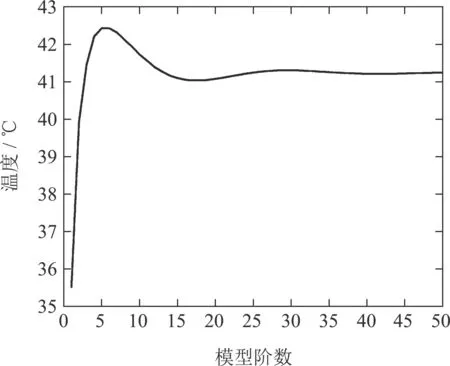
图3(c) 不同阶数下t=6 s,z=1 cm处温度趋势Fig.3(c) Temperature trend at t=6 s, z=1 cm under different orders

结合图2(a)-(c)可以看出当温度模型n=47时,温度逐渐趋于一致,只发生微小变化,其温度分布满足初始温度条件,因此将n=47时模型的温度分布作为近似标准温度分布并得到n=47时模型温度分布的计算时间为0.86 s.

在上述被加热媒质热力学参数、初始温度条件、非齐次边界条件、入射功率密度不变的情况下,分别求解n=3,n=8,n=13,n=18,n=23时有限维模型的温度分布和计算时间.在初始高维有限维ODE模型n=47的基础上通过空间基函数转换矩阵将有限维ODE温度模型进一步降维,并分别求解m=3,m=8,m=13,m=18,m=23时模型的温度分布与求解时间.m,n不同取值情况下模型温度分布与标准近似温度分布最大相对误差如图4(a)所示,m,n不同取值情况下模型计算时间如4(b)所示.

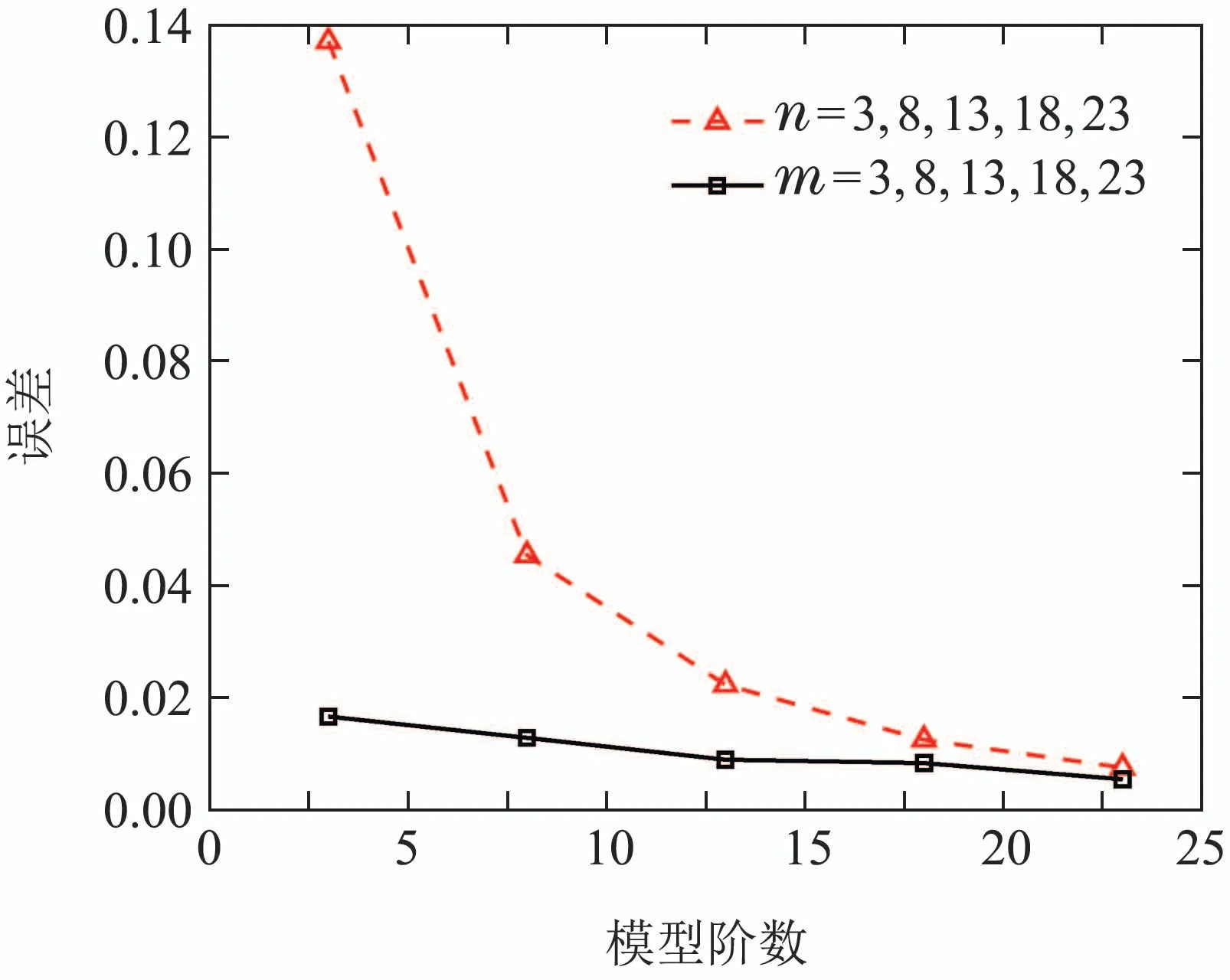
图4(a) m,n不同取值下与近似标准温度分布误差Fig.4(a) Error of approximate standard temperature distribution with different values of m and n

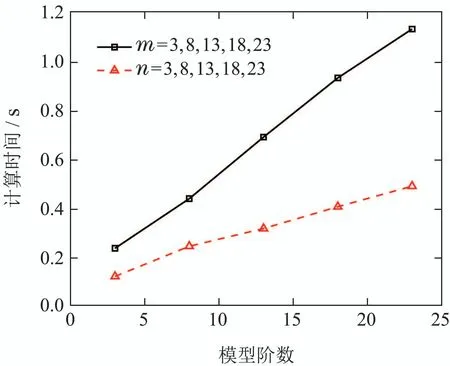
图4(b) m,n不同取值下的计算时间Fig.4(b) Calculation time under different values of m and n

m=3时模型的温度分布如图5(a)所示,并分别绘制n=3,m=3时模型的温度分布与近似标准温度分布的误差曲面图,如图5(b)-(c)所示.

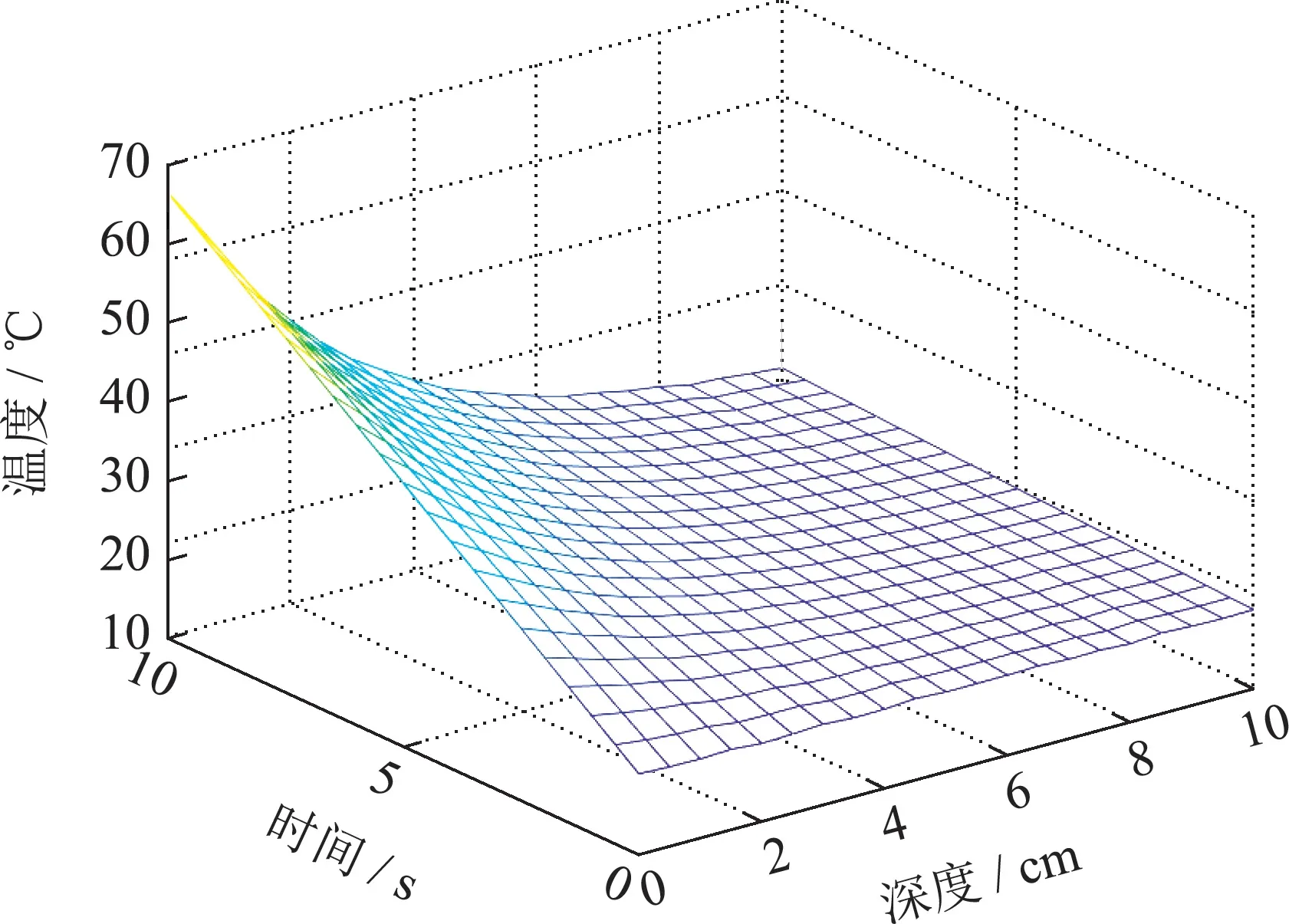
图5(a) m=3温度分布Fig.5(a) m=3 temperature distribution

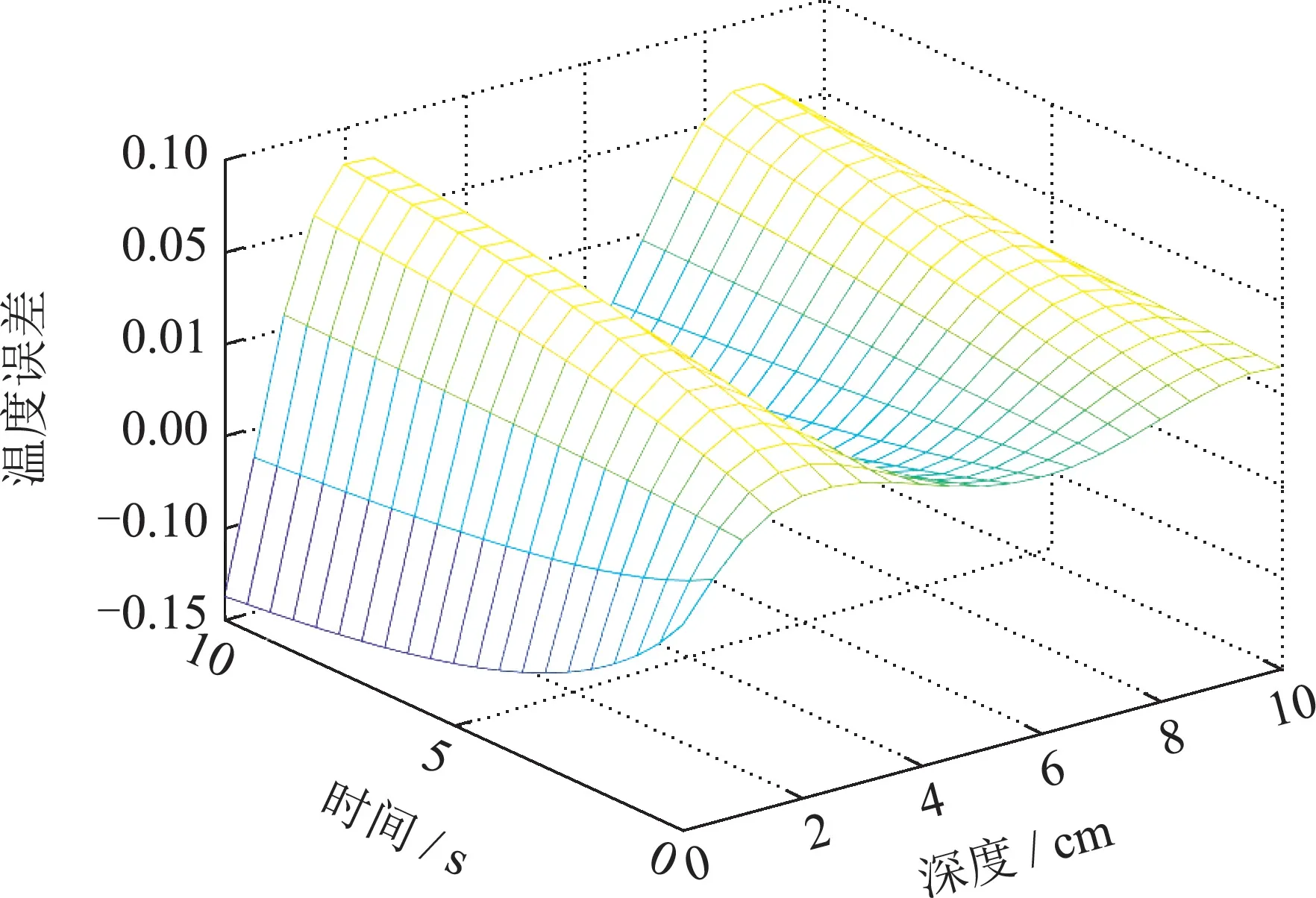
图5(b) n=3与近似标准温度分布误差Fig.5(b) Error of approximate standard temperature distribution with n=3

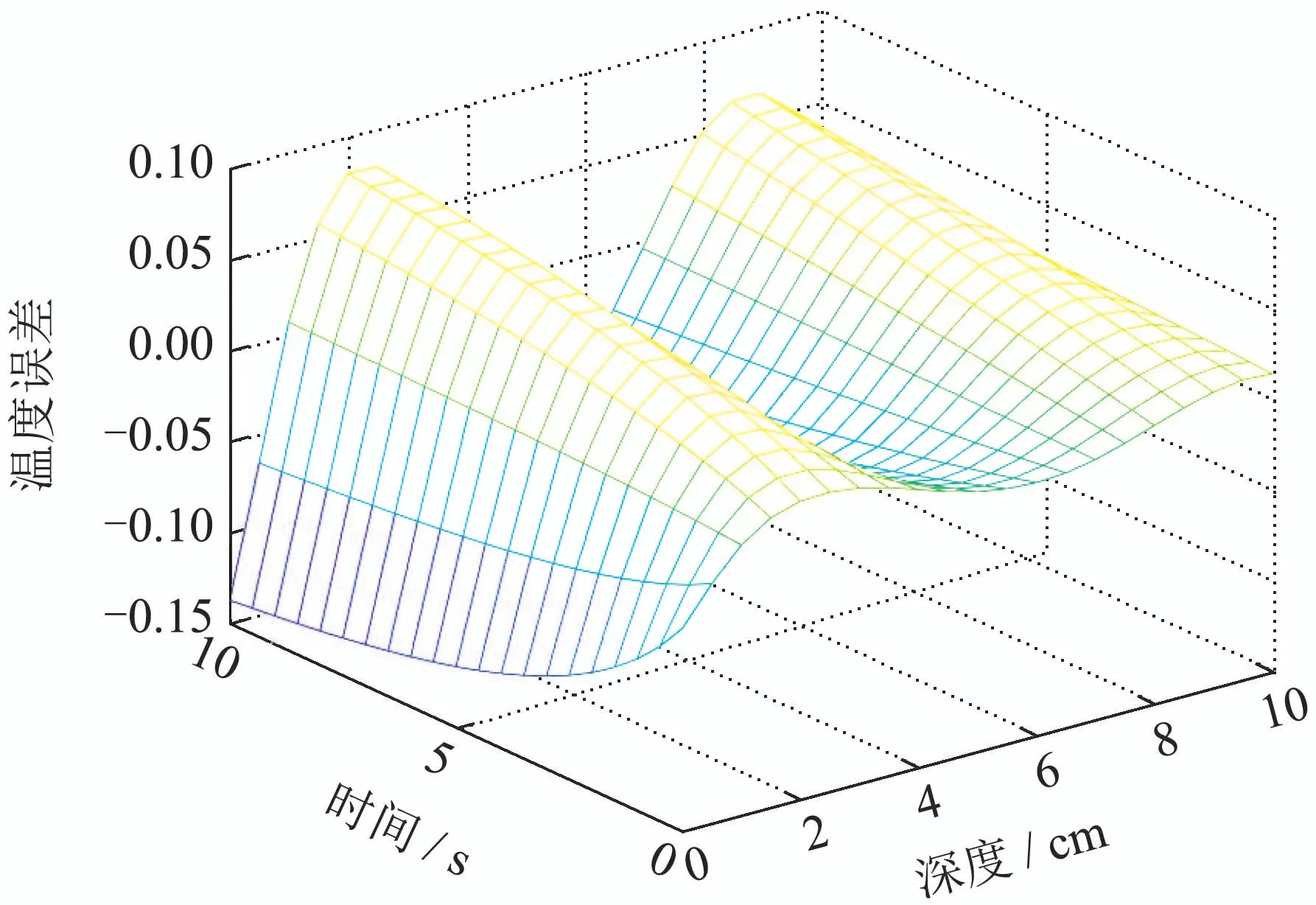
图5(c) m=3与近似标准温度分布误差Fig.5(c) Error of approximate standard temperature distribution with m=3

结合图4(a)-(b),5(b),5(c)可以看出m=3时最大误差为1.64%.而不经空间基函数优化组合直接取n=3时模型的温度分布与标准近似温度分布之间的误差较大,最大误差为−13.73%.并且m=3时模型计算时间和n=47时相比提升了72.2%.

4.2 模型验证

为了进一步验证所提出ODE温度模型(23)-(25)的准确性,在加热条件与有限维ODE温度模型完全相同的情况下,使用FEM对微波加热PDE温度模型(3)-(5)进行温度分布求解.

4.2.1 模型参数与边界条件

模型由微波反应腔体、去离子水及微波入射端三部分组成.反应腔体与微波入射端为长方体.为便于计算过程中的网格划分,去离子水并未充满整个反应腔体,与腔体壁之间留有极小的距离.去离子水与腔壁之间的介质为空气.包裹被加热去离子水的材料为聚四氟乙烯(PTFE),该材料介电损耗角很小,为透波材料,进行数值计算时可忽略其对微波加热过程的影响.腔体与WR340型标准波导使用铜材质,腔体规格为100 mm×86.4 mm×43.2 mm,馈送微波频率为2.45 GHz.系统从初始温度20°C开始加热,加热时间为10 s.铜与空气的热力学参数[22]为COMSOL内置参数,被加热去离子水热力学参数如上述表1所示,微波加热去离子水几何模型如图6(a)所示.

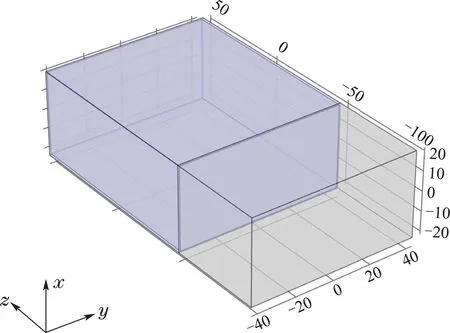
图6(a) 微波加热去离子水几何模型Fig.6(a) Geometric model of deionized water heated by microwave

边界条件分为电磁边界条件和热传导边界条件[22].针对电磁边界条件,反应腔壁和波导壁材质为铜,可视为完美导体,可由下列公式表达:

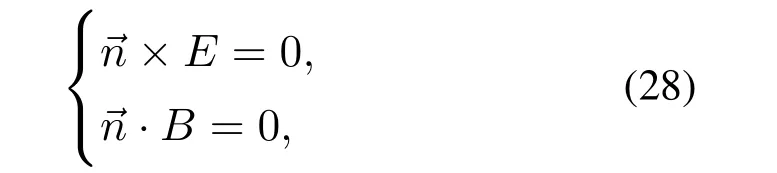
其中腔壁表面的单位法向量.

热传导边界条件可由下式表达:

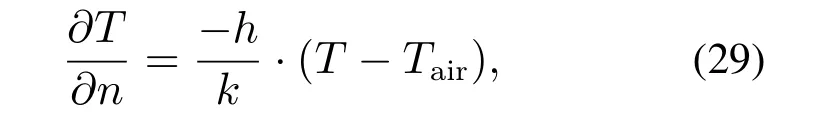
其中Tair表示反应腔体内空气介质的温度,h表示空气的热传系数(10 W/(m2·K)).同时,假设去离子水与腔体底部的接触边界热绝缘,即

4.2.2 数值计算结果与分析

利用第4.2.1小节中所提数值计算模型加热去离子水10 s,其整体表面温度分布与多水平切面温度分布如图6(b)所示.

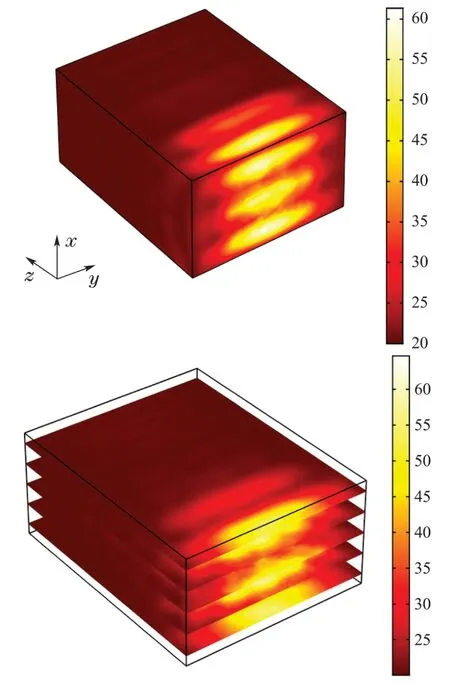
图6(b) 整体表面温度分布(上)与多水平切面温度分布(下)Fig.6(b) Overall surface temperature distribution(left)and multi-level section temperature distribution(right)

选取x=−15 mm时的水平切面,绘制z=0.5 cm,z=2 cm,z=4.5 cm,三点处10 s内的温升曲线并与m=3时ODE温度模型的温升曲线进行对比,如图7(a)-7(c)所示.

通过温升曲线对比图7(a)-7(c)可知,经空间基函数转换后的低维ODE温度模型与有限元模型相比也能精确的描述微波加热媒质的温升过程.因此,从数值分析的角度可验证本文所提出的微波加热ODE温度模型是正确且有效的.

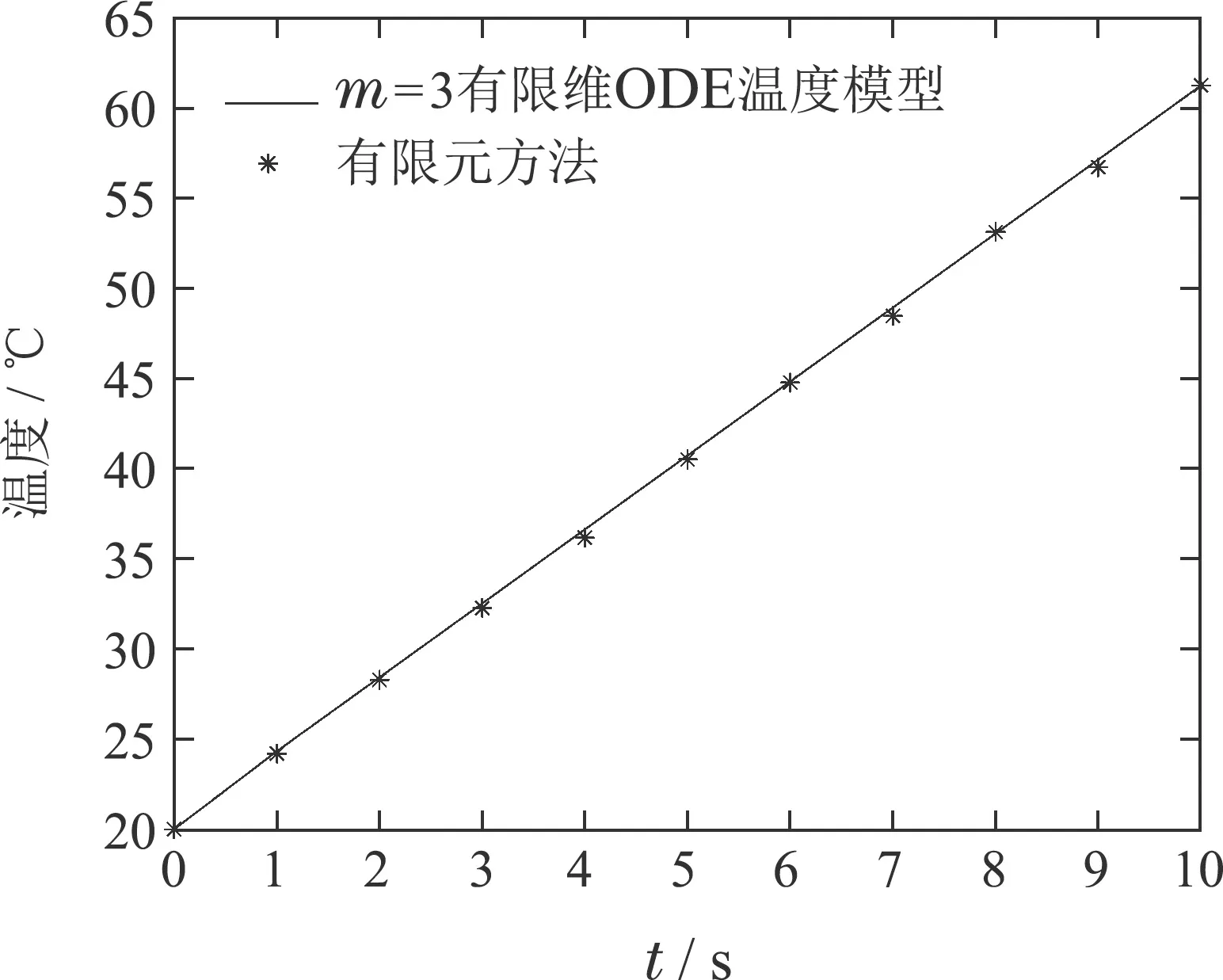
图7(a) z=0.5 cm时温升曲线对比Fig.7(a) Comparison of temperature rise curves at z=0.5 cm

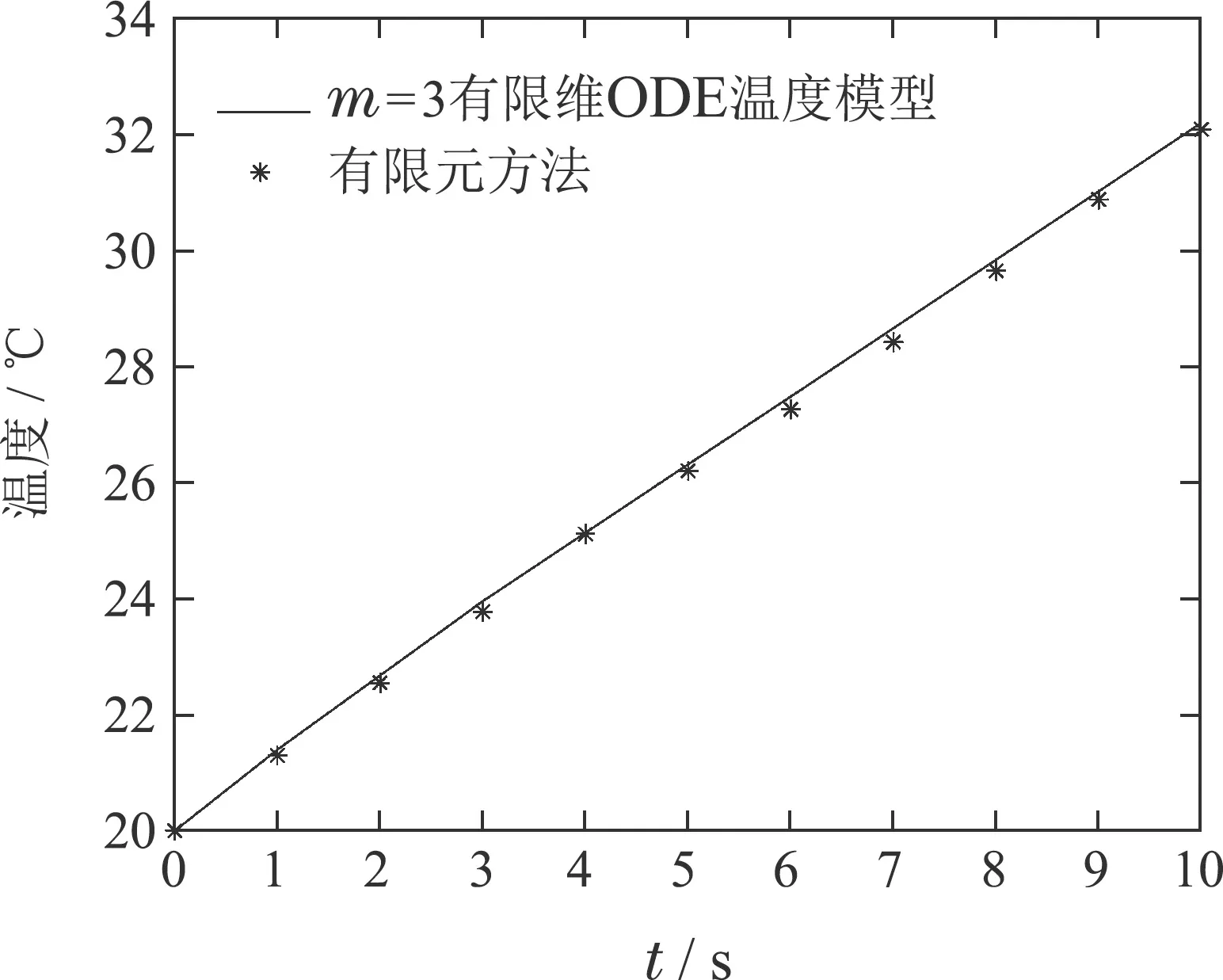
图7(c) z=4.5 cm时温升曲线对比Fig.7(c) Comparison of temperature rise curves at z=4.5 cm

5 结论

本文在有限维ODE模型的基础上,分析了有限维ODE温度模型阶数的选取对被加热媒质温度分布求解的影响,选取n=47时的模型的温度分布作为近似标准温度分布,并且利用空间基函数优化组合的方法对有限维ODE温度模型进一步降维,得到新的低维微波加热ODE温度模型.经仿真实验证明,优化组合后的m+1阶空间基函数对应的温度模型求解得到的温度分布与标准近似温度分布之间的误差维持在很小的范围内,m=3时最大误差为1.64%.而不经空间基函数优化组合直接取n=3时模型的温度分布与标准近似温度分布之间的误差较大,最大误差为−13.73%.并且m=3时模型计算时间和n=47时相比提升了72.2%.并且通过多物理场耦合FEM 求解微波加热PDE温度模型,进一步验证了优化后的低维ODE温度模型的准确性.本方法能在降低少许精度的情况下,大幅度提升温度分布求解速度,极大提高微波加热温度采集的实时性,具有较高的工业应用价值.