四轮驱动电动汽车稳定性预测控制器快速实现

许 芳 郭中一 于树友 陈 虹刘奇芳

(1.吉林大学汽车与仿真国家重点实验室,吉林长春 130025;2.吉林大学通信工程学院,吉林长春 130025;3.同济大学电子与信息工程学院,上海 200092)

1 引言

随着环境污染以及能源消耗问题的日益严峻,电动汽车越来越受到人们的关注[1].四轮驱动电动汽车的每一个轮子的驱动力矩都是可控的,可根据不同的环境对汽车每一个的轮胎驱动力进行控制,具有很强的灵活性[2].但是在汽车高速行驶的过程中,由于地面附着系数等不确定因素,汽车在冰雪路面或者湿滑路面进行急转弯操作中仍会出现车轮打滑导致车身侧翻现象,对车内乘客有极大的威胁甚至生命危险,因此,四轮驱动电动汽车行驶过程中的稳定性仍然是当前有待解决的问题.由于车辆横摆稳定控制是多输入多输出,而且还需要满足关键的安全约束及执行机构约束,而模型预测控制(model predictive control,MPC)具有前馈-反馈结构,能够处理多变量,显式考虑硬约束等特点,因此,基于模型预测控制的电动汽车横摆稳定控制成为研究热点.

由于模型预测控制需要在线求解优化问题,计算负担大,目前的研究主要集中于分层结构.分层结构的控制策略主要将上层横摆稳定控制与下层的驱动转矩优化分配分开处理,这种结构降低了控制器的阶次,减轻了系统的计算负担,易于实现.文献[3-5]采用分层控制结构,将上层横摆稳定控制器与下层转矩分配分开设计,最终通过汽车动力学仿真软件Carsim验证了控制器的有效性;文献[6]控制器上层采用极大值原理算法实现汽车横摆稳定控制,下层采用直接力矩分配方法,最后进行了实车实验.文献[7]上层采用模型预测控制器计算所需的纵向力和横摆力矩,下层根据上层控制器的输出优化调节每个车轮的扭矩,并进行了实车实验.文献[8]上层设计了基于模型预测控制的横摆力矩控制器,下层控制器通过最小化4个轮胎附着系数消耗率之和来分配车轮扭矩,最后完成了实车道路实验验证.分层控制器虽具有很好的快速性,但控制器的输出不能获得更好的平滑性,在一些极限工况下,由于整车和执行器间的动力学耦合特性,分层控制很难达到预期的控制效果.

统一结构控制策略将上层横摆稳定控制器设计与驱动力矩分配结合在一起,解决了整车和执行器间的动力学耦合,直接优化出系统的控制输入,相对于分层控制策略具有更好的平滑性.文献[9]提出了一种基于扩张状态观测器的线性预测控制器,对非线性系统模型进行线性化,降低了控制器计算负担.文献[10]设计了基于前轮主动转向和电机扭矩分配的整体控制结构的模型预测控制器,集成控制方案能够简化控制器的层次结构,具有更好的平滑性.文献[11]设计了基于MPC的转向控制器,采用集成的控制策略,旨在基于自适应车辆模型,通过主动转向和扭矩分配来保证横摆和纵向稳定性.集成的控制策略相对于分层结构具有更好的控制性能,但是车辆的集成控制是一个高度的非线性控制问题,然而,基于非线性预测控制器的车辆路径跟踪控制计算负担大,难以满足车辆快速动态系统的实时性要求,所以目前大多数研究都主要集中于仿真研究.因此,基于预测控制的电动汽车集成控制及其实时性问题亟需进一步研究.

针对以上问题,本文提出了基于快速预测控制的四轮驱动电动车横摆稳定控制器,实现了车辆横摆非线性预测控制器的实时计算,完成了硬件在环实验,具体工作包括:1)针对整车和执行器间的动力学耦合特性,以车辆状态跟踪和控制量约束惩罚为目标函数,设计了非线性预测模型控制器,实现了整车横摆稳定和电机转矩分配的一体化控制;2)将非线性规划问题转化为等式代数方程组求解,解耦预测空域间方程组的耦合关系,实现时域间优化问题的并行求解,通过现场可编程门阵列(field programmable gate array,FPGA)对算法进行硬件并行加速计算,实现了控制器的实时计算;3)搭建了硬件在环实验平台,实验验证了控制器的有效性,实现了车辆横摆稳定系统的实时控制,为实车试验奠定了基础.

本文的章节介绍如下:第2节主要介绍了系统总体控制策略以及车辆模型;第3节介绍了快速非线性模型预测控制器的设计过程;第4节对本文设计的控制器进行仿真验证;第5节通过硬件在环实验验证控制器的有效性及实时性;第6节对整篇论文进行总结.

2 集成控制策略

四轮驱动电动汽车控制的系统框图如图1所示.

图1 统一控制器系统框图Fig.1 Block diagram of the unified controller system

其中:δ为输入的方向盘转角,γ∗为期望的横摆角速度,β∗为期望的质心侧偏角,Tt为驾驶员输入的总力矩,Tfl,Tfr,Trr,Trl分别为4个轮胎的驱动力矩,δf为前轮转角,β和γ分别为汽车的质心侧偏角和横摆角速度,Vx为纵向速度,ax,ay分别为汽车的纵向加速度和横向加速度.

系统框图中驾驶员将方向盘转角和总驱动力矩输入到系统中,系统的参考模型将根据方向盘转角以及纵向速度计算出汽车保持安全行驶理想的质心侧偏角以及横摆角速度,快速非线性预测控制器由预测模型、目标函数、约束条件、并行牛顿法优化求解4部分组成.系统的预测模型和约束条件是构造目标函数的基础,系统的目标函数与约束条件共同组成了系统的优化问题,通过并行牛顿法对该优化问题求解,得出系统最优的前轮转角以及4个车轮的驱动力矩,最终将控制器输出的前轮转角以及4个轮胎的驱动力矩作用于车辆模型.

2.1 八自由度车辆模型

八自由度车辆模型[12-13]是为了验证控制器设计的有效性而使用的车辆模型,包括车体的横向、纵向、横摆、侧倾4个自由度以及4个车轮的旋转自由度,能够真实的还原实际的车辆模型,八自由度车辆模型示意图如图2所示.

图2 八自由度车辆模型Fig.2 Eight-degree-of-freedom vehicle model

2.2 二自由度车辆预测模型

系统的参考模型是为了根据方向盘转角以及纵向速度计算出汽车保持安全行驶理想的质心侧偏角以及横摆角速度.由于电动汽车的稳定性主要取决于汽车的质心侧偏角和横摆角速度,为了更方便的设计控制器,假设汽车两个转向轮转角相等,然后将前后轴左右轮简化为一个轮,因此得出了一个二自由度车辆模型,参考模型的计算公式以及二自由度模型参数可参考文献[9],二自由度车辆模型如图3所示.

图3 二自由度车辆模型Fig.3 Two-degree-of-freedom vehicle model

统一控制器选取β和γ作为系统的状态变量,在控制系统中,系统状态变量的平衡方程为

在控制器模型中侧向力的计算采用轮胎模型中的魔术公式,可以得出前后轮的侧向力为

Ka和Kb可以利用泰勒公式展开魔术公式获取.通过车辆的几何性质得出前轮和后轮的轮胎侧滑角为

4个轮子驱动力矩的总和应该等于驾驶员输入的力矩,设驾驶员输入的总力矩为Tt,因此车辆的驱动力矩可以表示为

因为本控制器采用统一的控制策略,并且横摆力矩可表示为

因此系统的控制模型可以表示为

3 快速预测模型控制器设计

本控制器采取统一结构的控制策略,取消了力矩分配这一环节,而是将4个轮胎的总力矩转化为每一个轮胎的驱动力矩,直接优化系统的控制输入,因此选取汽车的前轮转角和4个车轮的驱动力矩作为非线性模型预测控制器的控制变量,即u=[δfTxfrTxrrTxrlTxfl]T,同时系统的输出选择y=[β γ]T.因此非线性系统的控制器模型可表示为

函数f(x,u)如式(6)所示.

首先对车辆模型进行离散化,由于非线性模型预测控制器对系统的实时性要求较高,欧拉法离散化方法阶次较低,计算速度较快,因此本文采用向后欧拉离散化的方法,可得到系统离散化后的平衡方程为

式中的符号定义和参数值见表1所示.

表1 模型符号定义和参数表Table 1 Model symbol definition and parameters

由于目标函数直接决定了系统的性能,功耗等特性,因此目标函数的选择至关重要.在本系统中,定义p为系统的预测时域,则在k时刻的预测输出序列和参考输出序列可表示为

由于需要满足系统输出跟随参考输出的需求,使系统的输出尽可能的接近系统的参考输出来保证系统的稳定性.因此第1个目标函数可表示为

为了减小对执行机构的物理损坏,应该尽可能的在控制性能的基础上考虑被控输入的平滑性,减小系统被控输入的波动,设系统被控输入的变化量为

则被控输入在每个预测时域的变化量序列可表示为

系统输出的平滑性影响着车辆行驶的舒适性,目标函数需要考虑系统输出的平滑性,因此第2个目标函数可表示为

另外一个重要的因素是汽车的能源消耗,为了减小能源消耗以及减轻对环境的污染,应使系统输出的驱动力矩尽量小,因此第3个目标函数可表示为

其中垂向荷载Fzfl,Fzfr,Fzrl,Fzrr可由纵向加速度ax和横向加速度ay计算得到.

因此系统的总目标函数可表示为

在汽车的实际运行过程中,汽车的前轮转角以及驱动力矩受到物理条件的约束,由于执行器的饱和特性,前轮转角和驱动力矩都具有边界约束,不能越过执行器支撑的临界值.即

因此优化问题可描述为

其中i=1,2,···,p.由于预测模型控制的目标函数将每一个时域叠加在一起,计算负担十分巨大,计算时间长,不能满足大部分实时系统的要求,同时需要高性能的计算平台来对算法进行实施,因此对硬件的要求也十分苛刻.本文采用的并行牛顿法能够将预测模型控制的每一个时域展开进行并行计算,同时减小了算法的运算负担.可以大幅度减少模型预测控制的计算时间并且还拥有更好的控制性能.

并行牛顿法通过对系统的平衡方程和目标函数形式的转变以及每一个时域之间的耦合关系进行解耦,实现了该系统模型的并行计算[15].首先讨论该系统平衡方程和目标函数的变形,由于并行牛顿法不能处理不等式约束,在此采用内点惩罚函数的方法将系统边界约束转化为软约束,因此具有第4个目标函数,可表示为

因此该系统的总目标函数可表示为

Γu,ΓΔu,Γy,Γe分别为被控输入、被控输入变化量、系统输出以及系统软约束的权重系数序列.该目标函数不仅考虑到系统跟踪质心侧偏角、横摆角速度等保证车辆稳定性的关键因素,还考虑到系统的能源消耗,控制平滑性等因素,同时考虑被控输入的约束.

本文采用的并行牛顿法需要将每一个时域的目标函数分别求出最优的控制序列,需要把总目标函数拆分成单个时域的式子,在此表示为J′′,因此本系统的优化问题可由式(21)表示:

为了方便求解式(21),在此处引入拉格朗日乘子序列λi和µi(i ∈1,2···p)以及哈密顿函数

由KKT条件[14]将优化问题转化为代数方程求解

其中带脚标的H分别为对脚标变量的偏导数,由此可见该系统由一个求最优问题转化为一个方程组求解问题.由式(23)可以看出,相邻时域存在耦合关系,若要实现并行计算,需要对公式进行解耦处理,观察公式可得式中只有β∗(k −1),γ∗(k −1),(k+1),(k+1)与当前时域存在耦合关系,因此只需要将这4个变量在计算进行前预测出来,预测方法采用Gauss-Seidel 的思想,4个变量的预测值采用相邻时刻的值.求解后在对4个变量进行相应的补偿,即完成了公式中耦合关系的解耦,然后采用并行牛顿迭代法[15]进行方程组的求解.

代数方程并行求解算法步骤如下:

步骤1给定系统的初始状态vk0.

步骤2粗略迭代更新,通过预测出来的变量使用牛顿迭代法将每一个时域进行迭代求解.

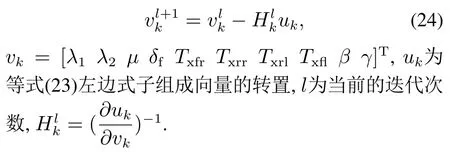
步骤3对λ和x进行补偿,根据连续两次迭代之间λ与x之间的差dλk与dxk进行补偿,减小由于λ和x的预测引起的误差对系统的影响.

步骤4判断误差是否满足迭代终止条件,若满足,则将迭代结果vk输出,否则,转步骤2.

在优化求解算法过程中,由于预测时域每一个时域之间彼此独立互不干扰,没有耦合关系,因此可以将N个时域展开进行并行计算,进而提高算法计算性能.

4 实验验证

为了验证本文设计的快速预测模型控制器的快速性,在MATLAB/Simulink平台中对该控制器进行仿真验证.本实验采用的车辆模型为八自由度车辆模型,其中包括车体的横向、纵向、横摆、侧倾4个自由度以及4个车轮的转动自由度,共八自由度.控制器预测模型采用二自由度车辆模型,控制器模型参数见表2.本次仿真实验将系统的参考方向盘转角和驾驶员输出的力矩直接输入给控制器,系统将根据参考的方向盘转角和输入的力矩输出最优的前轮转角以及4个车轮的驱动力矩,实现了整车横摆稳定和电机转矩分配的一体化控制,方向盘转角选择了最能反映车辆操作性侧翻的双移线工况和正弦工况.车辆行驶的速度65 km/h,设行驶路面平缓没有坡度,驾驶员输入参考力矩设置为340 Nm.

表2 控制器参数表Table 2 Controller parameters

4.1 干沥青路面方向盘双移线工况实验

干沥青路面的地面摩擦系数为0.8,方向盘转角采用的工况为双移线工况,具体的参考输入曲线如图4所示,双移线工况仿真结果如图5所示.

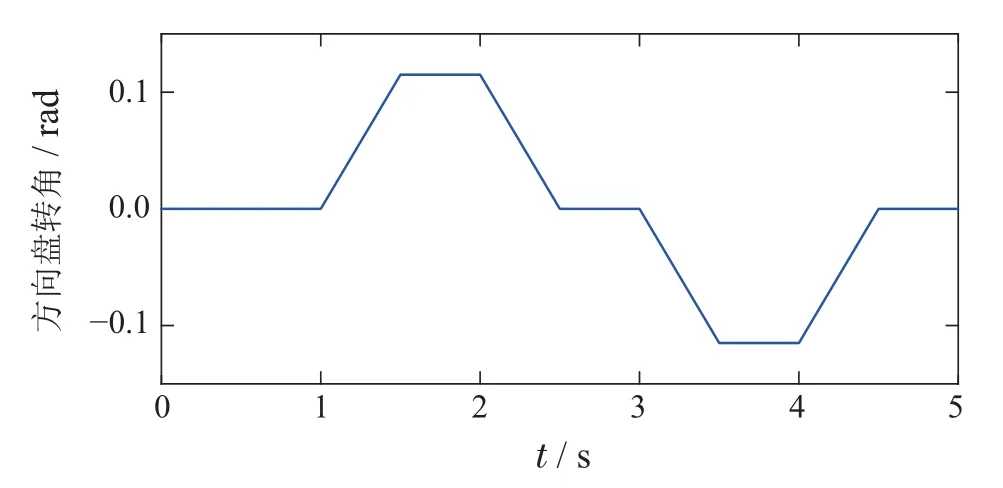
图4 方向盘转角输入曲线Fig.4 Steering wheel angle input curve

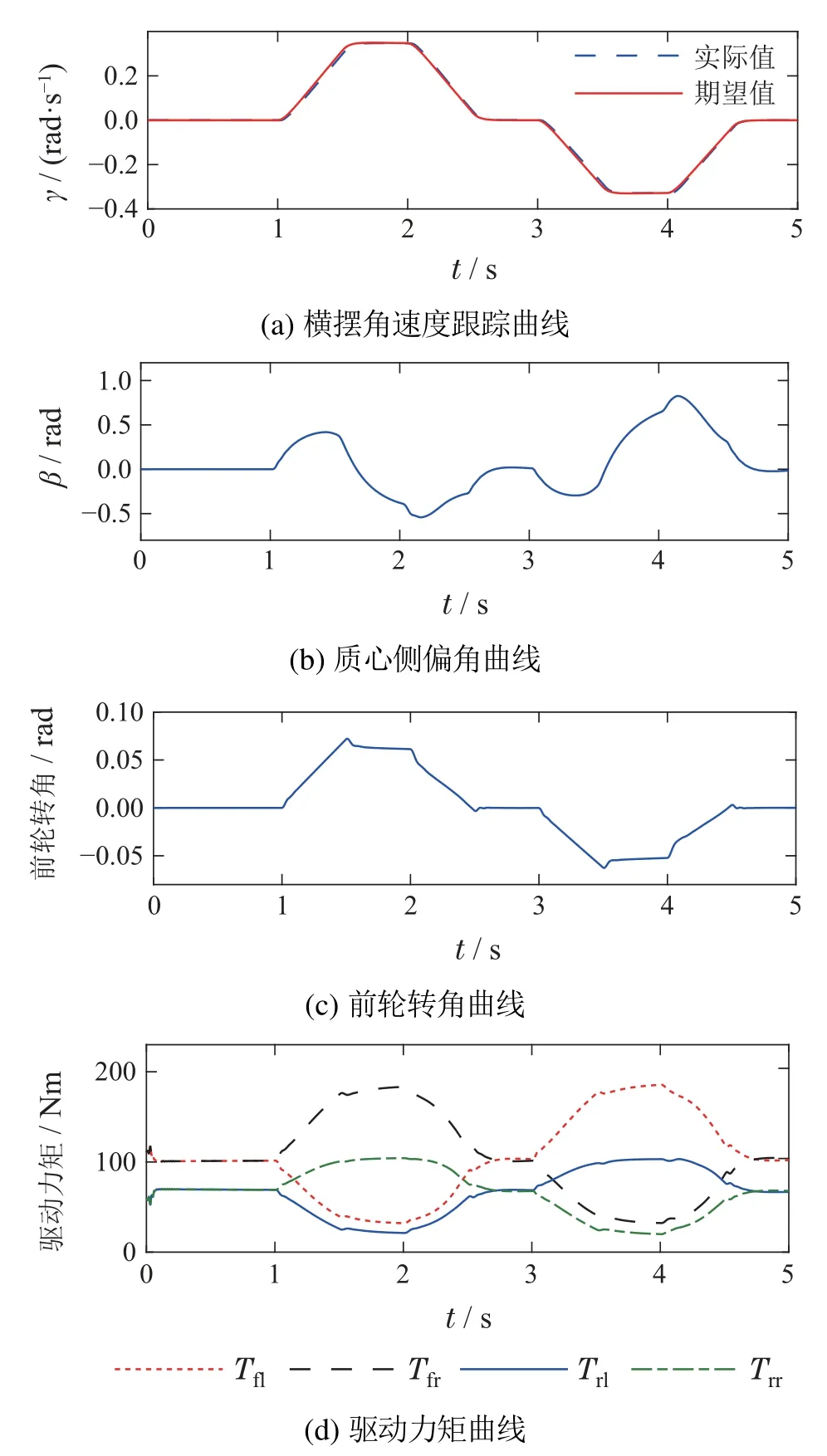
图5 干沥青路面双移线仿真结果Fig.5 Simulation results of double line shifting on dry asphalt pavement

影响汽车稳定性主要因素是车辆的质心侧偏角以及横摆角速度,为了保证汽车的稳定性,质心侧偏角的值应尽可能低,在汽车质心侧偏角被有效抑制的前提下,横摆角速度跟随期望横摆角速度的控制效果在稳定性控制中起着十分重要的作用.图5(a)为跟踪期望横摆角速度的仿真曲线图,可以看出该算法具有良好的跟随性能,图5(b)为质心侧偏角的仿真曲线,仿真图像验证了该算法可以很好的抑制质心侧偏角,将质心侧偏角保持在一个安全的范围内,可以保证电动汽车安全稳定的运行.图5(c)(d)分别为并行牛顿法算法系统输出的前轮转角以及4个轮子的驱动力矩仿真图,由图中可以看出系统输出的前轮转角峰值为0.07 rad,小于前轮转角约束0.1 rad,同时输出的驱动力矩峰值为190 Nm,小于系统输出的最大力矩200 Nm,在系统被控输入的约束范围之内,符合系统的要求.

为了证明并行牛顿法计算的快速性,本实验在MATLAB 平台将并行牛顿法,粒子群算法(particle swarm optimization,PSO)以及序列二次规划(sequential quadratic programming,SQP)的计算时间进行了对比,其中粒子群算法(PSO)参考文献[16],序列二次规划(SQP)参考文献[10],CPU主频为3.6 GHz.对比结果图如图6(a)所示.

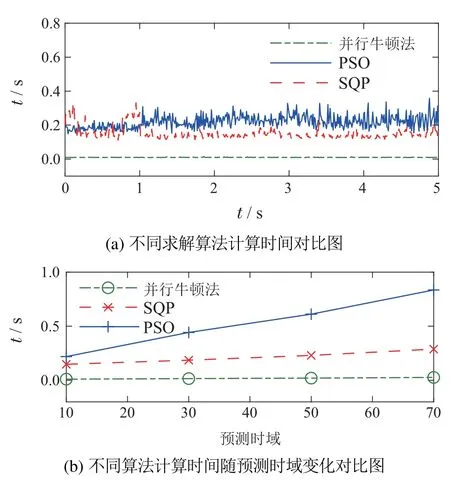
图6 计算时间对比结果Fig.6 Calculation time comparison result

由图中可以看出,并行牛顿法的计算时间远快于粒子群算法以及序列二次规划算法,通过计算得出并行牛顿法的平均计算时间为0.01 s,而SQP算法和粒子群算法的平均计算时间分别为0.1477 s和0.2189 s,计算时间大约提升了15倍.这证明了并行牛顿法可以明显减少系统的运行时间.可见该算法在拥有良好的控制性能之外,还能够大幅度提升系统的计算性能,缓解系统的时延问题.

图6(b)展示了3种算法的计算时间受预测时域的影响效果,在仿真实验中分别选用预测时域为10,30,50,70的节点.由图可以看出控制器的计算时间受系统预测时域的影响,且PSO算法的斜率最陡,而并行牛顿法最缓,因此可以得出并行牛顿法的计算时间相对于其他两种算法受预测时域的影响较小,更为稳定.

4.2 干沥青路面方向盘正弦曲线工况实验

干沥青路面的地面摩擦系数为0.8,选用正弦曲线作为方向盘的输入曲线,方向盘转角的幅值为0.1 rad,频率为2.61 Hz.图7为系统在方向盘正弦曲线工况下的实验结果,其中图7(a)为正弦方向盘输入下的横摆角速度跟踪曲线,图7(b)为实际的质心侧偏角曲线,图7(c)为系统输出的前轮转角曲线,图7(d)为系统4个轮胎的驱动力矩曲线.

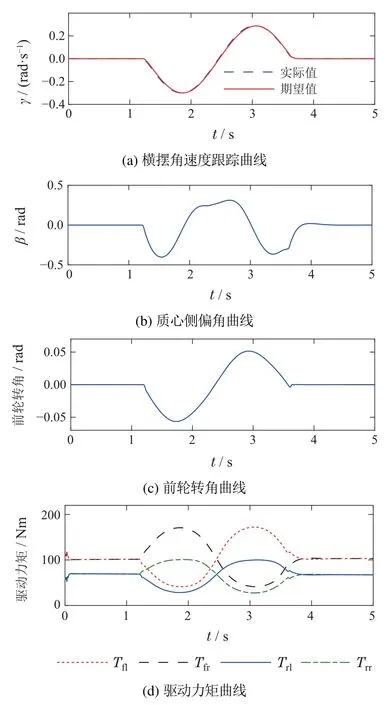
图7 干沥青路面正弦仿真结果Fig.7 Sinusoidal simulation results of dry asphalt pavement

仿真结果可以得出,在正弦方向盘转角输入的工况下,本文设计的控制器依旧可以很好的跟踪期望的横摆角速度,控制结果满足性能需求.在抑制质心侧偏角方面,控制器可以将质心侧偏角抑制在一个很小的范围,保证汽车的安全行驶.系统输出的前轮转角峰值在0.06 rad,不超过执行器约束0.1 rad,且系统单个轮胎的驱动力矩峰值为180 Nm,小于系统要求输出的最大转矩200 Nm,且4个轮胎的力矩之和为系统的输入力矩340 Nm,因此该控制器在常规工况下能够满足系统的要求.

4.3 湿滑路面方向盘双移线工况实验

为了验证该控制器在极限工况下的控制性能,选择在湿滑路面进行仿真验证,湿滑路面的地面摩擦系数为0.4,采用方向盘双移线工况,方向盘转角的幅值为0.1 rad,在方向盘转角基于参考值完成双移线工况的测试,系统的仿真结果如图8所示.

图8 湿滑路面下仿真结果曲线Fig.8 Simulation result curve under wet and slippery road

观察仿真结果可以得出,在湿滑路面的极限工况下,可以明显的观察到实际横摆角速度与期望值之间的误差,同时质心侧偏角的增加也较为明显,但针对于湿滑路面的极限工况而言,本文设计的控制器仍能够获得不错的跟踪效果.

为了验证本文设计的控制器与传统分层控制器的性能差别,本文对两种控制器的控制性能以及控制量输出进行了对比,图9为分层控制器在湿滑路面方向盘双移线工况下的仿真结果.

图9 分层结构湿滑路面下仿真结果曲线Fig.9 Simulation result curve under layered structure wet and slippery pavement

由实验结果可以看出,本文设计的控制器相对于传统分层结构的控制器而言,控制效果相差不大,但统一结构的控制器将所有被控输入都考虑在目标函数中,被控输入曲线相对于分层结构更加平缓,不仅减小了整车的能耗,而且提高了驾驶汽车时的舒适性.

5 硬件在环实验

5.1 实时实验结果

为了验证控制器的有效性和实时性,搭建了硬件在环实验平台,实验平台主要由ZYNQ开发板、Micro AutoBox和个人电脑3部分构成.其中ZYNQ由ARM和FPGA组成,运行本文设计的非线性模型预测控制器,MicroAutoBox运行八自由度车辆模型,个人电脑主要负责实验数据的监控.ZYNQ与MicroAutoBox之间通过CAN总线进行数据通信,硬件在环实验平台如图10所示.

图10 硬件在环实验平台Fig.10 Hardware-in-the-loop experiment platform

本实验中ZYNQ开发板采用的芯片型号为XCZU1 5EG,硬件在环实验的实验工况为干沥青路面方向盘双移线工况和正弦工况,实验结果如图11-12所示.

图11 双移线工况硬件在环实验结果Fig.11 Hardware-in-the-loop experiment results of double-shifting conditions

由双移线工况实验结果可以看出,由于数据传输时精度的降低,导致系统的质心侧偏角略微变大,同时输出的前轮转角不如仿真结果平滑,但横摆角速度跟踪效果较好,几乎无超调,总体控制效果与仿真结果相差不大,证明控制器设计满足系统实时性要求.在正弦工况下控制器仍能够取得优良的控制效果.正弦工况下硬件在环实验结果如图13所示.

图12 正弦工况硬件在环实验结果Fig.12 Results of hardware-in-the-loop experiments under sine conditions

5.2 计算性能分析

为了验证仿真环境与真实运行环境运算速度的区别,图13为Simulink的运算时间与C语言运算时间的对比结果.其中C语言运行在ARM CONTEX A53的CPU平台上,CPU主频为1.33 GHz.

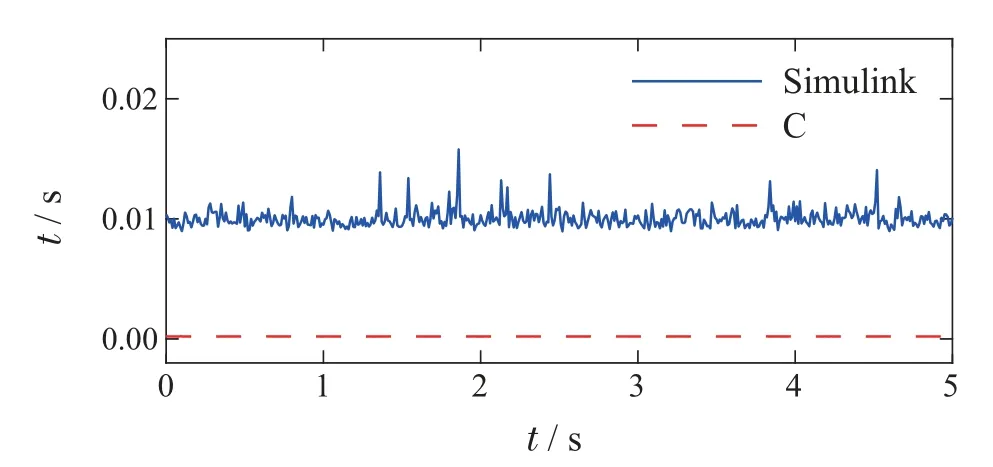
图13 Simulink仿真环境与C语言真实环境计算时间对比图Fig.13 Comparison of calculation time between Simulink simulation environment and C language real environment

由对比结果图可以看出,即便在主频更高的PC电脑上运行的MATLAB程序,依旧与C语言程序的运行效率有一定差距,原因主要是因为C语言本身是一种执行效率比较高的语言,相对于MATLAB程序运行速度更快,其次是Simulink仿真环境与真实的运行环境仍然有一定的差距,针对系统的实时性还是要按照实际运行环境来评估.

为了验证优化问题的并行求解性能,基于FPGA硬件并行计算平台,将并行求解算法中步骤2进行并行硬件加速实现.本次实验的预测时域为10,FPGA的时钟频率为100 MHz,由于需要综合考虑计算速度和硬件资源两个因素,将10个预测时域分为5块并行执行,并行计算前后的控制器单次求解时间以及资源消耗量结果见表3与表4.

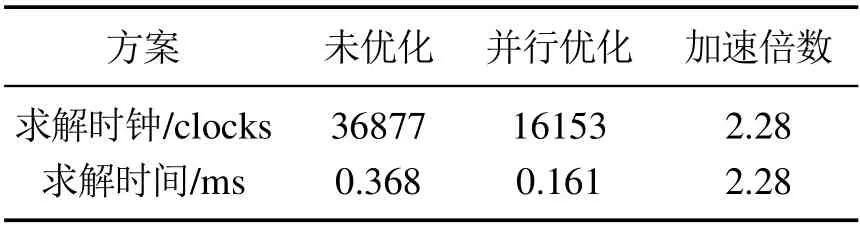
表3 控制器单次求解时间表Table 3 The single solution timetable of the controller

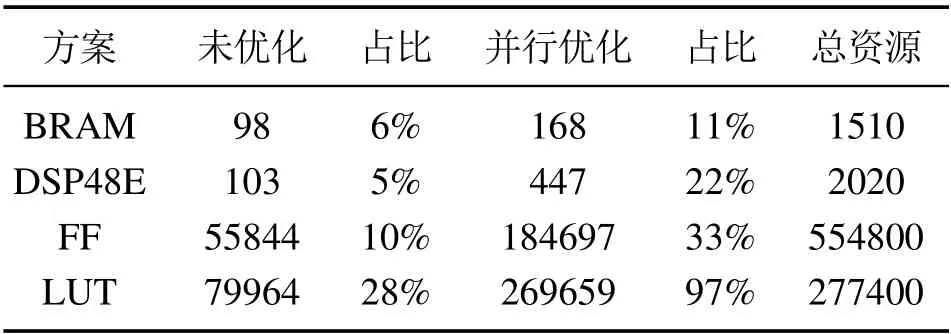
表4 控制器资源消耗对比表Table 4 Comparison table of controller resource consumption

并行过程是FPGA通过复制N块相同的电路实现的,因此由表中可以观察到,以并行度为5进行并行优化后,资源消耗率明显增多,其中LUT资源已经达到97%,而计算时间由原来的0.368 ms缩短为0.161 ms,计算性能提升了2.28倍,由于本文只对求解算法中迭代更新部分进行并行计算,可见FPGA是通过牺牲控制器硬件资源来换取控制器的计算时间.

6 总结

本文设计了一种基于快速预测控制的电动汽车横摆稳定控制器,采用统一结构的控制策略,将上层控制器与下层力矩分配结合在一起,提升了系统的控制性能;解耦预测时域内优化问题的耦合关系,通过时域间优化问题的并行求解,实现了控制器的毫秒级计算,提高了控制器的计算性能;基于ZYNQ搭建了硬件在环实验平台,利用FPGA的并行计算能力对算法进行硬件加速,给出了计算性能结果分析;最后完成了硬件在环实验,实现了车辆横摆稳定系统的实时控制,为实车实验奠定了基础.本文设计的快速非线性控制器相比于传统算法的控制器,系统的计算速度得到了大幅度提升,减小时延对系统的影响,使车辆行驶过程中能够更快的作出反应,提升汽车运行的安全性.下一步工作将采用精度更高的高阶控制器预测模型来进一步验证该控制器的有效性和实时性,同时将进行实车试验来验证控制器的可实施性.