一种带时间协同和角度约束的多导弹三维协同制导律
田 野,蔡远利,邓逸凡
(西安交通大学电信学部自动化科学与工程学院,陕西西安 710049)
1 引言
随着导弹技术不断发展,速度快、机动性强的目标给防御系统带来了极大挑战,传统的“一对一”作战方式逐渐难以完成高精度的拦截任务.针对未来战场上复杂多变的作战环境,不仅要求导弹能够对目标进行精确制导,还应与其他导弹协作完成多种作战任务.因此多弹协同拦截成为未来作战的一种有效策略[1-2],实现协同拦截的关键性技术之一是有效的协同制导律.对协同制导律的研究,目前主要包括基于拦截时间一致的协同制导[3],考虑攻击角约束和制导时间的协同制导等[4].
早期协同制导方法多采用预设每枚导弹拦截时间的思路,并依据所设时间为各弹分别设计制导律,制导过程中各弹间无相互通信,本质是转化为带时间约束的单枚导弹制导问题[5],在实际作战场景中受到了一定的限制.为实现真正意义的协同,结合比例导引律及其改进型、最优制导律[6]、滑模制导律[7]等理论的多种方法被逐步应用于时间和角度协同制导律中.文献[8]提出了一种由底层比例制导律和上层协调算法组成的协同制导方法,使用集中或分散式的协调策略实现上层协同控制,通过各弹的制导律实现底层制导.Zhang等[9]对有视场角约束的制导问题,结合期望命中时间与比例导引法PNG制导时间的误差项,提出了一种时间协同制导律.对制导与控制一体化的协同制导问题,Wang等[10]基于动态面理论设计了多导弹协同制导律.Guo等[11]应用超螺旋滑模面使各导弹与目标的相对距离趋近期望的弹目距离,构造了二维平面内的协同制导律,实现了对机动目标的拦截.在文献[12]中,基于弹目的相对运动设计了最优制导律来控制攻击角,并运用反馈线性化理论设计了状态反馈制导律来使各弹的拦截时间达到一致.
在制导时间协同方面,一种较有效的方法是建立弹间通信拓扑并基于多智能体一致性理论[13]使剩余飞行时间趋于一致,从而实现同时拦截目标的目的.文献[14]对有限时间一致性协议进行了研究并给出了一种基础形式,通过合理选取参数可使一致性协议具有连续的状态反馈形式.文献[15]将剩余飞行时间作为协调变量,应用一致性理论构造了多弹时间协同制导律,并基于经典线性滑模面设计了二维平面内的角度约束制导律,形成了内外双层的协同制导律结构,但该方法需要对各导弹的剩余飞行时间进行准确计算.文献[16-17]分别设计了同时约束攻击角度和制导时间二维协同制导律,包括第1层多智能体一致性协同算法和第2层的角度约束滑模制导律,但均未考虑拦截机动目标的情况.在上述二维协同制导律的基础上,国内外学者也开展了三维协同制导律的研究.Song等[18]使用超螺旋滑模设计了时间协同控制律,并构造了自适应滑模角度协同控制律,实现了三维空间内的多弹协同,但其滑模面形式较为复杂.文献[19]基于积分滑模设计了有向通信拓扑结构下的协同制导律,多枚导弹能够在同一时间击中目标并保证各弹的视线角满足期望值,不足之处是并未解决系统抖振现象.文献[20]中考虑了无向拓扑通信条件下的多导弹协同问题,基于非奇异终端滑模方法设计了视线纵向及法向的三维协同制导律,并引入了分段滑模趋近律,加快了滑模面收敛速度.
目前带角度约束的协同制导律研究多集中于有限时间收敛,然而也存在应用的局限性,其收敛时间上限依赖于系统初始条件.在某些制导初始条件不能精确获得的场景下,会影响对收敛时间的估计.由于固定时间稳定具有收敛时间上界不依赖初始条件的优点[21],因此将固定时间收敛理论应用于制导律设计逐渐受到了国内外学者的重视,所构造的固定时间收敛制导律具有较好的制导性能和广泛的适用范围[22-23].现有的协同算法中,在满足同时命中目标的基础上,大多数角度协同方法仅能保证各弹视线角分别在有限时间内收敛至期望值,而并未给出共同的协同时间上界[20],制导过程中各弹的角度收敛时间差别较大,对不同初始条件下的制导结果会有一定影响.同时,对单枚导弹拦截单一目标的固定时间制导问题研究并未进一步考虑多弹的时间协同一致[22].因此,在协同制导律中引入固定时间稳定的思想并设计相应的制导律具有理论和实际意义,也是本文研究内容之一.
综上所述,目前的研究仍存在不足:1)现有的协同制导律多基于二维平面内的运动模型,而实际拦截均发生在三维空间,因此需要深入研究三维运动模型下的协同制导律以满足实际工程需要;2)目前,针对拦截机动目标,并基于固定时间收敛思想设计的协同制导律的研究还十分有限;3)基于多智能体一致性理论所设计的时间一致协同制导律大多形式复杂,需要配置的参数较多,不便于实际应用.因此,本文针对以上3个主要问题展开研究.
针对多枚导弹拦截同一机动目标的制导问题,本文提出了一种带时间协同和视线角约束的协同制导律.采用双层方案,视线方向上基于一阶多智能体一致性理论设计时间协同制导律,保证各枚拦截弹同时击中目标;在视线法向方向,基于固定时间非奇异终端滑模设计了带末端视线角约束的法向制导律;通过构造收敛扩张状态观测器对目标机动进行估计.基于李亚普诺夫方法给出了稳定性证明.最后以三枚拦截弹拦截同一机动目标的场景进行了仿真,验证了提出方法的有效性.本文设计的协同制导律可应用于多弹协同拦截的工程实际中.
2 问题描述
2.1 协同拦截运动模型
针对三维空间的多弹协同制导问题,末制导阶段单枚导弹拦截机动目标的相对运动几何关系如图1所示.其中OXY Z为惯性参考坐标系,OXLYLZL为视线(line-of-sight,LOS)坐标系.M和T分别表示拦截弹和目标,R表示拦截弹和目标的相对距离,θL和φL为视线高低角和方位角.

图1 导弹和目标的拦截几何示意图Fig.1 Missile-target engagement geometry
由图1可得到单枚拦截弹拦截机动目标的三维相对运动学方程[18].

其中:aMr和u分别为视线方向和视线法向方向上的控制输入,aTr和D为视线方向和视线法向方向上与目标加速度有关的总干扰.
注1实际作战中,由于拦截弹和目标本身存在一定的几何外形,成功命中目标时弹目相对距离通常为R0,但存在制导精度可接受范围[Rmin,Rmax]=[0,0.1]m,在制导精度内表明成功拦截,即在整个末制导过程中均有R0.
拦截弹的剩余飞行时间可近似为

对式(6)求导,结合式(1)得到

命中时刻各弹视线角及角速率应满足

当n枚导弹拦截同一目标时,由式(4)和式(7)可得第i枚拦截弹与目标的相对运动学方程

综上分析,本文将分两部分进行设计:1)视线方向上的制导加速度指令aMri,使各枚拦截弹的剩余飞行时间达到一致;2)视线法向上的制导加速度指令ui,使各弹的视线角收敛至期望值,保证多弹以各自的期望视线角命中目标.
2.2 弹间通信描述及相关引理
多拦截弹协同制导中,各弹相互通信并交换状态信息,可看作一个多智能体的集合.对于如下包含n个智能体的一阶系统:

其中:xi为第i个智能体的状态量,ui为第i个智能体的一致性协议.
本文使用无向图G=(v,ζ,C)来描述弹间的通信拓扑关系.其中v={v1,v2,···,vn}是节点的集合,节点vi表示第i枚拦截弹;ζ表示节点间的连线,即弹间的通信关系;C=[cij]∈Rn×n表示权重系数矩阵,在无向图中,cij=cji >0表示拦截弹i和j之间能够进行信息通信,否则有cij=cji=0.若任意两弹之间存在至少一条通路,则该无向图是连通的.定义G对应的拉普拉斯矩阵L=[lij]∈Rn×n,其中矩阵元素

2) 如果图G是连通图,则λ(L)为L的第2个最小特征值且为正常数.
引理1[14]针对有n个成员的一阶多智能体系统(11),在其通信拓扑结构图G无向且连通时,设计如下控制输入:

引理3[18]假设系统存在连续正定函数V(t),且存在τ >0,0<η <1,使得(t)≤−τV η(t),则系统能够在有限时间tf内收敛至平衡点,收敛时间满足
引理4[22]考虑一类非线性系统

则系统(15)固定时间稳定且收敛时间T有界,满足

3 三维协同制导律设计
3.1 视线方向有限时间协同制导律
针对制导子系统(9),本节设计视线方向上的时间协同制导律使各拦截弹剩余飞行时间在有限时间内达到一致,并构造一种扩展状态观测器对包含目标加速度的外部干扰进行估计.
用tfi表示第i枚拦截弹命中目标的时刻,t表示当前时刻,tgoi表示其剩余飞行时间,则有

基于引理1构造考虑目标扰动的多智能体有限时间收敛一致性协议

定理1针对视线方向上的子系统(9),在其通信拓扑结构图G无向且连通时,选择式(19)为制导律,则各枚拦截弹的制导剩余飞行时间能够在有限时间内达到一致.
证令xi=tfi,由式(17)和式(19)可得


为了消除目标机动对系统产生的影响,通过构造一种扩张状态观测器对目标视线方向总干扰dri进行估计,将得到的估计值加入制导律中对dri进行补偿,以得到理想的制导效果.
考虑如下一阶非线性动态系统:

式中:x为状态量,f(x)为已知函数,w为未知总体不确定性,u为控制输入.
式(30)可以扩张为一个二阶动态系统[25]

式中:x1=x,x2=w,τ=.
针对制导子系统(9),构造扩张状态观测器

注2视线方向干扰估计值能够在有限时间内收敛到实际值dri.由文献[26]定理4.1可知,若扩张状态观测器(32)的估计误差满足有限时间收敛,则观测器可与控制器分开设计,满足分离原理.同时,扩张状态观测器可在线估计并补偿外界不确定性.
3.2 视线法向方向有限时间协同制导律
本小节针对制导子系统(10),对各弹设计固定时间视线角约束制导律,使得每枚拦截弹的视线角均能在固定时间内收敛至期望角度,从而实现了空间上的协同.相对于有限时间的角度约束制导律,固定时间制导律的收敛时间上界独立于制导初始条件,可通过合理设计参数预先设定.在同时命中目标的基础上,多导弹固定时间内实现特定角度的协同拦截,具有更广泛的场景适应性,从而最大化多弹拦截能力.
设第i枚导弹的期望视线角为[θLfi φLfi]T,视线角误差可表示为

选择如下固定时间终端滑模面[22]:


为了消除制导子系统(10)中因目标机动引起的总干扰Di,设计扩张状态观测器分别对目标俯仰和偏航方向的外界干扰进行估计.

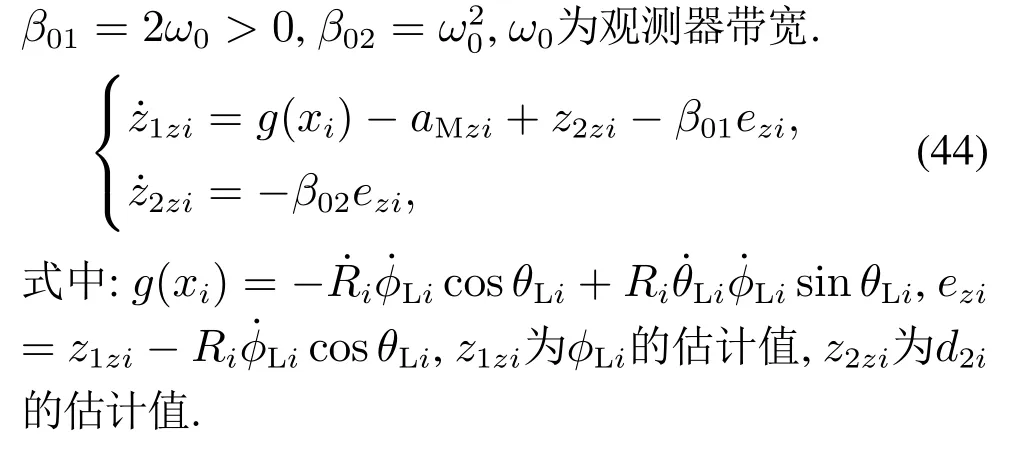
定理2针对视线法向方向上的子系统(10),选择式(33)作为滑模面,(42)为制导律并利用扩张状态观测器(43)-(44)对制导子系统中的外界干扰进行估计,可使各弹的视线角θLi和φLi在固定时间内收敛至期望终端视线角,视线角速率固定时间内收敛到零,各弹以期望的视线角协同命中目标.
证Lyapunov函数选取如下:

结合引理4和文献[27]定理1可得,系统状态在固定时间内到达滑模面.

考虑如下Lyapunov函数:

由引理4可知制导系统状态量x1i和x2i将在固定时间内收敛,在滑模面运动的收敛时间上界为
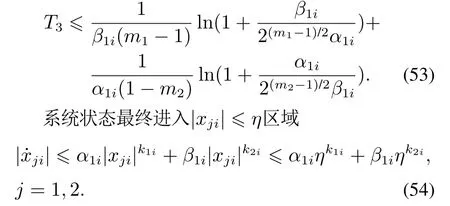
综合可得制导系统的整体收敛时间上界为

类似的,制导系统的状态量x1i和x2i将在固定时间内收敛,制导系统的整体收敛时间上界为Ts.综上所述,x1i和x2i能够在固定时间Ts内收敛至系统平衡点.即视线角θLi,φLi在固定时间内收敛到期望的终端视线角,视线角变化率θLfi,φLfi趋于零. 证毕.
注3制导律(43)的固定收敛时间上界Ts决定于设计参数α1i,β1i,m1,m2和α2i,β2i,n1,n2的选择,与初始制导条件无关.对的设计需要结合作战实际环境进行综合考虑,在某些特殊情况如初始视线角跟踪误差较大时,受限于导弹的实际机动能力,制导指令可能会出现持续饱和现象;若Ts设置过短,则导弹可能在很短的末制导时间内无法以期望的角度命中目标.因此,需要通过对收敛速度和控制品质的权衡来合理选择参数.同时,预先设定了角度约束的时间上限,可与视线方向的时间协同制导律综合考虑,使制导系统的整体剩余飞行时间和角度收敛时间处于一个合理的范围内.
4 仿真分析
本节针对三枚导弹拦截同一个机动目标的情形进行数学仿真.导弹间的通信网络拓扑结构如图2所示,该网络是无向且联通的,对应的权系数矩阵可描述为式(58),仿真初始条件见表1.


图2 导弹间通信拓扑结构Fig.2 Communication topologies for three missiles

表1 仿真条件Table 1 Initial parameters of the missiles
沿视线及法向方向的目标加速度大小为

制导律参数选取为m1=n1=9/7,m2=n2=7/9,η=0.1,α1i=β1i=14,α2i=β2i=0.35,扩张观测器带宽,导弹制导加速度上限为25g,g=10 m/s2.由给定参数得到的视线角收敛时间上界Ts=16.26 s.
使用本文构造的协同制导律,三枚拦截弹在末制导初始位置不同的情况下,能够以期望的视线角同时击中目标.仿真结果如图3(a)-(i)所示.
图3(a)为三枚拦截弹的剩余飞行时间,从图中可以看出,各弹的剩余飞行时间在进入末制导后约3 s时达到一致.从图3(b)可以看出各弹的弹目相对距离随着飞行时间的增大逐渐减小,并在15.3 s左右同时击中目标,实现了时间协同.图3(c)-(e)给出了各拦截弹在视线方向和视线法向方向的加速度曲线.由于存在目标机动,且要满足固定时间内的角度快速收敛,在制导开始的一段时间内需要较大的加速度,法向过载出现了短暂饱和现象,但饱和数值在合理区域内.在协同制导律作用下三枚导弹的剩余飞行时间快速趋于一致,并在短时间内通过观测器实现了对目标机动的估计后,各加速度指令便收敛至较小范围内.在制导律作用下加速度曲线并未出现连续大幅度抖振现象,个别拦截弹初始偏差较大,为了使各拦截弹的角度在固定时间上界内收敛,在制导中段出现了短暂的加速度指令突变.图3(f)-(g)为视线俯仰角和视线方位角曲线图,从图中可以看到3枚拦截弹的视线角均在固定时间上限内收敛至期望值,满足了视线角约束的要求.图3(h)-(i)给出了视线角速率随时间变化的曲线,可以看出各弹的视线角速率均在固定时间上限内趋于零,对视线角及视线角速度的控制是有效的.



图3 本文设计协同制导律仿真曲线Fig.3 Simulation results under the proposed cooperative guidance law
协同制导仿真结果见表2,可以看出各拦截弹的制导时间相同,拦截时刻的脱靶量和视线角误差均在合理范围内,具有较高的制导精度.验证了在所设置的仿真条件下,各弹可以从期望的方向同时击中机动目标.
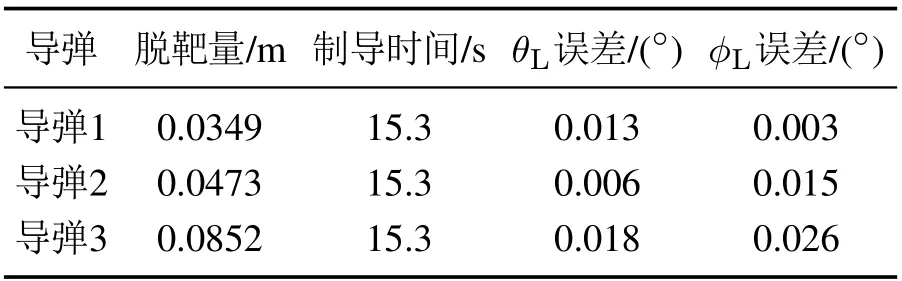
表2 脱靶量、制导时间和角度误差Table 2 Miss distance,interception times and LOS angle errors
文献[18]中,Song等为了实现攻击时间和角度约束协同,在视线方向和视线法向方向分别基于积分滑模和终端滑模设计了有限时间协同制导律.本小节使用文献[18]提出的方法,基于同样仿真初始条件和期望终端数值进行了拦截仿真,仿真结果如图4(a)-(i)所示.
通过与本文提出方法的仿真结果对比,可以看出两种方法拦截时间和剩余飞行时间达到一致的速率基本相同,但本文在视线方向上的时间协同制导律形式更为简单,便于实际参数配置应用.对比视线法向方向加速度变化曲线图4(c)-(d)可知,本文方法中的加速度曲线饱和持续时间更短,从图4(e)-(i)可以看出,本文制导律下的视线角速率与视线角收敛速度更快,且具有收敛时间上界可设定的优点.因此相对于已有的典型协同制导方法,具有一定的优越性.
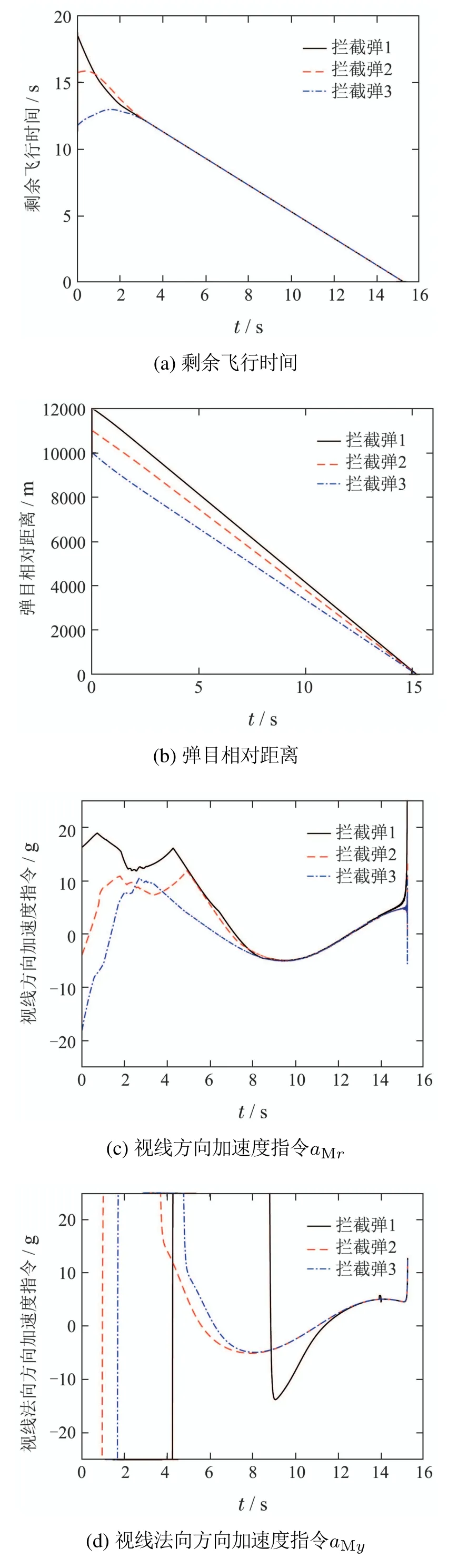


图4 Song方法协同制导律仿真曲线Fig.4 Simulation results under Song’s guidance law
5 结论
本文针对具有弹间通信的多弹协同拦截同一机动目标问题进行了研究.在视线方向,基于多智能体一致性理论设计了有限时间协同制导律,各导弹剩余飞行时间能够在有限时间内达到一致,从而实现同时打击;在视线法向方向,基于固定时间非奇异快速终端滑模设计了带角度约束的制导律,可使各弹的视线角在固定时间内收敛至期望值;同时,构造了扩张状态观测器实现了对目标机动的估计.最后对三枚拦截弹协同拦截同一机动目标的情况进行仿真并与典型方法进行对比,验证了所设计带角度约束和时间协同制导律的有效性和优越性.后续将对满足视线方向固定时间协同的制导律展开进一步研究.

