基于改进动态运动基元的6D轨迹规划

王健发,王耀南,陈文锐,刁 强

(湖南大学电气与信息工程学院,机器人视觉感知与控制技术国家工程实验室,湖南长沙 410082)

1 引言

随着机械臂技术的飞速发展,机械臂的应用在各个行业得到了广泛的推广.相应地,机械臂作业任务的复杂性不断增大,这都对其规划和控制提出了更高的要求.而示教学习方法通过建模学习人类的操作技能,可以高效地应用于不同的机械臂本体[1],有效减少机械臂轨迹规划的难度,近年来逐渐发展为机器人学中的重要研究内容之一[2-4].

目前典型的机械臂轨迹示教学习方法主要包括基于样条[5-6]、基于统计模型[7-10]、基于仿射变换[11-12]和基于动态运动基元[13-14]的轨迹学习方法4类.其中基于样条的轨迹学习方法是通过样条函数拟合采集到的人体运动数据实现的,规划生成的轨迹平滑性好,但泛化能力不足.基于统计模型的轨迹学习方法主要是利用高斯混合模型或隐马尔可夫模型拟合运动的各个特征进行学习的轨迹规划方法,计算效率相对较低,且生成的轨迹不连续.基于仿射变换的轨迹学习方法是依据人体运动的仿射不变性开发的轨迹规划方法,其不依赖于具体模型,可以直接变换关节角时间序列.但是由于人体与机械臂在结构和运动能力上的差异性,该方法无法快速的将人体运动映射成机械臂运动.

与上述方法相比,Ijspeert等[13]于2002年首次提出的(dynamic movement primitives,DMPs)是一种以非线性微分方程形式的动态系统来编码运动的策略,其计算效率高、生成的轨迹连续、泛化简单[14],被广泛用于机械臂的移动与操作上.Ude等[15]在DMPs中引入了查询子的概念来同时考虑任务参数和模型参数,并依据任务变化进行参数调整,该方法在扔球实验上得到了验证.Gaspar等[16]将运动中的空间信息和时间信息分开表示,提出了弧长参数化的DMPs模型,解决了示教中运动速度差异大的问题,该方案在类人机器人CB-i 上臂的移动与动作识别上得到了验证.Kober等[17]在DMPs系统中耦合了感知单元,提高了系统的抗干扰能力.此外,他们还依据强化学习方法对权重进行了探索,优化了系统的控制策略,该方案在模拟的SARCOS机器人手臂学习Ball-in-a-Cup游戏上性能良好.Li等[18]利用DMPs学习关节轨迹、PI2算法学习带有操作不确定性轨迹的策略,实现了机械臂与机械手关节空间轨迹的同步优化,该方案在移动机器人的抓取操作上得到了验证.Zeng等[19]在DMPs的基础上,引入了柔顺适应模块,使得机械臂可以在与物理环境接触时学习复杂的操作技能,在Baxter机器人倒水、锯木头等实验上得到了验证.

尽管DMPs算法已经得到了广泛的应用,但其仍然存在一些问题.在动力学模型中,没有明确区分位置与姿态轨迹方案,无法做到姿态的无奇异表示.对于跨零点问题欠缺考虑,即目标与初始状态差值项近似为0时,目标状态小的波动容易产生加速度抖动.差值项等于0时,加速度恒等于0.差值项变号时,轨迹会发生翻转.此外,机械臂避障行为过早发生,会造成过多的消耗.目前,针对上述问题的研究相对较少,主要包括以下几种方法.Hoffmann等[20]改进了现有位置DMPs中的转换系统,解决了位置上的跨零点问题,但对姿态轨迹则欠缺考虑.此外,在动力学模型中耦合了偏角避障因子,实现了避障控制,但由于忽视了机械臂与障碍间距离因素,避障行为过早出现.Ude等[21-22]提出了四元数DMPs模型,无奇异地编码了姿态轨迹,然而忽略了跨零点问题.

针对上述问题,本文提出了基于改进DMPs的6D轨迹规划方法.在动力学模型中以四元数的方式明确区分了位置与姿态轨迹,实现了6D轨迹的无奇异表示.此外,改进了转换系统,克服了跨零点引起的抖动、轨迹翻转等问题.最后,依据机械臂和障碍物间的距离与偏角建立虚拟阻抗关系,实现了机械臂的避障控制,消除了过早的避障行为.

2 笛卡尔空间动态运动基元建模

2.1 一维动态运动基元

依据Hoffmann等[20]对标准DMPs的改进,一维运动的DMP可以表示为

其中:α ＞0是预定义的常数,g是目标位置,y0是初始位置,x是相变量,z是缩放后的速度,τ=tT是表征运动持续时间的缩放因子,可以用于轨迹加速度、速度和时间的缩放而不改变其形状.kv是弹性常数,dv是阻尼常数.当系数4kv=,就可以得到临界阻尼系统.其中,f(x)是由n个力场线性组合得到的力场综合中心点与相变量的乘积,与标准DMP中强迫函数不同的是其不再直接关联差值项(g −y0),

其中:wi是力场中心点,ψi(x)是钟型脉冲函数.函数f(x)并不直接取决于时间变量,而是相变量x,积分正则系统τ=−αx得

注意:为了与标准DMP统一称呼,在下文中,f(x)也称为强迫函数,wi也称为权值系数,ψi(x)也称为径向基函数.

2.2 6D轨迹动态运动基元

机械臂的轨迹规划不仅需要考虑其3D位置变化,也需要考虑其运动过程中的3D姿态变化.

在位置轨迹上,常用的DMPs规划方案是将多维的运动解耦成多个独立的一维运动,然后分别在每个维度上进行学习,计算各自的转换系统,最后计算各个维度上的运动轨迹.为保证各独立的一维运动间的同步,整个过程由同一个正则系统驱动,相应的多维位置DMPs可以定义为

式中相关参数与式(1)-(3)中类似,gp,p,p0分别表示多维的目标位置、当前位置和初始位置矢量.v是速度矢量.K和D分别表示弹性系数矩阵和阻尼系数矩阵.相应的强迫函数fp(x)定义如下:

其中R3是位置权值系数矢量.

与多维位置DMPs不同,由于姿态集SO(3)是一个三维流形,具有特殊的流形结构,无法用3个参数无奇异表示[21],因此上述解耦方案就不适用了.本文选择单位四元数q=u+v ∈S3(u ∈R3,v ∈R)对姿态进行描述,并在更高维的空间对q的计算添加额外的约束,以确保其没有偏离SO(3)结构.与Ude等[21]的姿态DMPs不同的是,本文算法中强迫函数不再关联姿态间距,避免了跨零点问题.

式中:go,q和q0分别表示目标姿态、当前姿态和初始姿态矢量;K和D分别对应弹性系数矩阵和阻尼系数矩阵.强迫函数fo(x)定义如下:

则姿态q2到q1的距离度量对应的旋转矢量可以表示为

则dt时间对应的平均角速度可以表示为

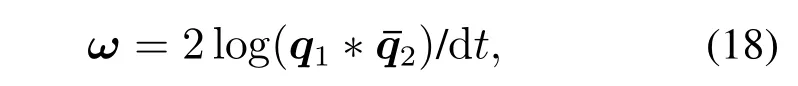
由式(16)可知,当限制其定义域为S3/([0 0 0]T−1)时,四元数对数映射是一对一且连续可微的.因此,相应的逆映射,即,指数映射exp:R3→S3可以定义为

这里限制‖r‖≤π.依据式(19),从角速度到四元数的映射χ可以表示为

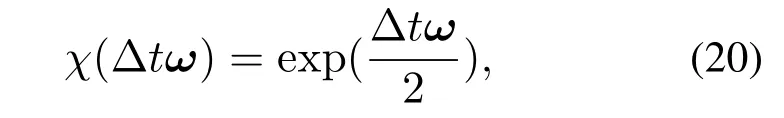
式中Δtω表示以角速度ω旋转时间间隔Δt对应的旋转矢量.

2.3 空间避障

在机械臂运动的在某个时刻,障碍物位置o与机械臂末端位置e之间的矢量(o −e)和机械臂末端速度矢量v的偏角为φ,如图1所示.依据虚拟阻抗思想,虚拟接触力f(t)定义为机械臂末端与障碍物间距离的函数,虚拟阻抗定义为接触力-偏角与偏转加速度之间的动态关系.由此,在原有位置DMPs的基础上,引入一个偏转加速度,使得机械臂末端的运行轨迹发生偏转,避开障碍物.相应的虚拟接触力大小‖f(t)‖定义为

其中:常数a和b是辅助参数,d(t)是障碍物与机器人之间的距离,且满足‖f(t)‖=a −bdmax=0.机械臂运动方向与障碍物之间的偏角φ定义如下:

在避障控制算法中,当虚拟接触力‖f(t)‖大于0且偏角φ小于π/2时,可以将虚拟接触力分解为速度方向的力fv以及垂直运动方向的力fr,如图1所示,偏转加速度p(e,v)定义为

图1 机械臂与障碍物之间位置和虚拟力的关系Fig.1 The relationship of the position and virtual force between the manipulator and the obstacle

式中:k是虚拟弹性系数,sgn(·)是符号函数.

为了方便计算,式(23)可以重写为

其中R表示绕旋转轴ra=(o −e)×v旋转π/2得到的旋转矩阵.相比Hoffmann等[20]只考虑了偏角φ的避障模型p(e,v)=Rv,本文算法耦合了偏角与距离的综合作用,避免了避障行为过早的缺陷.

对于多个障碍物的避障控制,可以叠加各个偏转加速度实现,即

式中:pm(e,v)表示存在多个障碍物情况下的避障加速度,下标i表示障碍物序号.综上,考虑到避障偏转,位置轨迹动力学系统式(7)可以重写为

3 系统稳定性分析

本章节将根据李雅普诺夫理论对所提算法的稳定性进行分析.由于算法中常数τ不影响轨迹的稳定性,这里设定τ=1.此外,当t →∞时,依赖于相变量的各项−K(gp −p0)x+Kfp(x)和−K2 log(go ∗)x+Kfo(x)趋近于0,在进行稳定性分析时不再考虑.

对于式(26)表示的位置轨迹动力学系统,根据单位质量线性弹簧系统的能量函数构建相应的李雅普诺夫能量函数V(p,v)

上式对时间进行求导,令式(26)中τ=1,将其代入可得

同理,对于式(11)描述的姿态轨迹动力学系统,依据单位转动惯量的线性扭簧系统能量函数构建相应的李雅普诺夫能量函数V(q,ω)

上式中,旋转矢量rg=2 loggo对应目标姿态,r=2 logq表示当前姿态,则当0,式(29)对时间进行求导,并将式(11)代入可得

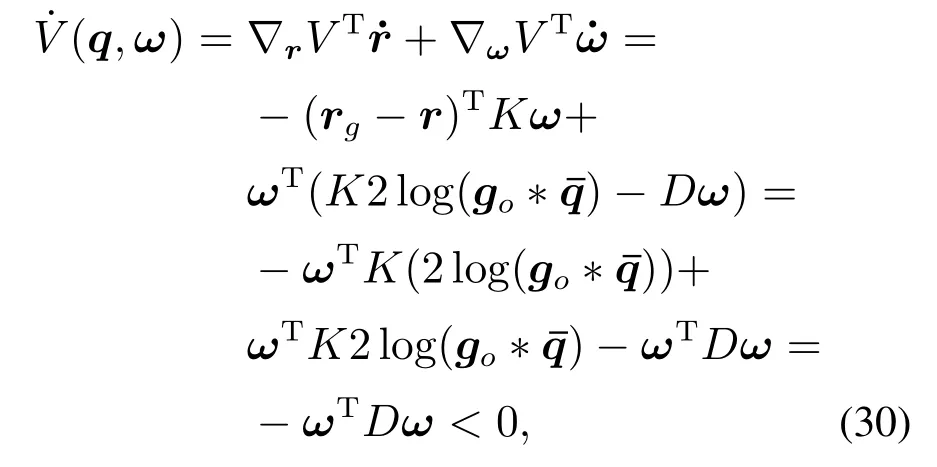
此外,当ω=0时,仿照位置部分的反证法,可得q=go.因此,姿态系统也是稳定的.

4 轨迹规划算法设计

在动态运动基元算法中,轨迹规划是在训练获得相应权值后,得到转换系统,然后依据任务需求的机械臂状态,利用转换系统计算新轨迹的过程.相应的流程如图2所示.由于姿态表示无法拆分的特殊性,模型中需要两套转换系统,分别保证位置上每个维度的运动与姿态的独立性.而整个运动的时间耦合特性则由同一个正则系统来保证,相关描述如图3所示.

图2 动态运动基元算法流程图Fig.2 The flow chart of dynamic movement primitives algorithm

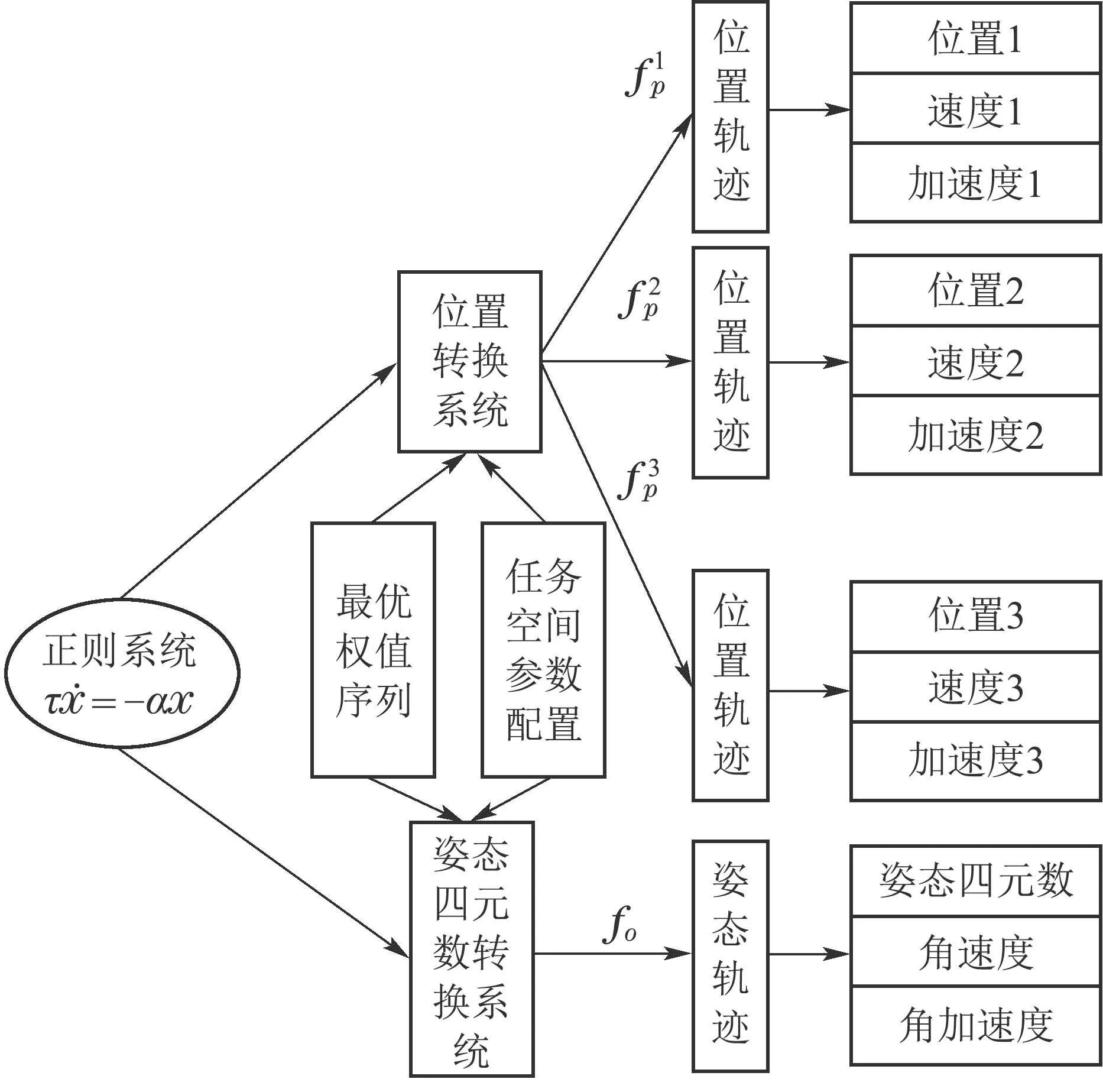
图3 6D轨迹算法原理图Fig.3 The principle diagram of 6D trajectories algorithm

在轨迹规划环节中,权值计算是其中的重要一环.Ijspeert等[14]针对标准一维DMP的强迫函数

通过局部加权回归的方式,将权值wi的计算表示为

上式中,s是空间缩放项与不同时刻相变量组成向量的乘积,Ψi是不同时间对应的径向基函数组成的对角矩阵,是由示教数据计算得到的强迫函数向量.

训练样本数据求得权值,得到转换系统后,依据新的状态,欧拉积分位置DMPs方程组就可以获得位置轨迹.而对于姿态轨迹,欧拉积分式(11)获得角速度,然后依据四元数的附加约束,利用四元数乘积计算(t+Δt)时刻对应的姿态,

由此,就可以规划生成期望的位置与姿态轨迹.

5 实验验证

为了对所提算法进行有效性验证,本文分别设计了6D轨迹的仿真实验、避障仿真实验和UR5的倒水实验.其中DMPs相关参数设定如下:弹性系数矩阵K设置为对角元素kii=576的3×3 对角矩阵,阻尼系数矩阵D设置为对角元素dii=48的3×3对角矩阵.径向基函数的数目n=125,相应的中心设置为ci=exp(−αi/(n −1)),带宽设置为hi=1/(ci+1−ci)2,hn−1=hn−2,i=0,1,···,n −1.正则系统中的常数项设置为α=2.避障模块中k=100,a=0.9,b=3,dmax=0.3.

5.1 仿真验证

通过本文的改进DMPs模型,可以规划生成6D位置和姿态轨迹,本章节设计了(a)起-终点状态相同、起-终点状态接近等跨零点情况下无避障机制的轨迹规划与(b)单障碍、多障碍避障的仿真实验进行相关验证.

在起-终点状态相同情况下,观察图4左侧可以发现,采用Ude等[21]的DMPs模型生成的轨迹数据(双划线)没有变化,而采用本文模型生成的轨迹(实线)基本与示教轨迹(虚线)重合,验证了所提算法在初始与目标状态差值项为0时的可行性.这主要得益于强迫函数与差值项成功解耦,避免了起-终点状态差值项等于0,强迫函数也等于0的情况,解决模型丧失学习能力的缺陷.

图4 起-终点相同/接近情况的轨迹Fig.4 The trajectories of the same/close initial-target point

在示教轨迹中起-终点状态非常接近的情况下,从相同起点出发,终点状态一个小的变化会导致状态差值项的急剧变化,可能导致轨迹规划失败,如图4中间和右侧所示.其中轨迹的起-终点状态偏差如表1所示,“同向”表示待规划轨迹的终点相对于起点的方向与示教轨迹相同,“反向”表示待规划轨迹的终点相对于起点的方向与示教轨迹相反.在图4中,Ude等[21]的DMPs模型获得的“同向”位置和姿态轨迹(双划线)相比示教轨迹(虚线)存在很大的波动,“反向”位置和姿态轨迹(双划线)相比示教轨迹(虚线)存在翻转的情况,但本文模型生成的“同向”与“反向”位置和姿态轨迹(实线)却能很好的跟踪示教轨迹,验证了起-终点状态差值项接近0时模型的有效性.这主要得益于强迫函数与差值项成功解耦,避免了起-终点状态差值项急剧变化对强迫函数的直接影响,消除了轨迹出现大幅度波动和翻转等情况.

表1 起-终点状态偏差Table 1 State deviation of initial-target points

在避障实验中,为了简化实验以及避开强迫函数的影响,选择动力学系统τ=K(gp −p)−Dz+.对于单个障碍物的避障控制,分别设计了3组实验,如图5中上图所示.在无障碍的情况下,从起点到终点是双划线表示的直线轨迹,但在双划线轨迹附近添加“*”表示的单个障碍物后,Hoffmann等[20]算法和本文算法轨迹都发生了偏转.对于多个障碍物的避障情况如图5中下图所示,与单个障碍物的情况类似,在3组轨迹平面添加了“*”表示的障碍后,轨迹很好的避过了所有障碍物.此外,相比Hoffmann等的避障算法,本文算法在接近障碍物时才开始偏转轨迹,从而避障总时间和轨迹总长度更短,这样有利于减少运动消耗.出现这种差别的原因是Hoffmann等的避障模型中直接检测偏角大小进行避障控制,忽视了机械臂和障碍物之间的距离,而本文避障算法机制中存在一个虚拟接触力估算模块,当机械臂和障碍物之间的距离较大时,虚拟接触力为0,避障因子也是0,轨迹不进行偏转.

图5 避障仿真实验结果Fig.5 Simulation experiment results of obstacle avoidance

此外,为了更好的体现本文避障算法相比Hoffmann等算法的优势,针对z=0平面内的单障碍和多障碍分别进行了100次测试.每次测试中随机生成1个障碍(x ∈(0,0.3),y ∈(0,1))和10个障碍(xi ∈(0,1),yi ∈(0,1),i=1,2,···,10),相应结果如表2所述.由于避障环节在某些情况下不连续,不方便统计避障开始时间和结束时间,在表2中不做记录.可以发现在100次测试中,对于单障碍,本文算法轨迹更短的概率为96%,时间更短的概率为81%.对于多障碍,本文算法轨迹更短的概率为100%,时间更短的概率为80%.即,本文避障算法避免了避障行为时间过长、轨迹过长问题,有利于减少运动消耗.

表2 Hoffmann等避障算法与本文避障算法仿真实验统计表Table 2 Simulation experiment statistics of Hoffmann’s obstacle avoidance algorithm and the proposed algorithm

5.2 UR5倒水实验

为了验证所提算法在真实机械臂上的有效性,本文在UR5机械臂上设计了倒水(以泡沫球代替水)实验,针对表3所述的轨迹初始与目标状态,分别验证其在原目标有无避障与新目标有无避障情况下轨迹的运行情况,结果如图6-7所示.其中障碍物位置估算是通过在障碍物表面粘贴ArUco码,利用视觉算法识别定位ArUco码实现的,而UR5机械臂的控制是在ROS框架下通过Socket通讯机制以C++编程实现的.在图6-7两图中,上图是无避障的轨迹测试,下图是带避障功能(乒乓球或泡沫圆柱)的轨迹测试,主要区别在于图7中目标状态对应的锅移到了实验台边缘.对比观察发现,在避障测试中位置轨迹发生了很大的偏移,而姿态轨迹没有发生偏移,这与模型期望是对应的,相关的位置轨迹、姿态轨迹和偏转加速度如图8-10所示.

表3 倒水实验初始/目标状态Table 3 Initial and target state of pouring-water experiment

图6 原目标运动示意图Fig.6 Diagram of movement to the original target

图7 新目标运动示意图Fig.7 Diagram of movement to the new target

图8 位置轨迹对比图Fig.8 Comparison chart of the position trajectories

观察图9可知,前5.7 s的时候,UR5完成从初始状态到图6-7中步骤3所示的倒水动作,停留2.7 s左右完成倒水,然后再回到步骤4所示的回正状态.整个过程中,机械臂的姿态轨迹发生了很大的变化,验证了姿态算法的泛化能力.在图9的局部放大图中,“原目标-无避障”轨迹是示教轨迹,“原目标-有避障”是存在障碍情况下算法对原目标的泛化轨迹,因此两者之间存在微小的偏差,而“新目标-无避障”和“新目标-有避障”都是算法对新目标的泛化轨迹,两者重合是因为避障算法不对姿态进行调整.此外,由于新目标与原目标的姿态差异小,所以4种情况下姿态轨迹差别不大.

图9 姿态轨迹对比图Fig.9 Comparison chart of orientation trajectories

观察图10可以发现,机械臂运动过程中,偏转加速度先增大后减少,在大概1.65 s时,偏转加速度达到了峰值,即此时UR5和障碍物间的距离-偏角产生的虚拟阻抗最大,因此避障模块生成最大的偏转加速度促使UR5迅速远离障碍物.

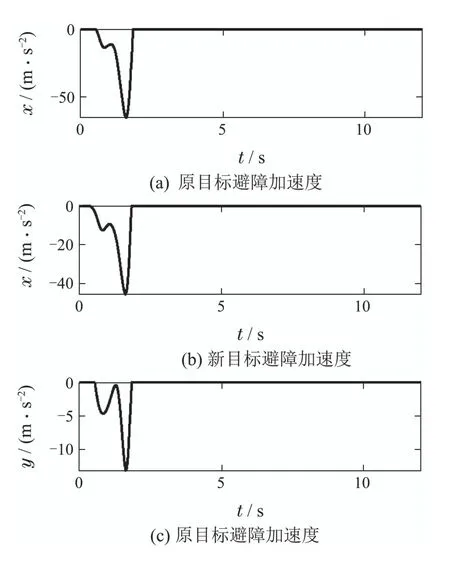
图10 避障加速度Fig.10 The accelerations of obstacle avoidance

6 结论

本文针对标准DMPs存在的问题,提出了适用于机械臂6D轨迹的DMPs算法,主要工作和创新点如下:

1) 采用四元数的方式编码姿态轨迹,实现姿态轨迹的无奇异表示.通过跨零点仿真实验,测试Ude等的DMPs对轨迹起-终点状态敏感性.最后引入Hoffmann等的序列化力场激励思想,改进了DMPs的转换系统,避免了算法在跨零点情况下的失败情况.

2) 基于虚拟阻抗的思想,设计了机械臂末端和障碍物之间的阻抗关系,综合考虑了两者之间距离和偏角的影响,实现了机械臂末端的避障控制,避免避障行为过早的缺陷,有利于减少运动消耗.

在本文中,机械臂的避障行为考虑的是末端避障,对于机械臂的整体避障,可以寻找机械臂各连杆与障碍物之间距离最近点M用于计算虚拟接触力,然后应用本文避障算法生成作用于M的偏转加速度,经过积分运算以及该最近点M对应的雅可比矩阵转换后,得到关节空间避障速度,方便与其他运动学系统整合.此外,运动技能的学习是通过一个动态运动基元序列实现的,对于复杂任务的学习泛化存在一定的局限性.因此,在未来的工作中,研究的重点是尝试建立多个动态运动基元序列库,依据实际情况拆分复杂任务,选择合适的动态运动基元序列去分别完成各个子任务.另外,后期也可以尝试将机械臂的柔顺控制以及感知模块加入本文模型,提升机械臂的性能.