基于强化健康指数相似度量的航空发动机失效阈值设置
刘小峰,史长振,黄洪升,柏 林
(重庆大学机械与运载工程学院,重庆 400044)
1 引言
航空发动机的剩余寿命预测(remaining useful life,RUL)对于保障发动机运行安全可靠,降低其维修成本具有重要的意义[1].鉴于航空发动机性能衰退物理模型的复杂性,利用运行状态监测数据构建健康指数(health index,HI)并采用智能网外推HI至失效阈值(failure threshold,FT),逐渐成为其RUL预测主流研究方法.
为了从航空发动机监测数据中构建能够表征其性能退化状态的HI,许多国内外研究学者通过特征的优化选择以单值原始物理监测量(如EGTM,DEGT等)作为发动机的HI[2-3],或者通过状态监测量的降维约简、加权融合、距离度量等方法得到发动机的综合HI[4-5].这些方法亦或对监测参量进行人工主观筛选,亦或在HI构建中未加入与RUL相关的约束条件,无法保证HI与RUL的相关性.随着机器学习技术的发展,基于智能学习网络的HI构建方法及其RUL预测模型得到了长足的发展,如Babu等[6]建立的基于深度卷积神经网络,Nieto等[7]提出的粒子群优化SVM,Martha A等[8]采用的贝叶斯层次模型,Yang等[9]开发的量子行为算法优化的极限学习机,彭开香等[10]提出深度置信网络与隐马尔科夫融合模型,Yuan等[11]采用的长短期记忆神经网络算法等.要指出的是,实际的航空发动机运行任务剖面多杂,工况环境多变,在测试发动机与训练发动机退化过程差异性较大的情况下,预测得到的RUL误差往往较大.
目前基于HI外推的RUL预测研究中采用的失效阈值,大多采用的是人工经验法[12-13]、失效阈值分布统计方法[13-14].前者根据主观经验设置,缺乏科学依据,后者需要以大量全寿命周期的衰退数据样本为支撑.Zhang等[15]通过相似性寿命预测方法对涡扇发动机仿真数据进行研究,预测结果远优于神经网络方法.曹惠玲等[16]通过相关分析提取与发动机性能衰退密切相关参数,提出了一种基于时间序列相似性匹配的航空发动机剩余寿命预测方法.张妍等[17]在特征相似性匹配基础上对航空发动机进行RUL进行了加权融合估计.上述这些方法大多采用特征序列间的欧式距离对发动机退化过程的进行相似估计,尚未涉及失效阈值的设置.另者,这种以序列距离匹配为基础的相似度量方法只考虑类序列的全局相似性,容易受到噪声干扰的影响,且没有考虑每个退化序列的个体差异性.
针对以上存在的问题,本论文结合Box-Cox变换、消噪自编码器(denoising autoencoder,DAE)及多重核典型相关(multiple kernel canonical correlation,MKCC)技术,强化了HI指数与飞行循环间的相关性;在充分考虑了发动机性能退化的个体差异性与相似性的情况下,引入了全阶时间幂灰色预测模型(gray forecasting model with full order time power terms,FOTPGM(1,1))及KL散度加权方法进行FT的设置.
2 航空发动机强化健康指数构建
2.1 监测物理量的Box-Cox变换
航空发动机监测的物理参数众多,如排气温度、燃料流量、旁路比率等,这些参数受环境工况、负载等影响随机性较大,规律性不强,对航空发动机性能退化的表征能力不强.为了增强监测参量与发动机RUL间的相关性,采用Box-Cox变换[18]强化传感器监测参数与发动机RUL间的相关性,使得变换后的参量与RUL具有较好相关性,同时增强参量之间的独立性.设航空发动机监测的物理参量集X包含N个样本,即X={x1,x2,···,xn,···,xN},每个样本中共有M个监测参量,即xn={xn1,xn2,···,xnm,···,xnM},xnm表示第n个飞行循环下的第m个监测参量幅值.X对应的飞行循环量为L={l1,l2,···,ln,···,lN},采用Box-Cox变换参数λ={λ1,λ2,···,λm,···,λM}得到变换后监测参量X(λ)=,其中:
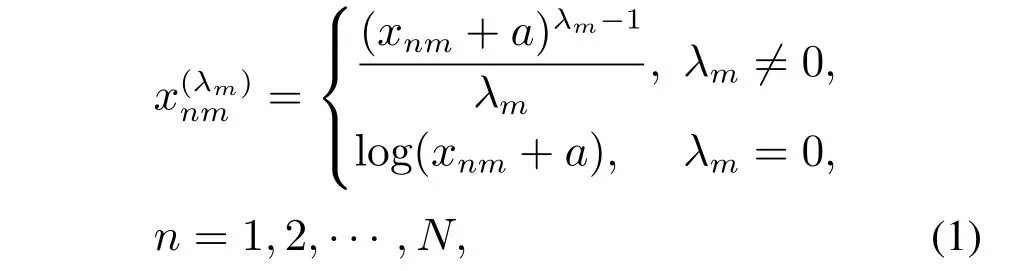
式中a为使监测参量X整体平移后大于0的常数.构造如式(2)中似然函数:

2.2 性能退化特征提取
航空发动机物理监测参量受环境工况、负载等影响存在较强的随机性,本文采用DAE弱化噪声及环境工况等不确定因素的影响的同时从航空发动机多维监测参量中提取深层次的退化状态信息.将经过Box-Cox变换后的航空发动机监测物理参量X(λ),随机加入噪声后记为,然后对进行编码,获得隐含层表示为[19]

式 中:D(·)为解码器的非线性转换,g(·)为和之间的映射函数;θD为解码器的参数.DAE网络通过最小化与X(λ)之间的重构误差实现网络的训练学习,得到的编码向量h={h(1),h(2),···,h(p)},p为编码向量的维度,即为输入样本对应的发动机退化特征表达.
2.3 基于多重核典型相关的HI构建
由于DAE提取退化特征时,并没有加入与发动机RUL相关的约束条件,无法保证提取的退化特征与RUL的相关性.因此,本文采用了多重核典型相关算法[20]对提取的退化特征进行强化处理,通过核函数学习一组相关投影方向,使不同退化特征投影到核空间后与发动机飞行循环数拥有最大的相关性,进而采用核空间的融合特征值作为发动机的强化健康指数.将H={h1,h2,···,hn,···,hN}∈Rp×N记为DAE提取的退化特征,对应的飞行循环数L={l1,l2,···,ln,···,lN}∈R1×N,将两者组合成(p+1)×N维的样本集合Y={Y(1),Y(2),···,Y(p+1)},每个子集的维度都为N.采用MKCC将p+1个子集映射到核空间得到:[Φ1,Φ2,···,Φp+1].多重核典型相关的目标函数为

3 自适应失效阈值设置
3.1 参考发动机FT预测
航空发动机的性能退化是由多因素引起的,每个因素对发动机RUL的影响是未知不确定的,其性能退化问题本身就存在于一个灰色系统中,本文采用的全阶时间幂灰色预测模型FOTP-GM(1,1)可以自适应地根据HI序列动态变化改变模型结构和参数,提高FT的拟合精度与发动机的RUL预测精度.
在FOTP-GM(1,1)模型[21]中,x(0)(k)满足

其中:a称为发展系数,bi(i=1,2,···,h)称为灰色作用量,h称为时间幂项bikh−i的阶数,h最大为4.x(0)(k)为k时刻的原始信号序列值;z(1)(k)为原始信号累加序列的紧邻均值生成序列值.采用最小二乘法,可估计出参数序列=(a,b1,b2,···,bh),根据式(7)即可求得FTOP-GM(1,1)模型的时间响应函数为
1.1.3 试验动物和细胞。SD大鼠,第四军医大学试验动物中心;黑色素瘤B16细胞株,中国科学院上海细胞生物研究所。
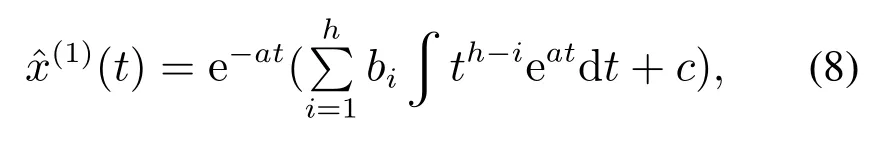
其中c为常数.为原始信号的累加序列.则x(0)(k)的FTOP-GM拟合值表示为

由于FOTP-GM(1,1)模型具有无差拟合近似非齐次指数序列的性能,采用FOTP-GM(1,1)模型对训练发动机的HI曲线进行拟合,能够有效避免HI曲线在最终寿命时间点上的端点畸变问题,从而降低FT设置偏差.全寿命参考发动机l的HI序列Hl(t),t=t1,t2,···,tl,在最终寿命时间点t=tl上的FTOP-GM(1,1)拟合值,即为该参考发动机的FT,即

3.2 基于KL距离HI相似匹配的FT加权设置
在参考发动机HI的基础上,如何确定测试发动机的FT是影响其RUL预测准确性的关键.由于各个发动机退化轨迹的差异性与相似性,本文采用基于KL距离寿命调节函数来综合确定测试发动机的失效阈值.计算待测发动机HI与各个全寿命参考发动机HI之间的KL距离并以此作为发动机退化轨迹相似度量指标,选取5个最小KL距离构造阈值调节函数,结合对应的5个全寿命发动机的FT,对测试发动机FT进行加权设置,即

其 中:l=1,2,···,5,KL(p(HItest)‖p(HIl))表示测试发动机的HI序列分布与训练发动机HI序列分布的KL距离,p(·)表示HI概率分布,ωl代表第l个发动机的失效阈值的加权系数.
3.3 基于HI外推的RUL预测
FOTP-GM(1,1)模型具有自适应的结构特征,其结构参数会根据发动机性能衰退演化趋势动态地自适应调节,不仅可以精确模拟齐次指数HI序列,而且可以无差模拟近似非齐次指数HI 序列,因此具有更高的预测精度,更强的泛化能力,更优的自适应性能.设测试发动机的历史HI曲线为HItest(l),l=l1,l2,···,lc,根据式(11)-(13)对其进行建模得到其对应的灰色模型FGMtest,则其RUL估计值为

4 基于强化HI阈值设置的发动机RUL预测
本文提出了基于强化HI相似度量的失效阈值设定方法,如图1所示.该方法主要步骤包括:1)采用Box-Cox算法对发动机监测物理量进行变换,增强其与飞行循环间的相关性;2)将Box-Cox变换后的物理参量输入DAE,提取发动机性能退化特征量;3)对DAE提取的退化特征量与对应飞行循环数进行MKCC运算,构建发动机强化HI指数;4)采用FOTP-G(1,1)模型对训练发动机的全寿命HI进行拟合,得到训练发动机的失效阈值;5)计算训练发动机的HI曲线与测试发动机的HI曲线的KL距离,在此基础上对训练发动机的FT进行加权平均,得到测试发动机的FT;6)采用FOTPG(1,1)模型对测试发动机HI进行外推至其设定的失效阈值,得到其RUL估计值.

图1 提出方法流程图Fig.1 Flowchart of proposed method
5 实验验证
5.1 数据描述
本文选用美国宇航局C-MAPSS航空发动机数据[20]对提出方法进行应用验证.该数据集共包括不同工况和失效模式的4组数据,每组数据包含3个工况参数和21个传感器监测参数.本文选取FD001数据集(即第一组)进行实验验证.该数据集包含100台全寿命训练数据、100台部分测试数据和测试数据对应的真实RUL.测试数中每台发动机的起始状态及观测序列长度均不同.关于发动机具体模块的信息以及传感器的说明详见文献[22].
5.2 监测参量强化处理
FD001数据集中,不同的监测物理参量有不同的退化趋势,在21个监测物理参量中,有7个监测参量在整个退化周期中幅值未发生变化,为了达到对发动机性能退化状态更准确的描述,剔除这7个监测参量,将剩余14个监测参量组成特征集.为改善传感器监测参数与发动机飞行循环序列之间的线性相关性,采用Box-Cox算法实现传感器监测参数的转换.以#2号发动机T50、P30、Nc、Ps30、BPR 5个传感器参数为例,参数λ取值范围为[−5,5],通过最大似然估计法计算所得Box-Cox变换参数λ最优值以及变换前后各传感器参数与飞行循环序列的Pearson系数对比如下表1所示.从表中可以看出,经过Box-Cox变换后,表中所展示的5个传感器参数与飞行循环之间的线性相关度均得到了一定程度的提升.

表1 Box-Cox变换前后Pearson系数对比表Table 1 Comparison of Pearson coefficient before and after Box-Cox transformation
5.3 建立健康指标
DAE网络参数设置为:输入层节点个数为14,第1层隐含层节点数为10,第2层隐含层节点数为5,学习率为0.001.按照式(3)-(6)对DAE网络进行训练,得到维度为5的退化特征向量,再采用MKCC得到的强化HI曲线.图2给出了#40,#56,#78,#88号训练发动机的HI曲线,可以看出采用本文方法提取的发动机HI曲线退化趋势明显,波动幅度小,前期HI变化幅度不大,说明发动机属于正常状态,而后期HI下降明显,说明发动机进入衰退状态.

图2 训练发动机的强化HI曲线Fig.2 Enhanced health index of training aero-engines
图3给出了直接采用DAE算法构建的HI曲线,相较于图2,HI曲线的波动性明显增大,本文构建的强化HI更大程度上摈除了噪声的干扰,能更有效地表征发动机性能退化过程.

图3 基于DAE算法的训练发动机HI图Fig.3 Health index of training aero-engines based on DAE algorithm
5.4 失效阈值确定
以FD001中的#43,#72,#87,#99号测试发动机为分析对象,对100个全寿命参考发动机的HI指数曲线进行KL距离匹配,得到5个KL距离最小的参考发动机如表3所示.对这5个全寿命发动机的HI进行FOTPGM(1,1)模型拟合后,得到最后失效点对应的FT值,继而按照式(11)-(12)计算得到#43,#72,#87,#99号测试发动机的失效阈值,结果如表2所示.

表2 测试发动机失效阈值Table 2 FT of test aero-engines
5.5 RUL预测
在测试发动机HI曲线与设定阈值的基础上,采用FOTP-GM(1,1)模型方法进行测试航空发动机的剩余寿命预测.部分测试发动机剩余寿命预测结果如图4所示,具体预测结果数值由下表3给出.图4(a)与(b)依次为#43,#72号测试发动机剩余寿命预测图,其真实RUL与预测RUL之间的飞行循环次数误差分别为3和4.由此可见,对于当前飞行循环次数较多的测试发动机由于具有足够的历史监测数据,FOTP-GM(1,1)可以较准确地获得其剩余寿命.图4(c)与(d)分别是#87,#99号测试发动机剩余寿命预测图,其真实RUL与预测RUL的误差为11和9个飞行循环.可见,飞行次数少的测试发动机由于历史数据较缺乏,FOTP-GM(1,1)模型获得的预测精度尽管有所降低,但仍在可接受范围之内.因此FOTP-GM(1,1)同样适合于短数据的长时间预测.
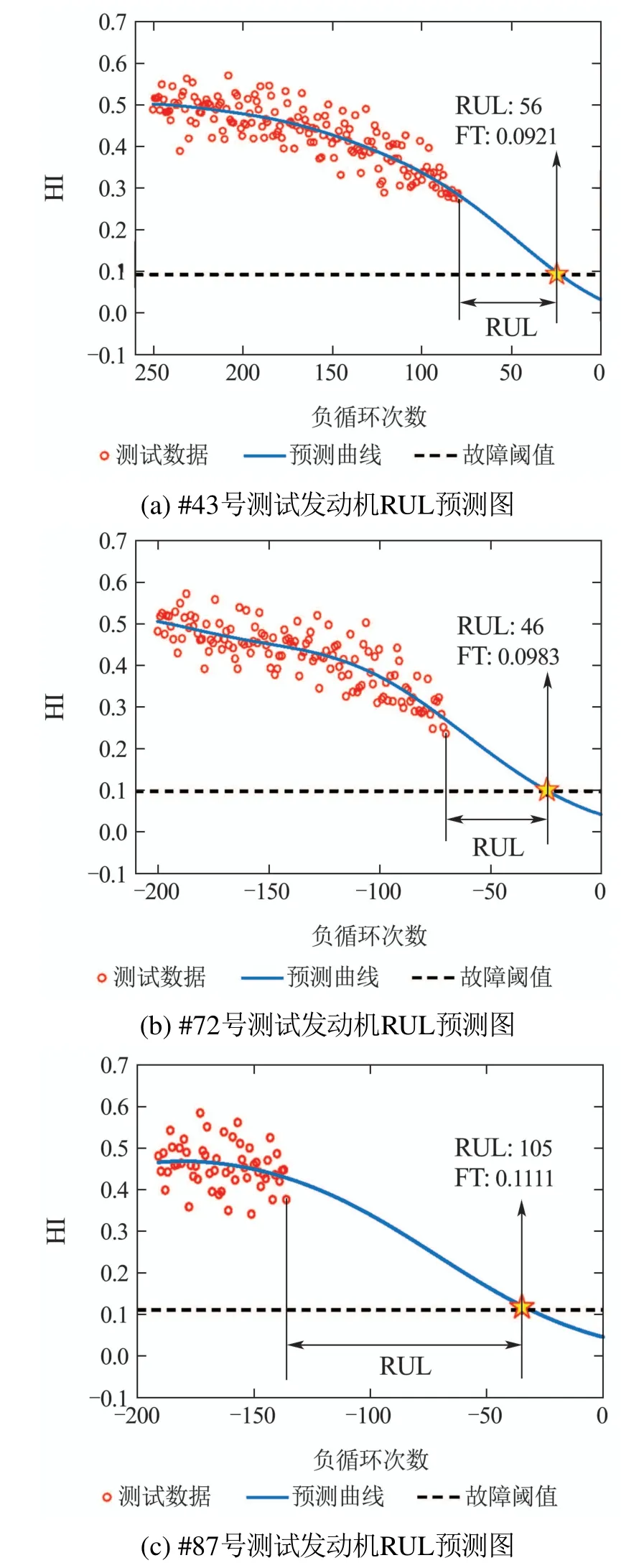

图4 测试发动机RUL预测图Fig.4 RUL prediction for test aero-engines

表3 部分测试发动机RUL预测结果Table 3 RUL prediction results of some test aeroengines
5.6 RUL预测结果比较分析
图5(a)给出了100个测试发动机的RUL预测结果与真实RUL的对比分析图,可见,各个测试发动机的预测误差都各有不同,最小误差为0,最大误差为41个飞行循环,这主要和各个测试对象的历史数据长短,波动程度及退化轨迹各异有关.图5(b)给出了测试RUL误差(预测RUL减去真实RUL)的分布情况,76%的测试发动机RUL预测误差集中在−13至10个飞行循环且提前预测数量远多于滞后预测,符合工程实际要求,验证了本文提出方法的准确性.

图5 100个测试发动机RUL预测误差图Fig.5 RUL prediction error for 100 test aero-engines
为了进一步验证本文预测方法的优势,采用Score指标对预测结果进行量化评价,并与卷积神经网络(CNN)算法[6]和极限学习机模糊聚类(EML-FC)算法[23]预测RUL所得Score指标进行对比.Score指标[23]计算公式如下:
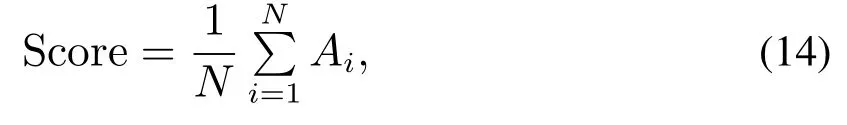

式中:actRULi,preRULi,Ei和Ai分别是第i个测试发动机的实际剩余寿命、模型预测寿命、误差率和得分;Score代表N个测试发动机的平均得分,这里N=100.从式(14)-(15)可以看出,Ai与Score越小,说明预测出的RUL精度越高,方法性能更加稳定.经计算,本文方法预测得到的Score值为346,小于EML-FC方法的Score得分1046,CNN方法的得分1287.可见,本文方法对100个发动机RUL预测的平均精度大于传统方法,该方法通过强化HI的失效阈值自适应设置,提高了发动机RUL预测精度与可信度.
6 结论
本文针对航空发动机监测物理参量对发动机退化状态表征能力不强的问题,利用Box-Cox变换、DAE以及MKCC算法,强化了发动机HI与其飞行循环数的相关性,并采用了基于KL距离的HI相似度量法对其FT进行了自适应设置.试验结果表明,本文提出的FT设置方法,充分考虑了不同发动机退化模式相似性与差异性,降低了阈值主观设置造成的RUL预测的不确定性,提高了RUL的预测精度,在航空装备寿命预测领域具有较好的应用前景.

