关于“分数乘分数”的深度思考

张春梅

（涉县第二实验小学，河北 邯郸 056400）

分数乘法是人教版六年级的内容，每年在教学这部分内容时，总要遭遇分数乘分数这块难啃的“骨头”。大家一致认为，分数乘分数的计算法则是容易掌握的。最棘手的问题是，如何让学生在学会计算的同时更好地理解分数乘分数的意义，因为这对后续分数应用题的学习具有重要的意义。

基于以上一系列思考，本设计主要通过两个环节开展教学活动，一是让学生理解分数乘分数的意义；二是在理解意义基础上推导计算法则。

一、激发认知冲突，拓展乘法意义

（一）比较

学生在过去分数乘整数的基础上，很快画图列出算式：

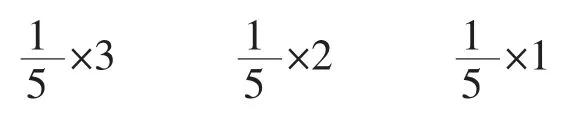
师：你能说出每个算式的含义吗？

学生结合图示说出每个算式表示的含义。

师：为什么这样列式？能说一下理由吗？

生2：根据“工作效率×工作时间=工作总量”，可以列出算式。

生3：1 小时就相当于1 份，3 小时就是3份，所以用乘法计算。

师：这些算式有什么相同之处呢？

生：都是求一个数的几倍是多少。

设计说明：此处教师让学生寻找三个问题的共同之处，唤醒旧知，明确分数乘整数的意义，为下面迁移类推拓展乘法的意义做好充分准备。此环节的展开还是比较顺利的，因为学生有过去整数乘法做基础。

（二）建构

教师接着出示问题并提出要求：

A.采取自己喜欢的方式解决问题，比如画图。

B.解释算理。

学生列出算式，交流列式根据。

生1：根据“工作效率×工作时间=工作总量”，直接列出算式。

生2：1 小时刷的面积知道了，那么不管几小时都用乘法计算。

师：请同学们结合一位同学画的图，思考一下，这三个算式表示什么意义？学生在辨析讨论中遇到困难，教师引导：

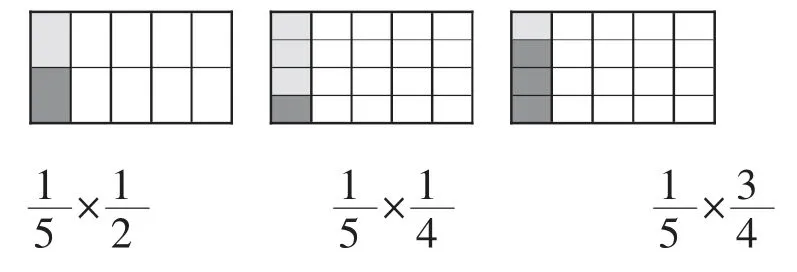
师：我们把这三个图与刚才第一组的第三个图比较一下，你发现了什么？

生1：从图上可以知道，第一组的第三个图表示1 小时刷整个墙的，那么小时刷的就是这个的

师：回过头来看我们列出的算式，还是原来的求几个几的意义吗？

设计说明：此环节教师抛出今天研究的新问题，借助画图的方式帮助理解和列出算式，在利用旧知无法解释新问题时，学生一般会打破心理平衡，产生认知冲突，即皮亚杰提出的顺应现象。此时，教师引导学生认真观察图示，从图示中寻求算式的意义，学生很快发现乘一个分数就是求这个数的几分之几这样的关系。

（三）提升

师：将前三个问题归为第一组，后三个问题归为第二组，这两组问题有什么相同和不同之处吗？请大家小组讨论交流一下。

师：也就是说，当我们求一个数的几倍的时候用乘法，当我们求一个数的几分之几的时候也可以用乘法，对吗？下面我们再重新来看看刚才出示的所有图示和算式：

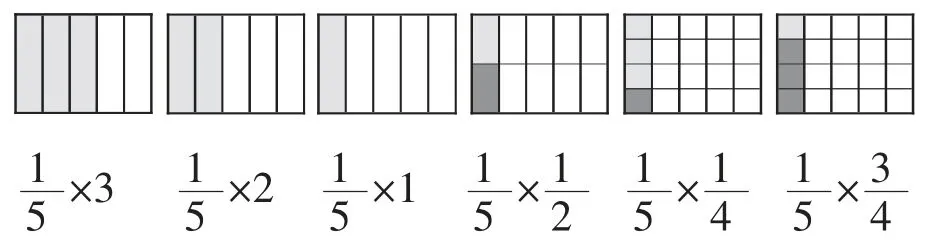
设计说明：从相同点可以统一概括乘法的意义，突显新知与旧知之联系；从不同点使学生明确整数乘法与一个数乘分数的意义有所不同，冲破过去乘法的理解限制，突显新知之“新”在何处，旧知与新知关系清晰，此时学生的小学乘法意义结构已初步构成。

二、利用数形结合，推导计算法则

（一）方法发现

师：刚才我们理解了算式的意义，那么你知道第二组的算式等于多少吗？

学生很快找出答案。

师：观察图示和算式的结果，你发现了什么？为什么会这样？

学生发现了用分数的分子乘分子得出积的分子，分母乘分母得出积的分母。

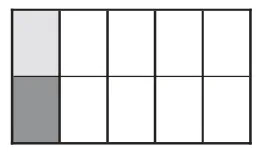
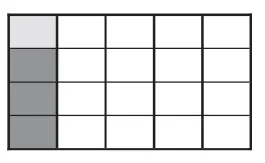
（二）专项练习

A.请你根据下面的图示列出算式，并写出计算过程。

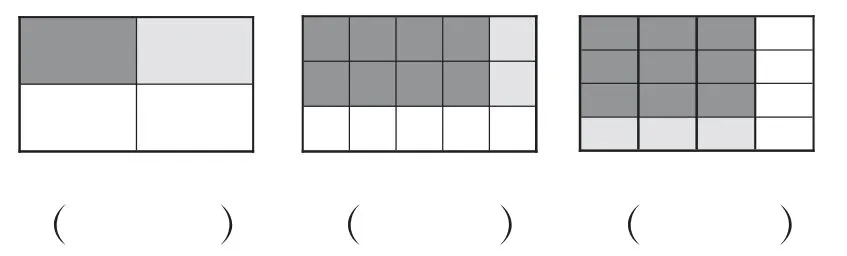
B.计算下面各题

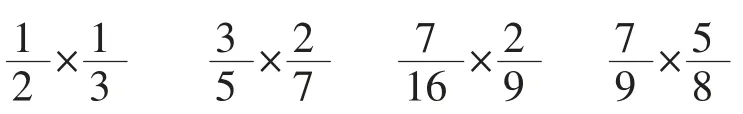
C.通过画图的方法解释B 题中的任意一个算式意义和算理。

设计说明：学生虽然能够从图上得出算式的答案，但不代表已经通晓算理。教师没有简单地停留在计算技能的训练上，而是引导学生思考计算过程的道理，采取的方法就是结合图示对应理解。同时，为了摆脱例题图示的影响，出示三道练习题，进一步加深对算式的意义和算理的理解；一方面拓展图示的份数，另一方面由图示过渡到单独的算式，最后再由算式尝试解释，这样的过程有效地建构起分数乘分数的计算法则。

【教学反思】

1.从整数到分数，实现乘法意义的拓展。如果教师直接按照教材呈现新知，势必会使学生陷入多重问题之中：一个分数的几分之几如何理解，为什么用乘法计算，乘法的意义如何建构等等。不仅意义理解不到位，计算法则也会流于技能层面。俗话说，“接知如接枝”，新的知识总是在原有知识的基础上发展而成的。以上设计从学生的已有知识经验出发，根据过去整数乘法意义的理解，先从3 小时、2 小时、1 小时开始，然后逐步拓展到小时、小时、小时等，由整数的几倍过渡到一个整体及到这个整体的一部分，使学生遭遇认知冲突，继而上升到对一个数的几分之几的认识，实现了乘法意义的有效拓展。美国著名教育家布鲁姆明确提出，不论我们选教什么学科，务必使学生理解该学科的基本结构。本节课中乘法意义的知识结构就显得清晰连贯，有效沟通了新知与旧知之间的密切联系，取得了较好的教学效果。

2.从图形到算式，突破学生学习的难点。本设计无论是分数乘法意义的建构还是计算法则的推导均采用了画图理解的方式，使得学习难点得到了有效突破。首先，在意义理解上，的几倍和的几分之几通过表格表示，给学生提供一个十分清晰的表象，为抽象意义准备了充分的感知材料。其次，在计算法则的推导上，每步计算都能在图形中得到解释和意义支撑，使得法则的形成顺理成章，有效突破了学习难点。曹培英教授指出，这种表格图示就是分数乘法的几何模型，为什么分母相乘、分子相乘，一目了然，可以很好地培养学生的几何直观能力。