一种改进的特征子集区分度评价准则

谢娟英 吴肇中 郑清泉 王明钊 ,2

大数据时代的数据不仅样本量剧增,维数也日益剧增,引发维数灾难[1],增加计算复杂度,而且冗余和不相关特征使得分类器性能较差,给数据分析带来挑战.因此,特征选择及其评价成为一个研究热点[2−6].

特征选择旨在发现具有强分类能力且互不相关或尽可能互不相关的少量特征构成特征子集.特征搜索策略包括完全搜索、随机搜索和启发式搜索3大类[7].特征选择算法可分为:Filter[8],Wrapper[9],Embedded[10],Hybrid[11−13],以及Ensemble[14]几大类.Filter 方法根据独立于分类器的特征重要性评价准则,如卡方检验等来判断特征的分类能力,选择分类性能强的特征构成特征子集.Filter 方法独立于学习过程,速度快,但需要阈值作为停止准则,且准确率较低.Wrapper 方法依赖于分类器,需要将训练样本分为训练子集和验证子集两部分,特征选择则过程中,以分类器在验证子集的性能判断相应特征子集的分类能力,选择分类能力强的特征子集.构建基于特征子集的分类模型,以测试集对模型进行评价,从而评价特征子集和相应特征选择算法的性能.Wrapper 方法中,特征选择过程中使用的学习算法完全是一个 “黑匣子”.因此,Wrapper方法依赖于学习过程,准确率较高,但计算量大,且存在过适应风险.Embedded 方法通过优化一个目标函数实现特征选择,特征选择在优化目标函数过程中完成,不需要将训练样本分成训练子集和验证子集,但构造合适的优化目标函数困难.Hybrid 方法集成Filter 方法和Wrapper 方法的优势,采用Filter 方法独立于分类器的准则度量特征分类能力大小,以一定的启发式策略来搜索特征子集,采用Wrapper 方法的以分类器分类性能评价相应特征子集的分类能力.因此,Hybrid 方法得到广泛关注.Ensemble 方法集成不同特征选择算法实现特征选择,一般情况下具有较好性能,能选择到分类能力较好的特征子集,但需要训练多个不同分类器.

Relief 算法[15]是经典的Filter 方法,但只适用于二分类问题.Relief-F[16]算法将Relief 由二分类扩展到多分类问题.LVW (Las Vegas wrapper)算法[17]在拉斯维加斯方法(Las Vegas method)框架下使用随机搜索策略实现特征选择.SVM-RFE(SVM-recursive feature elimination)[18]基于SVM(Support vector machine)和后向剔除思想实现特征选择,是经典的Embedded 特征选择算法,是为解决超高维基因选择问题提出的算法,但若每次只剔除一个基因,时间消耗将成为瓶颈.为此,作者Guyon 指出,对于超高维基因选择,每次迭代,可一次剔除上百个基因,但她没有给出到底一次剔除多少个基因合适的理论依据和实践指导.mRMR(Max-relevance,min-redundancy)[19]基于特征相关性,旨在选择到分类能力强且冗余度最小的特征构成特征子集,但不同的相关性度量可能会得到不同的结果.F-score[20]是衡量特征在两类间分辨能力的有效准则.Xie 等将F-score 推广用于任意类分类问题[13,21],并提出考虑特征测量量纲的改进F-score 特征重要度评价准则D-score[22],用于皮肤病诊断.针对F-score 和D-score 仅考虑单个特征区分能力,没有考虑特征联合贡献的问题,谢等提出了考虑特征联合贡献的特征子集区分度衡量准则DFS (Discernibility of feature subsets)[23],从而获得分类能力更优的特征子集.LLE Score (Locally linear embedding score)[24]算法通过局部线性嵌入,实现非线性维约简[25],进行肿瘤基因选择.AVC (Feature selection with AUC-based variable complementarity)算法[26]通过最大化变量互补性实现特征选择.最大化ROC 曲线下面积的基因选择算法[27]实现了非平衡基因数据的特征选择.特征选择算法DRJMIM (Dynamic relevance and joint mutual information maximization)[28]充分考虑特征相关性和特征相互依赖性,采用动态相关性和最大化联合互信息实现特征选择.基于邻域粗糙集的特征选择算法[29]基于邻域熵的不确定性度量,从基因表达数据集中选择差异表达基因实现癌症分类.谢等对非平衡基因数据的差异表达基因选择进行了系统研究[30],提出了16 种针对非平衡基因数据的特征选择算法.Li 等[31]从数据视图角度对特征选择算法进行总结,将特征选择算法分为基于相似度的方法、基于信息论的方法、基于稀疏学习的方法,以及基于统计的方法4 大类.

特征选择研究已引起研究者广泛关注,是高维小样本癌症基因数据分析的首要步骤,也是其他高维数据分析的基础.然而,现有特征选择算法对特征分类能力的评价,多数仅考虑单个特征的分类贡献,并忽略了特征测量量纲的影响,DFS[23]准则考虑了特征的联合贡献,但其没有考虑不同测量量纲对特征分类贡献的影响,值域差异悬殊的特征,相当于被赋予了差异悬殊的权重,无法准确度量特征对分类的贡献量.为此,提出GDFS (Generalized discernibility of feature subsets)新准则,引入离散系数对DFS 准则进行改进,客观度量特征子集的分类能力.以ELM (Extreme learning machine)为分类工具评估特征子集的分类性能.UCI (University of California in Irvine)机器学习数据库数据集和基因数据集的实验测试,以及与DFS和现有经典特征选择算法的实验比较与统计显著性检测表明,提出的GDFS 特征子集区分度评价准则是一种有效的特征子集分类能力度量准则,能选择到分类性能很好的特征子集.

1 GDFS 特征子集区分度

设数据集X包含l(l ≥2)个 类,第c(c=1,···,l)类样本数为nc.

1.1 DFS 特征子集区分度

DFS 特征子集区分度衡量准则[23]考虑特征子集所包含特征的联合作用,评价特征子集的类别间区分能力大小.则含有i个特征的特征子集的区分度DFS 定义为式(1).

1.2 GDFS 特征子集区分度

离散系数(变异系数)是样本标准差与样本均值之比,消除了特征测量量纲对度量样本离散程度的标准差大小的影响,离散系数越大表明数据离散程度越大,反之越小[32].

DFS 没有考虑特征测量量纲对特征重要度的影响,不同特征取值范围差异悬殊情况下,相当于对取值较大特征赋予了较大权重,使其容易被选择到,从而影响特征选择结果的客观性.为了客观度量每个特征的分类能力,避免特征测量量纲不同带来的影响,提出GDFS 特征子集区分能力度量准则,克服DFS 的缺陷,以便发现真正具有区分能力的特征.GDFS 定义为式(2).

式(2)中分子表示l个类别对应当前i个特征的类别间离散系数,其值越大,表示各类别间的分散程度越好;分母表示l个类别对应当前i个特征的类内离散系数之和,其值越小,表示各类别越紧凑.因此,式(2)的值越大,表明当前i个特征构成的特征子集的分类能力越强.

1.3 GDFS 正确性理论分析

GDFS 针对DFS 没有考虑特征测度对特征区分能力影响的缺陷提出采用离散系数对DFS 进行改进,因此,若能证明离散系数不受测度影响,而标准差受测度影响,则可证明GDFS 正确.为此,提出下面的定理,并进行理论证明.

2 极限学习机

极限学习机ELM 是基于单隐层前馈神经网络的机器学习算法[33].ELM 随机产生输入层和隐藏层之间的连接权重和隐藏层阈值,只需要设定隐藏层结点数便能获得唯一最优的隐藏层到输出层的连接权重.

假设有N个训练样本对 (xi,ti),xi ∈Rn,ti ∈Rm,激活函数为g(·),则有个隐结点的单隐层前馈神经网络的数学模型描述为式(3).

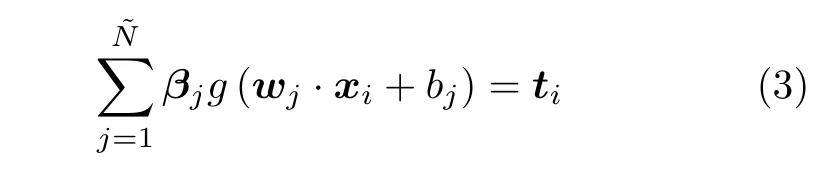
其中,wj表示第j个隐结点和所有输入结点间的权重向量,βj表示第j个隐结点和所有输出结点间的权重向量,bj是第j个隐结点的阈值.

带有个隐结点的ELM,激活函数g(·) 能够以零误差逼近N个训练样本,即存在βj,wj,bj,使式(3)成立.式(3)可简写为式(4)矩阵形式.

3 基于GDFS 的特征选择算法

假设S为包含n个特征的特征全集,C是选择的特征子集,C初始化为空集,划分数据集为训练集和测试集,在训练集进行特征选择,采用SFS,SBS,SFFS 和SBFS 特征搜索策略,以GDFS 评价特征子集性能,得到算法1～4 描述的4 种混合特征选择算法:GDFS+SFS,GDFS+SBS,GDFS+SFFS,GDFS+SBFS.

算法1.GDFS+SFS 特征选择算法

4 实验结果与分析

为了避免实验结果受不同数据集划分的影响,采用5-折交叉验证实验,以获得平均的实验结果.并在实验前,随机打乱样本获得随机实验数据.打乱方法为:随机生成一个足够大2 维数组,数组元素的取值为1～数据集规模之间的一个随机数,交换数组每行两个元素值对应样本.

4.1 ELM 与SVM 性能比较

本小节采用DFS 特征子集评价准则,结合SFS,SBS,SFFS 和SBFS 特征搜索策略,分别采用ELM 和SVM 分类工具引导特征选择过程,比较基于相应特征子集的ELM 和SVM 分类器的性能,选择分类性能好的分类器.实验采用UCI 机器学习数据库[34]的iris,thyroid-disease,glass,wine,Heart Disease,WDBC (Wisconsin diagnostic breast cancer),WPBC (Wisconsin prognostic breast cancer),dermatology,ionosphere 和Handwrite 数据集.数据集描述见表1.thyroid-disease 是thyroid gland data 数据集;Heart Disease 为processed Cleveland,删掉6个含有缺失数据的样本,样本数由303 变为297;WPBC 删掉了4个含有缺失数据的样本,样本数由198 变为194;dermatology 删掉了8个含有缺失数据的样本,因此样本数由366 变为358;Handwrite 选择了前2类进行实验.

表1 实验用UCI 数据集描述Table 1 Descriptions of datasets from UCI

SVM 分类器采用林智仁等[35]开发的SVM 工具箱,核函数采用RBF (Radial basis function)核函数[36],参数采用默认值.ELM 采用RBF 核函数,参数为默认值,隐藏层结点数以5 为步长增加,根据交叉验证结果选择最优隐结点数[33].为避免ELM 的随机初始输入权重向量和隐结点阈值影响实验结果,实验中设定阈值为0.01,当训练数据集的分类正确率在一定范围内波动时,认为分类正确.图1～4 展示了分别采用ELM 与SVM 为分类器,以DFS 度量特征子集性能的5-折交叉验证实验平均结果.

图1 实验结果显示:采用SFS 搜索策略,以ELM 分类器引导特征选择过程得到的特征子集不仅规模小,且在绝大部分数据集上的分类性能更好.图2～图3 实验结果显示,采用SBS 和SFFS 搜索策略,以ELM 或SVM 为分类器,除了Handwrite数据集,其他数据集的特征数量差别不大,但ELM分类器得到的特征子集分类能力更强.图4 的实验结果显示:ELM 分类器选择的特征子集的规模在多数数据集上比SVM 得到的特征子集规模稍大,但ELM 分类器得到的特征子集的分类性能优于SVM 选择的特征子集的分类性能.

图1 DFS+SFS 算法的5-折交叉验证实验结果Fig.1 The 5-fold cross-validation experimental results of DFS+SFS

图2 DFS+SBS 算法的5-折交叉验证实验结果Fig.2 The 5-fold cross-validation experimental results of DFS+SBS

图3 DFS+SFFS 算法的5-折交叉验证实验结果Fig.3 The 5-fold cross-validation experimental results of DFS+SFFS

特征选择的目标是:发现规模小且分类性能好的特征子集.综合图2～图4 的实验结果可见,采用ELM 分类器能够获得分类能力更好的特征子集.

图4 DFS+SBFS 算法的5-折交叉验证实验结果Fig.4 The 5-fold cross-validation experimental results of DFS+SBFS

4.2 GDFS 与DFS 性能比较

本小节在第4.1 节实验基础上,选择使DFS 性能更优的ELM 分类器,测试提出的GDFS 特征子集性能评价准则的优越性.提出的4 种特征选择算法GDFS+SFS,GDFS+SBS,GDFS+SFFS,GDFS+SBFS 与原DFS+SFS,DFS+SBS,DFS+SFFS,DFS+SBFS 在表1 数据集的5-折交叉验证的实验结果如表2～表5 所示,加粗和加下划线表示最优实验结果.

表2～表5 的5-折交叉验证实验结果显示:GDFS+SFS,GDFS+SBS,GDFS+SFFS 和GDFS+SBFS 选择的特征子集的分类能力均分别优于DFS+SFS,DFS+SBS,DFS+SFFS 和DFS+SBFS 算法选择的特征子集的分类能力.因此,GDFS 比DFS选择的特征子集的分类能力更强.从各算法选择的特征子集规模来看,GDFS+SFS 选择的特征子集规模最小,接着是GDFS+SFFS 和GDFS+SBFS算法,GDFS+SBS 算法选择的特征子集规模较大.另外,GDFS+SFS,GDFS+SBS,GDFS+SBFS 比DFS+SFS,DFS+SBS,DFS+SBFS 选择的特征子集规模平均值略小,GDFS+SFFS 与DFS+SFFS选择的特征子集规模基本相当,前者略大一点.

表2～表5 的5-折交叉验证实验结果还显示,GDFS+SFFS 算法选择的特征子集的分类性能最好,GDFS+SFS 和GDFS+SBS 选择的特征子集的分类能力相当,不如GDFS+SFFS,但优于GDFS+SBFS 算法选择的特征子集的分类能力.

2.7 图表 每幅图单独占1页，集中附于文后，表格随正文附出。图表应按其在正文中出现的先后次序连续编码，并应冠有图(表)题。说明性的资料应置于图(表)下方注释中，并在注释中标明图表中使用的全部非共知共用的缩写。本刊采用三横线表(顶线、表头线、底线)，如遇有合计或统计学处理行(如t值、P值等)，则在此行上面加一条分界横线;表内数据要求同一指标有效位数一致，一般按标准差的1/3确定有效位数。线条图应墨绘在白纸上，高宽比例为5∶7左右。计算机绘制图者应提供激光打印图样。凡能使用文字表达清楚的内容，尽量不用表和图，如使用表和图，则文中不必重复其数据，只需摘述其主要内容。

表2 GDFS+SFS 与DFS+SFS 算法的5-折交叉验证实验结果Table 2 The 5-fold cross-validation experimental results of GDFS+SFS and DFS+SFS algorithms

表3 GDFS+SBS 与DFS+SBS 算法的5-折交叉验证实验结果Table 3 The 5-fold cross-validation experimental results of GDFS+SBS and DFS+SBS algorithms

表4 GDFS+SFFS 与DFS+SFFS 算法的5-折交叉验证实验结果Table 4 The 5-fold cross-validation experimental results of GDFS+SFFS and DFS+SFFS algorithms

表5 GDFS+SBFS 与DFS+SBFS 算法的5-折交叉验证实验结果Table 5 The 5-fold cross-validation experimental results of GDFS+SBFS and DFS+SBFS algorithms

综上分析可见,提出的GDFS 比原始DFS 更优,能选择到分类能力好且规模较小的特征子集.其中,GDFS+SFFS 算法选择的特征子集分类能力最优,且规模较小.因此后面对比实验中仅选择GDFS+SFFS 算法与现有经典算法进行比较.

4.3 GDFS 与其他特征选择算法的比较

本小节用6个经典基因数据集Colon[37]、Prostate[38]、Myeloma[39]、Gas2[40−41]、SRBCT[42]和Carcinoma[31]进一步测试提出的特征子集性能评价准则GDFS 的优越性.数据集详细信息见表6.实验将比较提出的GDFS+SFFS 与现有特征选择算法DFS+SFFS[23],Relief[15−16],DRJMIM[28],mRMR[19],LLE Score[24],AVC[26],SVM-RFE[18],VMInaive(Variational mutual information)[43],AMID (AUC and mutual information difference)[30],AMIDDWSFS (Dynamic weighted SFS using dynamic AUC and mutual information difference)[30],CFR(Composition of feature relevancy)[44],FSSC-SD(Feature selection by spectral clustering based on standard deviation)[45]选择的特征子集的ELM 分类器的分类准确率Accuracy、查准率precision、查全率recall、查准率和查全率的调和平均F-measure、正负类查准率的调和平均F2-measure[30],ROC(Receiver operating characteristic)曲线下面积AUC (Area under and ROC curve)[46−48].

由于基因数据集所含特征数成千上万,为了减少各特征选择算法的运行时间开销,实验首先采用D-score 算法[22]对表6 数据集进行特征预选择,剔除部分不相关和冗余特征,得到各数据集的候选特征子集,各算法在候选特征子集上进行特征选择.表7 展示了GDFS+SFFS 与特征选择算法DFS+SFFS、Relief、DRJMIM、mRMR、LLE Score、AVC、SVM-RFE、VMInaive、AMID、AMIDDWSFS、CFR 及FSSC-SD 的5-折交叉验证实验结果,加粗和下划线表示最优结果.对比算法的参数设置为:Relief 算法的最近邻数为3;LLE Score算法的类内邻域为4,类外邻域为12;AVC 算法的preSelePara 参数为默认值.

表6 实验使用的基因数据集描述Table 6 Descriptions of gene datasets using in experiments

表7 各算法选择的特征子集的ELM 分类器的Accuracy、AUC、recall、precision、F-measure 和F2-measure 实验结果显示,提出的GDFS+SFFS算法所选特征子集的分类能力除了在Prostate 数据集的AUC、在Gas2 的recall、在Carcinoma 的F2-measure 略低于DFS+SFFS 算法外,在该3个数据集的其他5个评价指标,以及在其他3个基因数据集的6个评价指标Accuracy、AUC、recall、precision、F-measure 和F2-measure 均优于原始DFS+SFFS 算法.从特征子集规模来看,提出的GDFS+SFFS 算法除了在Carcinoma 数据集的特征子集规模略高于(即选择的特征数稍多于) DFS+SFFS 算法外,在其他数据集得到的特征子集的规模(特征数)都不高于DFS+SFFS.因此,可以说提出的特征子集区分度评价准则GDFS 优于原始DFS,能选择到规模较小且分类能力强的特征子集.

另外,提出的GDFS+SFFS 算法所选特征子集的ELM 分类器的precision 和F2-emeasure 在5/6个数据集是最优的,F-measure 在4/6个数据集优于所有对比算法,AUC 和recall 分别在3/6和2/6个数据集上取得所有对比算法的最优值.对比算法VMInaive在Colon 数据集的AUC、recall 和F-measure 优于对比算法,AUC 和recall 的值均为最大值1,但此时其F2-measure 为0,说明该算法将测试集的全部负类样本均误识为正类样本.算法CFR 在Colon 数据集也存在选择的特征子集的ELM 分类器的recall 指标为最大值1,但F2-measure 为0 的问题,也是将测试集的负类样本全部误识为正类样本造成的.另外,表7 的整体实验结果来看,GDFS+SFFS 算法选择的特征子集的分类性能是所有13个算法中最好的.

表7 各算法在表6 基因数据集的5-折交叉验证实验结果Table 7 The 5-fold cross-validation experimental results of all algorithms on datasets from Table 6

表7 各算法在表6 基因数据集的5-折交叉验证实验结果 (续表)Table 7 The 5-fold cross-validation experimental results of all algorithms on datasets from Table 6 (continued table)

以上分析显示:提出的特征子集评价准则GDFS 比原始DFS 准则更好,能选择出规模小且分类能力更好的特征子集;另外,GDFS 选择的特征子集的分类能力优于特征选择算法Relief、DRJMIM、mRMR、LLE Score、AVC、SVM-RFE、VMInaive、AMID、AMID-DWSFS、CFR 和FSSC-SD 所选特征子集的分类能力.

4.4 统计重要性检验

为了检验提出的GDFS+SFFS 特征选择算法与对比特征选择算法Relief、DRJMIM、mRMR、LLE Score、AVC、SVM-RFE、VMInaive、AMID、AMID-DWSFS、CFR、FSSC-SD以及DFS+SFFS 是否具有统计意义上的显著性区别,采用Friedman 检验来检验各算法之间的差异[49−51].在Friedman 检验检测到算法间的显著性不同之后,利用Nemenyi 后续检验来检测算法对的两算法之间是否存在统计意义上的显著性不同.根据Nemenyi 检验方法,在给定统计显著性水平α时,如果任一算法对的两算法之间的平均序数差小于临界阈值CD,则以置信度 1−α接受零假设 “两算法性能相同”,否则拒绝原(零)假设,认为两算法性能存在显著性不同.其中临界阈值CD=,这里的M和N 分别表示算法个数和数据集个数,qα可通过查表获取.各算法所选特征子集的ELM 分类器的Accuracy、AUC、recall、precision、F-measure 和F2-measure 在α=0.05 时的Friedman 检验结果如表8 所示.

由表8 的Friedma 检验结果可知,各算法所选特征子集的ELM 分类器的Accuracy、AUC、recall、precision、F-measure 和F2-measure 指标对应的p值均小于0.05.因此,我们可以拒绝零假设 “各特征选择算法性能相同”,则各算法所选特征子集在6个基因数据集上的分类性能存在显著性差异.

表8 各算法所选特征子集分类能力的Friedman 检测结果Table 8 The Friedman＇s test of the classification capability of feature subsets of all algorithms

在各算法存在显著性差异的基础上,采用Nemenyi 后续检验来进一步验证各算法对的两算法之间的性能是否显著性不同.当α=0.05,算法个√数为13 时,我们查表可知qα=3.13,由CD=计算可得临界阈值CD=7.4491,则可信水平为0.95 时,每一对算法采用其选择的特征子集对应ELM 分类器的Accuracy、AUC、recall、precision、F-measure 和F2-measure 指标值的Nemenyi 检验结果如图5 所示.

图5 各特征选择算法的Nemenyi 检验结果Fig.5 Nemenyi test results of 13 feature selection algorithms in terms of performance metrics of ELM built on their selected features

图5(a)的Nemenyi 检验结果显示,GDFS 在Accuracy 指标上与其他对比算法无显著差异.众所周知,基因数据集的不平衡性,分类准确率已经不适于评价特征子集分类性能[30].尽管如此,图5(a)的检验结果显示,GDFS 与其他12 种对比算法之间是存在差异的,与DFS 的差异最大,且优于DFS算法.图5(b)的Nemenyi 检验结果显示,GDFS在AUC 指标上与LLE Score 和CFR 算法存在显著性差异,且优于LLE Score 和CFR 算法,与其他10 种对比算法无显著差异,但存在差异,且GDFS 性能最优.图5(c)的Nemenyi 检验结果显示,GDFS 在recall 指标上与SVM-RFE 存在显著差异,与其他对比算法无显著差异,但从实验结果可以看出GDFS 与其他11 种特征选择算法间存在差异,且GDFS 性能最优,优于DFS 算法.图5(d)的Nemenyi 检验结果可见,GDFS 在precision 指标上与LLE Score、SVM-RFE 和CFR 算法存在显著性差异,且优于LLE Score、SVM-RFE 和CFR算法,与其他9 种对比算法无显著差异,但存在差异,且优于DFS,是13 种特征选择算法中性能最优的.图5(e)的Nemenyi 检验结果显示,GDFS 在Fmeasure 指标上与LLE Score 和SVM-RFE 算法存在显著性差异,且优于LLE Score 和SVM-RFE 算法,与其他10 种对比算法无显著差异,但存在差异,且GDFS 性能最优,优于DFS.图5(f)的Nemenyi 检验结果显示,GDFS 在F2-measure 指标上与LLE Score、CFR、VMInaive和AMID-DWSFS算法存在显著性差异,且优于LLE Score、VMInaive、AMID-DWSFS 和CFR 算法,与其他8 种对比算法无显著差异,但存在差异,且GDFS 性能最优,优于DFS.

图5 各算法的Nemenyi 检验结果还显示,对比算法DFS、Relief、DRJMIM、mRMR、LLE Score、AVC、SVM-RFE、VMInaive、AMID、AMIDDWSFS、CFR 和FSSC-SD,各对算法间不存在统计意义上的显著性差异.另外,提出的GDFS 优于DFS,尽管其间没有统计意义上的显著性差异,但图5 的Nemenyi 检验结果揭示,除了recall 指标,GDFS 与DFS 间的等级比较差异值大于2.5,且recall 指标时,GDFS 与DFS 的等级比较差异值也大于1.5,这说明尽管GDFS 与DFS 没有统计意义上的显著性差异,但其间存在差异.这一点与表7 的实验结果一致.

以上统计重要性分析显示:提出的GDFS 特征子集区分度评价准则优于原始DFS,GDFS+SFFS算法优于12个对比特征选择算法,能选择到分类性能更好的特征子集.12个对比算法两两之间不存在显著性差异.提出的GDFS 准则与原始DFS 特征子集评价准则选择的特征子集的分类能力有差异,且GDFS 优于DFS,但不存在统计意义上的显著性差异.

综合以上UCI 机器学习数据集和经典基因数据集的5-折交叉验证实验结果得出:提出的GDFS 特征子集区分度评价准则是一种有效的特征子集辨识能力评价准则,UCI 机器学习数据集和经典基因数据集的实验测试比较验证了基于该准则的特征选择算法能选择到分类性能更好的特征子集,达到了保持数据集辨识能力不变情况下进行数据维数压缩的目的.

5 结论

提出了一种特征子集区分能力评价新准则GDFS,克服了DFS 准则没有考虑特征测量量纲对特征子集区分能力大小影响的缺陷;GDFS 结合SFS、SBS、SFFS 和SBFS 搜索策略,以ELM 为分类器引导特征选择过程,提出GDFS+SFS、GDFS+SBS、GDFS+SFFS 和GDFS+SBFS 共4 种混合特征选择算法.

UCI 机器学习数据集和经典基因数据集的5-折交叉验证实验,以及与DFS 和经典特征选择算法Relief、DRJMIM、mRMR、LLE Score、AVC、SVM-RFE、VMInaive、AMID、AMID-DWSFS、CFR 和FSSC-SD 的性能比较和统计重要性检验表明,提出的GDFS 特征子集区分度评价准则是一种有效的特征子集辨识能力衡量准则,其选择的特征子集优于DFS、Relief、DRJMIM、mRMR、LLE Score、AVC、SVM-RFE、VMInaive、AMID、AMIDDWSFS、CFR 和FSSC-SD 选择的特征子集,具有更优的分类性能.GDFS 准则在提升和保持数据集辨识能力情况下降低了数据的维度.