基于事件触发的离散 MIMO 系统自适应评判容错控制

王 敏 黄龙旺 杨辰光

随着现代工业的快速发展,无线通信技术被广 泛用于各类控制系统中,以解决工业过程的远程控制问题,同时提高设备安装和配置的灵活性.例如,地面站对高空无人机的控制,以及控制台对作业车间中工业机器人的远程控制等都是借助无线通信技术来实现的[1−2].然而,在网络资源受限的情况下,传统的周期性数据传输和执行的控制方式很容易引发网络拥塞.针对该问题,文献[3]提出了事件触发的控制策略.该策略通过仅在满足触发机制要求时进行数据传输,从而有效地减少了控制系统中网络资源的占用.结合事件触发策略,自适应控制和万能逼近器等技术,大量针对不确定非线性系统的事件触发控制方案相继被提出[4−6].需要指出的是,上述方案极少考虑系统存在非匹配的不确定非线性动态情况,即不确定非线性动态出现在非控制输入通道.事实上,非匹配的非线性动态普遍存在于各种实际系统,如无人车,机械臂和飞行器等[7−12].针对嵌入了 “控制器−执行器网络”的非匹配非线性系统,国内外学者们提出了大量具有相对或绝对事件触发条件的控制方案[13−15].由于事件触发条件设计与系统稳定性的强耦合特性,导致上述方案很难拓展到嵌入 “传感器−控制器网络”的不确定非匹配非线性系统.为了解决该难题,文献[16]结合脉冲动力系统和死区算子等技术,提出了具有自适应事件触发条件的控制方案.需要说明的是,上述方案仅适合于连续系统.

相比于连续系统,离散系统更适用于描述数字化系统的控制过程.然而,离散系统事件触发控制方面的研究成果寥寥无几.造成这一现象的主要原因是直接利用反步法对离散非匹配系统进行控制器设计时,通常会产生非因果问题[17],故而难以将连续系统的研究成果直接推广到对应的离散系统上.为了克服该问题,文献[18]先将原系统转化成一个n步向前预测模型,并在该模型上进行反步控制设计.在假设网络资源充足的前提下,大量基于n步预测器的离散非匹配非线性系统的控制方案相继被提出[19−22].考虑到远程控制中网络资源受限问题,文献[23]尝试提出了基于n步预测模型的事件触发自适应神经网络控制方案.然而,文献[23]设计的控制器存在n步滞后现象,且触发条件复杂不便于实施.在此基础上,文献[24−25]探讨了随机噪声情况下离散非匹配非线性系统的事件触发控制问题.值得注意的是,上述的方案都没有考虑事件触发下系统的最优控制问题和可能出现的执行器故障现象.

众所周知,在资源受限的情况下考虑如何利用有限的资源来优化系统性能以及减少资源浪费是非常有必要的.动态规划是常用的解决最优化问题的有效方法之一,但是控制动态规划后向寻优的求解过程的矛盾以及系统维数较高时所导致的 “维数灾”问题,使得动态规划难以在系统的最优化控制中得到大规模的应用[26].为了解决此问题,文献[27]通过采用 “执行−评价”结构,提出了自适应评判设计方法.该方法使得执行网络能够根据评价结果适时调整控制策略,从而达到实时寻优的目的.目前,自适应评判设计被广泛应用于解决离散和连续系统的最优控制问题[21−22,28−30].如何将该方法推广到具有网络资源受限的离散非匹配非线性系统控制中是亟待解决的问题.此外,执行器故障广泛存在于工业生产过程中.执行器故障会导致系统性能下降,甚至导致系统不稳定[31−34].因此,在执行器故障下,研究离散非匹配非线性系统的事件触发自适应评判容错控制具有重要意义.

基于上述分析,本文着重研究具有非匹配结构的离散多输入多输出(Multi-input multi-output,MIMO)非线性系统的事件触发自适应评判容错控制问题.与现有的结果相比,本文的贡献可归纳如下:1)构造光滑的效用函数来构建系统的长期性能指标函数,从而避免了现有的非光滑二值效用函数切换过程中可能引起的评价网络和执行网络跳变现象;2)采用变量替换法将系统的将来信息表示成关于系统当前状态的函数,从而避免了控制设计过程中的非因果问题和控制信号的n步时延问题;3)通过在控制器中引入动态补偿项,并结合自适应评判设计方法,从而改善了系统控制性能和进一步降低了事件触发次数.

1 问题描述及预备知识

本文所考虑的网络控制系统模型如下

1.1 高阶神经网络

本文采用高阶神经网络(High-order neural network,HONN)来逼近未知的非线性动态,HONN 的结构能够用如下方程来描述:

1.2 事件触发机制

如图1 所示,本文主要考虑系统的传感器和控制器通讯时采用事件触发机制进行数据传输.当触发条件满足时,传感器将采集到的系统状态数据通过网络传输给控制器.为了便于事件触发条件的设计,本文定义如下的传输误差

图1 网络控制系统框图Fig.1 Schematic diagram of networked control systems

其中,kt表示上一个事件触发时刻,X(k) 为系统(1)的当前状态,X(kt) 为上一次传输的系统状态.

2 基于事件触发的自适应评判容错控制设计

在这一节中,针对所考虑的系统(1),本文提出了一种基于事件触发的自适应评判容错控制方案.

为了便于控制器设计,定义如下的误差变量

基于以上定义的误差变量(7)和中间函数(8),评价网络和执行网络的具体设计过程给出如下.

2.1 评价网络设计

首先,定义效用函数

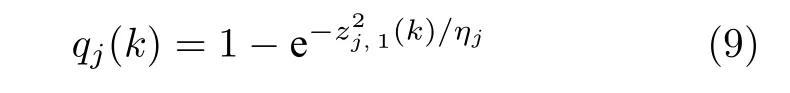
其中,ηj >0 是一个可调参数.根据式(9)可知,当跟踪误差zj,1(k)=0 时,qj(k)=0;当跟踪误差zj,1(k)→±∞时,qj(k)→1. 因此,qj(k) 可视作系统当前性能的评价.基于效用函数qj(k),定义系统长期性能指标函数

其中,0<ζj <1.根据定义(10)可得

式(11)也被称为Bellman 等式.采用评价网络对Qj(k) 进行逼近,则有

注 1.在评价网络的设计中,文献[22,31]都采用二值效用函数来构建长期的性能函数.由于评价网络与执行网络相关联,二值效用函数值的突变会对执行网络造成冲击,从而加速执行部件的老化和磨损.为了避免该问题,本文利用指数函数和跟踪误差zj,1(k) 定义了一个光滑的效用函数(9).从式(9)可知,qj(k) 的值在 [ 0,1) 之间连续变化,从而能够避免由于效用函数值的突变造成执行网络的冲击.

2.2 执行网络设计

这部分主要进行执行网络的设计.首先,利用反步法设计出理想的控制律,并用执行网络来对其进行逼近.具体设计过程如下.

根据式(19),式(21) 中的αj,1(k+1) 中包含系统的将来信息x1(k+1).若不加以处理,接下来设计出的虚拟控制律和实际控制律中都将包含系统的将来信息,导致所得出的控制律不可实现.为了解决该问题,本文利用变量替换的方法将αj,1(k+1)表示成关于系统当前状态的函数:

根据式(19)、(23)和中间函数(8),可推知

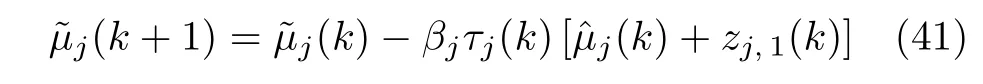
注 2.在控制器的设计中,不同于文献[18−22]所采用的n步向前预测模型方法,本文利用以当前时刻系统状态为变量的函数来刻画虚拟控制律的将来信息(26),从而成功避免了在离散系统控制设计过程中可能出现的非因果问题以及基于n步预测模型所导致的控制信号滞后n步的问题.

注 3.从式(26) 可知,虚拟控制律的将来信息(k+1)已经被表示为系统状态当前信息和参考信号将来信息的函数.类似于现有文献[18−22],本文假定参考信号是人为给定的,能够事先获得将来信息.此外,如果实际系统中参考信号的将来信息无法预先获得,那么可以构造ij步参考信号预测器,从而可以解决该问题.

注 4.注意到本文所考虑的系统(1) 是全状态可测的.然而,通过构造状态观测器[35]和引入控制增益函数(·)(j=1,2,···,N)是已知的约束,本文所提出的状态反馈控制方案很容易推广到系统状态不完全可测的情况.需要指出的是,在状态不完全可测的情况下,对于未知函数增益(·) 的处理目前仍是一个开放性和具有挑战性的问题.

3 主要结果

注意到事件触发机制设计的主要目的在于节省网络资源,该机制决定了是否将传感器采集到的当前时刻的系统数据发送给控制器.为了能够在节省网络带宽情况下仍然保证系统的控制性能,本文首先设计了如下的静态事件触发条件:

那么闭环系统中的所有信号都是最终一致有界的.

基于定理1 的研究结果,本文借鉴动态事件触发机制设计思想[36−37],进一步对定理1 的研究结果进行了推广.

定理 2.考虑离散多输入多输出系统(1),控制器(33)、(40),评价网络和执行网络的权值更新律(15) 和(37),以及设计如下的动态事件触发条件:

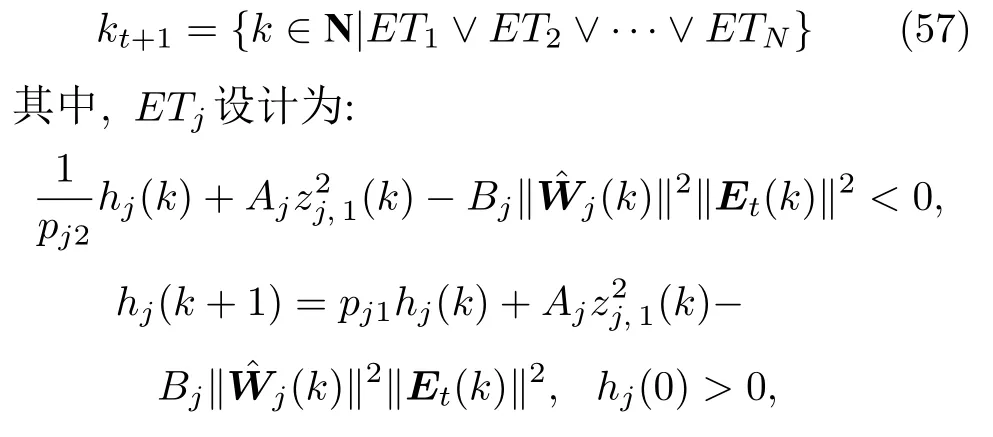
若设计参数laj,lcj,σaj,σcj,ϱj,rj,ij(ij=1,2,···,nj),0<ζj <1,0<βj <1,0<γaj <1/laj,0<γcj <1/lcj满足条件(43),且 01/pj1,那么闭环系统中的所有信号都是最终一致有界的.

定理2 的证明与定理1 类似,读者可自行证明.

注 5.定理2 通过在定理1 的静态事件触发条件(42)中引入额外的动态变量hj(k),构造出了典型的动态事件触发条件(57).随后,可以通过修改Lyapunov 函数为并采用类似定理1 的证明过程,很容易证明在动态事件触发条件(57)下闭环系统的所有信号也是最终一致有界的.此外,通过简单地分析可以得出,相比于静态事件触发条件(42),动态事件触发条件(57)能够进一步降低事件触发的次数.但需要指出的是,额外动态变量hj(k) 的引入,将导致动态事件触发条件(57) 的计算量有所增加.因此,在实际应用中,用户可以结合自身的网络带宽和处理器的情况选择适当的事件触发条件.

4 仿真验证

本章分别选取了数值算例和双连杆机械臂系统的仿真实例,来验证本文所提出的方案的有效性.

4.1 数值仿真

首先,考虑参考文献[19]中的数值模型:

仿真步长T=0.01 s,仿真步数N=2 000.仿真结果如图2～图7 所示.图2 和图3 表明了系统的输出能够很好地跟踪上给定的参考信号.图4 指示了事件触发间隔.从图5 可以看出,评价网络的输出始终在零附近,进一步说明系统取得了令人满意的控制性能.图6 和图7 表明了执行网络和评价网络的权值的有界性.在2 000 步仿真中,总的数据传输次数为843 次,较时间触发的控制方案减少了约60% 的网络资源占用.

图2 子系统1 输出跟踪效果Fig.2 Output tracking performance of subsystem 1

图3 子系统2 输出跟踪效果Fig.3 Output tracking performance of subsystem 2

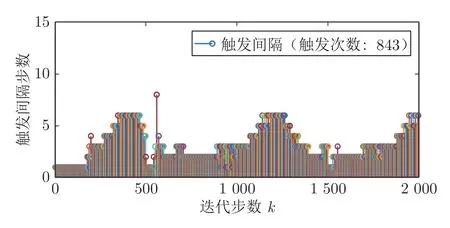
图4 事件触发间隔Fig.4 Event triggering interval

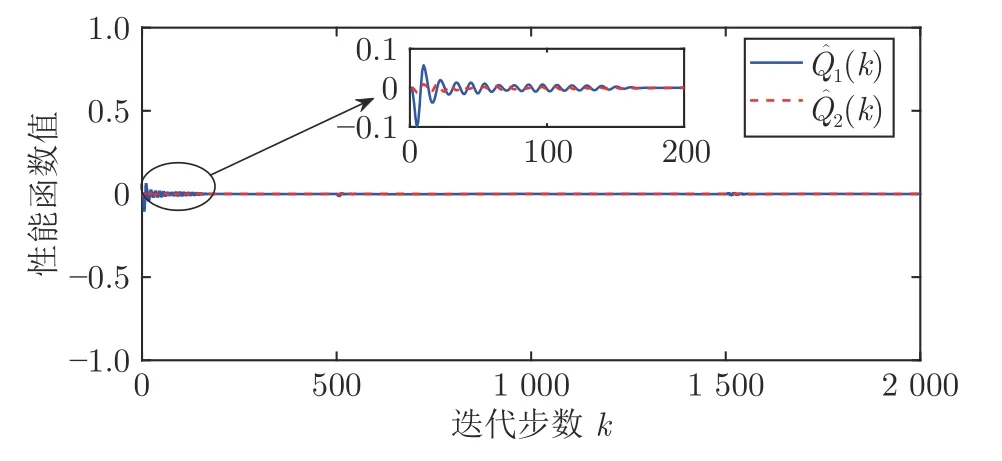
图5 长期性能函数Fig.5 Long-term performance function

图6 执行网络的权值范数Fig.6 Norm of action NN weights

图7 评价网络的权值范数Fig.7 Norm of critic NN weights

此外,本文进行了两组对比仿真实验,并采用平均绝对误差(Mean absolute error,MAE) 和平均带宽占用(Average bandwidth occupation,ABO)来对系统的性能进行定量刻画:

其中,ne表示总的数据传输次数,pL表示一次发送的数据包长度,bL表示数据类型的比特长度,T ×N表示时间长度.在仿真中,传输的向量X(k) 中包含4个元素,数据类型为float.由此可计算pL=4,bL=32bit.

第1 组对比实验的结果见表1.通过对比表格1 中的数据,可以看出执行器故障补偿机制和光滑的效用函数在改善系统性能方面的有效性.第2 组对比实验的结果见表2.为了便于表示,表2 中“SETC” (Static event-triggered condition)代表静态事件触发条件;“DETC” (Dynamical eventtriggered condition) 代表动态事件触发条件,“CPU”(Central processing unit)代表电脑中央处理器.对比表2 中的数据可知,DETC (57) (pj1=0.01,pj2=101) 相比于SETC (42)而言,能够进一步减少事件触发次数,同时也因为动态变量hj(k) 的引入导致了算法计算量的增加.

表1 仿真实验对比1Table 1 Comparison of simulation results

表2 仿真实验对比2Table 2 Comparison of simulation results

4.2 实例仿真

为了进一步说明本文方案的有效性,本文对双连杆机械臂模型进行了仿真实验.已知双连杆机械臂的欧拉−拉格朗日动力学模型[29]为:

图8 例2 关节1 的输出跟踪效果Fig.8 Tracking performance of joint 1 of Example 2

5 总结与展望

图9 例2 关节2 的输出跟踪效果Fig.9 Tracking performance of joint 2 of Example 2

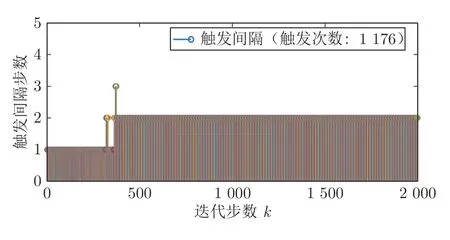
图10 例2 的事件触发间隔Fig.10 Event triggering interval of Example 2

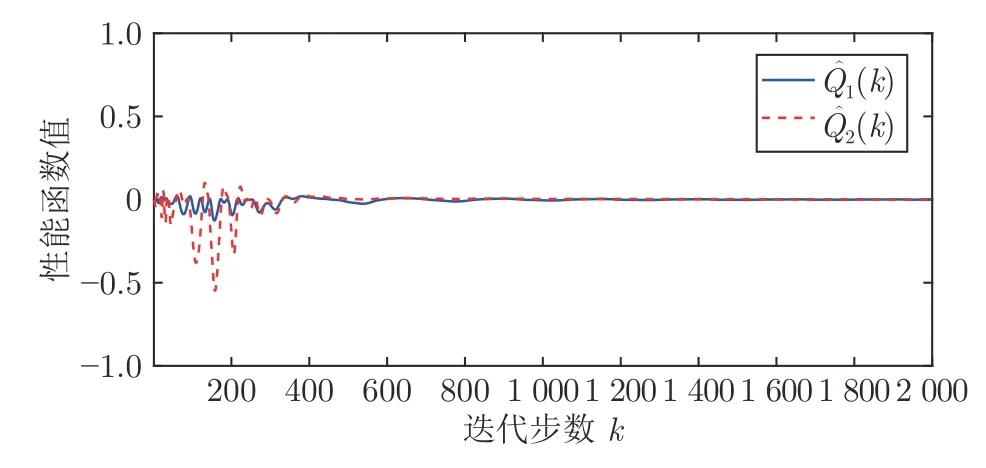
图11 例2 的长期性能指标函数Fig.11 Long-term performance function of Example 2

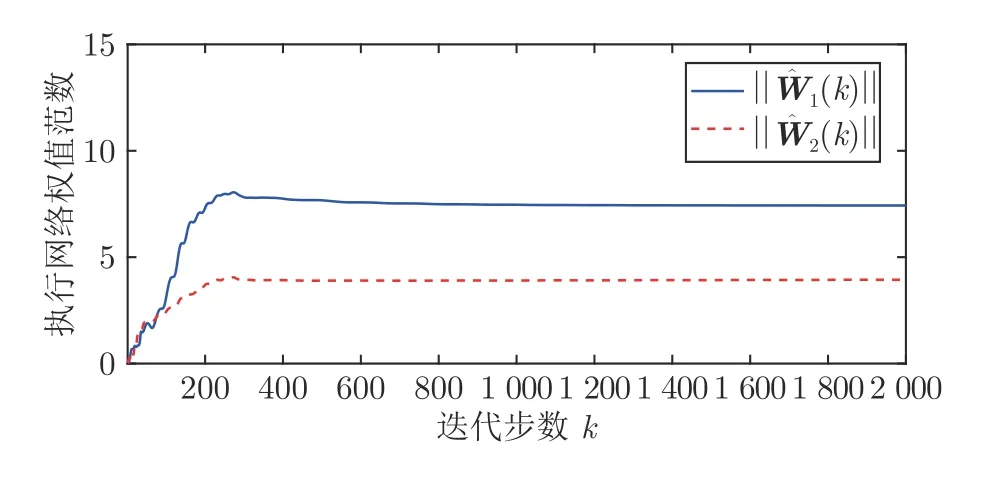
图12 例2 的执行网络权值范数Fig.12 Norm of action NN weights of Example 2

图13 例2 的评价网络权值范数Fig.13 Norm of critic NN weights of Example 2

本文针对存在执行器故障的离散MIMO 严格反馈非线性系统的最优跟踪控制问题,提出了一种基于事件触发的自适应评判控制设计方案.相比于现有的基于n步预测模型的控制方案,本文所提出的基于变量替换控制方案避免了控制信号的n步时延问题.此外,通过设计执行器故障补偿机制,事件触发机制与自适应评判机制,本文所提出的控制方案不仅节省了网络资源占用,而且改善了系统的控制性能.最后仿真结果验证了本文所提出的方案的有效性.注意到在离散系统的网络控制方面仍然有诸多待解决的问题,例如数据丢包[38],网络攻击[39],执行器故障估计[40−41]等,这些问题将是我们未来的工作方向.