基于自适应LASSO 先验的稀疏贝叶斯学习算法
白宗龙 师黎明 孙金玮
稀疏信号恢复具有广泛的应用性和充分的理论支持,因此成为信号处理领域中的一个重要且受到持续关注的研究课题.稀疏信号恢复可应用于麦克风阵列信号处理[1−3],图像处理[4−9],脑电信号处理[10−11],雷达信号处理[12−14]等领域.目前,有多种稀疏信号恢复算法被提出,主要包括基于ℓp范数(0
SBL 与其他贝叶斯算法类似,通过赋予信号稀疏先验分布,最大化后验分布得到信号的估计.与其他贝叶斯方法不同的是SBL 采取构建多层贝叶斯框架的方式赋予信号中每个元素独立的稀疏分布,根据稀疏分布的不同,SBL 可以分为基于Student-t 先验的SBL[16],基于Laplace 先验的SBL[17−18],基于合成LASSO 先验的分布等[19].SBL 最早在文献[16]中提出,该文献中构建了一种多层贝叶斯框架,通过赋予信号中每个元素多层共轭先验,等价赋予信号Student-t 稀疏先验.多层共轭先验的贝叶斯框架的构造使得模型中每层参数可以依次更新.类似的,文献[17]提出一种基于Laplace 先验的多层贝叶斯框架.文献[18]中提出一种针对复值信号的自聚焦的基于Laplace 先验的多层贝叶斯框架.文献[19]中提出一种基于合成LASSO 先验的多层贝叶斯框架,赋予信号LASSO 先验.由于LASSO 分布缺少共轭先验,文中采用了高斯接近的方法进行求解.该文献对应于在文献[20]中提出的一种基于凸优化的自适应LASSO 算法.
由于SBL 算法在参数更新时需要矩阵求逆运算,导致计算量很高.为降低计算复杂度,文献[21]提出一种基于基选择的快速SBL 算法,文献[17]给出了Lalapce 先验下基于基选择的快速算法,但是该算法无法推广至复值信号模型.文献[22]提出一种基于最大化证据下界的快速算法,但是该算法稳定性欠佳,存在不收敛的情况.文献[23]提出一种基于近似消息传递(Approximate message passing,AMP)的SBL 算法,并在文献[24]针对相干信号进行进一步改进.文献[25]提出一种基于空间轮换的SBL 算法.文献[26]在[25]基础上提出一种应用于大数据量的基于标量平均场的SBL 算法.
为提高稀疏信号恢复的准确性,本文开展了基于自适应LASSO 先验的SBL 算法研究.在贝叶斯模型构造阶段,本文中通过构建一种与现有SBL 算法不同的多层贝叶斯框架,赋予信号中每个元素具有独立权重的LASSO 先验,比现有稀疏先验更有效的鼓励稀疏.根据该多层贝叶斯框架提出一种基于自适应LASSO 先验的SBL 算法.为进一步降低提出算法的计算复杂度,在贝叶斯推断阶段利用空间轮换技术避免矩阵求逆运算,形成一种快速算法.

1 稀疏信号恢复问题描述
稀疏信号恢复问题是指已知测量矩阵A ∈RM×N,利用欠采样数据x ∈RM和稀疏恢复算法估计稀疏信号g ∈RN的问题.实值稀疏信号恢复的数学模型表示如下:

其中,w ∈RM是可加性高斯白噪声.复值信号模型与实值信号模型的区别在于测量矩阵A ∈CM×N是复值矩阵,测量数据x ∈CM和稀疏信号g ∈CN是复值向量,w ∈CM是复值圆周对称高斯白噪声.
由于测量数据x是欠采样数据,即数据维度M小于信号维度N,因此使用最小二乘算法求解信号g是一个不适定问题.然而,Candes 等在文献[27]中证明了在已知信号g是稀疏信号且满足有限等距性质(Restricted isometry property,RIP)条件下,稀疏信号恢复问题具有唯一解.为了利用信号的稀疏先验信息,最直接的方法是添加正则项∥g∥0约束解的范围.从而将稀疏信号恢复问题转化为如下优化问题:

其中,ζ是正则化因子.然而,凸优化问题 (2)是一个NP-hard 问题,难以进行求解.常用的求解问题(2)的方法是将ℓ0范数释放至ℓ1范数,形成如下凸优化问题:

其中,∥·∥1表示ℓ1范数.凸优化问题 (3)可以通过LASSO 算法进行求解,但是LASSO 算法不能一定保证收敛,为提高算法性能,Zou 在文献[20]中对LASSO 算法进行了改进,提出了自适应LASSO算法,并对该算法的Oracle 特性进行了证明1Oracle 特性具体包括模型选择相和性和参数估计渐进正态性.其含义为,在一些变量不是提前已知的情况下,如果算法具有Oracle 特性,那么它能够筛选出正确的预测的概率为1 而且能够有效而正确地估计非零估计量..自适应LASSO 算法求解如下优化问题:

其中,gi是信号g中的第i个元素,ωi表示信号元素gi的权重.
本文利用稀疏贝叶斯框架构建了基于自适应LASSO 先验的SBL 算法,通过构建多层贝叶斯网络赋予信号中每个元素独立信号的LASSO 先验,从而实现贝叶斯框架下的自适应LASSO 算法.
2 贝叶斯模型
在贝叶斯模型中,所有未知变量都被认为是随机变量,并根据未知变量的先验信息赋予随机变量不同的分布.本文中根据信号的稀疏特性赋予未知信号g自适应LASSO 先验分布p(g|η),并且假设测量数据x是一个条件概率为p(x|g,ρ) 的随机过程.其中,ρ表示噪声的精度,即噪声方差的倒数.下面将对该多层贝叶斯框架进行具体的描述.
2.1 观测模型
假定实值模型中观测噪声w是方差为ρ−1的高斯白噪声,复值模型中观测噪声w是方差为ρ−1的圆周共轭复高斯白噪声,则实值模型和复值模型中测量数据x的条件概率表示如下:

其中,ς=2 对应于实值模型,ς=1 对应于复值模型.为更新噪声精度ρ,假设ρ服从于如下Gamma分布:

其中,c和d是预设的模型参数,且c>0 是Gamma分布的形状参数,d>0 是Gamma 分布的尺度参数.在变量ρ服从于Gamma 分布 (6)的假定下,变量的均值和方差分别表示为.
2.2 信号模型
类似于其它SBL 算法,未知信号g的自适应LASSO 先验p(g|η) 通过多层共轭先验的形式实现.首先,使用零均值的多维高斯分布对信号进行如下建模:

其中,Λ=diag{λ}表示多维高斯分布的协方差矩阵,λ=[λ1,λ2,···,λN]T表示信号的方差向量且λi >0,d iag{·}表示对角矩阵操作.对于变量λ,假设其服从于如下独立的Gamma 分布:

其中,η=[η1,η2,···,ηN]T表示变量的向量且ηi >0.根据式 (7)和 (8),变量g关于变量η的边缘分布可以通过对变量λ积分获得,表示如下:

即,前两层贝叶斯先验 (7)和 (8)等价与赋予信号g一种LASSO 先验,其中,ηi对应于式 (4)中的权重wi.为了自适应调节LASSO 先验的权重,对非负变量η赋予如下Gamma 分布:

其中,ai >0 和bi >0 为预设的模型参数.
根据式 (9)和 (10),变量g关于a和b的边缘分布可通过对变量η的积分获得,结果如下:

其 中,Γ(·) 表示Gamma 函数.实际 上,根据式(11),本文提出的贝叶斯框架最终赋予信号g一种Student-t 先验.其中,Student-t 分布是一种具有长拖尾特性的分布,可以表达信号的稀疏特性[16].基于自适应LASSO 先验的SBL 模型由式 (5),(7),(8),(10)构成.该模型的因子图如图1 所示.图中节点函数总结如下:


图1 基于自适应LASSO 先验的SBL 框架的因子图Fig.1 The factor graph of the proposed SBL framework using adaptive LASSO priors
2.3 基于自适应LASSO 先验SBL 算法的稀疏恢复原理分析
SBL 算法本质是一种鲁棒的最大后验估计方法[2,16].一般通过I 型或II 型估计器稀疏求解[28].本文采用I 型估计器对提出的基于自适应LASSO先验SBL 算法进行分析.I 型估计器为最大化后验分布[28]:

在SBL 算法中,通过迭代的方式对参数进行更新,对于每一次迭代需要使用上一次迭代的参数.即在每一步迭代中等价于如下优化问题:

其中,gnew和gold分别是本次迭代和上一次迭代中g的估计.根据式 (9),式 (14) 可写为如下形式:

由Laplace 分布和Gamma 分布的共轭性质可得,变量η服从于如下Gamma 分布:

比较式 (17)和式 (4)可知,本文提出的基于自适应LASSO 先验的SBL 算法对应于自适应LASSO 算法.自适应LASSO 算法需要预定义回归系数,但本文中算法具有自回归特性,可自适应选择合适的回归系数,并且SBL 算法具有不确定估计特性,估计结果在统计意义上优于自适应LASSO算法.根据文献[20],自适应LASSO 算法是对LASSO 算法的改进,稀疏恢复性能优于LASSO 算法.又根据文献[17],基于Laplace 先验的SBL 算法对应于LASSO 算法,并且性能优于基于Student-t算法.文献[19]提出的基于合成LASSO 先验的SBL算法对应于自适应LASSO 算法,但是由于采用高斯接近的方法进行参数更新,导致在测量数少或者SNR 低时存在无法进行高斯拟合的情况.本文提出的基于自适应LASSO 先验的SBL 算法通过多层贝叶斯框架的方式构造自适应LASSO 先验,避免了无法拟合的情况.通过以上分析可知,本文提出的基于基于自适应LASSO 先验的SBL 算法性能优于现有算法.
为更直观的表现本文提出的算法所提供的稀疏恢复特性,我们绘制了实值模型下不同算法的稀疏先验的代价函数的二位等高线图,结果见图2.复值信号模型与实值信号模型的结果类似,此处不再重复讨论.图中BPDN 是文献[29]提出的算法,FastSBL是文献[21]提出的基于Student-t 先验的SBL 算法,FastLap-SBL 是文献[17]提出基于Laplace 先验的SBL 算法,aLASSO-SBL 是本文提出的基于自适应LASSO 先验的SBL 算法.其中,BPDN 和FastLap-SBL 的先验与参数无关;FastSBL 和aLASSO-SBL 算法的参数设置相同,都为a=1,b=0.1.根据文献[16]、文献[30]和文献[19],如果先验具有长拖尾特性并且概率分布在零点处越 “尖锐”则越鼓励稀疏,反映到二维等高线图上为越靠近坐标轴,越鼓励稀疏.观察图2,自适应LASSO先验的二维等高线图相比于其他先验更靠近坐标轴.由图中可知,本文提出的算法比其他算法有更好的稀疏恢复性.
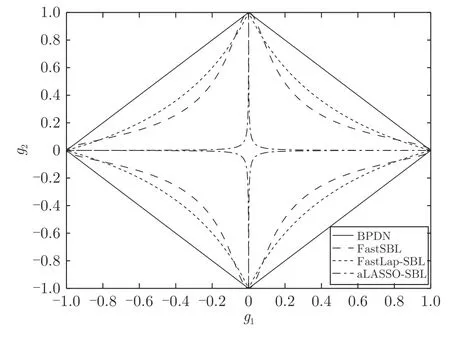
图2 四种算法的稀疏先验代价函数二维等高线图Fig.2 Two dimensional contour plots of cost functions of different sparse priors
另外,我们绘制了不同参数下自适应LASSO先验的代价函数等高线图,如图3 所示,在参数a固定为 1 的条件下,参数b越接近于 0,二维等高线越靠近坐标轴,即算法提供的解越稀疏.基于以上分析,相比于其它算法,本文提出的算法在理论上可以提供最稀疏的解,从而得到更精确的稀疏信号恢复性能.

图3 本算法在不同参数下稀疏先验代价函数二维等高线图Fig.3 Two dimensional contour plots of cost functions of the proposed sparse priors versus hyperparameters
3 变元贝叶斯推断
在本文提出的贝叶斯模型中,所有隐藏变量的集合表示为 Θ ={g,λ,η,ρ}.根据图1 表示的贝叶斯模型,联合概率密度表示如下:
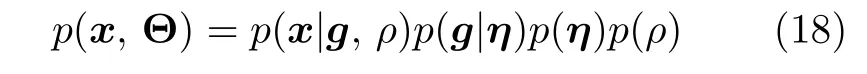
后验分布的闭合形式p(Θ|x) 需要计算边缘分布密度函数p(x),但是p(x) 难以求得,因此本文采用变元贝叶斯推断的方法进行参数更新.变元贝叶斯推断使用因子化变量分布对实际后验分布进行近似.隐藏变量的因子化变量分布表示如下:

其中,q(Θ) 是实际后验p(Θ|x) 的近似.然后,通过最小化实际后验分布p(Θ|x) 与近似分布q(Θ) 的KL 散度(Kullback-Leibler,KL)对参数进行更新,该过程等价于最大化如下目标函数:

如图1 所示,本文提出的模型中所有节点的先验和似然函数都存在共轭指数分布族,因此变元贝叶斯推断表示如下[31−32]:

其中,θk表示隐藏变量集合 Θ 中第k个变量,例如θ1表示变量g,Θθk表示集合 Θ 中去除第k个变量θk的集合,C表示常数.
3.1 参数更新
根据式 (18),对数形式的联合分布表示如下:
然后,参数可根据式 (21)和 (22)更新,下面给出具体更新规则.
参数g的更新:根据式 (21),实际后验分布p(g|x)的变元近似分布的对数形式为
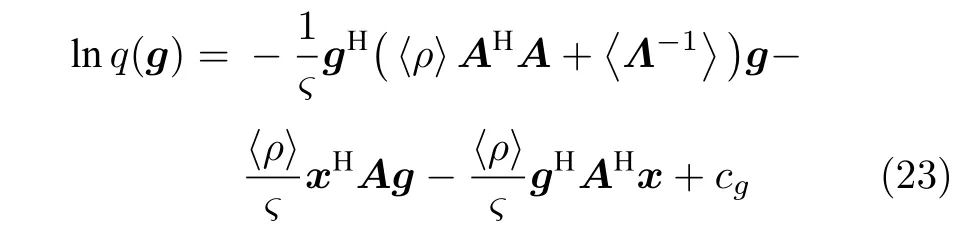
其中,〈·〉表示参数的期望,cg表示更新参数g时的常量.由式 (23)可知,q(g) 可以使用多维高斯分布表示,其期望和方差表示如下:

其中,IM表示维度为M的单位矩阵.式 (24b)的推导使用了Woodbury 引理[33],目的是降低矩阵求逆的计算量.其中,Woodbury 引理见附录A.
参数λ的更新:变量λ的对数近似后验为:

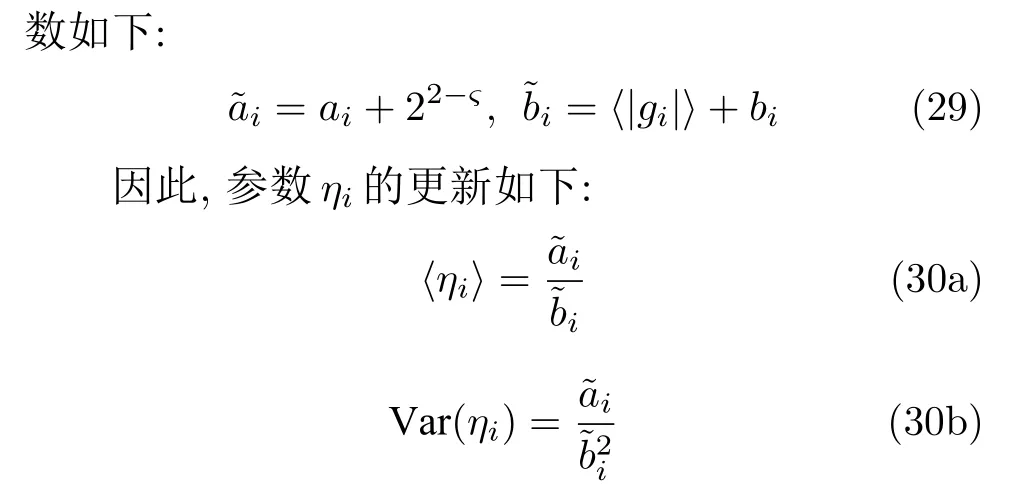
参数ρ的更新:根据式 (21)和式 (22),变量ρ的对数近似分布表示如下:
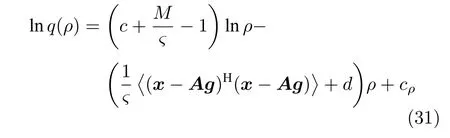
其中,cρ表示参数ρ更新时的常量.根据式 (31),变量ρ的近似分布为Gamma 分布,对应参数如下:

其中,t r(·) 表示矩阵的迹.因此,参数ρ的更新规则为:

上述为本文提出的基于自适应LASSO 先验的SBL 算法所有参数的更新规则,以下将该算法简称为aLASSO-SBL.为清晰描述算法,将参数更新流程总结如算法1 所示.
算法1.aLASSO-SBL 算法伪代码


3.2 快速算法
根据参数更新规则,算法的主要计算量在于更新参数g的协方差矩阵 Σ.为进一步降低算法计算量,本文采用空间轮换方法对参数g进行更新.在g中元素相互独立的假设下,根据式 (21),变量gi的对数近似分布表示如下:

快速算法的参数更新流程与第3.1 节中aLASSO-SBL 算法的区别在于参数g的更新,即使用式(36)替代式(24)进行更新,其余参数更新规则不变.快速算法的优势在于更新参数g的协方差矩阵 Σ 时避免了矩阵求逆运算,从而降低计算量,缺点在于忽略了变量g不同元素之间的协方差项,所以在测量矩阵A的列向量相关的情况下,快速算法的稀疏信号恢复准确度会降低.为描述方便,下文中将快速算法简称为FaLASSO-SBL 算法.
算法2.FaLASSO-SBL 算法伪代码

3.3 算法计算量分析
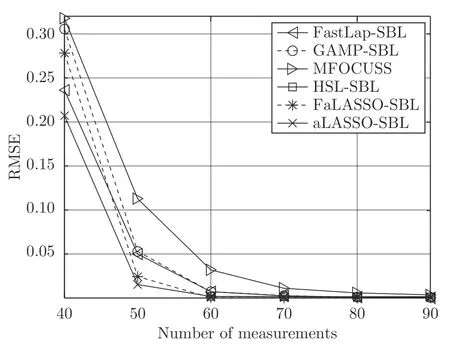
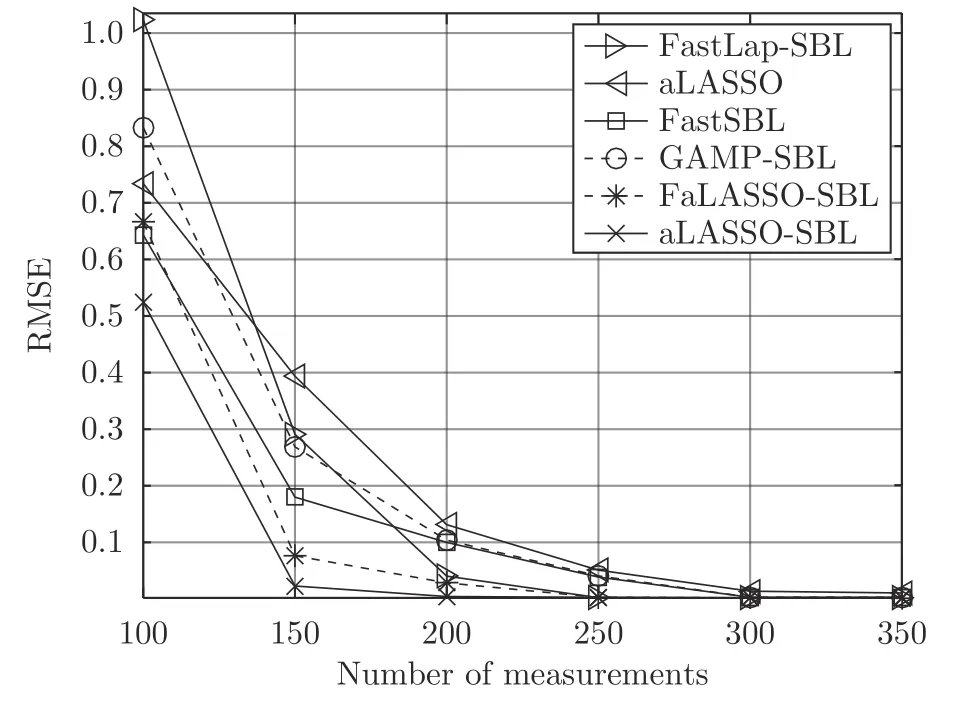
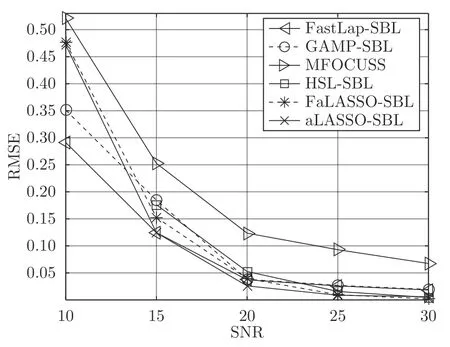
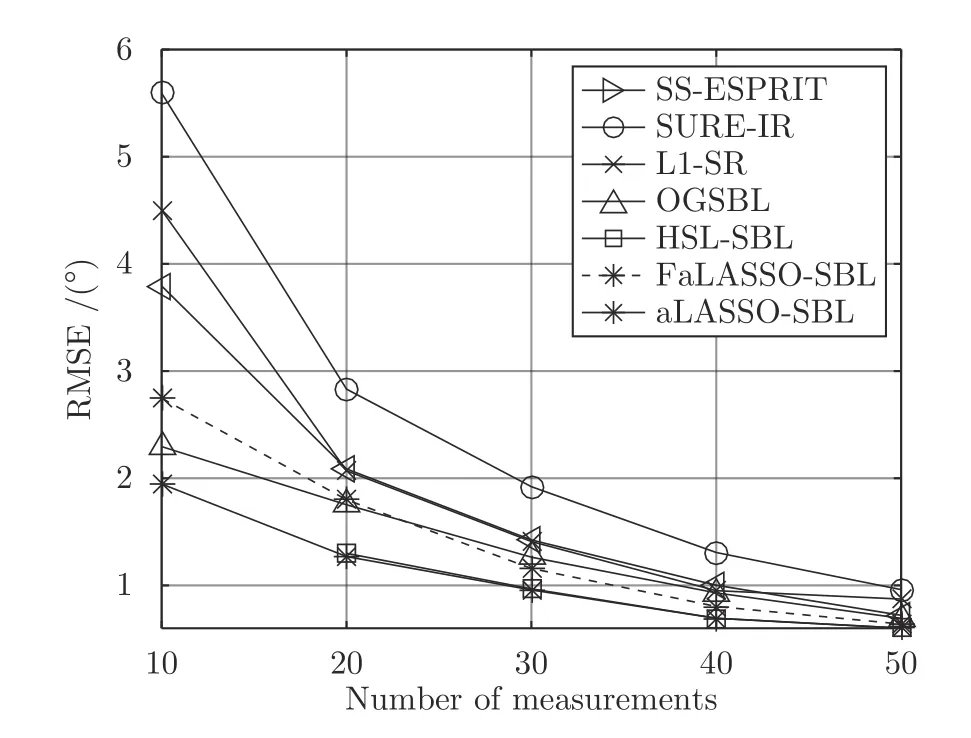
本文通过使用算法中的乘法或除法运算数量衡量计算复杂度,并且在欠定条件 (M 本节通过仿真实验验证提出的aLASSO-SBL和FaLASSO-SBL 算法的性能.仿真实验分别针对实值信号模型(ς=2 )和复值信号模型(ς=1)开展.对于实值信号模型,测量矩阵A中的元素满足独立同分布的高斯分布,稀疏信号g中非零元素服从于独立同分布的高斯分布.对于复值信号模型,测量矩阵A中的元素和稀疏信号g中的非零元素都服从于独立同分布的复高斯分布.无噪测量数据通过测量矩阵A与和稀疏信号g相乘得到,即Ag,然后对信号添加高斯白噪声,信噪比(Signal-Noise Ratio,SNR)的定义如下: 各个算法的稀疏恢复准确性通过均方根误差(Root-Mean-Square-Error,RMSE)衡量,定义如下: 本文使用的算法及相应简称总结如下:BPDN 为文献[29]提出的基追踪去噪算法,OMP 为文献[34] 提出的正交基追踪算法,aLASSO 为文献[20]提出的自适应LASSO 算法,FastSBL 为文献[21] 提出的快速SBL 算法,GAMP-SBL 为文献[24]中提出的基于近似消息传递(Approximate Message Passing,AMP)的SBL 算法,FastLap-SBL 为文献[17]提出的基于Laplace 先验的快速SBL 算法,MFOCUSS 为文献[35]提出的类ℓp范数优化算法,HSL-SBL 为文献[19] 提出的合成LASSO 先验的SBL 算法,aLASSO-SBL 和FaLASSO-SBL 是本文提出的基于自适应LASSO 先验的SBL 算法及其快速算法.其中,aLASSO 的正则因子设置为 1,MFOCUSS 的参数p按文中建议设为 0.8,FastSBL,Lap-SBL,HSL-SBL,aLASSOSBL 和FaLASSO-SBL 的模型参数设置为相同的接近于零的值 10−6. 本文中所有仿真实验使用MATLAB 软件实现,软件版本为R2020a,操作系统为64 位Windows 10.硬件配置总结如下:处理器为AMD Ryzen 7 4750U,物理核心数为8,主频为1.7 GHz,内存容量为16 GB. 与凸优化和贪婪算法相比,贝叶斯方法的一个重要特性是可以提供未知信号的后验分布而非点估计结果.利用后验分布估计参数的优势在于通过协方差矩阵 Σ 可以得到参数估计的不确定度,在统计的角度优于凸优化算法.本次实验中我们给出实值模型下各个算法对稀疏信号的估计结果.仿真中测量矩阵的维度为 5 0×200,即测量数为 50,信号长度为 2 00,信号中非零元素的个数设置为 10,SNR设置为30 dB.实验结果如图4 所示.其中,图4(a)为纯净的稀疏信号;图4(b)为使用BPDN 算法恢复的信号;图4(c)为使用aLASSO 算法恢复的信号;图4(d)为使用OMP 算法恢复的信号;图4(e)为使用FaLASSO-SBL 算法恢复的信号;图4(f)为使用aLASSO-SBL 算法恢复的信号.由图4 可知.基于凸优化的BPDN 和aLASSO 算法以及基于贪婪算法的OMP 算法仅提供点估计结果,而本文提出的aLASSO-SBL 和FaLASSO-SBL 算法与其它贝叶斯算法相同,可以提供具有不确定度的估计结果.其中,图中误差线表示恢复信号的不确定度.由于FaLASSO-SBL 算法忽略协方差项导致对信号方差的估计小于aLASSO-SBL 算法估计的方差,但是协方差项的忽略会导致稀疏信号恢复准确性降低(见仿真实验二,三和四). 图4 一维信号稀疏恢复图Fig.4 Results for one-dimensional signal recovery 本次仿真实验研究各个算法稀疏恢复性能与测量数的关系.对于实值信号模型,信号长度设置为200 ,非零元素数设置为 30 ,测量数变化范围为50到 100,间隔为 10.SNR 为30 dB.独立实验次数为200 次.对于复值信号模型,测量数变化范围为40到 90,其它参数设置与实值信号模型相同,原因是相同维度下,复值测量数据的信息量大于实值测量数据的信息量,所以需要更少的测量数.实值信号模型和复值信号模型的实验结果如图5 和图6 所示.表1 给出了测量数为 80 时实值信号模型和复值信号模型下各算法单次运行的时间. 图5 实值模型下各算法稀疏恢复准确度与测量数的关系Fig.5 RMSE of different algorithms with the real-value signal model versus length of measurements 图6 复值模型下各算法稀疏恢复准确度与测量数的关系Fig.6 RMSE of different algorithms with the complexvalue signal model versus length of measurements 由图5 可知,针对实值信号模型,当测量数M=50 时,所有算法失效.当测量数M ≥60 时,本文提出的aLASSO-SBL 的稀疏恢复准确性优于其他算法,特别是在测量数较小(6 0≤M ≤90)时恢复效果相较于其它算法有明显提升.快速算法FaLASSOSBL 算法的准确性相比于aLASSO-SBL 算法有一定程度的降低,但是如表1 所示,FaLASSO-SBL算法计算时间明显低于aLASSO-SBL 算法.根据图5 和表1,FastLap-SBL 算法和GAMP-SBL 算法的运算速度比本文提出的FaLASSO-SBL 算法快,但是信号恢复的准确度比本文提出的算法低. 如图6 所示,对于复值信号模型,所有算法在测量数 7 0≤M ≤90 时稀疏恢复效果较好,在测量数 5 0≤M ≤70 时,本文提出的aLASSO-SBL 和FaLASSO-SBL 算法相比于其他算法具有更低的RMSE.在测量数M=40 时,所有算法的恢复效果很差.在测量数M ≥60 时,HSL-SBL 算法与本文提出的算法有相同的稀疏恢复效果,但是HSLSBL 算法在测量数小于 60 时出现不收敛的情况,所以无法显示其在M <60 时的结果.相比HSLSBL 算法,本文提出的算法稳定性较高.根据图6和表1,对于复值信号模型,MFOCUSS 算法和GAMP-SBL 算法的计算速度比本文提出的FaLASSO-SBL 算法速度快,但信号恢复的准确率低于本文提出的算法.原因是MFOCUSS 算法在归一化因子选择不合适时准确性降低;GAMP-SBL 是一种基于Student-t 先验的快速SBL 算法,其优势在于计算速度快,但缺点在于其信号恢复的准确率低于基于Student-t 先验的SBL 算法. 为进一步验证本文中提出的aLASSO-SBL 算法对高维信号的稀疏恢复性能,进行如下仿真实验.对于实值信号模型,信号长度设置为 2 000,非零元素数设置为 100,测量数变化范围为 100 到 3 50,间隔为 50. SNR 为20 dB.独立实验次数为 2 00 次.复值信号模型参数设置与实值信号模型相同.仿真实验结果如图7 和图8 所示. 图7 高维实值信号模型下各算法稀疏恢复准确度与测量数的关系Fig.7 RMSE of different algorithms with the high-dimensional real-value signal model versus length of measurements 图8 高维复值信号模型下各算法稀疏恢复准确度与测量数的关系Fig.8 RMSE of different algorithms with the high-dimensional complex-value signal model versus length of measurements 图7 为高维信号实值模型下各算法稀疏恢复准确度与测量数的关系.由图7 可知,本文提出的aLASSO-SBL 算法的稀疏信号恢复准确性优于现有稀疏恢复算法.本文FaLASSO-SBL 算法的准确性比aLASSO-SBL 算法有所降低,但在测量数M ≥150时高于其他算法.图8 为高维信号复值模型下各算法稀疏恢复准确度与测量数的关系.由图8 可知,HSL-SBL 算法在M ≥150 时与本文提出的aLASSO-SBL 算法的稀疏信号恢复准确度相同并且高于其它算法,但是当M <150 时失效.本文FaLASSO-SBL 算法的准确性比aLASSO-SBL算法略低,但在M ≥150 时高于除aLASSO-SBL算法和HSL-SBL 算法之外的其它算法,但计算量低于aLASSO-SBL 算法和HSL-SBL 算法. 表2 给出了高维信号实值模型和复值模型在测量长度为200 时单次运行需要的时间.与表1 相比可知,信号维度增加会导致计算量的增加.结合表2、图7 和图8 可知,对于高维信号,本文中提出的aLASSO-SBL 算法的稀疏信号恢复准确性高于现有算法,但是在信号维度增高时计算量会显著增加;本文中提出的FaLASSO-SBL 算法稀疏恢复准确性略低于aLASSO-SBL 算法,但运算速度明显高于aLASSO-SBL 算法. 表2 恢复高维信号时各算法单次运行时间Table 2 Time consumptions of different algorithms when the dimension of signal is high 本次仿真实验研究各个算法稀疏恢复性能和稀疏度的关系.对于实值信号模型,测量矩阵的维度设置为 100×200,即测量数为 100,信号长度为200信号中非零元素个数变化范围为 10 到 50,间隔为10. SNR 设置为30 dB.独立实验次数为 2 00.对于复值信号模型,信号中非零元度的个数变化范围设置为 20 到 70,其他参数设置与实值模型设置相同.针对实值信号模型和复值信号模型的稀疏恢复结果如图9 和图10 所示. 根据图9 可知,针对实值信号模型,所有算法在稀疏度高的条件下,即信号中非零元素个数10≤K ≤30时稀疏恢复效果较好,在稀疏度低的条件下(3 0≤K ≤60),FaLASSO-SBL 和aLASSOSBL 的RMSE 明显低于其它算法,即本文提出的算法对信号稀疏度的鲁棒性比其它常用算法更强. 图9 实值模型下各算法稀疏恢复准确度与稀疏度的关系Fig.9 RMSE of different algorithms with the real-value signal model versus number of non-zero elements 如图10 所示,针对复值信号模型,MFOCUSS算法的恢复效果比贝叶斯算法的恢复效果差.比较贝叶斯算法,HSL-SBL 与aLASSO-SBL 算法的恢复效果处于相同水平,优于其它算法,FaLASSOSBL 算法作为aLASSO-SBL 的快速算法,在信号非零元素个数增加到一定程度 (K ≥60) 时稀疏信号恢复的准确性有所下降. 图10 复值模型下各算法稀疏恢复准确度与稀疏度的关系Fig.10 RMSE of different algorithms with the complexvalue signal model versus number of non-zero elements 与仿真二相同,为了进一步验证本文提出的算法对高维稀疏信号的恢复性能,进行如下仿真实验.对于实值信号模型,信号长度设置为 2 000,测量数设置为 2 00,信号中非零元素数目变化范围为 20 到120 ,间隔为 20.SNR 为20 dB.独立实验次数为200次.对于复值信号模型,信号中非零元素数目变化范围为 2 0 到1 60 ,间隔为 20,其它参数设置与实值信号模型相同.仿真实验结果如图11 和图12所示. 图11 高维实值信号模型下各算法稀疏恢复准确度与稀疏度的关系Fig.11 RMSE of different algorithms with the high-dimensional real-value signal model versus number of non-zero elements 图12 高维复值信号模型下各算法稀疏恢复准确度与稀疏度的关系Fig.12 RMSE of different algorithms with the high-dimensional complex-value signal model versus number of non-zero elements 图11 为高维信号实值模型下的稀疏恢复准确度与稀疏度之间的关系.如图所示,本文提出的aLASSO-SBL 算法的稀疏恢复准确度高于现有算法,本文提出的FaLASSO-SBL 算法准确度在非零元素个数为 20 到 100 的范围内与aLASSO-SBL 算法接近,但是在非零元素个数增加到 1 20 时准确性低于FaLASSO-SBL 算法.图12 为高维信号复值模型下的稀疏恢复准确度与稀疏度之间的关系.观察图12,HSL-SBL 算法和本文提出的aLASSOSBL 算法在非零元素数目为 20 到 1 20 范围内的稀疏恢复准确性优于现有算法,但是HSL-SBL 算法在非零元素数目大于 1 20 时失效.本文提出的FaLASSO算法稀疏恢复准确性优于除aLASSO-SBL 算法和HSL-SBL 算法之外的其它算法,但计算复杂度低于aLASSO-SBL 算法和HSL-SBL 算法. 本次仿真实验研究各个算法稀疏恢复性能和信噪比的关系.对于实值信号模型,测量矩阵的维度设置为 100×200,即测量数为 100,信号长度为 2 00.信号中非零元素个数设置为 50.SNR 变化范围为10 dB 到30 dB,间隔为5 dB.独立实验次数为200次.复值信号模型参数设置与实值信号模型相同.对于实值信号模型和复值信号模型的稀疏信号恢复结果分别如图13 和图14 所示. 图13 实值模型下各算法稀疏恢复准确度与信噪比的关系Fig.13 RMSE of different algorithms versus SNR with the real-value signal model 图14 复值模型下各算法稀疏恢复准确度与信噪比的关系Fig.14 RMSE of different algorithms versus SNR with the complex-value signal model 由图13 可知,当SNR 小于20 dB 时,所有算法失效,即信号几乎不能被恢复.当SNR 大于20 dB时,所有算法的稀疏恢复准确性随SNR 的提高而提高.其中,本文提出的aLASSO-SBL 和FaLASSO-SBL 算法在SNR 大于20 dB 时恢复效果优于其他算法. 如图14 所示,对于复值信号模型,当SNR 低于15 dB 时,所有算法恢复效果比较差,HSL-SBL在SNR 为10 dB 的情况下出现不收敛的情况.当SNR 大于15 dB 时,所有算法的RMSE 随SNR 的增加而降低,而本文提出的aLASSO-SBL 和FaLASSO-SBL 算法恢复信号的RMSE 比其它算法低. 与仿真二和仿真三相同,为验证本文提出算法对高维信号的恢复性能,进行如下实验.对于实值信号模型,信号长度设置为2000,测量数设置为200,非零元素数设置为100.SNR 变化范围为15到35,间隔为5 dB.独立实验次数为200 次.对于复值信号模型,SNR 变化范围为10 到30,其它参数设置与实值信号模型相同. 图15 为高维实值信号模型下各算法稀疏恢复准确度与信噪比的关系.观察图15,所有算法的恢复准确度随着SNR 的增大而提高,本文提出的aLASSO-SBL 算法和FaLASSO-SBL 算法在SNR为20 dB 到35 dB 的范围内恢复的准确率优于现有算法. 图15 高维实值信号模型下各算法稀疏恢复准确度与信噪比的关系Fig.15 RMSE of different algorithms versus SNR with the high-dimensional real-value signal model 图16 为高维实值信号模型下各算法稀疏恢复准确度与信噪比的关系.观察图16,HSL-SBL 算法、aLASSO-SBL 算法和FaLASSO-SBL 算法在SNR为20 dB 到30 dB 的范围内恢复的准确率优于现有算法,但是HSL-SBL 算法在SNR 低于20 dB 时失效. 图16 高维复值信号模型下各算法稀疏恢复准确度与信噪比的关系Fig.16 RMSE of different algorithms versus SNR with the high-dimensional complex-value signal model 波达方向(Direction of arrival,DOA)估计是稀疏恢复的应用之一.通过预定义网格构建测量信号的空间中的过完备表达模型,将DOA 估计问题可转换为稀疏信号恢复问题[15].其中,恢复的信号的非零元素对应的位置代表信号源的到达角.使用单个快拍的测量数据进行DOA 估计的方法称为单快拍DOA 估计.本小节将结合单快拍DOA 估计验证提出的算法的性能. 本小节中使用的所有算法总结如下:SS-ESPRIT 算法为文献[36] 中提出的针对单快拍条件下DOA 估计的空间平滑ESPRIT 算法;L1-SR 算法为文献[37]中提出的基于ℓ1范数的单快拍DOA估计算法;SURE-IR 算法为文献[38]中提出的超分辨算法;OGSBL 为文献[39]提出的基于SBL 的离网格DOA 估计算法;HSL-SBL 为文献[19]中提出的基于合成LASSO 先验的SBL 算法;aLASSOSBL 算法和FaLASSO-SBL 算法为本文中提出的算法.其中,HSL-SBL 算法、aLASSO-SBL 算法和FaLASSO-SBL 算法需采用文献[39]中的离网格方法对估计的方位角进行提纯. 其中,NMC表示Monte-Carlo 实验的次数,设置为200;θi表示第i次Monte-Carlo 实验的声源实际方位角;表示第i次Monte-Carlo 实验的估计的声源方位角.本次仿真分别测试各个算法在不同测量数(阵元数)和不同SNR 下的DOA 估计准确性.结果分别如图17 和图18 所示. 图17 DOA 估计的准确度与测量数的关系Fig.17 RMSE of DOA estimation using different algorithms versus number of measurements 图18 DOA 估计准确度与信噪比的关系Fig.18 RMSE of DOA estimation using different algorithms versus SNR 图17 为不同测量数下DOA 估计准确度的结果.其中,SNR 设置为20 dB.如图所示,HSL-SBL算法和本文中提出的aLASSO-SBL 算法在测量数为 20 到 50 的范围内DOA 估计准确性优于其余算法,但是HSL-SBL 算法在测量数小于 20 时失效.与HSL-SBL 算法和aLASSO-SBL 算法相比,FaLASSO-SBL 算法的准确性有所下降,原因是阵列流形矩阵中的列向量在测量数小的情况下相关性较高[15],导致FaLASSO-SBL 算法性能下降.但是当测量数增大M ≥30 时,本文提出的FaLASSO算法准确性优于OGSBL 算法、L-SR 算法和SUREIR 算法. 图18 为不同SNR 下DOA 估计准确度的结果.其中,测量数设置为 50.如图所示,HSL-SBL 算法和本文中提出的aLASSO-SBL 算法在SNR 为10 到 30 的范围内的DOA 估计准确性优于其余算法,但是HSL-SBL 算法在SNR 小于 10 时失效.与HSLSBL 算法和aLASSO-SBL 算法相比,FaLASSOSBL 算法的准确性有所下降. 表3 给出了SNR 为20 dB,测量数为 50 时各单快拍DOA 估计算法单次运行时间.结合图17 和图18 可知,相比于HSL-SBL 算法,本文提出aLASSO-SBL 算法在不增加计算量的前提下提高了算法的稳定性,在小测量数或低信噪比的情况下性能优于HSL-SBL 算法.而本文提出的FaLASSOSBL 算法在运算速度方面具有优势. 表3 单快拍DOA 估计实验各算法单次运行时间Table 3 Time consumptions of different algorithms for single snapshot DOA estimation 下面对实验结果进行总结.通过图5、图6、图7和图8 可知,在相同测量数下,本文提出aLASSOSBL 和FaLASSO-SBL 算法稀疏恢复准确性优于现有算法.另外,比较表1 和表2,当信号维度增加时,本文提出aLASSO-SBL 算法的计算量会明显提高,本文提出的FaLASSO-SBL 算法对高维信号进行恢复时,在计算量方面比aLASSO-SBL 算法有明显优势.根据图9、图10、图11 和图12 可知,aLASSO-SBL 和FaLASSO-SBL 算法鲁棒于信号的稀疏度,即在稀疏度比较低的情况下仍然可以精确的恢复出信号.根据图13、图14、图15 和图16可知,本文提出的LASSO-SBL 和FaLASSO-SBL算法的在高SNR 的条件下信号恢复准确性比其它常用算法高. 对于单快拍DOA 估计而言,由于单快拍DOA估计中阵列流型矩阵的列向量具有在测量数较少时相关性较高,所以导致FaLASSO-SBL 算法在小测量数时(M ≤20)性能下降.根据图17 和图18 可知,当测量数较大时,本文提出的aLASSO-SBL 算法和FaLASSO-SBL 算法的单快拍DOA 估计准确性优于现有单快拍DOA 估计算法,结合表3 可知,本文提出的FaLASSO 算法降低了aLASSO-SBL算法计算量.综上所述,当测量矩阵A的列向量不相关时,aLASSO-SBL 算法的稀疏恢复准确度优于现有算法,FaLASSO-SBL 算法的准确度略低于aLASSO-SBL 算法但是计算量明显低于aLASSOSBL 算法;当测量矩阵A的列向量相关时,FaLASSOSBL 算法的稀疏恢复准确度有明显下降.对于单快拍DOA 估计而言,在测量数大的情况下FaLASSOSBL 算法准确性和运算速度优于现有算法. 针对稀疏信号恢复问题,本文提出了两种SBL算法,即aLASSO-SBL 算法和FaLASSO-SBL 算法.其中,FaLASSO-SBL 算法是aLASSO-SBL 算法的快速算法.具体的创新点为:1) 提出一种多层先验的稀疏贝叶斯框架用于稀疏贝叶斯模型构建,赋予信号中元素独立的LASSO 先验.通过分析,自适应LASSO 先验比现有稀疏先验更有效的鼓励稀疏.根据构建的稀疏恢复模型提出了aLASSOSBL 算法.2) 在贝叶斯推断阶段,利用空间轮换方法避免矩阵求逆运算,进一步降低了算法的计算复杂度,使参数更新快速高效.从而提出了FaLASSOSBL 算法.本文提出的算法的稀疏恢复性能通过仿真实验进行了验证,结果表明本文提出基于自适应LASSO 先验的SBL 算法比现有算法具有更高的稀疏恢复准确度;本文提出的快算法的准确度略低于基于自适应LASSO 先验的SBL 算法,但计算复杂度明显降低.对于单快拍DOA 估计而言,在测量数大的情况下FaLASSO-SBL 算法准确性和运算速度优于现有算法. 附录A Woodbury 引理.如果矩阵A、矩阵C和矩阵C−1+V A−1U是非奇异矩阵,则有以下恒等式: 其中,矩阵A、矩阵C、矩阵U和矩阵V为维度合适的矩阵.4 仿真实验

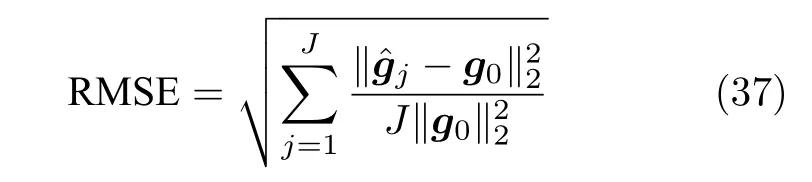
4.1 仿真实验一

4.2 仿真实验二



4.3 仿真实验三




4.4 仿真实验四



4.5 单快拍条件下波达方向估计实验验证



4.6 仿真结果分析总结
5 结论


