立足自主探究的小学数学概念教学策略探索
——以人教版五年级下册“体积和体积单位”教学为例
林来城
(漳州市长泰区林墩中心小学,福建 漳州 363904)
数学概念是人们对现实对象的数量关系和空间形式的本质特征的思维反映形式。教师应提供充分的感性材料,创设各种数学活动,引导学生在自主探究中,经历直观感知、抽象概括、建立表象的过程,并在具体应用中理解、掌握、深化概念。[1]本文以人教版小学数学五年级下册第三单元“体积和体积单位”一课为例,探讨基于自主探究的数学概念教学策略。
一、实验操作探究,感知数学概念
由于数学概念的严谨性和抽象性,加上小学生以形象思维为主的特点,数学概念并不容易被小学生理解接受。因此,教师需要为学生提供感性材料,让学生亲历实验操作探究的活动。学生在操作、观察、对比中发现问题、提出问题、思考问题、研究问题,让数学概念的形成由具体感知到理性认识,从而建立完整表象。例如,在教学“认识体积”的环节时,教师创设并引导学生在实验操作中观察、发现、思考、交流、感知体积概念。
师:在每个小组的桌上都有两个相同的量杯、一小桶水、一个小土豆和一个大鹅卵石。这节课,我们要先用这些器具来做个实验。(屏幕出示实验要求)

生1:我们发现,把小土豆和大鹅卵石放入水中,水面就上升了;两个量杯中水面上升的高度不一样,放入大鹅卵石那杯水的水面上升得比较高。
师:这是为什么?可以得到什么实验结论?
生2:小土豆和大鹅卵石放入水中,把水的位置占了,把水往上挤,所以水面会升高。
师:小土豆和大鹅卵石所占的位置,叫作它们所占的空间。
生3:大鹅卵石比小土豆大,占的空间就大,所以放入大鹅卵石那杯水的水面上升得比较高。
生4:物体占有空间,不同物体所占的空间大小不同。
(屏幕出示:冰箱、电视机、手机的图片)
师:谁能比划出这三个物体所占的空间?哪个物体所占的空间最大,哪个物体所占的空间最小?
生5:冰箱所占的空间最大,手机所占的空间最小。
师:物体所占空间的大小就叫作物体的体积。冰箱所占的空间最大,手机所占的空间最小,我们就说冰箱的体积最大,手机的体积最小。
教学中,通过组织学生进行实验操作探究,发现把小土豆和大鹅卵石放入装水的量杯中,水面会上升。由于小土豆和大鹅卵石的大小不同,水面上升的高度不同,将抽象的“空间”转化为具体的形象。接着,通过比划、比较不同物体所占空间的大小,使体积的概念在不断地感知中自然抽象、归纳出来。学生在实验操作中感知,在对比中生成,初步认识体积的立体形象。
二、小组合作探究,建构数学概念
数学概念的学习,应全面调动学生的积极性、主动性、创造性,让学生经历概念的建构过程。学生是生动活泼、富有个性的个体,小组活动探究能让学生在教师精心组织和指导下,在核心问题引领下,积极思考、动手操作、合作交流,在充分发挥个人能力与小组成员的互助中,探究、解决问题,深度建构概念。例如,在“建构体积单位概念”的环节中,教师引导学生回顾长度单位、面积单位及计量对象后,组织四人一组的小组合作探究活动。以1cm3教学为例,屏幕出示探究要求:

师:如图1,怎样比较这两个长方体体积的大小呢?请小组合作讨论,制定方案。
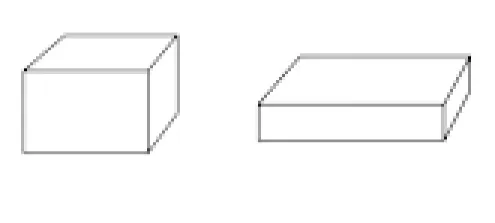
图1
小组1:可以在两个量杯中倒入相同的水,然后把两个长方体分别浸没在水中,哪个杯子水面上升得高,哪个体积就大。
小组2:如果这两个长方体很大,量杯就放不下,这个方法行不通。
小组3:如果这两个长方体是纸做的,也不行。
师:那么应该怎么办,才能准确比较呢?
小组4:可以把它们切成相同的小块来比较。
小组5:我们认为,以前度量长度时用到长度单位,度量面积时用到面积单位,现在要比较这两个长方体的体积,也应该有统一的体积单位来度量。
师:你们知道有哪些体积单位吗?
生:立方厘米,立方分米,立方米。
师:什么是1 立方厘米?它是多大呢?请各小组利用学具袋,再次合作探究。(屏幕出示探究要求)

小组1:我们用尺子量出正方体的棱长,棱长是1厘米的正方体,体积就是1 立方厘米。我们感觉1 立方厘米很小。
小组2:我们拿1 立方厘米的正方体和文具盒、书、桌子比,感觉它很小。
小组3:生活中有很多物体的体积接近1 立方厘米,比如骰子、玻璃球、粉笔头等。
师:1 立方厘米的体积单位是指棱长是1cm 的正方体,立方厘米用字母cm3来表示。
师:怎样用立方厘米的体积单位,比较出这两个长方体的体积大小呢?请小组再次合作探究,解决问题。(屏幕出示探究要求)

小组1:我们用1cm3的小正方体摆出这两个长方体,左边的用了12 个,右边的用了15 个。所以右边的长方体体积大。
小组2:我们是用1cm3的小正方体去量的,左边长方体的长是3 个小正方体的棱长,宽和高是两个小正方体的棱长,所以有12 个小正方体。右边长方体的长、宽、高分别是5 个、3 个、1 个小正方体的棱长,所以有15 个小正方体。所以右边长方体的体积大。
小组3:我们先分别测量出两个长方体的长、宽、高,左边长方体的长、宽、高分别是3cm、2cm、2cm,右边长方体的长、宽、高分别是5cm、3cm、1cm。再把每个面分成一个个边长为1cm 的正方形,发现可以把两个长方体分成许多棱长是1cm 的小正方体。左边的长方体可以分成12 个棱长为1cm 的小正方体,右边的长方体可以分成15 个棱长为1cm 的小正方体,所以右边的长方体体积大。
学生汇报后,教师用动画演示测量的过程(如图2):
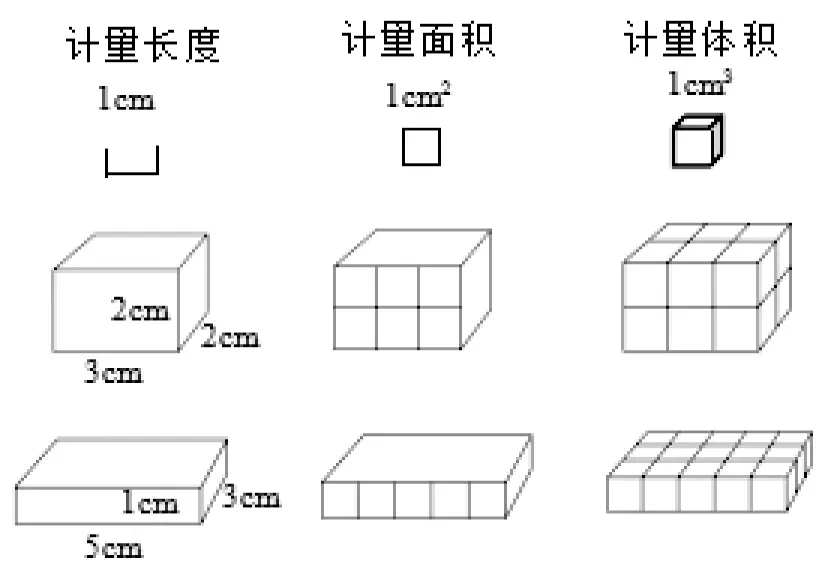
图2
师:经过演示,我们知道测量不同的对象,应该有不同的单位。测量体积要用体积单位。左边的长方体有12 个1cm3,所以体积是12cm3;同理,右边的长方体体积是15cm3,所以右边长方体的体积大。
教学中,教师以核心问题为引子,组织学生多次进行小组合作探究。先创设比较两个长方体体积大小的问题,引导学生借鉴以往的学习经验,类比迁移,引出体积单位;再通过想一想、摸一摸、找一找等探究活动,认识1cm3;最后运用1cm3体积单位,度量出两个长方体的体积,并通过动画的计量演示,帮助学生感知长度单位、面积单位、体积单位的区别与联系。在小组合作探究中,学生积极思考、团结协作、发挥潜能、体验成功,既掌握从一维到三维的度量概念、方法,也深度建构1cm3的体积单位概念,发展空间观念,将体积单位的三维性扎根于心中。[2]
三、精练拓展探究,深化数学概念
教师要根据学生的实际学情,准确把握“了解、理解、掌握、运用”不同层次的要求,精心设计针对性、灵活性、多样性的练习。根据习题的难易程度,引导学生通过自主探究、讨论交流、实践操作等方式解决问题,进而深化概念,最终构建新的知识系统。例如,在“巩固应用”环节,为了加深学生对体积单位的理解和掌握,提升应用能力,教师设计如下练习。
1.慎思细选。请对题目中的实际物体进行探究,选出正确答案。
(1)下列物体的体积,接近16 立方分米的是( )。
A.书包 B.橡皮擦 C.字典 D.小货车
生:A。因为橡皮擦的体积很小,只有几立方厘米。我测量了字典,长和宽大约是1 分米,高只有0.3分米,所以体积不到1 立方分米。小货车的体积很大,应该是16 立方米。书包的体积最接近16 立方分米。
(2)下列物体都是用棱长1cm3的小正方体拼成的,( )的体积是6cm3。

生:C。因为只要数出每个物体有几个1cm3,就可以知道它们的体积。C 是由6 个小正方体组成的,所以体积是6cm3。
2.辨析纠正。在生活中,要正确地使用各种单位名称,否则会闹出笑话。请读一读小马虎写的这篇日记。

师:请同学们先自己找出不合理的地方,尝试修改,然后在小组内讨论交流,说一说错误的原因。
生1:新房子有128m。m 是长度单位,是一条线,怎么住人呢?房子的面积应是128m2。
生2:大货车的车厢约有20cm3。20cm3只有1 个鸡蛋那么大,怎么装东西呢?车厢体积应是20m3。
生3:液晶电视有19m3。教室的讲台大约1m3,19 m3就是19 个讲台,房间怎么放得下呢?液晶电视的体积应是19dm3。
生4:每个汤圆有1dm3,和粉笔盒一样大。每个汤圆应是1cm3。
师:请仔细观察,小组合作探究解决问题。
生1:我是用拼的。再放5 个小正方体,就可以拼成棱长2cm 的大正方体。我数了数小正方体,一共有8 个,所以拼成的大正方体的体积是8cm3。
生2:我观察原图,它的长边是2cm,所以拼成的大正方体的棱长是2cm,一共要8 个小正方体,体积是8cm3。图中原有3 个小正方体,所以至少还需要5个小正方体。
教师充分挖掘素材,抓住知识的重难点,精心设计练习,引导学生应用各种探究方式解决问题。学生在比较选择中,巩固感知各种体积单位以及计量物体体积的方法;在结合生活实际的辨析纠正中,对长度、面积、体积等各种单位产生更深的理解;在思维拓展活动中,发展空间想象能力,提升思维品质,使所学知识转化为能力。这样,学生在轻松愉快的练习中,获得成功的体验,加深对数学概念的认知。
四、结语
总之,对于数学概念教学,教师要提供充分的感性材料,创设丰富的数学活动,引导学生在主动探究的过程中获得感知、经历建构、应用深化,从而掌握本质属性,为后续的学习打下坚实的基础。

