空气自由场装药爆炸荷载一维建模数值算法

杨允锴， 武双章， 高振儒， 毛益明

（ 陆军工程大学野战工程学院， 江苏 南京 210007）

0 引言

当下结构与构件的抗爆性能及防护研究任务仍旧繁巨，然而结构与构件爆炸试验成本昂贵，且安全风险大，因此数值模拟已成为爆炸研究领域的有效手段。准确可靠的爆炸荷载计算，是分析结构爆炸响应和毁伤评估的基础与关键。如何利用数值模拟软件准确计算爆炸荷载并模拟空气冲击波传播过程，是进行结构抗爆研究的首要问题。

关于自由空气中TNT 炸药爆炸荷载的计算，已有不同学者得出一些预测方法及经验公式， 虽然已经广泛应用于结构爆炸响应分析和构件损伤评估的研究中， 但采用不同方法计算结果存在较大差异。 在有限元分析软件LS-DYNA 中，爆炸荷载的施加主要有三种方式：第一种是三角形冲击荷载，该方法计算效率最高，建模简单，但此法无法模拟爆炸荷载的非均布加载， 也无法模拟空气冲击波与构件相互作用的问题， 因此得到的误差较大； 第二种是CONWEP 法，即通过*LOAD_BLAST、*LOAD_SEGMENT_SET 和*DEFINE_SEGMENT 等关键字来施加一些特定的爆炸荷载，此法可以略过炸药与空气建模步骤，简化建模流程、提高计算效率， 但无法考虑空气冲击波反射及绕射等现象，仅适于远距离爆炸下结构的动态响应分析；第三种是流固耦合法，建立空气域和炸药模型，直接模拟炸药爆炸过程、空气冲击波传播过程以及冲击波荷载加载过程，因此考虑了空气冲击波与目标结构的相互作用， 效果最为准确直观，缺点在于网格尺寸、初始条件对计算精度影响大，建模复杂、计算效率低[1]。 姚成宝[2]通过研究得出保证三维流固耦合法计算精度的两个结论： ①为保证爆炸荷载计算精度，空气网格划分应小于2mm；②空气域模型的尺寸至少应为构件尺寸的2 倍以上， 以消除无反射边界条件的影响。因计算机性能限制，以上两点结论很难在结构与构件毁伤数值模拟研究中实现。

为解决采用三维流固耦合法开展构件毁伤数值模拟时计算效率低下、计算误差大的问题，首先利用有限元分析软件LS-DYNA 建立装药爆炸与空气冲击波一维仿真模型， 计算了6.82g 和1000g 球形TNT 装药在自由空气中爆炸的空气冲击波超压值， 并分别与经验公式计算结果、三维模型计算结果[3]进行了对比，结果表明利用一维仿真模型计算爆炸荷载计算效率与计算精度更高。 再按照“两步法”将一维仿真模型的计算结果映射到三维，进一步模拟空气冲击波传播并毁伤构件的过程。 实际算例表明，“两步法” 能够在保证计算效率与计算精度的前提下，模拟空气冲击波与构件的相互作用过程，在结构与构件抗爆领域具有广泛的应用前景。

1 爆炸荷载工程算法

关于球形TNT 装药自由空中的爆炸荷载计算，已有学者进行了大量的相关研究， 并获得了可信度较高的成果。爆炸荷载主要用冲击波压力、峰值超压、比冲量、持续时间、到达时间等冲击波参数来描述，其中冲击波超压是研究结构与构件毁伤的重要参数。 冲击波超压通常用比例距离来表达。 比例距离可以定义为：

贝克（W.E.Baker）[6]通过实验得到的经验公式是：

式中：F—冲击波到达时间ta， 自由空中爆炸时冲击波的峰值超压ΔPm及正压作用时间t+等参数；A、B、C、D、E、F、G—对应的实参数系数，具体取值见表1；其余参数与式（2）相同。

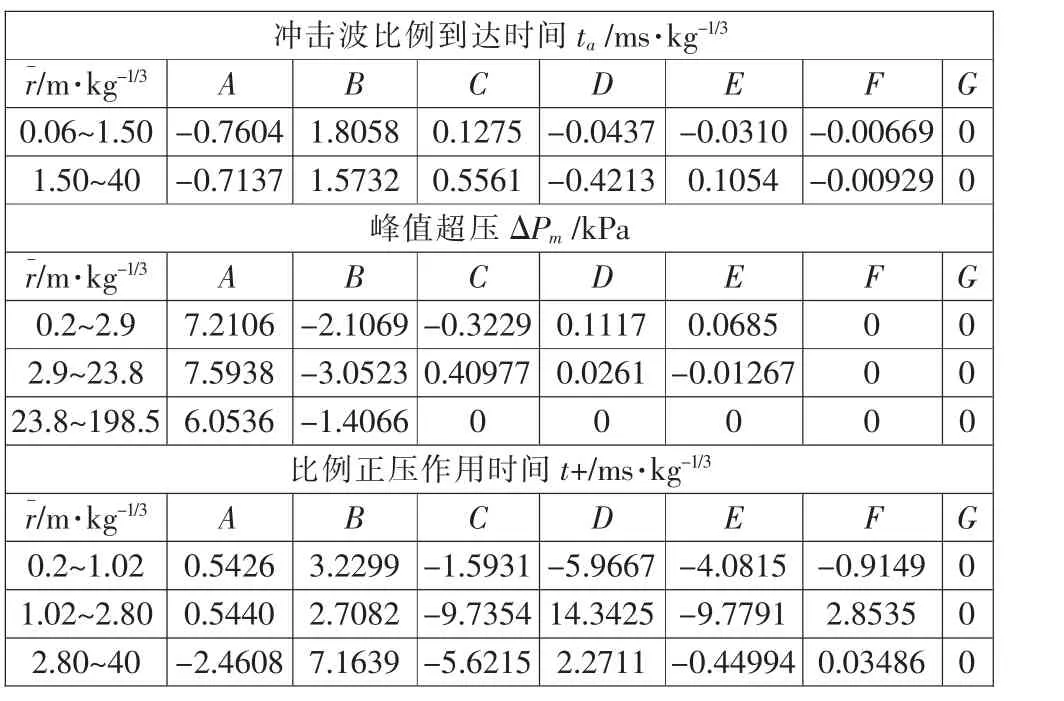
表1 简化的Kingery 空气冲击波参数Tab.1 Shock wave parameters of simplified kingery formula

为了将不同经验公式的预测结果进行直观的对比，在对数坐标系中给出各经验公式预测的峰值超压值随比例距离的变化关系，见图1。

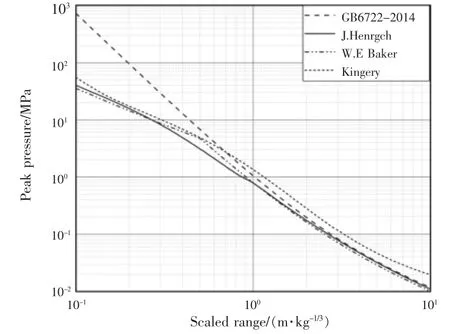
图1 不同经验公式冲击波峰值超压-比例距离对比图Fig.1 Comparison of peak pressure attenuation against scaled distance

从图中可以看出，在比例距离较小时，式（3）～（5）的计算结果接近，而式（2）因超出公式适用范围，计算结果偏差偏大；随着比例距离增大，式（2）～（4）结果趋于一致，但式（5）主要用于为结构抗爆设计提供参考，计算结果偏大。 通过比较，式（3）整体范围内计算结果均处于可信范围，因此本文将亨利奇公式作为推荐公式，将其计算结果与仿真计算结果进行对比。

2 一维仿真模型

选用大型通用显式有限元分析软件LS-DYNA 建立球形TNT 装药在自由空中爆炸的一维仿真模型，模拟空气冲击波传播并计算爆炸荷载。

2.1 物理模型

在建立一维模型时，使用BEAM161 梁单元建立TNT炸药和空气物理模型， 模型采用cm-g-μs 单位制。 为便于将计算结果与三维模型[3]进行对比，TNT 药量确定为6.82g 和1000g 两种工况。

针对2 种不同工况，分别建立相应的一维仿真模型。工况一的TNT 装药模型长度1cm，空气域模型长度200cm；工况二中TNT 装药模型长度5.3cm， 空气域模型长度2000cm。TNT 与空气两种材料之间采用共节点接触，并划分为1mm均匀网格， 分别在比例距离为0.1、0.5、1、2、3、4、5、6、7、8m/kg1/3位置处设置追踪点，物理模型见图2。

图2 一维模型示意图Fig.2 The one-dimensional model

2.2 材料模型与状态方程

TNT 炸药选用008 号材料模型*MAT_HIGH_EXPLOSIVE_BURN，其具体材料参数在表2[9]中给出。爆炸力学中用状态方程来描述爆轰产物系统中各物理量（压力、体积、温度等）之间的关系，在进行一维数值模拟时选用*EOS_JWL 状态方程， 该方程定义压力为相对比容V 和爆轰产物比内能e 的函数：

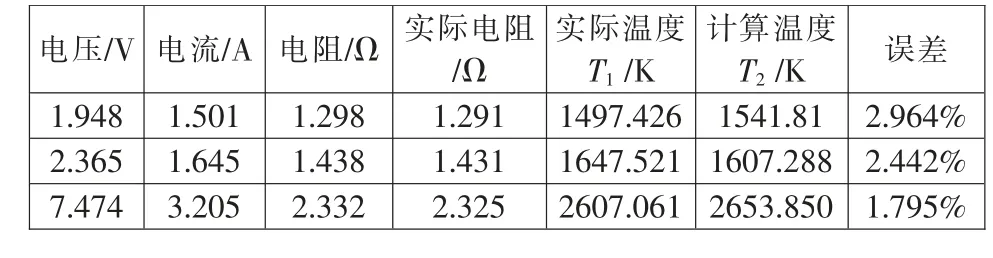
表2 反演验证计算结果

表2 TNT 炸药材料模型参数Tab.2 Parameters of TNT model parameters

表3 JWL 状态方程参数Tab.3 Parameters of the*EOS_JWL

采用009 号材料模型*MAT_NULL 以及线性多项式状态方程*EOS_LINEAR_POLYNOMIAL[9]描述空气的材料特性，线性多项式状态方程表述为：

式中：c0～c6—与空气性质有关的常数；pa—空气的压力；μ—相对密度，μ=ρ/ρ0-1，ρ、ρ0分别为空气的密度、 初始密度；E0，a—空 气 的 初 始 体 积 内 能。 空 气 的 初 始 密 度 取0.00125g·cm-3，状态方程中具体参数取值见表4[10]，其中V0为初始的相对体积。

表4 LINEAR_POLYNOMIAL 状态方程参数Tab.4 Parameters of the*EOS_LINEAR_POLYNOMIAL

2.3 仿真计算与数据分析

通过*SECTION_ALE_1D 定义一维模型的欧拉算法，并使用Van Leer+HIS（二阶精度）方法进行计算，以应对炸药与空气网格的严重畸变。 2 种不同工况的求解时间 分 别 为30000μs 和90000μs。 利 用 后 处 理 软 件Ls-Prepost 对仿真结果进行处理和分析， 得到各追踪点位置处空气冲击波的计算结果， 并绘制了工况二中比例距离和比例距离处的冲击波压力时程曲线，分别如图3（a）和图3（b）。

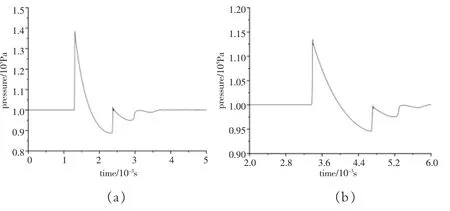
图3 工况二不同位置处压力时程曲线Fig.3 Overpressure response time history of condition two

将2 种工况条件下数值模拟的计算结果与亨利奇公式的计算结果进行对比， 并得到其相对误差， 具体见表5。可以看出2 种工况下数值模拟计算结果与经验公式预测值均存在一定误差，且比例距离时误差较大。主要原因在于推导经验公式的实验数据误差。 空气中TNT 爆炸冲击波近场参数测量难， 早先的工程算法研究的试验装置灵敏度和精度不够理想，造成试验数据误差，使得经验公式预测值存在一定偏差。

2.3.1 经验公式计算值对比

通过对表5 空气冲击波压力值计算结果的对比分析，可以发现：数值仿真结果符合爆炸相似原理；2 种工况的最大相对误差值均出现在r=0.1m/kg1/3处， 可见不宜采用数值仿真模拟构件在装药近距离爆炸时的毁伤效果；当比例距离r>0.1m/kg1/3时，各追踪点的数值仿真计算值与亨利奇公式计算值的误差全部均小于20%之内；装药量增加能够减小数值模拟计算值与经验公式预测值的相对误差。

表5 不同比例距离处空气冲击波超压一维仿真模型计算值与经验公式计算值对比Tab.5 Commanded overpressure comparison with simulated overpressure

通过对比可以看出，当比例距离r>0.1m/kg1/3时，一维仿真模型计算的空气冲击波峰值超压误差较小， 符合工程使用要求。

2.3.2 三维模型仿真计算值对比

杨鑫[3]运用LS-DYNA 软件建立三维模型计算球形装药在自由空气中爆炸产生的冲击波超压值， 其三维仿真模型使用的装药药量与本文完全一致， 分别为6.82g和1000g 两种工况，并计算了比例距离0.1、0.5、1、2、3、4、5、6、7、8m/kg1/3处的超压峰值。 两种工况下三维仿真模型计算结果与经验公式计算值的相对误差范围分别为32.2%～94.8%和25.7%～92.9%，而一维仿真模型的两种工况的误差范围分别为-61.3%～12.3%和-43.0%～19.2%。

通过对比可以看出， 一维仿真模型对空气冲击波峰值压力的计算结果与经验公式的预测值相对误差更小，一维模型求解空气冲击波荷载参数的计算精度更高。

3 一维模型计算结果的映射应用

一维仿真模型无法直接模拟空气冲击波与结构构件的相互作用过程，但可以使用“两步法”将一维数值模拟结果映射到三维流固耦合模型中，此时一维模型计算得到的空气冲击波荷载将以三维形式完成对构件的毁伤模拟。

第一步：在进行一维仿真计算时，首先应设置合适求解时间， 使得空气冲击波在求解时间内传播距离大致为装药到达构件迎爆面的距离， 然后在模型求解时生成相应的映射（map）文件。

第二步：建立空气域及构件的三维模型，构件迎爆面方向的空气域尺寸可以减小， 且空气域网格可进行稀疏划分，能够提高计算效率且对荷载计算精度的影响很小。通过*INITIAL_ALE_MAPPING 以及*DEFINE_VICTOR 关键字将map 文件映射至三维模型中， 并定义映射起始点及方向，此时空气冲击波荷载将在三维模型中继续传播。

以装药爆炸毁伤钢板为例，验证两步法的可行性。将第2 节中1000g 球形TNT 装药爆炸的一维仿真结果，映射到建立的空气和钢板所在三维模型， 其中空气域尺寸1200mm×1200mm×500mm，钢板尺寸1000mm×1000mm×2mm，两者采用流固耦合法模拟相互作用关系。 映射方向为钢板迎爆面法线的负方向， 映射点为钢板中心点在空气域表面的正投影点，三维模型及映射关系见图4。

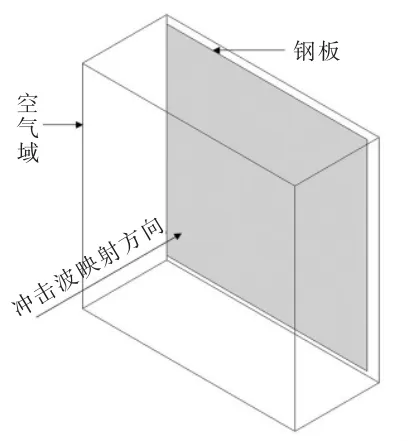
图4 三维模型及映射关系图Fig.4 3D model andmapping relationship

由图5 可以看出， 冲击波实现了在三维模型中的映射与传播， 并对构件造成了毁伤。 可见“两步法”在保证冲击波荷载计算精度和计算效率的前提下，准确模拟冲击波与构件的相互作用过程。

图5 钢板毁伤图Fig.5 Damage effect of steel plate

4 结论

通过建立一维模型进行球形TNT 炸药自由空气中爆炸工况的数值模拟研究， 对比经验公式计算值和前人所做三维数值模拟结果，得出以下结论：

现有的空中TNT 爆炸冲击波荷载的经验公式有很多， 但不同学者的经验公式预测结果存在一定的适用范围及差别。研究近爆作用下构件毁伤效应时，亨利奇公式的预测结果更加准确。

通过对比一维仿真模型、 三维仿真模型获得的空气冲击波超压值与经验公式预测值的相对误差， 可知一维仿真模型的计算结果误差更小， 即采用一维模型求解爆炸空气冲击波荷载时计算精度更高。 其原因在于数值模拟计算装药爆炸荷载时， 网格尺寸能够显著影响求解精度，网格尺寸越大，误差就越大，网格尺寸小于2mm 时计算精度能够得到保证； 而三维模型的网格尺寸减小会导致计算效率的大幅下降，受计算机性能的限制，实际应用中难以实现。“两步法” 是将一维模型计算所得高精度空气冲击波荷载映射到三维模型中，并模拟其与构件的相互作用的一种方法。 利用“两步法”能够把一维模型建模简单、计算精度高、计算效率高的优点，与三维流固耦合模型真实模拟空气冲击波与构件相互作用过程的优点相结合，为结构与构件爆炸毁伤研究提供了一种高效的数值模拟方法。