新型移动配重动臂塔机平衡臂结构设计与仿真分析

刘士明， 桂召健， 赵 欣

（1.沈阳建筑大学 机械工程学院， 辽宁 沈阳 110168； 2.抚顺永茂建筑机械有限公司， 辽宁 抚顺 113126）

0 引言

动臂塔式起重机具有起升高度大、起重量大、平衡臂短等优点，在建筑施工中得到了广泛的应用。 随着动臂塔机起重量的增大，起平衡作用的配重重量随之增大，导致塔机空载工况和最大幅度满载工况时前后力矩差增大，从而使塔身和基础受力增大。 为了改善这种情况，贾林昕等[1]提出了一种曲柄摇杆滑块式移动配重，配重悬挂于平衡臂轨道上，吊臂通过连杆结构与配重连在一起，当工作幅度由大变小时，配重从远离回转中心的一端向回转中心方向移动。屠凤莲等[2]提出了平行四边形连杆结构移动配重，配重通过摇杆绕平衡臂某定点转动， 曲柄与吊臂固定连接，当吊臂幅度改变时，配重重心相对摇杆定点摆动。 王新聪等[3]提出了一种油缸变幅动臂塔机移动配重机构，配重、平衡臂与起重臂刚性连接，配重、平衡臂、吊臂可绕吊臂与回转平台的铰接点转动，油缸来控制吊臂俯仰摆动。 上述三种结构均利用吊臂幅度改变，通过连杆结构改变配重的力臂，这些结构的主要缺点在于移动配重只能平衡吊臂角度变化引起的力矩改变， 无法考虑吊重变化引起的力矩变化。秦剑等[4]提出了一种新型摇动平衡臂设计方案，该方案使平衡臂在变幅机构的作用下绕回转平台上下转动，以此改变配重的力臂，但该方案不利于塔机起升机构、变幅机构的布置、检修等。

随着计算机技术的普及和有限单元法的发展， 出现了大量的有限元仿真软件， 应用有限元分析软件进行复杂结构的仿真分析， 省时省力的同时提高了计算效率和精度。靳龙等[5]对塔机吊臂进行了静力分析和线性屈曲分析，依据分析结果调整吊臂杆件的截面尺寸，结果表明改进后的吊臂刚度和稳定性良好；花园等[6]对塔机整体结构进行了多工况静力分析， 给出了不同工况下塔机的危险部位，确定材料属性、外部载荷、最大起重量、钢结构截面尺寸等对起重机的影响；金玉萍[7]利用ANSYS APDL 语言建模，对塔机整体进行静力分析，并提取相关节点应力值与实际塔机检测结果进行对比，结果显示ANSYS 分析的结果是可靠的；姚克恒等[8]利用ANSYS 对塔机进行建模和有限元分析，以此验证有限元分析方法的正确性，并总结了ANSYS 等效建模等关键技术。

综上所述， 本文提出了一种通过钢丝绳牵引的新型移动配重机构，利用Solidworks 进行三维模型设计，同时对移动配重装置中的平衡臂进行改进，并利用ANSYS 对改进前后的平衡臂进行静力分析和模态分析。

1 平衡臂与移动配重小车设计

新型移动配重动臂塔式起重机顶部结构的三维模型见图1，主要包含人字架、起升机构、变幅机构、A 型架、平衡臂、移动配重小车及其牵引机构，其中移动配重牵引机构包含电机、卷筒、制动器、钢丝绳以及导向滑轮等结构，移动配重可以独立运行。 移动配重4 装于配重小车3 中，配重小车3 悬挂于平衡臂9下翼缘板上，并将其作为导轨进行移动。新型移动配重动臂塔式起重机的实物结构见图2， 目前正在宁波的某施工工地使用。

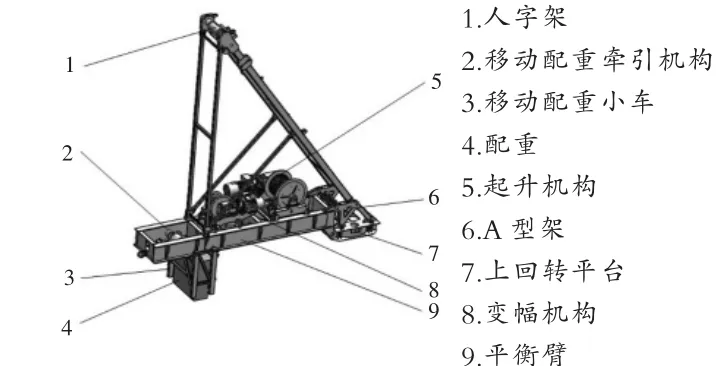
图1 移动配重式动臂塔式起重机顶部结构三维模型

图2 新型移动配重装置实物图

新型移动配重式平衡臂采用双焊接工字梁的形式 见 图3， 长9.86m，宽1.75m，高0.9m，配重可移动的距离为8.28m。 移动配重小车结构见图4，长2.27m，宽1.0m，高2.47m，采用由方管焊接而成的格构式结构。

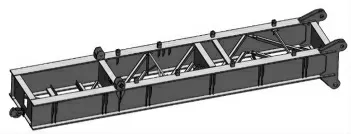
图3 新型移动配重式平衡臂

图4 新型移动配重式配重小车

新型移动配重塔机的工作原理见图5，利用传感器检测塔机的实际起重量，结合吊臂产生的力矩计算出塔机前倾力矩，控制系统自动计算出移动配重所在的位置，移动配重牵引电机驱动配重移动，改变塔机的后倾力矩，以此达到平衡力矩的目的。该方案的优点在于塔机的起升、变幅机构可以直接在平衡臂上安装、检修，并且移动配重可以根据起重量和工作幅度实时调整位置，力矩平衡精度更高。

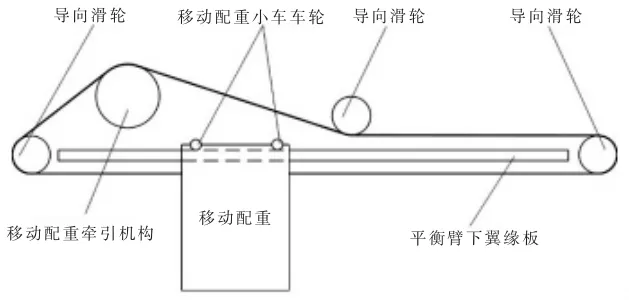
图5 移动配重装置机构简图

2 新型移动配重平衡臂有限元分析

2.1 受力分析

本文针对新型移动配重塔机的平衡臂进行有限元分析，平衡臂承受的载荷主要有移动配重及其牵引机构的重力、变幅和起升机构的重力、人字架后撑杆对平衡臂的拉力以及平衡臂自身的重力， 同时考虑平衡臂平面外的风载。 平衡臂主要承受的载荷大小见表1， 其受力方向见图6。 由于人字架后撑杆的力对平衡臂作用力的方向为竖直向上，有利于改善塔机的受力，因此选择人字架后撑杆的力最小时的工况，即最小幅度空载工况。

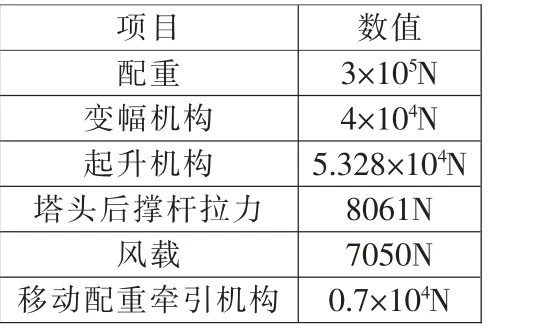
表1 平衡臂载荷施加

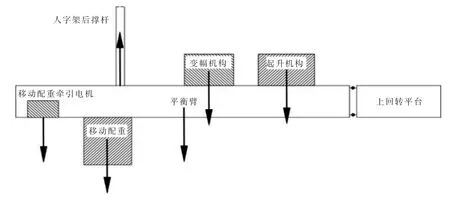
图6 平衡臂受力简图

2.2 有限元模型建立

本文采用ANSYS APDL 建模的方式， 对平衡臂进行参数化建模，其中平衡臂的焊接工字梁、横腹板、耳板以及加强板采用可以承受平面内载荷和法向载荷的Shell 63 单元， 双焊接工字梁之间的腹杆采用基于一阶Timoshenko 梁理论的beam 188 梁单元。 Shell 63 与Beam 188设置基本参数如表2 和表3 所示。

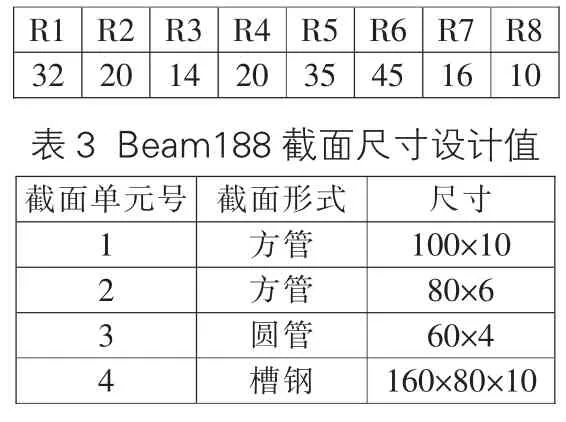
表2 Shell 63 实常数设计值

网格划分采用自由网格划分方式，采用四边形的网格类型，通过对计算精度、计算时间以及网格质量等权衡对比，选择壳单元尺寸为60mm， 划分完成后共生成16267 个单元， 节点数量16516， 根据分析软件计算得到质量为13773.59kg，平衡臂的有限元模型见图7。

2.3 静力分析

根据实际情况，对平衡臂与A 型架连接的销轴添加边界条件，如图7 所示的1～4 号销轴，释放绕销轴的转动，约束其它5 个方向的自由度。移动配重及其牵引机构、变幅及起升机构分别在对应的节点处按图6 所示的位置和表1 所示的数值大小和方向施加载荷；选择平衡臂平面外方向上的所有节点，对其施加平面外风载荷； 对平衡臂施加9.8m/s2的重力加速度。

图7 新型平衡臂有限元模型

对新型移动配重式塔机的平衡臂进行静力分析，分析结果见图8， 最大应力（von Mises stress） 为213.43 MPa，最大应力位置出现在平衡臂工字梁下翼缘板与平衡臂耳板的连接处。 图9为平衡臂腹板结构应力云图，最大应力为49.52 MPa，最大应力位置出现在平衡臂前端腹板的边角处。 平衡臂采用Q345B 钢材， 厚度小于16 mm，其屈服强度为345MPa，平衡臂工字梁上下翼缘板设计厚度为32mm，其屈服极限为295MPa。

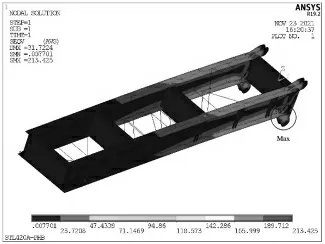
图8 新型移动配重式动臂塔机平衡臂应力云图

图9 新型移动配重式动臂塔机平衡臂腹板应力云图

安全系数γf取1.34，由式（1）计算许用应力为220.15MPa，据图6 所示，平衡臂的最大应力小于许用应力，因此平衡臂满足强度设计。

2.4 模态分析

模态分析主要用来确定结构的某一振动特性， 可以确定结构的固有频率、振型等。 在利用ANSYS 进行模态分析时，需要考虑以下两个假设：

（1）结构刚度矩阵和质量矩阵不会发生改变。

（2）分析时如果不设置使用阻尼特征求解方法，在计算时则不考虑阻尼效应。

通过模态分析， 可在设计结构时有效避免共振或以特定的频率进行振动，避免结构产生较大的损害。在本文中主要采用LANPCG（预条件共轭分块兰索斯法），采用迭代的方法进行求解。

在无阻尼系统中，考虑结构振动方程如下：

鉴于塔机在工作状态和非工作状态平衡臂一直承受配重和各个机构的重量， 因此在进行模态分析时选择考虑平衡臂负载的情况， 将前面静力分析的载荷作为预应力，对平衡臂进行预应力模态分析，提取其前6 阶模态。新型移动配重动臂塔机平衡臂的前6 阶模态见表4。

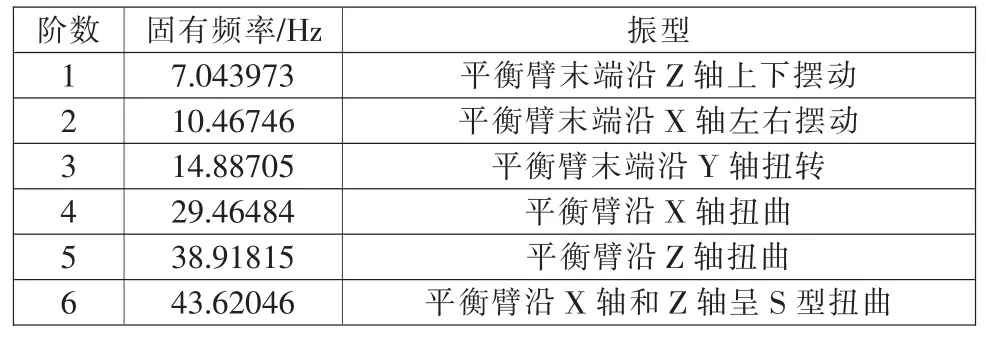
表4 平衡臂前6 阶频率及振型

3 改进移动配重平衡臂有限元分析

根据图9 所示的腹板应力云图，腹板结构受力较小，出现大量的低应力区域，且材料冗余，为减小平衡臂的自重， 减小平衡臂长度方向的风载荷， 将腹板改为组合杆件， 改进前后平衡臂有限元模型的结构对比见图11，改进后平衡臂的质量为13615.87kg，与原平衡臂相比较，质量降低了1.15%，约为157.72kg。

对改进后平衡臂进行有限元分析， 其有限元模型共有节点14704 个，单元14434 个。 对平衡臂进行静力分析和模态分析，改进后平衡臂的应力云图如图12 所示，最大应力为205.34MPa，小于材料许用应力220.15MPa， 应力在允许的范围内。 改进后平衡臂组合腹杆应力云图如图13所示， 最大应力为20.09MPa，最大应力位置出现在平衡臂前端腹杆处， 与图10 所示的腹板应力云图相比较，最大应力位置相同，组合杆件受力更小。

图10 腹板式平衡臂前6 阶振型图

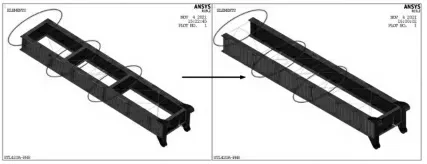
图11 改进前后平衡臂有限元模型对比

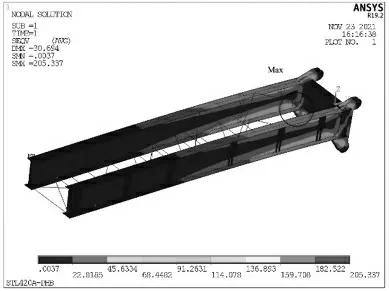
图12 改进后的平衡臂应力云图

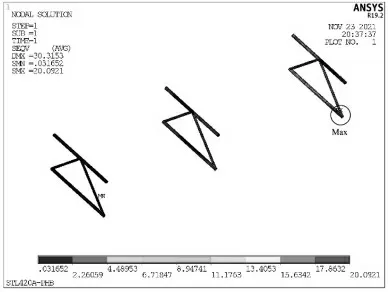
图13 改进后的平衡臂腹杆应力云图

同样将静力分析结果作为预应力，对改进后平衡臂进行模态分析，提取改进后平衡臂的前6 阶模态见图14， 与改进前平衡臂的固有频率对比见表5。

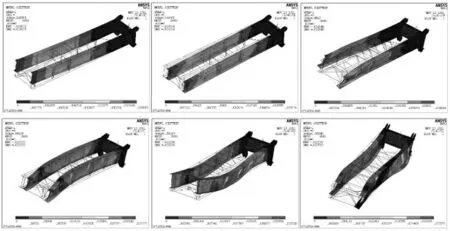
图14 改进后平衡臂前6 阶模态分析振型图

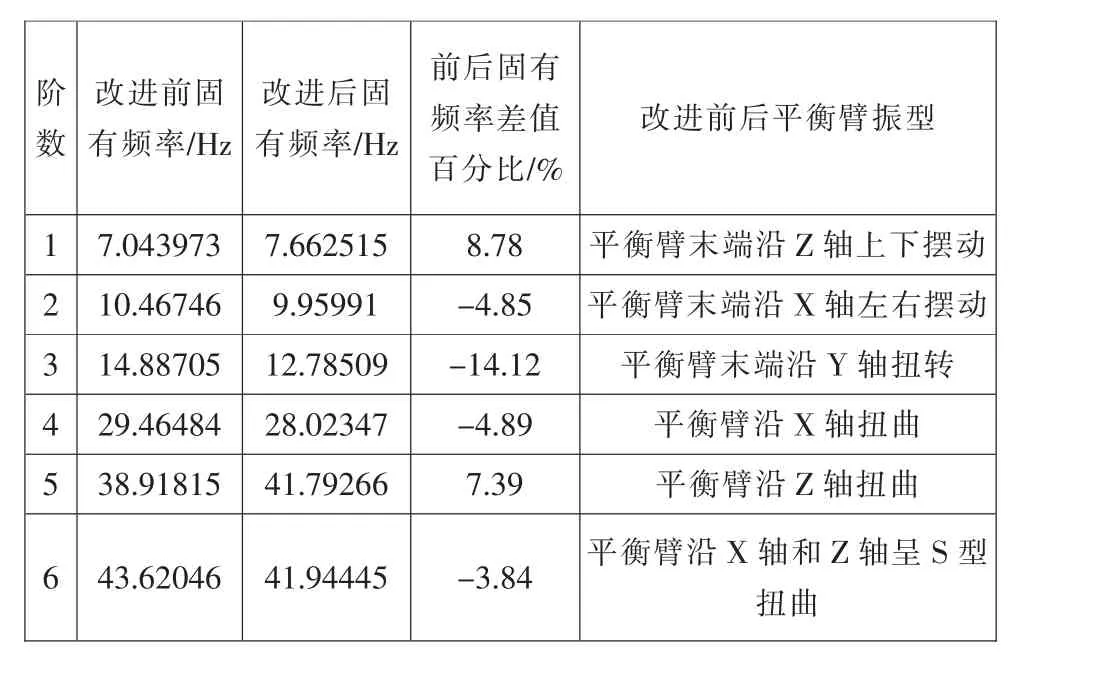
表5 改进后平衡臂前6 阶频率及振型

4 结论

本文设计了一种新型移动配重动臂塔式起重机顶部结构，利用传感器检测吊重大小和工作幅度，通过控制系统实现了移动配重位置的改变，该移动配重实现方式具有非常高的精确性。 同时，设计了新型移动配重塔机的平衡臂，并进行了改进设计，对改进前后平衡臂进行了有限元仿真分析，分析结果表明：新型移动配重塔机改进前后的平衡臂结构都满足强度要求，其整体刚度基本没有变化； 改进后的平衡臂与改进前平衡臂相比，质量降低了1.15%，其前6 阶固有频率略有变化，但振型保持一致。