软刚臂系泊系统多体动力行为模拟和实测验证

童韵， 吕柏呈， 郭冲冲， 武文华,3

(1.大连理工大学 运载工程与力学学部，辽宁 大连 116024； 2.大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116024； 3.大连理工大学深圳研究院，广东 深圳 5180574； 4.中海油研究总院有限责任公司， 北京 100028)

浮式生产储卸油装置属于一种多功能生产系统，具有较强的适应能力，并且储油量大、抗击风浪能力较强，具有灵活转移、循环利用等特征[1]。软刚臂单点系泊系统作为主要的系泊方式之一，广泛地应用于我国的渤海海域。我国首座海洋核动力平台也采用该型系泊系统。受到风、浪、流等荷载的联合作用，在服役过程中曾发生过多起软刚臂单点系泊系统结构破坏的事故。1994年在SZ 36-1油田服役的渤海明珠号由于系泊结构的横摆导致浮式生产储卸油装置船艏与压载舱发生2次碰撞[2]，造成艏部壳体破裂；2011年4月，海洋石油102号浮式生产储卸油装置在服役长达22年后软刚臂系泊系统发生破坏[3]，浮式生产储卸油装置应急解脱，造成油田停产3个多月。以上事故对浮式生产储卸油装置的安全生产造成了严重影响。

近年来，诸多学者开展了对于软刚臂系泊系统的研究工作。詹燕民等[4]对“海洋石油112”号浮式生产储卸油装置软刚臂单点系泊系统进行了系泊分析数值模拟，并与水池实验结果进行对比，验证三维动力响应数值模拟在浅水中应用的准确性。赵梓舒[5]针对软刚臂系泊系统长期受到海洋环境荷载作用，容易出现铰节点损伤的安全问题，基于深度学习的方法，并结合缩比模型试验，对铰节点展开损伤识别研究。张凤伟等[6]对采用软刚臂单点系泊系统定位方式的超大型浮式液化天然气装置开展了风、浪、流联合作用下水动力模型试验研究。肖龙飞等[7]建立软刚臂系泊系统的理论模型以及6自由度静恢复力特性计算分析的数学模型,对软刚臂系泊系统的纵向和横向水平恢复力特性进行数值预报。苏方磊等[8]通过静水衰减和共线风浪流联合作用工况的物理模型试验,对浮式生产储卸油装置各自由度的固有周期和运动响应进行了分析。

现阶段针对软刚臂系泊系统的设计和研究方法主要有模型试验和水动力学分析。考虑到软刚臂系泊系统是一套典型的多铰连接的多体动力学系统，因此还应对其展开多体动力学分析。刘成义等[9]基于多体动力学方法,建立浮式生产储卸油装置-系泊腿-软刚臂的耦合模型,分析了不同水深/吃水比对系泊系统动力响应性能的影响。吕柏呈等[10-11]建立了软刚臂多体动力学方程，构造了系泊系统受到的荷载和各铰节点运动姿态对应的关系，为分析长期服役的系泊系统易损性评估提供了依据。

本文充分考虑了软刚臂系泊系统的铰结构的大尺寸、重载荷的结构特点，对系泊腿、系泊刚臂与单点转塔等连接铰进行了拆分细化，建立了软刚臂系泊系统的三维多体动力学模型，构建了现场监测数据与多体模型广义坐标向量的关系表达式，对软刚臂系泊系统的水平系泊力和垂向系泊力进行了计算。进而利用现场冗余监测信息对模型计算结果进行验证。

1 软刚臂系泊系统多体动力学模型

1.1 软刚臂单点系泊系统的多体连接拓扑结构

软刚臂单点系泊系统主要包括系泊支架、系泊腿、系泊刚臂、和单点转塔4部分结构，其中系泊支架与船体固接。软刚臂系泊系统共有13个铰节点连接构成。其中系泊腿的上铰节点，连接系泊腿和系泊支架，由3个转轴沿不同方向旋转铰依次连接构成，释放系泊腿横摇、纵摇以及轴向转动的功能。系泊腿的下铰节点由2个旋转铰连接构成，释放系泊腿的横摇和纵摇旋转自由度。

图1为软刚臂系泊系统及其拓扑结构图。定义单点转塔作为B0号单体，与大地坐标系固连；滑环转盘为B1号单体；系泊刚臂旋转接头为B2号单体；系泊刚臂为B3号单体；左、右系泊腿分别为B4号单体和B5号单体；系泊支架为B6号单体。H1～H7为各单体的连接铰结构。表1给出了软刚臂系泊系统多体动力学模型各单体及各铰节点连接方式。

图1 软刚臂系泊系统拓扑结构Fig.1 Topological graph of soft yoke mooring system

表1 软刚臂系泊系统各单体和铰节点名称Table 1 Names of individual units and hinge nodes of SYMS

由于系泊腿的上部铰节点和下部铰节点尺寸远小于系泊腿的长度，在建模过程中，将它们分别模型化为球铰和万向节。

系泊刚臂与单点转塔的连接结构由系泊刚臂系泊刚臂旋转接头、1个旋转铰和位于单点转塔的滑环转盘构成，释放系泊刚臂绕单点转塔横摇、纵摇和艏摇的自由度。滑环转盘半径为2 m，系泊刚臂旋转接头长度为1.5 m，它们的尺寸相对单点转塔而言过大，如果忽略尺寸效应，将系泊刚臂与单点转塔的连接结构简化为一个球铰，会带来较大的建模计算误差。因此在建模过程中将系泊刚臂与单点转塔间的连接结构拆分细化为3个旋转铰和2个单体(系泊刚臂旋转接头和滑环转盘)。

1.2 软刚臂系泊系统多体动力学建模

由图1可以看出软刚臂系泊系统为典型的有根非树多体系统，在对其进行多体建模过程中选取左系泊腿上铰节点H7作为切断铰。

基于相对坐标方法，定义软刚臂系泊系统的广义坐标向量为:

Q=(q1,q2,q3,q41,q42,q51,q52,q61,q62,q63)

式中：q1为滑环转盘的转动角度；q2为系泊刚臂旋转接头绕滑环转盘的转动角度；q3为系泊刚臂旋转接头沿系泊刚臂轴线方向的转动转角度；(q41,q42)、(q51,q52)分别为左、右系泊腿下铰节点的转动角度；(q61,q62,q63)为右系泊腿上铰节点的转动角度。

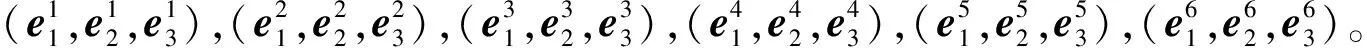
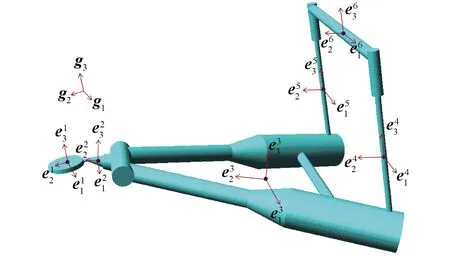
图2 各单体随体坐标系Fig.2 Satellite coordinate system of each monomer

各个单体的随体坐标系通过铰节点转换矩阵均能够用大地坐标系表示。各个铰节点由于铰的类型不同以及铰节点的转轴方向不同，各铰节点的转换矩阵也不同[12]。软刚臂系泊系统中各个铰节点的转换矩阵为Ai(i=1，2，…，6)，各单体的随体坐标系可通过大地坐标系和铰节点转换矩阵表示[13]：

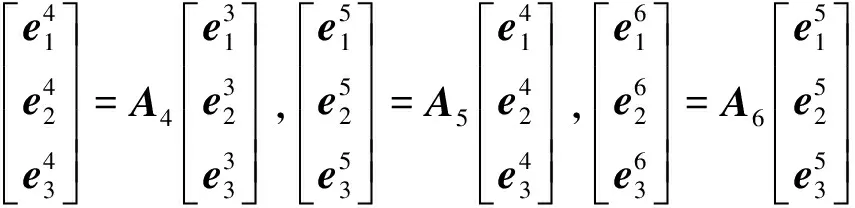
(1)

各铰节点的转轴矢量为：

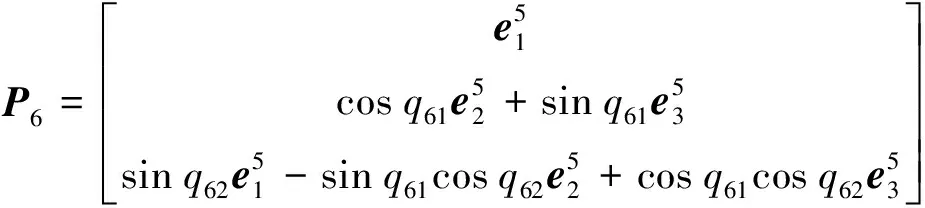
(2)

系泊系统各单体的质心位置和体铰矢量如图3所示，各单体质心位置表示为Oi(i=1，2，…，6)，物体i到物体j的体铰矢量表示为Cij(i=1，2，…，6,j=1，2，…，6)。各个单体的质心位置矢量为：

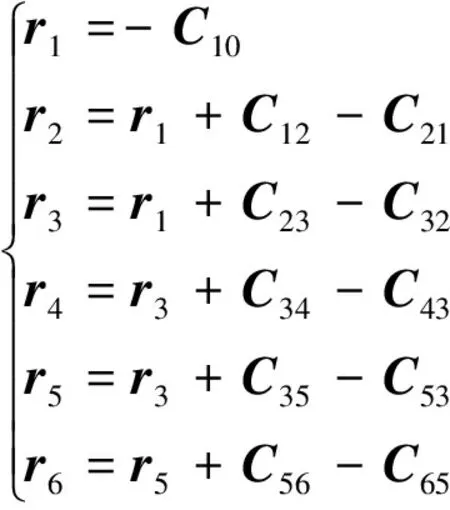
(3)

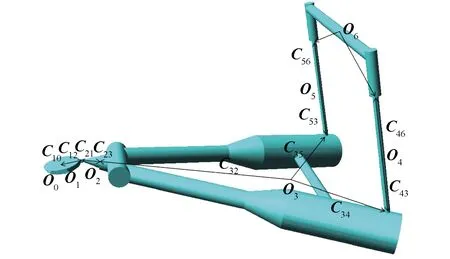
图3 软刚臂单点系泊系统多体动力学模型各单体质心及体铰矢量Fig.3 The center of mass and body hinge vector of each single body in multi-body dynamics model of SYMS

与切断铰H7相连接的系泊腿和系泊支架的相对位移为h7=r6+C64-r4-C46，切断铰为球铰，仅有旋转自由度，故相对位移为零。对表达式两边对时间求二次导数，可以得到切断铰的加速度约束方程：

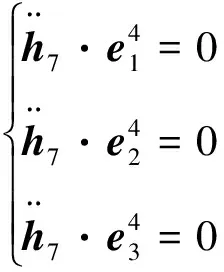
(4)

式(4)可以写成约束雅克比矩阵形式：

(5)

式中t7为广义速率引起的加速度。

由虚功率原理可以得到软刚臂系泊系统的多体动力学方程为：

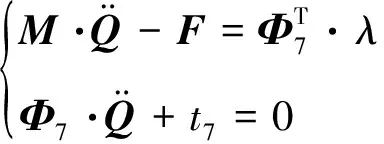
(6)

式中：M为18×18的软刚臂系泊系统广义质量矩阵；F为系泊系统广义力向量；Φ7为约束雅克比矩阵；λ为拉氏乘子列向量。根据拉氏乘子的力学意义；λ=[F61F62F63]T为左系泊腿上铰节点的约束反力。

2 基于现场监测数据的多体动力学模型验证分析

2.1 软刚臂系泊系统现场监测数据

在渤海某浮式生产储卸油装置建立了一套软刚臂原型监测系统：海洋环境监测子系统，监测风、浪、流环境荷载信息；浮体监测子系统，监控船体位置和六自由度运动信息；软刚臂姿态监测子系统，监控系泊刚臂和系泊腿的姿态信息[14]。

为了让软刚臂系泊系统的多体动力学模型适用于现场，首先建立多体动力学模型广义坐标向量与现场监测信息的关系。软刚臂系泊系统由7个铰节点构成，一共有13个自由度。由于其为闭环系统，对系泊腿上铰节点进行切断，得到其派生树系统具有10个独立的自由度。其中切断铰为球铰，具有3个位移约束方程，则软刚臂监测系统整体自由度为7[11]。建立软刚臂多体动力学模型广义坐标向量与现场监测信息之间的关系公式为：

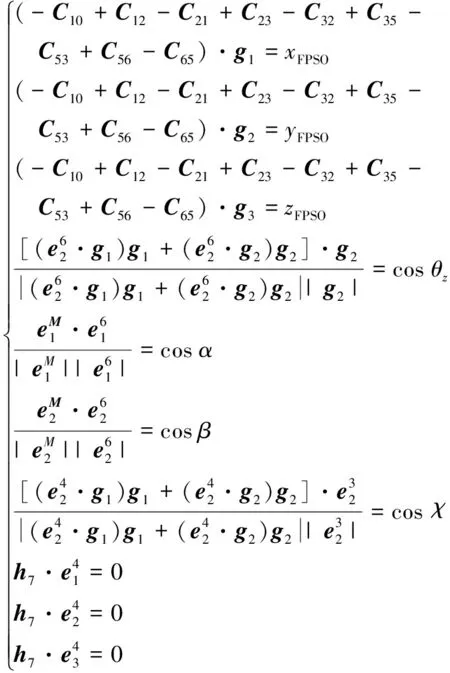
(7)

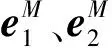
结合现场监测数据，对软刚臂系泊系统的运动行为进行分析。选取2016年2月13日13:30至14:00的船体六自由度实测数据和左系泊腿横摇值作为输入条件。由于系泊支架与船体固连，通过现场监测系统中对船体横荡、纵荡、垂荡、横摇、纵摇、艏摇六自由度的监测以及左系泊腿相对横摇(左系泊腿随体坐标轴与水平面夹角)的监测信息即可计算软刚臂系泊系统的广义坐标向量，即各个铰节点的转动角度。

对于切断铰H7的转动角度(q71,q72,q73)，可通过左系泊腿与系泊支架随体坐标系的基矢量关系求得：

(8)

2.2 软刚臂系泊系统多体动力学模型验证分析

软刚臂系泊系统原型监测系统同步监测了左系泊腿相对纵摇、右系泊腿相对横摇、右系泊腿相对纵摇、系泊刚臂相对横摇等信息，这些监测信息可以作为现场监测的冗余信息，与软刚臂系泊系统的多体动力学计算结果进行对比分析，验证模型的准确度。对比结果如图4所示。

结果对比可以看出，本文所建立的软刚臂多体动力学模型能够真实的反映软刚臂系泊系统在实际服役中的运动状态，准确还原了软刚臂系泊系统各个单体及各个铰的运动时程，验证了所建立多体动力学数值方法的正确性和可行性。

2.3 系泊回复力模拟结果

系泊回复力是评价系泊系统和船体安全性能的重要指标，基于软刚臂原型监测结果分析可知，软刚臂系泊系统失效主要发生在系泊腿上铰节点[15]，而系泊回复力主要是由上铰节点提供。因此对系泊力的实时仿真十分重要。目前常规的软刚臂系泊力计算方法多采用二维简化力学模型[11],如图5所示。

软刚臂系泊系统水平和垂向系泊力的二维计算公式为：

(9)

(10)

式中：L3为系泊刚臂长度；L5为系泊腿长度；φ1为系泊刚臂与水平面夹角；φ2为系泊腿与垂向的夹角；G1、G2、G3分别为系泊刚臂、系泊刚臂压载舱以及系泊腿的重力。将实测的φ1、φ2代入到上述方程中，即可实时求解软刚臂系泊系统的水平系泊力和垂向系泊力。

图4 软刚臂系泊系统模型计算结果与现场监测信息对比Fig.4 Comparison of calculation results of SYMS model with on-site monitoring information

将软刚臂系泊系统三维模型的系泊回复力计算结果与二维模型进行对比分析，如图6所示。其中实线为三维模型系泊回复力的时程曲线，虚线为依据于传统二维力学模型计算得到的铰节点合力结果。

从图7可以看出软刚臂系泊系统的三维动力学模型由于全面考虑了系泊结构的动力学效应以及横向运动的影响，对系泊力的计算结果要大于传统的二维模型。其中水平系泊力趋势一致，但幅值更大，某些时刻数值大了一倍左右。垂向系泊力由于考虑了垂体横向运动的影响，整体均值较二维模型大了200 kN左右。

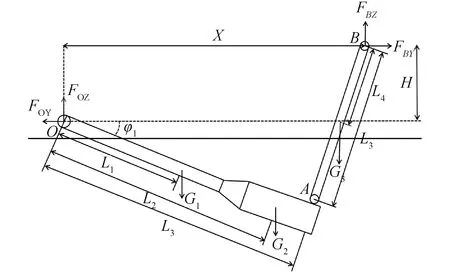
图5 软刚臂系泊系统二维力学模型Fig.5 Two-dimensional mechanical model of soft yoke mooring system

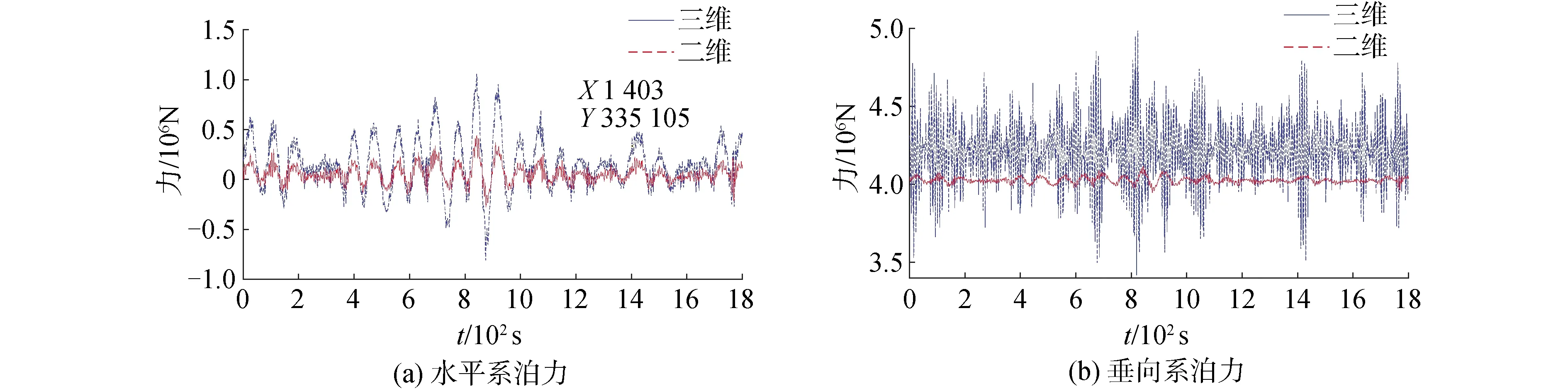
图6 系泊回复力时程图对比Fig.6 Comparison of mooring restoration force time history diagram

图7 系泊力频域分析对比Fig.7 Comparison of frequency domain analysis of mooring force

软刚臂系泊系统的三维动力学模型由于全面考虑了系泊结构的动力学效应以及横向运动的影响，对系泊力的计算结果要大于传统的二维模型。对系泊力频域分析，如图7所示，可以看出水平系泊力主要受低频运动的影响，垂向系泊力由于考虑了船体横向运动的影响，出现了剧烈的波频效应，这主要是受船体和系泊结构横摇的影响，因此波频运动也是影响软刚臂系泊系统结构设计的关键。

如图8所示，计算了软刚臂系泊系统水平系泊回复力对船体六自由度的相关系数，图9为垂向系泊力对各自由度的相关系数。对比结果可以看出水平系泊力与船体纵荡、横荡相关性较高，其次为船体的纵摇。而船的横荡、纵荡、艏摇为低频运动，垂荡、横摇、纵摇为波频运动。水平系泊力的能量主要集中在低频，因此，水平系泊力的低频能量主要受船体纵荡、横荡主导，而波频能量受纵摇主导。垂向系泊力与浮式生产储卸油装置的垂荡和纵摇的相关系数最高，其次为浮式生产储卸油装置的纵荡和横荡，而垂向系泊力是波频为主、低频为辅。其波频能量主要受垂荡、纵摇控制，而低频能量主要受纵荡影响。软刚臂系泊系统的横向运动直接影响系泊系统的水平系泊回复力，对在役软刚臂系泊系统系泊力分析需采用三维多体动力学计算，不应对横向运动进行简化处理。

图8 水平系泊力相关系数Fig.8 Horizontal mooring force correlation coefficient

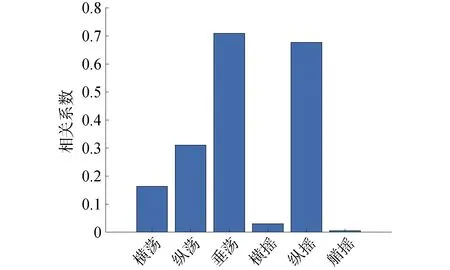
图9 垂直系泊力相关系数Fig.9 Vertical mooring force correlation coefficient

2.4 软刚臂各铰节点受力分析

软刚臂系泊系统在复杂的海洋环境中，铰节点受力复杂，而它们往往不能直接测量，因此基于现场监测数据，通过软刚臂系泊系统多体动力学模型对各个铰节点进行实时受力分析十分重要。通过将现场监测到的7个自由度信息代入到多体动力学模型中，计算出各个铰节点的受力时程如图10所示。

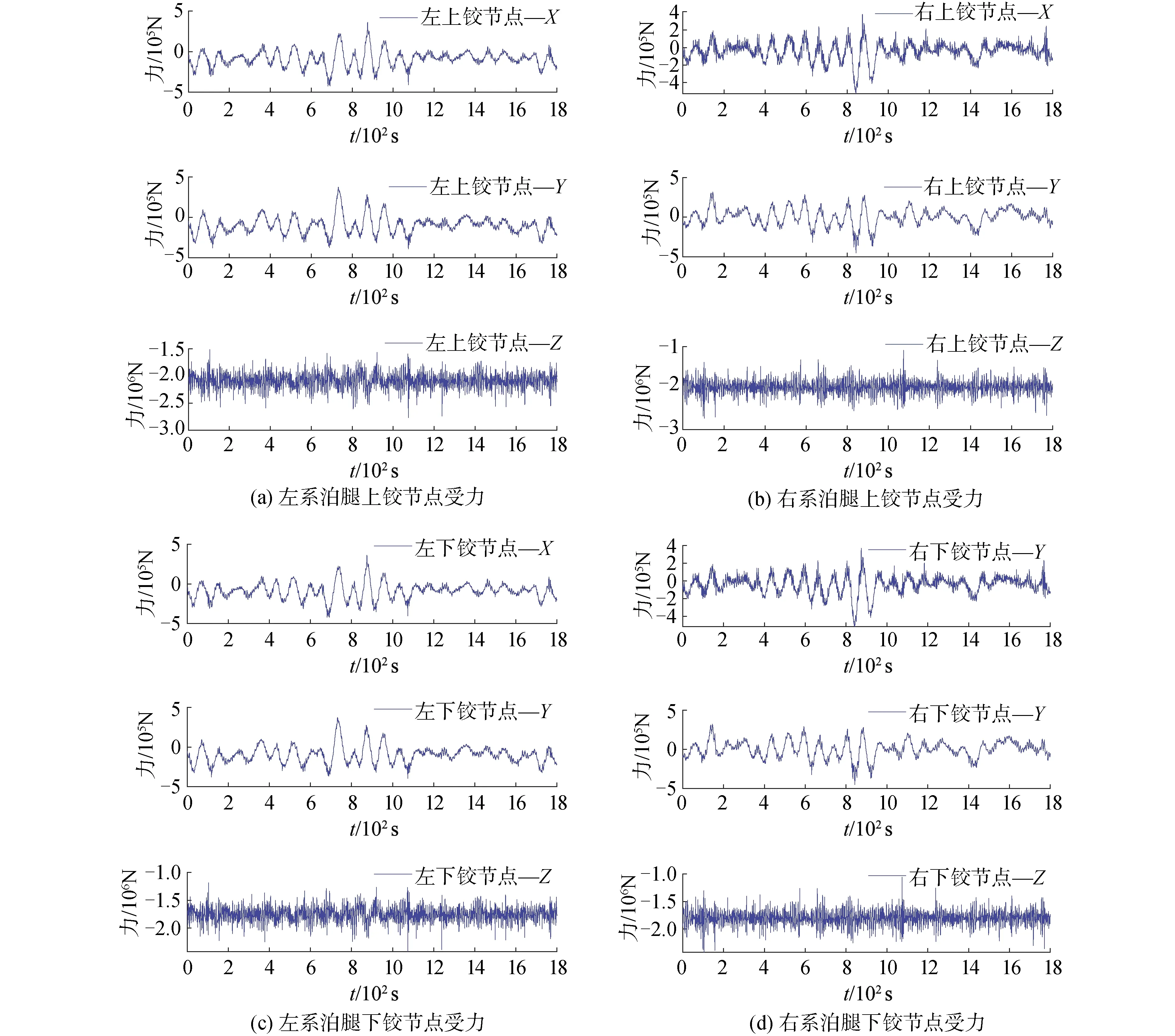
图10 软刚臂系泊系统铰节点受力时程图Fig.10 Time history diagram of force on hinge joints of soft

从图10中可以看出，左系泊腿和右系泊腿的铰节点在水平方向受力变化较为平缓，两者变化趋势一致，但幅值上稍有差异。系泊腿的上、下铰节点在竖直方向受力变化较水平方向较剧烈，其中右系泊腿竖直方向受力变化较左系泊腿更剧烈。说明在复杂的海洋环境作用下软刚臂系泊系统左、右系泊腿的铰节点受力并非完全对称一致。

3 结论

1)本文考虑了软刚臂系泊系统的铰结构大尺寸、自重大等结构特点，对系泊刚臂与单点转塔的连接铰进行了拆分细化，建立了软刚臂系泊系统的三维多体动力学模型。基于原型监测，构建现场监测数据与多体模型广义坐标向量的关系表达式，使模型能够适用于服役中的软刚臂系泊系统。对比现场监测的冗余信息，证明所建立的多体动力学模型能够真实全面地描述软刚臂系泊系统在服役过程中各铰节点和单体的运动状态。

2)将软刚臂系泊系统的系泊回复力计算结果，与传统的二维力学模型进行对比，由于考虑了船体和系泊结构的横向运动，三维多体动力学模型系泊力幅值明显大于二维模型的计算结果，其中水平系泊力某些时刻数值大了一倍左右，垂向系泊力整体均值较二维模型大了200 kN左右。并且垂向系泊力具有明显的波频效应，说明软刚臂系泊系统的系泊回复力受到低频运动和波频运动的耦合作用，在软刚臂系泊系统的设计阶段需要着重考虑。

3)基于现场监测数据，计算了软刚臂系泊系统各铰节点在真实海况下的受力状态。建立的软刚臂系泊系统多体动力学模型能够计算出系泊刚臂与单点转塔间具体连接结构的动力响应，且连接结构的受力时程能够为系泊刚臂的疲劳分析提供数据支持。