布拉格共振条件下的高阶谐波特性研究

张时斌， 宁德志， 陈丽芬， 张崇伟， 滕斌

(大连理工大学 海岸及近海工程国家重点实验室，辽宁 大连 116024)

在近海区域，人们常能发现周期性规则沙坝[1-4]。这些沙坝的坝高最高可达1.5 m，而间距从数米到数百米不等[5]。Davies[6]通过摄动方法研究波浪与周期性沙坝相互作用时，发现当入射波浪波长为沙坝波长的两倍时，连续沙坝产生的同相位弱反射波将在地形迎浪侧叠加形成强反射波，产生高度共振的自由表面运动，即布拉格共振现象。该现象被Heathershaw[7]的物理实验所证实。Davies等[6,8]的摄动方法在共振反射区，即当2k1/kb=1时(k1、kb分别为表面波和地形波的波数)，求得的反射系数超过1，与物理现实不符。Mei[5]利用多尺度摄动法解决了Davies的这一理论缺陷。Yu等[9]基于线性浅水方程研究发现不仅存在2k1/kb=1的共振态，更有2k1/kb=2, 3, 4等高阶共振模态的存在。Chamberlain等[10]及O′Hare等[11]通过数值计算，同样得到了2k1/kb=2的高阶结果，更是在双周期沙坝地形(沙坝波数分别为kb1和kb2，且kb2=2kb1)条件下发现了2k1/kb=3,4，5时的共振现象。Liu等[12]采用多极展开结合极坐标变换的方法得到的解析结果显示，斜向入射波条件下也存在高阶共振模态。Zhang等[13]发现由于传统缓坡方程忽略了高阶项，局限了其在陡坡地形条件下的应用。

波浪与水下结构物相互作用时，由于浅水作用而产生的高阶谐波[14-18]，有可能同时诱发以上多种布拉格共振模态。并且布拉格共振的发生可能会反过来改变高阶谐波的特性，从而对周期性结构物周围的波浪场造成不可忽略的影响。

鉴于布拉格共振和高阶谐波都具有重要的工程意义，并且目前缺少对这2种现象的联合研究，本文将在前人的研究结果基础上，利用时域高阶边界元方法，在布拉格共振条件下，进行高阶谐波的特性研究。

1 布拉格共振的数值计算方法

在笛卡尔直角坐标系下考虑波浪与水下正弦形周期性地形(沙坝)相互作用的问题。笛卡尔直角坐标系Oxz的z轴向上为正，x轴向右为正(与入射波浪传播方向同向)。设置静水面为z=0平面，平底上方静水深为h。水槽底部布置波幅为b，波长为λb的n周期(下文称n为沙坝相对长度)正弦形沙坝结构ζ(x)：

(1)

式中：x1表示沙坝结构的起点坐标；kb为正弦形沙坝结构的波数。

假定流体为无粘、不可压缩且运动无旋的理想流体，引入势流理论来描述水槽内的流体运动。在数值模型中，本文采用内嵌源造波技术产生入射波浪，并且在水槽两端分别布置长为Lb的数值阻尼层以消除来自出流边界的波浪反射及造波边界的波浪二次反射，因此数值模型的控制方程和初边值条件为：

(2)

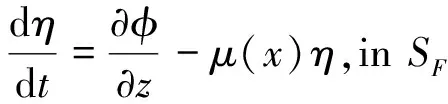
(3)

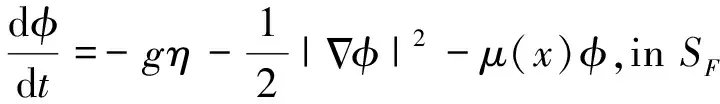
(4)

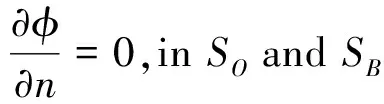
(5)

φ(x,z,t)=0，η(x,t)=0，t≤0

(6)

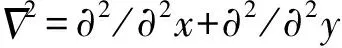
(7)

式中：ν为阻尼系数(=1)；Lb为阻尼层宽度，取为2倍波长；x01和x02分别为水槽两端阻尼层的起始位置。

Davies等[19]用水槽底部流体粒子水平位移幅度2Ab与地形波长λb的比值2Ab/λb(=2ga0k1/(λbω2cosh(k1h)，其中g为重力加速度，h为左端水平地形上的静水深，a0/k1/ω1分别为入射波的波幅/波数/角频率)来判别正弦波地形上流体的流动状态。当该参数～O(10-1)时，认为此时的流分离现象不严重，即流体粘性作用可以忽略。本文考虑的工况中，2Ab/λb最大为0.3～O(10-1)，因此，基于势流理论建立数值模型用以模拟研究波浪与周期性地形相互作用是合理的。同样，本文主要关注非破碎陡波在周期性地形上的传播变形；波浪破碎等会对波浪非线性、布拉格共振及高阶谐波特性产生一定的影响，但不在本文考虑的范围内，是本文下一步需要深入研究的内容。

本文采用高阶边界元方法求解上述方程(2)～(6)，具体求解方法详见文献[20]。数值计算中，通过收敛性分析，水槽自由表面网格尺寸和沙坝结构网格尺寸分别选为Δx=λ/30和Δx=λb/10，时间步长为Δt=T/60 (λ和T分别为表面波的波长和周期)。

2 布拉格共振对高阶谐波特性的影响

为了证明本文结果的准确性，将本文模型结果和已发表的实验结果及理论解进行对比。本文依照文献[7]及文献[19]的实验参数进行如下设置：沙坝波幅b=0.05 m，沙坝波幅与水深之比b/h=0.16，沙坝波长λb=1 m，沙坝相对长度n=10，入射波幅a0=0.01 m。

利用四点处(堤前1.6 m，间隔0.1波长布置)的波高信息进行入反射分离得到堤前的反射系数(具体的分离方法参见文献[21])，其随入射波数的变化规律见图1。可以发现，本文模型结果与理论解吻合良好，但在布拉格共振条件附近与实验结果相比，高估了共振反射系数。

图1 堤前反射系数随入射波数的变化Fig.1 Reflection coefficients as a function of the wavenumber

图2给出了布拉格共振条件下，反射系数的空间分布(沿水槽中线布置一系列浪高仪，同样利用四点法进行入反射波分离)。同样发现，在沙坝的迎浪侧，本文模型结果相对于实验结果高估了反射系数。反射系数的高估可能是实验结果受到来自造波板二次反射的影响，且这也可能是造成地形左端水平地形上反射系数沿程变化的原因。而在沙坝的背浪测，实验结果则可能受到水槽右侧消波区反射波(实验消波区未能吸收所有透射波)的影响而产生波动。

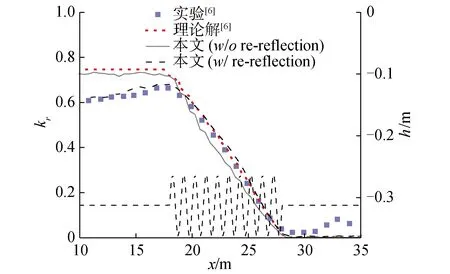
图2 布拉格共振下反射系数的空间变化Fig.2 The spatial distribution of the reflection coefficient under the Bragg resonant condition

将数值模型的源造波法转换为用速度势入口法进行造波(速度势同样根据二阶斯托克斯方法给定)，则此时行进波在遇到结构物(周期性地形)后产生的反射波会在入口(造波板)处产生二次反射。图1、2中也给出了考虑二次反射的计算结果(黑虚线)，可以发现，新的结果和实验结果十分吻合，由此证明了上述猜想以及本文数值模型模拟布拉格共振现象的可靠性。

2.1 沙坝波幅的影响

所建立/验证的模型现用于模拟研究沙坝地形参数对布拉格共振和高阶自由谐波特性的影响规律。

图3给出了3组不同沙坝波幅条件下，反射系数随入射波数的变化情况。图中虚线指示出布拉格共振的理论位置(2k1/kb=1)。可以发现反射系数在2k1/kb=1附近取得最大值，并且其峰值和带宽均随沙坝波幅增加而增加(峰值最大值为1)。另外，共振峰值频率相对于理论共振频率(2k1/kb=1)出现低频偏移现象，且偏移程度随波幅增加而增加。该趋势与Liu等[22]据摄动理论计算给出的低频偏移现象一致。另外在高阶布拉格共振条件2k1/kb=2处，发现随着沙坝波幅b/h增加，反射系数逐渐呈现局部峰值。这是由于该共振对应的波频较高，波浪能量主要分布于水体表层，只有当沙坝波幅较大时表面波才能受到沙坝地形调制从而产生共振。

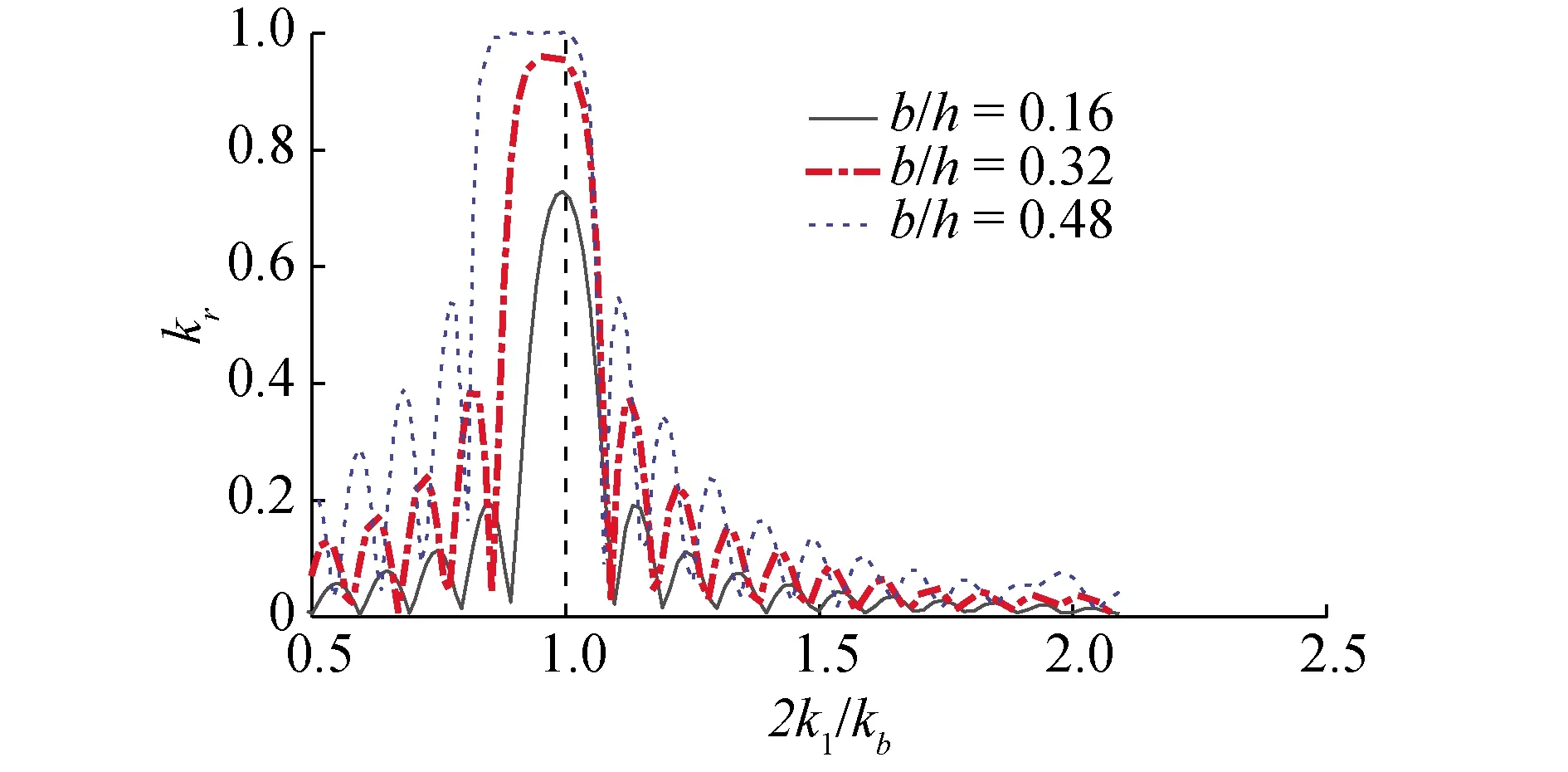
图3 不同沙坝波幅下反射系数随入射波数变化Fig.3 Reflection coefficients as a function of the wavenumber ratio for the three bar amplitudes

为了研究布拉格共振条件(2k1/kb=1)下，沙坝波幅对各阶谐波的影响，本文分别采用两点法[23]和四点法[21]分离沙坝背浪侧和迎浪侧的波浪组分。图4给出了沙坝迎/背浪侧的各阶波成分透反射系数随相对沙坝波幅b/h的变化。图例中上标r和t分别表示反射波和透射波；下标f和l分别表示自由波和锁定波；下标(1)和(2)分别表示一阶波浪和二阶波浪。

从图4可以看出，随着沙坝波幅的增加，基频波的共振反射系数逐渐增强并最终收敛至1。这一趋势与图3呈现的规律一致。在图4(b)和(c)中，二阶锁定波的透射系数和反射系数具有相反的变化趋势，即随着沙坝波幅增加，反射的二阶锁定波能量增加而透射的二阶锁定波能量减少。为了便于分析，图4(c)中用虚线标示了平底条件下测得的二阶锁定波无量纲波幅0.045(可视为入射波中的二阶锁定波成分的无量纲波幅)。可以发现，图中二阶锁定波的反射系数最终收敛至略高于此虚线处。因为二阶锁定波的波数为2k1，其同样满足图3中发现的高阶布拉格共振条件(2k1/kb=2)，所以可以推测布拉格共振条件下，二阶锁定波也将发生共振反射。而由于浅水效应诱导的基频波能量转移，其最终反射系数略高于入射二阶锁定波的波幅。此外二阶自由波透射系数和反射系数均随着沙坝波幅的增加而增加，前者在b/h=0.224时达到约0.05的饱和值，然后缓慢降低，后者则持续增加。

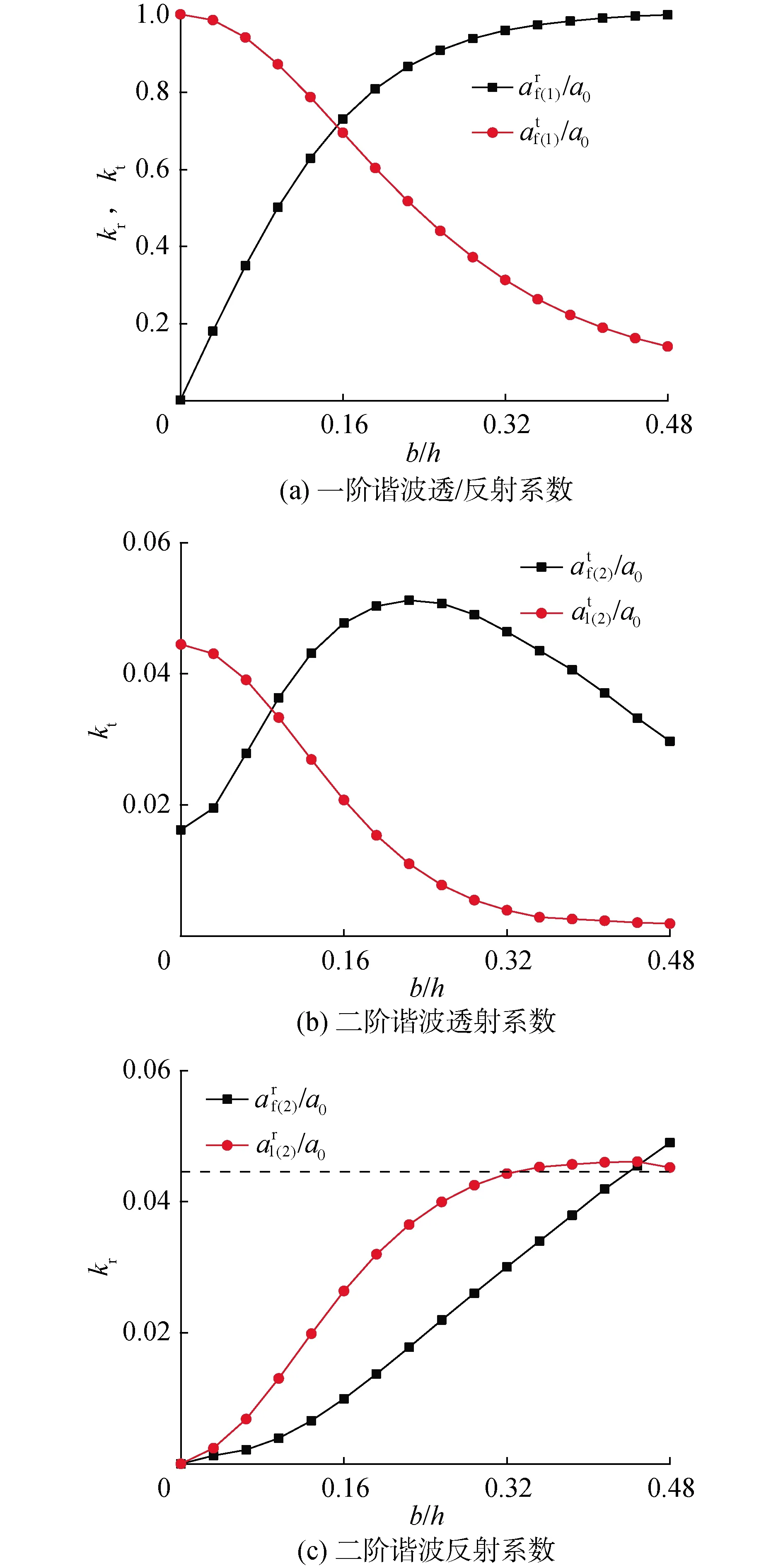
图4 布拉格共振条件下各阶谐波透/反射系数随相对沙坝波幅变化Fig.4 Variation of the reflection coefficient of the first two harmonics with the relative bar amplitude under the Bragg resonant condition

图5给出了布拉格共振条件(2k1/kb=1)下，不同沙坝波幅条件(b/h=0，0.16，0.32，0.48)下各阶谐波幅值的沿程变化(图中虚线指示沙坝左右边界)。水槽内每点的各阶谐波幅值是通过对空间内各点波面的时间历程进行快速傅里叶变换(FFT)得到。可以在图5(a)中清楚地发现在沙坝迎浪侧和上方，一阶谐波幅值出现了以1 m为空间周期的振荡。这是由一阶入射波和反射波线性叠加形成驻波所致(驻波理论节间距也为π/k1=1 m)。布拉格共振反射使沙坝上方的一阶透射波和反射波波幅沿程线性减小，进而导致一阶谐波幅值的振荡幅度沿沙坝长度方向线性减小并在沙坝末端收敛为一定值(即沙坝背浪侧的透射波波幅)。

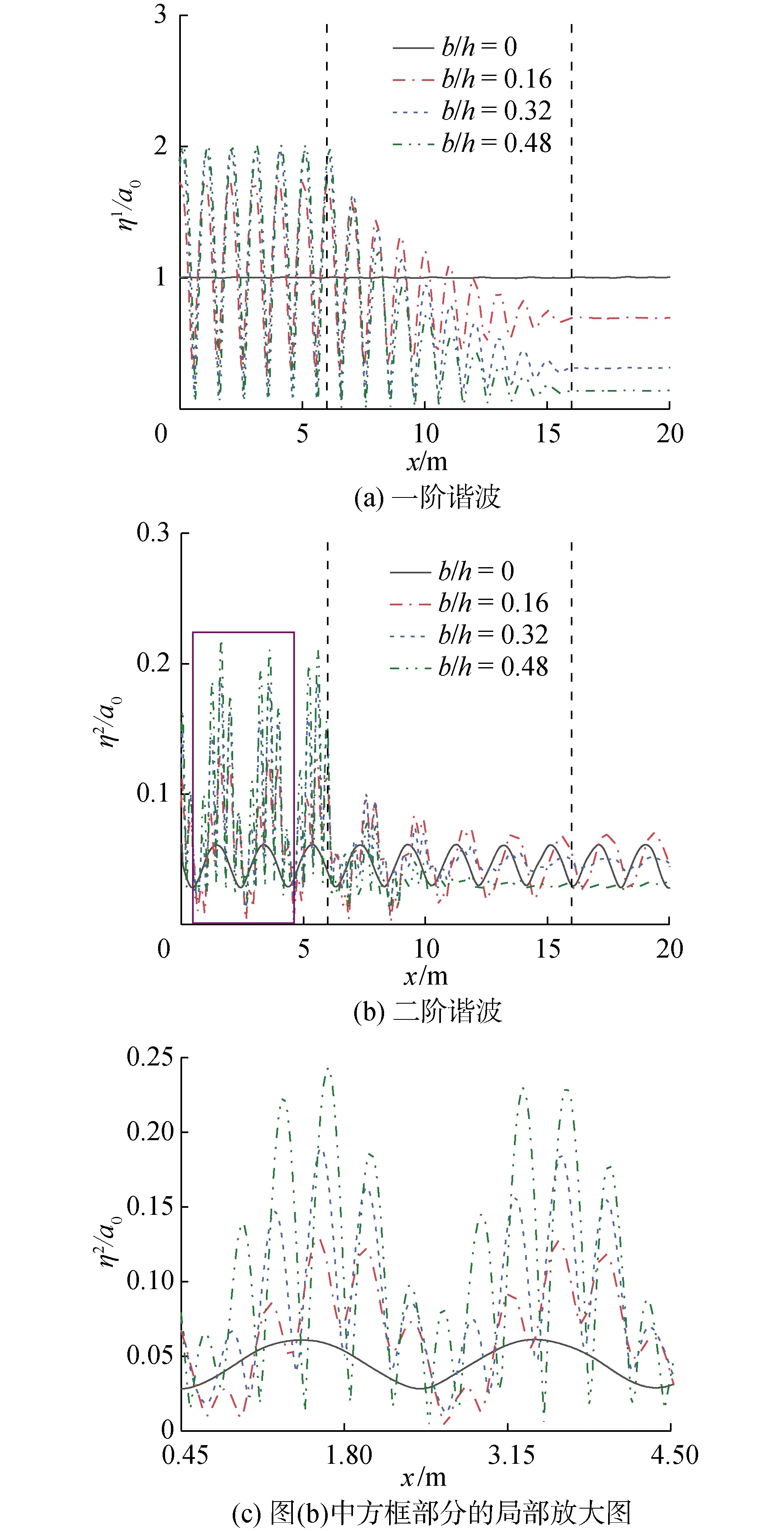
图5 布拉格共振条件下各阶谐波幅值沿程变化Fig.5 Spatial distribution of the wave amplitude of the first two harmonics under the Bragg resonant condition

有趣的是二阶谐波波幅的空间变化，首先在图5(a)中b/h=0的工况下，一阶谐波波幅沿水槽基本恒定。这说明在该工况下没有发生3波相互作用[24](3波相互作用将导致基频波和二阶波浪之间发生能量交换)。其次，可以在图5(b)中发现沙坝背浪侧的二阶谐波幅值出现了被称作“拍”的周期性振荡。譬如，在b/h=0.16时，实际测量所得的拍长为1.975 m，与理论拍长公式所得的结果1.939 m (=2π/(k2-2k1))较为接近。对比不同沙坝波幅条件下沙坝背浪侧的“拍”现象，可以发现沙坝波幅大小不改变拍长,但是会导致拍在空间上出现相位偏差。

在沙坝迎浪侧，二阶谐波幅值呈现出更复杂的空间变化(体现为在拍长1.975 m的主拍基础上出现数个寄生拍)，并且幅值变化的剧烈程度随沙坝波幅增加而增加。

对于“拍”的形成，Hansen等[25]给出了数学解释，即在平底条件下，水槽中二阶波面(忽略初始相位)通过三角函数变换可以写为：

(8)

式中第2项属于波群效应，其幅值随空间振荡但不随时间变化。波群成分的空间振荡周期(最大波幅值或最小波幅值的间距)，就是上文提到的拍长L，其满足公式(k2-2k1)L/2=π,即拍长L=2π/(k2-2k1)。

从上述推导中可以发现，“拍”是二阶锁定波和二阶自由波之间相位不匹配导致的空间波幅周期性变化，因此如果缺少其中一种波成分，二阶谐波的“拍”现象将会消失而变为一定值。例如b/h=0.48的工况下，在图4(b)可以发现沙坝背浪侧二阶锁定波波幅较小，导致在图5(b)中相应的幅值变化曲线近似于水平直线。

与式(8)类似，沙坝迎浪侧的二阶波面(忽略初始相位)通过三角函数变换，可以写为：

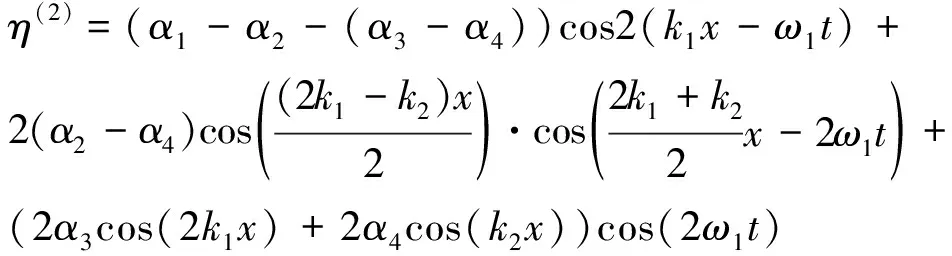
(9)

式(9)显示沙坝迎浪侧的波成分可以转变为行进波、具有波群特性的波和2个驻波的组合。前两者与式(8)相同，而后两者(即驻波)是新增加的成分。新驻波波幅的空间变化频率显著高于波群的波幅，这与图5(b)中的寄生拍的高频空间振荡现象一致，因此推断新驻波成分是寄生拍的成因。

当沙坝背浪侧某点的各阶波浪处于相同相位时，将形成较大波高的自由表面波浪，进而可能对附近的海岸结构物造成重要影响。因此，对于各阶波浪的相位进行研究分析是必要的，因为各阶锁定波处于锁相状态(同相位)，所以只需对各阶自由波相位展开研究。

图6显示布拉格共振条件(2k1/kb=1)下，沙坝背浪侧各阶自由波的初始相位随沙坝相对波幅b/h的变化。其中，初始相位是基于沙坝背浪侧G6(堤后1.6波长处)和G7(G6后0.1波长处)号探针处的波面时间历程，利用两点法得到。可以发现，自由波相位随着沙坝波幅增加而线性增加。通过线性拟合可以得到一、二、三阶自由波的初始相位变化斜率分别为1.65、3.60、4.85。其中，后两者分别约为前者的2倍和3倍。利用线性拟合直线，可以预测不同潜堤波幅条件下布拉格共振时堤后各阶自由波的初始相位，进一步可以确定堤后波高最大处，即各阶波浪同相位点。

图6 布拉格共振条件下沙坝背浪侧各阶自由波初始相位随地形幅值的变化Fig.6 Variation of the initial phases of the free waves behind the submerged dikes with the bar amplitude under the Bragg resonant condition

2.2 沙坝长度的影响

为了增强高阶谐波的能量，下文结果集中于相对沙坝波幅为0.32的算例。图7给出了沙坝相对长度n分别为2、5、10时，基频波反射系数随入射波数变化的结果。可以发现，随着n变大，布拉格共振峰值和次峰数量增加，而共振带宽减小。

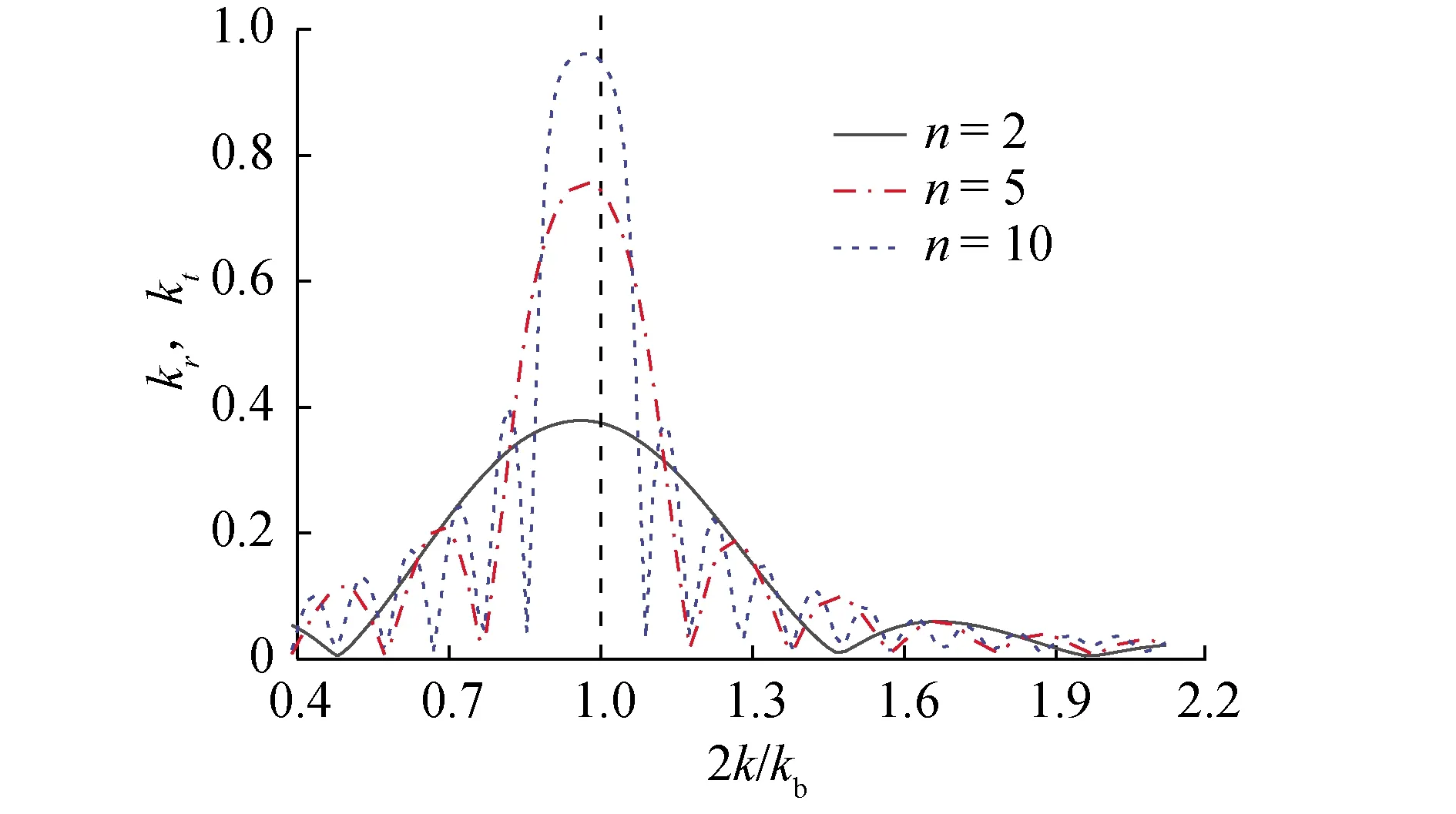
图7 基频波反射系数随入射波数变化Fig.7 Reflection coefficients of the fundamental wave as a function of the wavenumber ratio

图8给出了实测共振峰值频率ωp随沙坝相对长度n的变化。可以发现随着n增大，共振峰值频率向着高频方向偏移，并且收敛于ωp=4.72附近。这一趋势与Wen等[26]得到的规律一致。根据布拉格共振的物理机制，即相邻沙坝产生同相位的反射波，则布拉格共振的准确数学条件可以表达为：

(10)

式中第1/2项表示入/反射波在单位波长沙坝上传播的相位变化;k1(x)与入射波频ω1之间满足线性色散关系ω12=gk1(x)tanhk1(x)[h-ζ(x)]，其中ζ(x)的表达式见式(1)。

图8 布拉格共振峰值频率随沙坝相对长度的变化Fig.8 Variation of the Bragg resonant frequency with the relative bar length

式(10)中取m=1时，即为布拉格共振条件(2k1/kb=1)。经计算，相应的理论共振频率为4.75 rad/s(通过该方法无法考虑沙坝长度的影响，其可被视为沙坝无穷长工况的结果)。该值相比未考虑水底波动地形得到的理论共振值[22]4.82 rad/s，更接近于图8中共振峰值频率的近似收敛值(ωp=4.72)。前者相对误差较于后者减小1.5%，即仅为0.6%。

经过分析，式(10)与数值结果不同的原因有2点：1)图8中获得的收敛频率并非为精确的无穷长地形条件下的共振频率(后者略大于前者)；2)因为波浪无法随着水深变化瞬时改变其波数，而上述推导中默认了波数的瞬变假设。该结果虽然依旧存在误差，但是相对于原理论共振频率[22]，一定程度提高了长沙坝工况下共振峰值频率的预测准确度。

(11)

式(10)可以改写为：

(12)

接着在前文布置的基础上，研究布拉格共振条件(2k1/kb=1)下，沙坝相对长度n对各阶谐波的影响。图9分别给出了基频波和二阶谐波的透反射系数随相对长度n的变化。

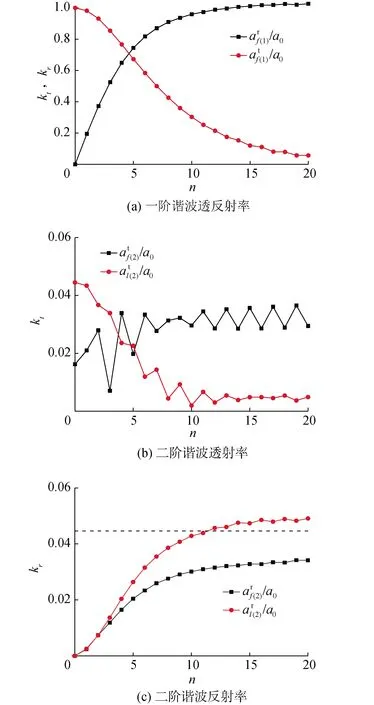
图9 布拉格共振条件下各阶谐波透/反射系数随沙坝相对长度变化Fig.9 Variation of the reflection and transmission coefficients of the first two harmonics with the relative length under the Bragg resonant condition

可以发现，图9中基频波与二阶锁定波透反射系数的整体趋势与随沙坝波幅变化的相应结果(图8)基本一致，这意味着沙坝相对长度n和沙坝相对波幅b/h对这两种波成分在布拉格共振条件下的影响类似(此处不再赘述)；二阶自由波透反射系数均随n增大而增大，并最终各自稳定于一定值附近振荡。值得注意的是随n变化的透反射率振荡现象在多个成分波浪中出现，其中二阶透射自由波尤为显著，这可能与图10(b)中的二阶自由谐波初始相位震荡现象有关。

图10给出了布拉格共振条件(2k1/kb=1)下堤后各阶自由波初始相位随沙坝相对长度n的变化。可以发现二阶自由波初始相位φ2以约为π的幅值，整体呈线性缓慢减小的趋势。该相位的振荡变化可能与图9中二阶谐波透射系数的振荡有关。此外基频波初始相位φ1初始线性增长；当沙坝长度继续增加，φ1出现小幅振荡并且增长率变缓。

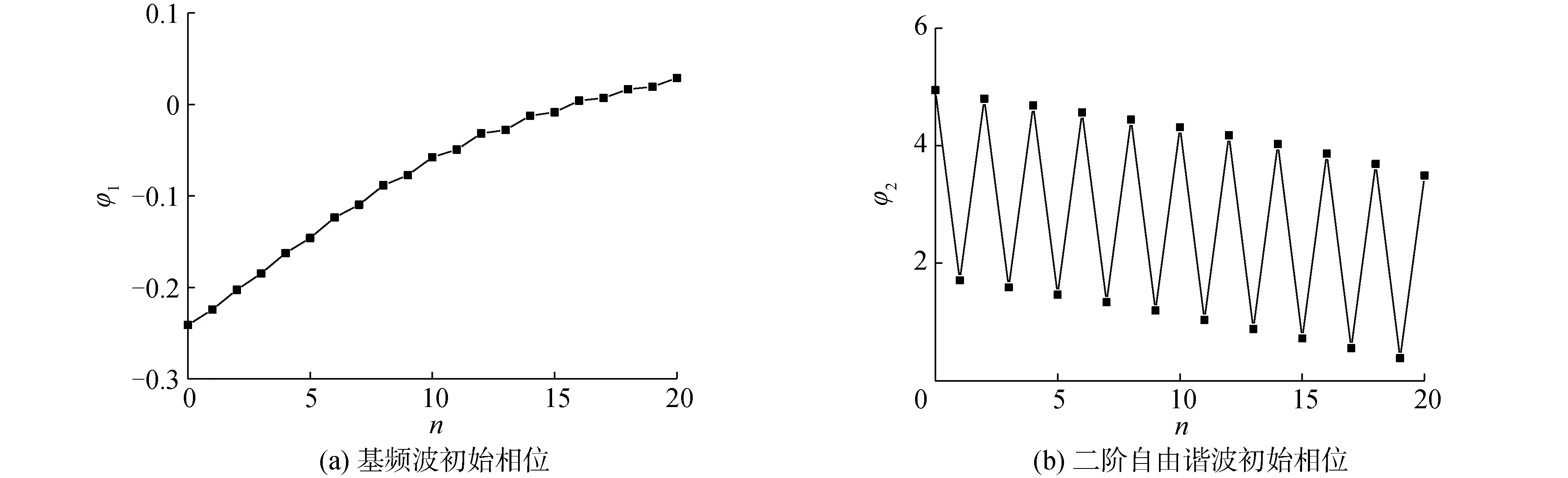
图10 布拉格共振条件下沙坝背浪侧各阶自由波的初始相位随地形长度的变化Fig.10 Variation of the initial phases of the free waves behind the submerged dikes with the bar length under the Bragg resonant condition

3 结论

1)随着沙坝波幅增加，布拉格共振峰值频率向低频偏移，共振带宽变宽，共振反射系数增加并收敛至1。

2)随着沙坝长度增加，布拉格共振峰值频率向高频偏移，共振带宽变窄，共振反射系数增加并收敛至1。

3)在布拉格共振条件下，二阶锁定波发生共振反射，并且反射系数随着沙坝波幅或沙坝长度而增加并最终收敛于入射二阶锁定波无量纲波幅附近。

4)随着沙坝波幅增加，二阶自由波透射系数先增大达到约0.05的饱和值，然后缓慢减小。二阶自由波反射系数则持续增大。

5)随着沙坝长度增加，二阶自由波透反射系数均增大，并最终各自稳定于一定值附近振荡。

6)布拉格共振条件下，在沙坝背浪侧的二阶谐波波幅会呈现“拍”的现象，而在沙坝的迎浪侧，除了“拍”以外，还存在附着于“拍”上的“寄生拍”，增加了极端大波出现的概率。