浅海粗糙海面影响下的声场水平纵向相关性
姚美娟, 鹿力成, 孙炳文, 马力, 郭圣明
(1.中国科学院 声学研究所, 北京 100190; 2.中国科学院 水声环境特性重点实验室, 北京 100190)
海洋声场空间相关特性是现代水声学中的重要研究内容,对阵处理增益具有重要的影响。随着大尺度水平阵和低频声波的广泛应用,浅海声场空间相关特性研究的实际应用价值越来越高[1],因此,开展不同水声环境下的声场空间相关特性研究具有重要意义。目前国内学者们开展了浅海斜坡海底、声速起伏环境等因素对声场相关特性的影响研究[2-6],给出了相应环境下的声场空间相关特性规律;国外学者较早就关注了声场空间相关特性,包括随机不均匀介质对声场相关特性的影响和多途通道中的声场空间相关性[7-9]等。
海面作为海洋波导的上界面,对海洋波导中的声传播有着重要的影响。理想情况下,认为海面是平整的,平整的海面对入射声波有着良好的反射特性。但在实际情况中,由于海面风浪的影响,海面经常是起伏的,起伏的海面对入射声波既有反射作用又有散射作用[10-13]。粗糙海面对声传播有着重要的影响:一方面,由于海面反射损失造成声能量的损失,进而引起接收阵信噪比的降低;另一方面,起伏的海面会引起声场能量的重新分布,进而对海洋声场空间相关特性产生影响。这两者共同影响着接收阵的阵增益,是后续阵处理工作的重要影响因素。目前对粗糙海面影响下声场的研究多集中在声传播损失上[14-15],因此,亟需开展浅海粗糙海面下的海洋声场相关特性研究。
本文将结合简正波声场模型,考虑风浪引起的粗糙海面因素,分析浅海海面风浪对声场水平纵向相关性的影响。并进一步通过简正波理论和简正波声场模型给出理论数值解释。
1 考虑粗糙海面影响的声场水平纵向相关性预报模型
1.1 粗糙海面的反射系数计算
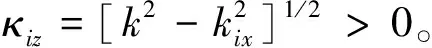
令
v=ki-ks=(vx,-vz),vx=kix-ksx,
vz=κiz+ksz,kβ1+i=[k2-(K1+kix)2]1/2
并且有
Im[β1+i]>0,kβs-1=[k2-(ksx-K1)2]。
最终可以得到小斜率近似下的反射系数为:
(1)
式中:kix≡ksx=kcosθi;κiz≡|ksz|=ksinθi;vz=2ksinθi;χ=vzh;g(K1)=kβi+1+kβs-1-vz;W(K1)为海面波浪谱的表面粗糙度幅度谱,它是粗糙面相关函数的傅里叶变换。目前已有多种形式的海面波浪谱,例如高斯谱、PM谱、NP谱和JONSWAP谱等。本文将采用国际上最为常用的PM谱[16]。
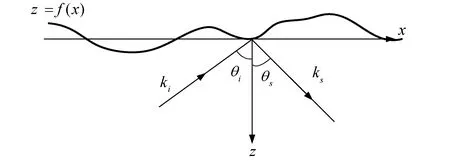
图1 一维粗糙海面散射示意Fig.1 Scattering sketch map for one-dimensional rough sea surface
对于PM谱,粗糙度幅度谱为:
(2)
将W(K1)代入式(1)可以计算SSA理论下的粗糙海面反射系数。
将计算得到的海面反射系数通过TRC(top reflection coefficient)文件[11]输入到Krakenc声传播模型中,可以计算考虑粗糙海面因素的声场。虽然将平均海面反射系数作为海面边界条件的声压场求解方法不能反应声压场的统计特性,但本文重在分析具有一定粗糙度的粗糙海面对声场水平纵向相关性的影响,暂时不关注随机波动海面下的声压场的统计特性。例如,朴胜春等[17]将海面相干反射系数引入到声传播模型中,基于简正波理论分析了波浪起伏对噪声场空间特性的影响。实际上,Krakenc声场模型的env输入文件中的粗糙度参数sigma,也是基于基尔霍夫理论转化为海面相干反射系数进而参与声场计算的,文献[14]对此也进行了分析。因此,将平均海面反射系数作为海面边界条件的声压场求解方法以及基于此进行的声场水平纵向相关性计算分析是合理的。
1.2 声场的水平纵向相关性
在同一接收深度z、不同接收距离(距离r和距离r+Δr)处2个接收点的声场相似程度可用声场的水平纵向相关性表征,声场的水平纵向相关性实际上就是2个水听器同时接收到的信号之间的归一化互相关系数,其计算公式为:
(3)
式中:pr(t)和pr+Δr(t)分别表示在距离r和距离r+Δr处接收到的声信号声压时域波形;τ为时延;Δr为水平纵向间隔,并且Δr≪r,频域的水平纵向相关系数表达式可由式(3)进行傅里叶变换求得:
(4)
式中:pr(ω)和pr+Δr(ω)分别表示在距离r和距离r+Δr处接收到的声信号声压频谱;ω表示角频率;ω0和Δω为信号的中心角频率和带宽。
由粗糙海面下的声场模型计算得到浅海粗糙海面影响下的频域声场,再根据式(4)可计算得到声场的水平纵向相关系数。
2 不同风速下的声场水平纵向相关性
图2为仿真计算的水声环境示意图,海深为100 m,水中声速剖面为1 510 m/s等声速剖面,海底为平坦海底,海底声速为1 587 m/s,海底密度为1.8 g/cm3,海底衰减为0.3 dB/λ。图3为数值仿真得到的声源深度SD和接收深度RD均为10 m时的平滑海面与粗糙海面下的宽带非相干传播损失对比图,频率选取200~300 Hz,频率间隔为10 Hz。从图中可以看到,在同一距离上,粗糙海面下的传播损失比平滑海面下的传播损失大;这将导致粗糙海面下的接收阵的信噪比降低,这个因素会引起阵增益降低。同时,粗糙海面对声波具有反射和散射作用,会引起声能量的重新分布,这将引起声场的空间相关性的改变,进而对阵增益产生另外的影响,本文从这个角度分析粗糙海面对声场空间相关性的影响。另外,由于本文重在探究粗糙海面引起的声信号能量的重新分布,以及这种重新分布下的声场空间相关性的改变,因此,没有考虑不同海面风速下由于海面反射损失引起的信噪比变化。
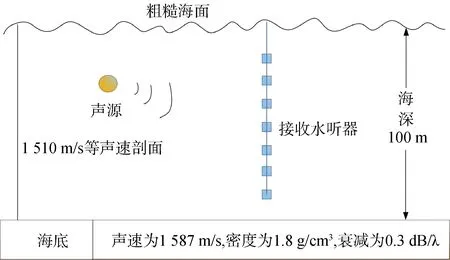
图2 数值仿真水声环境示意Fig.2 The acoustic environment for the simulation
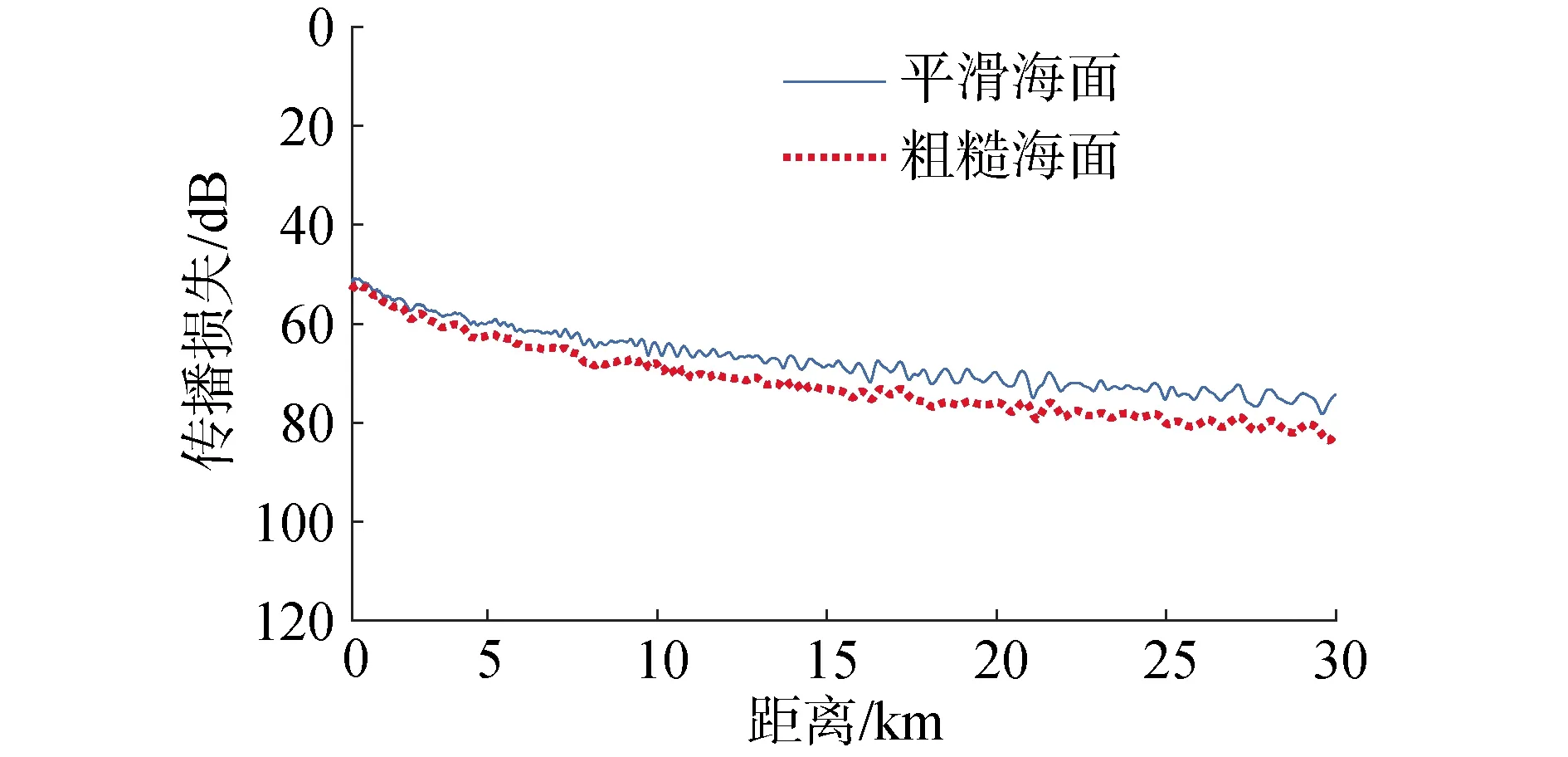
图3 粗糙海面引起声能量的损失示意Fig.3 The comparison of the transmission loss with rough surface and that with smooth surface
通过1.2节中介绍的方法仿真计算不同海面风速(风速分别为5、10、15、20 m/s)下的声场水平纵向相关性,水声环境同上,频率选取200~300 Hz,频率间隔为2 Hz。图4各子图分别是参考阵元的接收距离R为10 km时不同声源深度(source depth,SD)、不同接收深度(receiver depth,RD)上不同海面风速下的声场水平纵向相关性计算结果。图5各子图分别是参考阵元的接收距离R为20 km时不同声源深度SD、不同接收深度RD上不同海面风速下的声场水平纵向相关性计算结果。水平纵向间隔范围为500 m。
观察图4的每一个子图,很明显的可以看到,在给定的水平纵向间隔范围上,同一声源深度、同一接收深度、同一接收距离上的声场水平纵向相关性曲线在风速为0 m/s时和风速为5 m/s时是几乎重合的;而比较风速为5、10、15、20 m/s时的声场水平纵向相关性曲线,很明显的可以看到,在同一水平纵向间隔、同一声源深度、同一接收深度、同一接收距离上的声场水平纵向相关性是随着风速的增加而有所提升的。对比图4与图5其不同点在于图5中参考阵元的水平距离较远;对比图4与图5中的声场水平纵向相关性曲线,发现同一水平纵向间隔、同一声源深度、同一接收深度、同一风速条件下,图5中的声场水平纵向相关性优于图4中的声场水平纵向相关性。另外观察图4和图5中,在低风速时,水平纵向相关性曲线在水平间隔350 m处出现极小值,这其实是水平纵向相关曲线的振荡现象;而在高风速时则没有出现极小值,水平纵向相关曲线振荡现象减弱。
3 理论数值分析
为了解释第2节中的结果,在同样的水声环境下,从简正波理论出发对声场进行分析。以下是频率为250 Hz时以小斜率近似方法计算的不同风速下PM谱海面的相干反射系数的模。
通过图6可见,同一掠射角下,随着风速的增加,相干反射系数的模变小,反射损失变大;同一风速下,随着掠射角的增加,相干反射系数的模也变小,反射损失变大。低号简正波对应小掠射角,高号简正波对应大掠射角。换言之,在与海面发生碰撞时:对于同一号简正波,高风速下比低风速下衰减快;同一风速下,高号简正波比低号简正波衰减快。
下面将对频率为250 Hz时不同海面风速下的声场进行对比分析。根据简正波声场理论,可以将水平均匀环境中的声场写成各个简正模式叠加的形式:
(5)

图4 不同声源深度和接收深度上不同海面风速下的声场水平纵向相关性(R=10 km)Fig.4 Acoustic longitudinal horizontal correlation with different wind speeds (R=10 km)
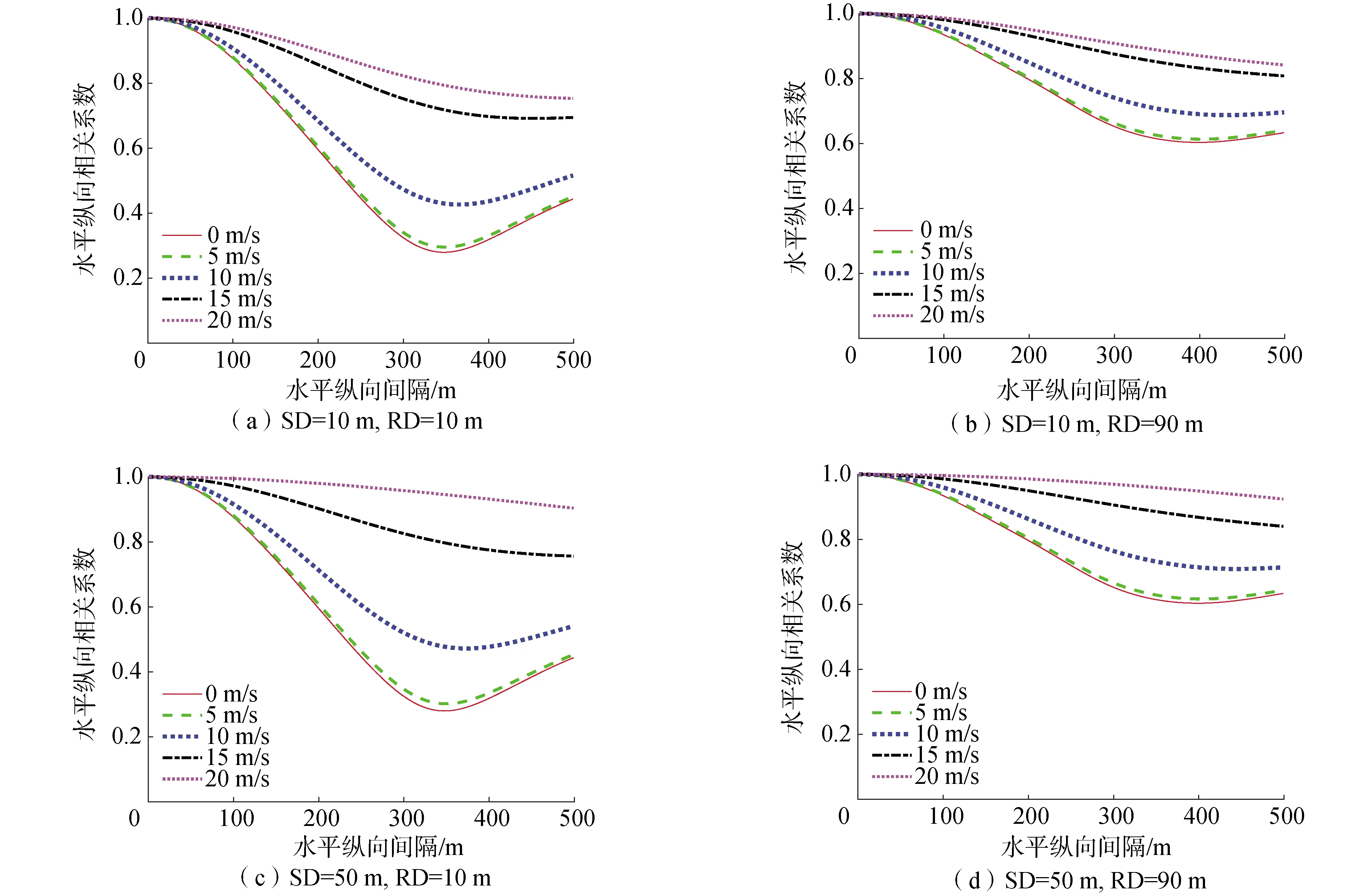
图5 不同声源深度和接收深度上不同海面风速下的声场水平纵向相关性(R=20 km)Fig.5 Acoustic longitudinal horizontal correlation with different wind speeds (R=20 km)
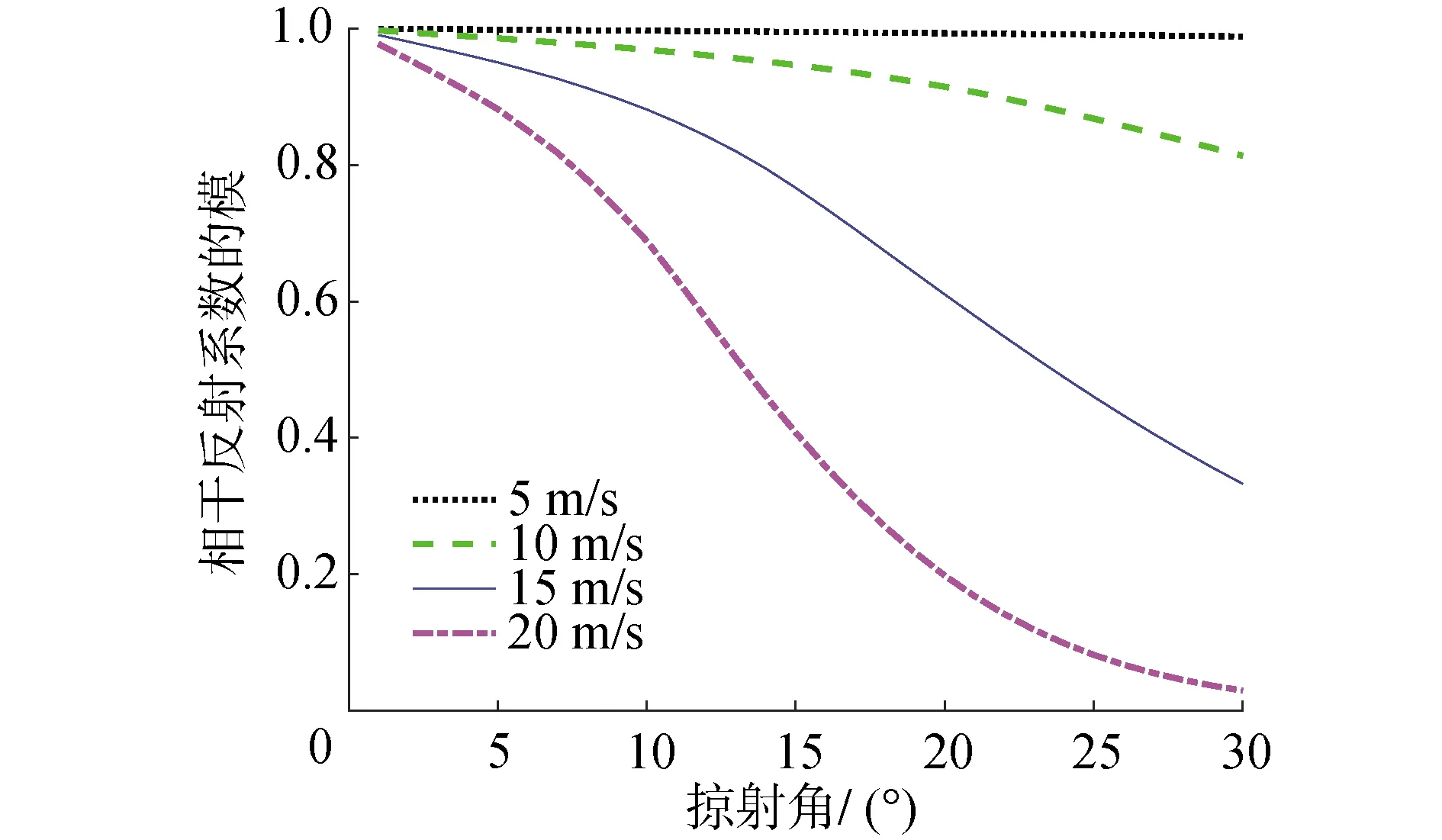
图6 不同风速下PM谱海面的相干反射系数的模Fig.6 The modulus of the coherent reflection coefficient of the sea surface of PM spectrum with different wind speeds
根据式(5),不同距离上声场中第l号简正波的幅值为:
(6)
为了对比方便,可以将各号简正波的幅值做归一化处理,即将每一号简正波幅值的模的平方除以各号简正波的幅值的模的平方和可以保证归一化处理之后的各号简正波的幅值的模的平方和为1:
(7)
图7给出参考阵元的接收距离R为10 km时不同海面风速下、不同声源深度(SD)、不同接收深度(RD)上的由Krakenc声场模型计算的各号简正波的归一化幅值的对比。图8给出参考阵元的接收距离R为20 km时不同海面风速下、不同声源深度(SD)、不同接收深度(RD)上的由Krakenc声场模型计算的各号简正波的归一化幅值的对比。
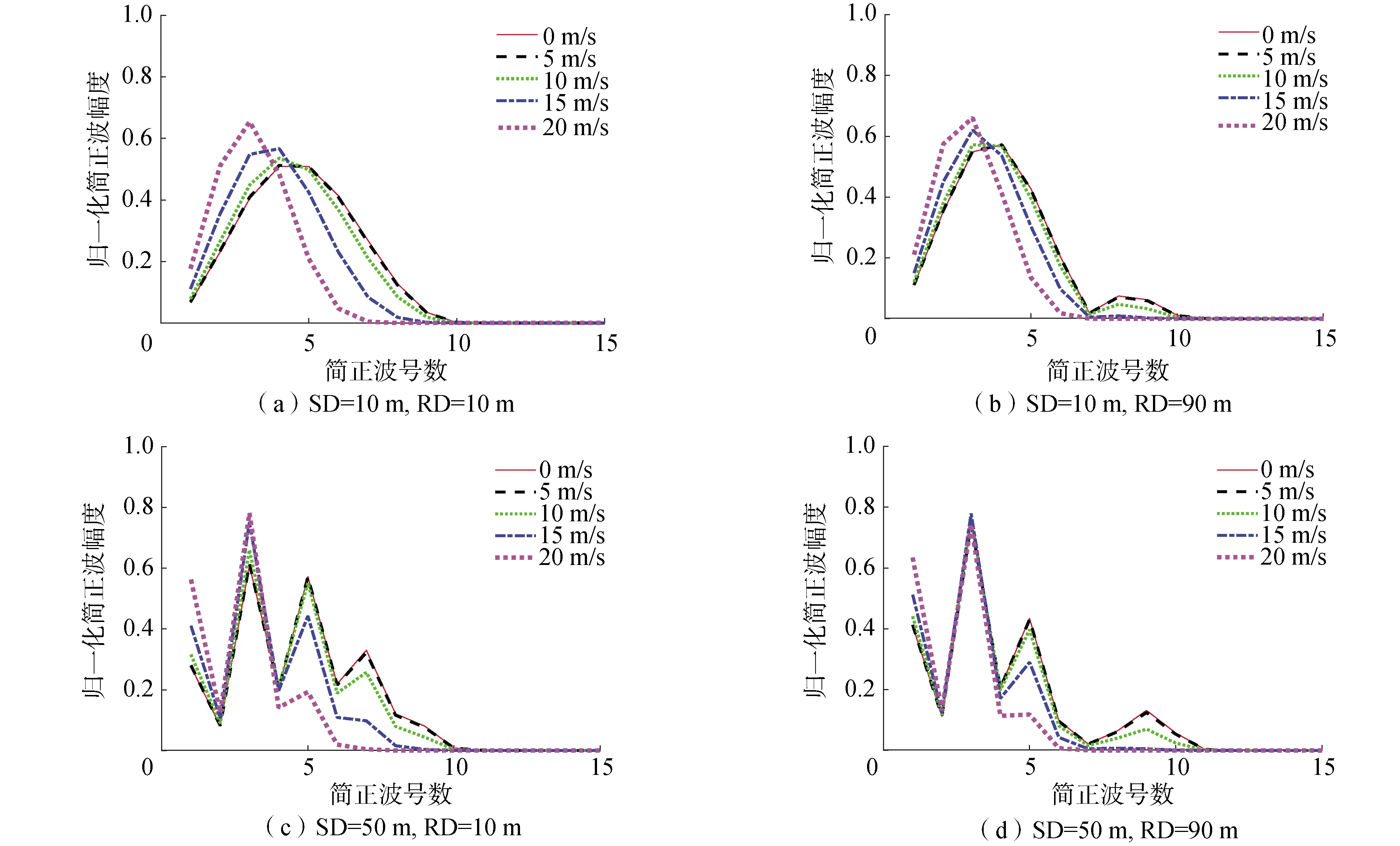
图7 不同海面风速下声场中各号简正波的归一化幅值的对比(R=10 km)Fig.7 Comparison of the normalization amplitude of each normal mode with different wind speeds (R=10 km)
观察图7和图8,风速为0和风速为5 m/s时的曲线几乎重合,可以由图6来解释:图6中风速为5 m/s时的海面相干反射系数的绝对值接近为1,对声场的影响较小。而随着风速的继续增加,各号简正波系数发生了明显的改变。在同一接收深度和接收距离上,随着风速的增加,声场的能量集中到更少的简正波号数中,并且集中到较低号的简正波号数中。以图7(a)、(b)和图8(a)、(b)为例进行分析,表1是对图7(a)、(b)中归一化幅值高于0.05的简正波号数的统计,此处暂且定义归一化幅值高于0.05的简正波为声场中的有效简正波;表2是对图8(a)、(b)中归一化幅值高于0.05的简正波号数的统计。从表1中可以看到:将表格作纵向对比,随着风速的增加,声场中的有效简正波号数减少。根据文献[4]中所述,简正波干涉会引起声场的水平纵向相关下降;文献[18]指出了声场水平纵向相关的振荡结构是由简正波干涉所致。而在表1中,随着风速的增加,导致有效简正波号数的减少以及相互之间干涉的减弱,因此,声场的水平纵向相关性会提高,并且水平纵向相关性曲线的震荡减弱。另外,比较表1和表2,在相同的声源深度和接收深度以及同一风速下,表2中的有效简正波号数少于表1中的有效简正波号数,这是由于随着水平距离的增加,高号简正波衰减更快,导致较远距离上(表2)的声场中有效简正波号数减少以及相互之间干涉的减弱。以上就是第2节中所述现象的原因。
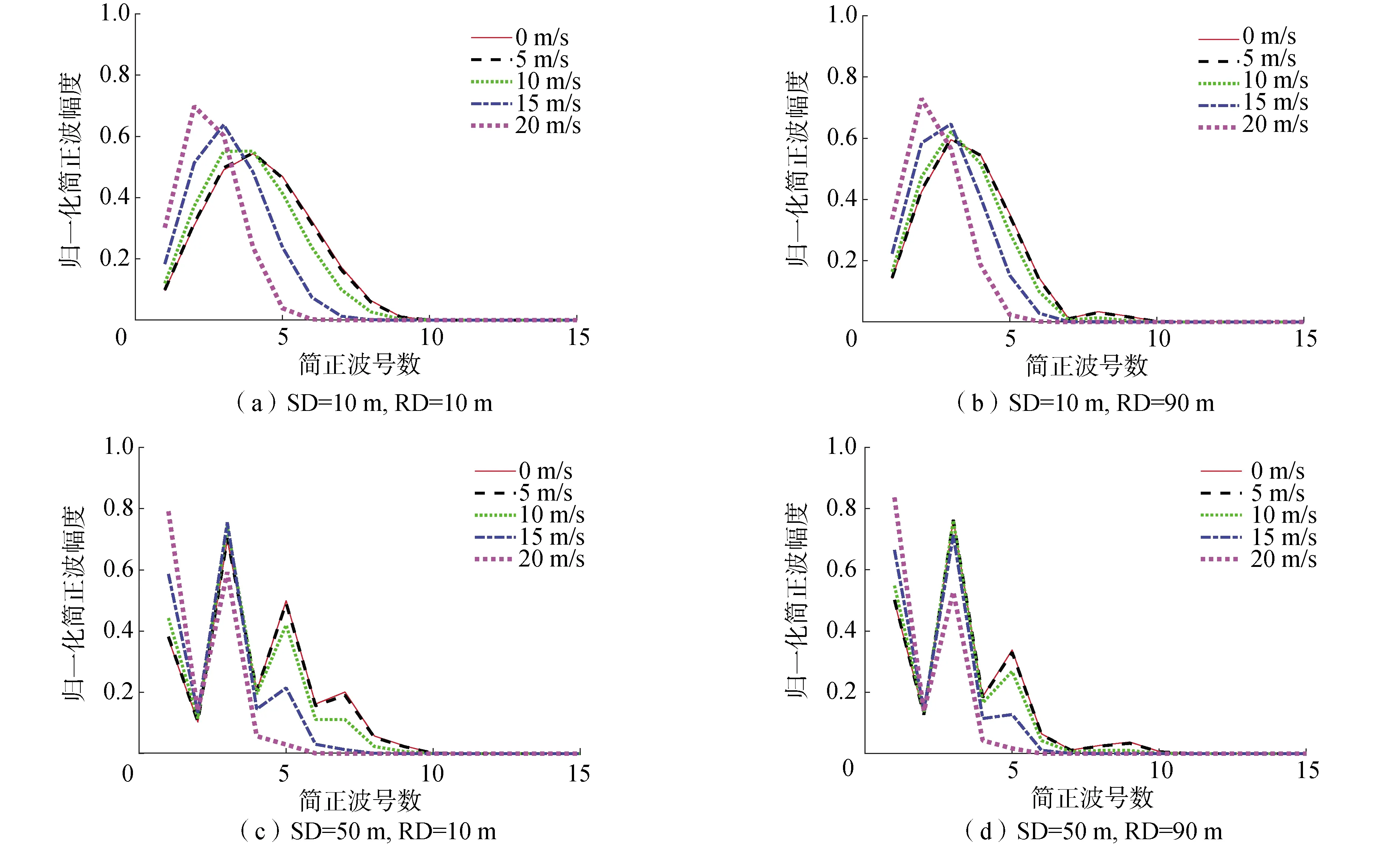
图8 不同海面风速下声场中各号简正波的归一化幅值的对比(R=20 km)Fig.8 Comparison of the normalization amplitude of each normal mode with different wind speeds (R=20 km)
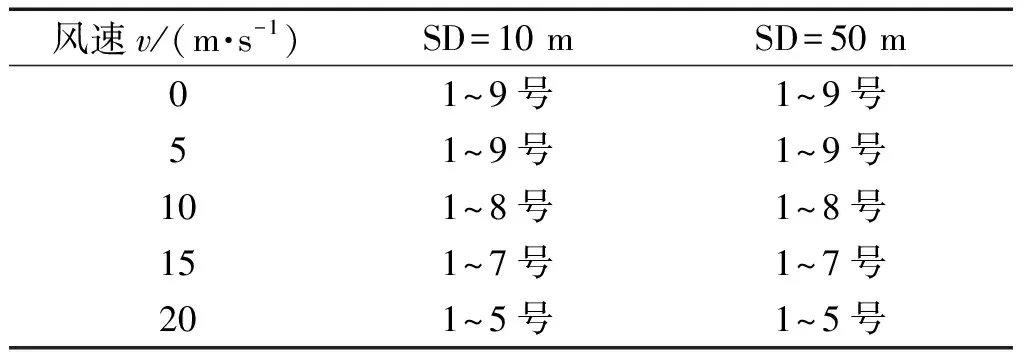
表1 不同海面风速v下的有效简正波号数统计(RD=10 m, R=10 km)
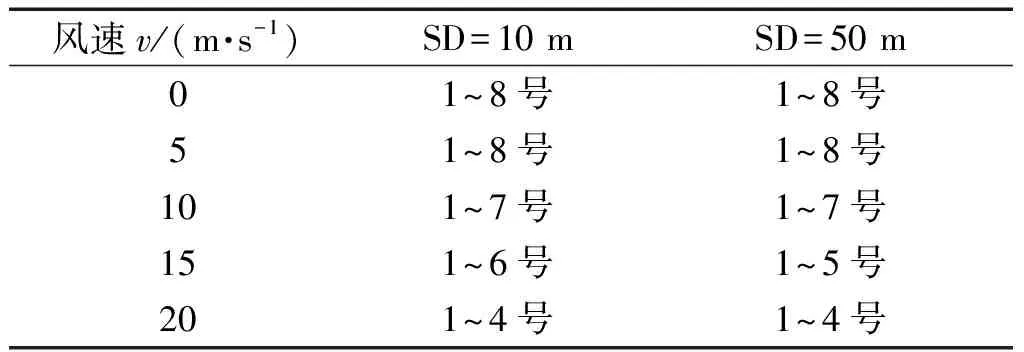
表2 不同海面风速v下的有效简正波号数统计(RD=10 m, R=20 km)
4 结论
1) 在给定的条件下,在一定的水平纵向间隔范围内,随着风速的增加,声场水平纵向相关性提高。由简正波理论可解释为:随着风速的增加,高号简正波衰减较快,声场中的有效简正波号数减少,导致声场中的简正波干涉减弱,进而导致声场水平纵向相关性的提升和水平纵向相关性振荡减弱。
2) 在同等风速条件下,在一定的水平纵向间隔范围内,随着水平距离的增加,声场水平纵向相关性提高。由简正波理论可解释为:随着水平距离的增加,高号简正波衰减较快,声场中的有效简正波号数减少,导致声场中的简正波干涉减弱,从而提高了声场水平纵向相关性。
3) 需要注意的是,本文重在探究粗糙海面引起的声信号能量的重新分布,以及这种重新分布下的声场空间相关性的改变,因此,没有考虑不同海面风速下的海面反射损失引起的信噪比的变化。
4) 本文研究的粗糙海面影响下的声场空间相关特性,可为风浪天气时的声场相关性预报等提供模型基础和算法支撑,不同风速下的仿真数值结果及海面风浪对声场水平纵向相关性的影响规律可为水平阵探测性能评估等提供数据参考。

