一般边界条件下矩形叠层板面内振动研究

蔡志东， 钟锐， 刘涛， 王青山

(1.中南大学 机电工程学院，湖南 长沙 410083； 2.中南大学 高性能综合制造国家重点实验室， 湖南 长沙 410083)

复合材料结构由于其高强度、高模量和低密度的特点，越来越被工程领域所重视，尤其在土木工程、车辆工程、海洋工程以及航空工程等领域被广泛运用[1-5]，而复合材料矩形叠层板结构作为基础构件，在工程领域的应用十分广泛。在实际应用过程中，矩形叠层板结构需要适应各种复杂工况，因此其在前期设计过程中的振动特性预测对于设计人员的工况匹配研究至关重要。目前，矩形叠层板结构自由振动特性的相关研究较多，但是大部分都是研究横向弯曲振动，对于高频的面内振动特性研究相对较少。然而在工程应用中，矩形板的面内振动也起着极为重要的作用，如直线型超声电机的研究[6]、超高速飞行器的研制、耦合板结构振动能量传输研究[7]等。因此，建立一种适用于一般边界条件下矩形叠层板结构的面内振动特性分析模型显得尤为迫切。

Bardell等[8]整理了板结构面内振动的研究文献，总结了几类经典边界条件下板结构的面内振动模态，并获得了精确的振动数据；Farag等[9]研究了对边固支边界条件下的板结构面内自由振动特性；Gorman[10-12]采用叠加方法对自由边界条件下弹性板面内振动固有特性进行了建模分析，并进一步对简支、固支以及弹性边界条件下板结构面内自由振动特性研究进行了拓展。史冬岩等[13]采用改进傅里叶级数法(improved fourier series method,IFSM)对矩形板在任意边界下的面内自由振动特性进行了研究，结合Rayleigh-Ritz法将矩形板的面内问题转变成了一个标准特征值求解问题。杜敬涛等[14]采用二维改进傅里叶级数方法对弹性板结构面内振动耦合位移场函数进行构建，并开展了相关试验测量进行验证分析。目前，对于矩形叠层板的自由振动分析也取得了较多的成果：费雷拉等[15]通过多二次径向基函数法和一阶剪切变形理论(first-order shear deformation theory，FSDT)求解运动方程，研究了对称层压复合板的自由振动。Ngo-Cong等[16]基于FSDT提出了一种径向基函数配置方法。Ye等[17]在FSDT的基础上，开发了一种修正的傅里叶解决方案，用于分析中等厚度的复合层板的自由振动；Qin等[18]提出了一种Jacobi-Ritz分析方法，用于在任意边界条件下对复合矩形叠层板的自由振动进行分析。

综上，目前对于矩形叠层板的面振动特性研究对于横向振动而言还相对匮乏，且已有的面内振动研究多集中于理论分析层面，相关实验研究较为少见。为此，本文基于能量法推导了矩形叠层板结构的控制微分方程，结合勒让德多项式和人工弹簧技术，建立矩形叠层板的数值分析模型。将求解结果与有限元法的结果进行对比，验证本文方法的正确性。同时，开展矩形板的面内振动试验，采用试验数据进一步验证本文方法的有效性。此外，本文针对矩形叠层板的面内振动特性展开参数化研究，分析比较纤维铺设角和纤维叠层数等参数对面内振动特性的影响，总结了各个参数对矩形叠层板的面内振动特性的影响规律。

1 矩形叠层板的模型建立

1.1 模型描述

图1所示为本文建立的一般边界条件下矩形叠层板面内振动模型，其长度为a，宽度为b，厚度为h，纤维层数为Nk，建立坐标系的x轴、y轴和z轴分别与该矩形叠层板的长、宽、高方向相重合。此外，θ表示矩形叠层板第k层的纤维基本方向与x轴之间的夹角。为了将矩形叠层板的面内振动模型统一化，采用人工弹簧技术，也就是图示中的2组线性弹簧系数(kt(t=u，v))对边界条件进行等效模拟，通过设置各边界约束弹簧的刚度值即可轻松得到不同的边界条件。

图1 弹性边界条件下矩形叠层板面内振动模型Fig.1 In-plane vibration model of laminated rectangular plate with elastic boundary conditions

1.2 模型描述

根据线弹性理论，矩形叠层板在任意点的法向应变和剪切应变可以表示为：

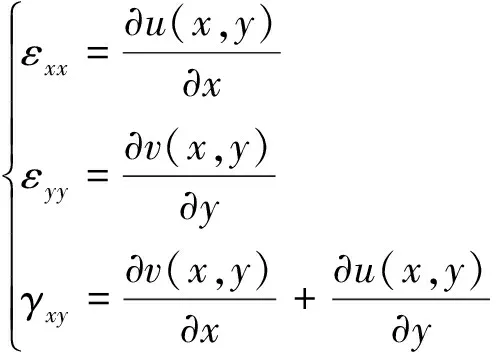
(1)

式中u(x,y)和v(x,y)分别为矩形叠层板在x方向和y方向的面内位移。在胡克定律的基础上，矩形叠层板的应力可以表示为：

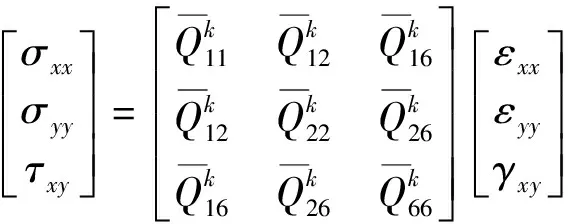
(2)

(3)

(4)

(5)

式中：Nxx和Nyy表示法向力；Nxy表示剪切力。

(6)

式中Aij表示延伸刚度，根据层弹性系数进行确定。

矩形叠层板的应变能可以表示为：

(7)

在本研究中，采用人工弹簧技术来等效处理一般边界条件。因此，与边界弹簧有关的势能为：

(ku,xLu2+kv,xLv2)|x=a]dy+

(ku,yLu2+kv,yLv2)|y=b]dx

(8)

式中：kt,x0、kt,xL、kt,y0和kt,yL(t=u，v)分别是边界x=0，x=a，y=0和y=b边界处的弹簧刚度。矩形叠层板面内振动引起的总动能为：

(9)

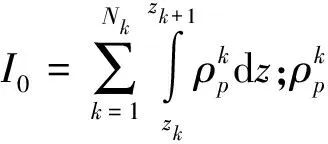
1.3 振动求解

在建立矩形叠层板的结构势能、结构动能以及边界势能的基础上，矩形叠层板的拉格朗日能量函数可以表示为：

L=T-U+V

(10)

在能量法求解过程中，位移容许函数对于结构振动特性的求解至关重要。常见的用于构建结构位移场的函数主要有改进傅里叶级数与正交多项式(即第一类和第二类切比雪夫多项式、勒让德多项式、特征正交多项式等)[19]，Qin等[19]在石墨烯圆柱壳的自由振动特性的研究中发现：正交多项式拥有相似的计算效率和收敛性，且都优于改进傅里叶级数。因此，对于矩形叠层板的面内振动的位移变量u(x,y)和v(x,y)，本文选取勒让德多项式进行表示：

(11)

(12)

式中：Umn和Vmn是未知的位移未知扩展系数；Pm(x)和Pn(y)分别是x方向上的阶数m和y方向上的阶数n的勒让德多项式；M和N分别代表Pm(x)和Pn(y)阶数的最大值。勒让德多项式的具体表达式为：

(13)

式中：i≥2；χ∈[-1,1]。

特别注意的是，由于勒让德多项式的求解区域与结构求解域不一致，因此在代入求解之前需要进行x=ξxχx+ζx和y=ξyχy+ζy的线性坐标变换，其中ξx=ζx=a/2，ξy=ζy=b/2。

在结构位移容许函数建立的基础上，将其代入方程(10)，采用里兹法位移未知扩展系数Umn和Vmn求极值即可获得矩形叠层板的面内振动特性求解方程：

(K-Mω2)A=0

(14)

式中：K、M和A分别表示刚度矩阵、质量矩阵和未知系数的向量。通过求解方程(14)，可以获得矩形叠层板的自然频率和相关特征向量，然后代入方程(10)即可获得相对应的面内振动模态振型。

2 数值与试验结果分析

本文已经对矩形叠层板的面内自由振动特性求解方程进行了描述，在获得理论推导的基础上，本文首先进行模型收敛性研究，确定边界刚度值与多项式截断值，随后开展数值仿真研究，并将计算结果与ABAQUS算得的结果和矩形板的面内振动试验结果进行对比。在此基础上展开参数化研究，讨论各参数对矩形叠层板面内振动特性的影响规律。

2.1 模型收敛性研究

正如前面的建模过程可知，对于矩形叠层板的边界条件模拟是通过在边界位置处引入了线性弹簧来进行等效处理。但是对于固定边界的等效需要设置一个合理大小的弹簧刚度值来进行近似处理，所以有必要开展边界刚度的收敛性研究，相关的计算结果如图2所示。在图2中，给出了2种纤维敷设方案的矩形叠层板，方案分别为[0°/30°/0°]和[45°/-45°/45°/-45°]。结构参数为1 m×1 m×0.05 m，材料参数为：E1=150 GPa；E2=10 GPa；G12=5 GPa；G13=5 GPa；G23=6 GPa。ku和kv分别代表矩形叠层板沿x轴与y轴方向的边界刚度值，坐标值分别取以10为底ku和kv的对数值，采用等高线云图表现频率的收敛性，刚度值分别从104变化到1014。

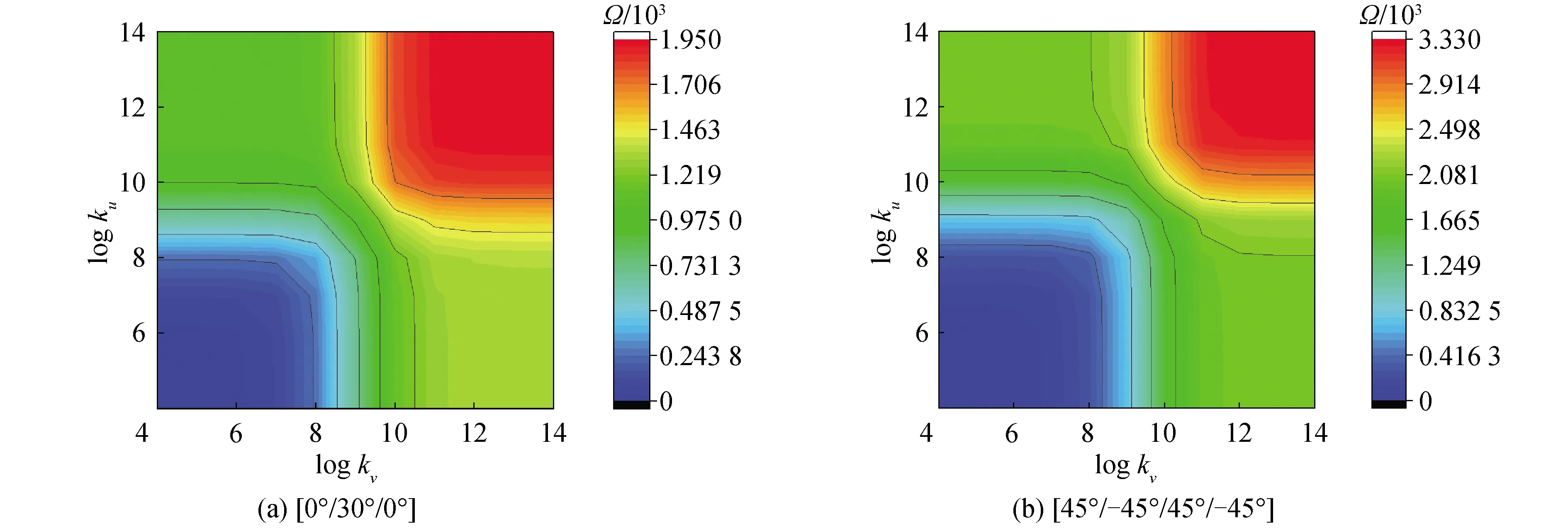
图2 边界刚度值收敛性分析Fig.2 Convergence analysis of boundary stiffness value

从图2中可以看出，当边界弹簧ku以及kv的刚度值在107～1010N/m内变化时，频率参数随之变化(图中绿色区域)，此时可将其定义为弹性边界(E)；而当结构的边界刚度值在1010～1014N/m变化时，频率参数已基本收敛(图中红色区域)，对应的边界可视为固定支撑边界(C)；而刚度值为0时(图中蓝色区域)，可将边界定义为自由边界(F)。

接下来，开展勒让德多项式收敛性研究，将截断值M和N从2取值到12得到的收敛性结果如图3所示，结构边界条件分别为C-C-C-C、F-F-F-F和C-F-C-F边界，结构参数和材料参数与图2保持一致，纤维敷设角度为[45°/-45°/45°/-45°]。从图中可以看出，随着截断值M和N的增加，计算结果迅速收敛，当截断值达到12时，与截断值为10时的误差均小于0.5‰。虽然从理论上讲，当截断值无限大时，计算结果可以完全等于精确分析结果。但是，考虑到实际的硬件计算资源和计算效率，通常需要选择一个合理的截断值。因此，在后续算例分析中，勒让德多项式的截断值选定为M=N=12。

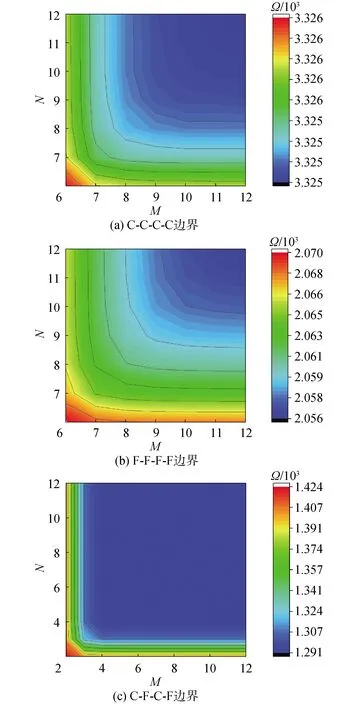
图3 勒让德多项式截断值收敛性分析Fig.3 Convergence analysis of truncation value of Legendre polynomial

2.2 模型正确性研究

表2给出了矩形叠层板在本文求解分析模型和有限元分析模型下所获得的前6阶自然固有频率，结构参数和材料参数与图2保持一致。对于结构振动特性而言，模态振型可以直观反映出结构的固有特性，因此图4还给出了本文方法与有限元法所得到的模态振型对比图。通过表1数据和图4可知，采用本文方法计算所得的数值与ABAQUS仿真得到的结果吻合较好，数值误差较小。因此，可以验证本文所提出的方法对矩形叠层板面内自由振动计算的有效性。

为了进一步验证该模型的正确性，本文开展了实验对比分析，搭建了如图5中所示的振动试验系统。试验件采用铝板材激光加工而成，尺寸为a×b×h=1 250 mm×1 127 mm×10 mm，弹性模量为E=70 GPa，泊松比μ=0.33。在铝板顶边两端加工有2个吊装孔，通过弹性绳将矩形铝板吊装在台架上，从而实现了试验件的自由约束边界条件设置。测试方法选用单点面内激励多点拾振，激励点选择为1号测点的x方向，将矩形铝板的表面被均匀划分为10×10个网格，共计121个测点，在测点处布置三向加速度计，按照编号依次挪动传感器位置测量各测点的响应数据。

对于每次测量采用力锤进行敲击，拾取被测点x、y方向上的振动响应信号，并保存在数据与采集分析系统中，力锤敲击的激励力信号数据也被同步保存在系统中。每个测点测量5次数据，系统自动求取平均值进行数据处理，以减少试验误差。测试完成后，通过东华DHDAS软件辅助工具处理试验中产生的激励与响应数据，最终可以得到该矩形铝板的面内模态试验结果。

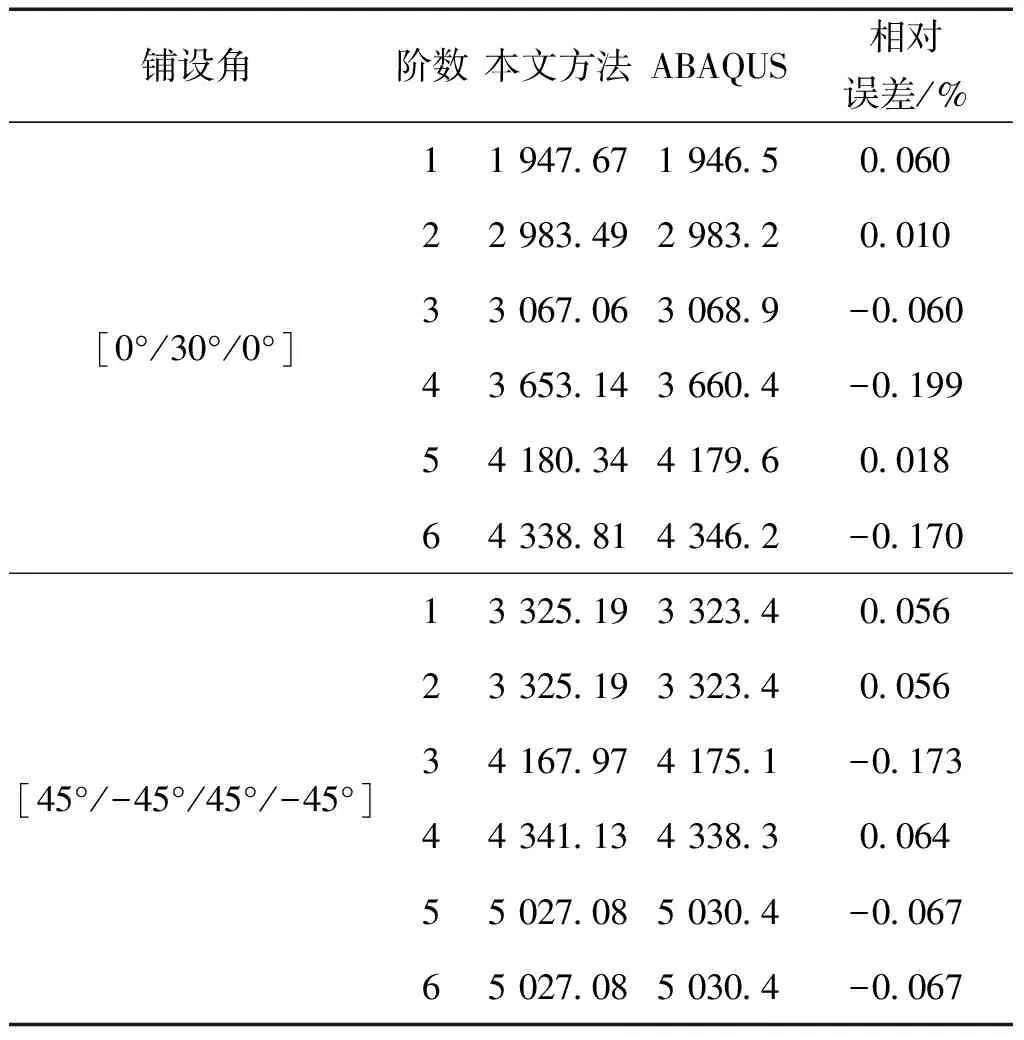
表1 固支边界下矩形叠层板固有频率参数对比

采用本文方法预测与试验测试的得到前8阶面内模态频率对比如表2所示。通过表2可知，采用本文方法得到预测值也可以很好地与试验测量值吻合，前8阶面内模态频率的误差普遍在1%以内，最大误差不超过2%。综合分析试验结果，可以进一步论证本文所建立的矩形叠层板面内自由振动模型的准确性。

图4 本文方法与有限元法得到的前3阶阵型图对比Fig.4 Comparison of the first three-order array diagram obtained by present method and the finite element method

图5 矩形板面内振动模态测试系统Fig.5 In-plane vibration mode test system of rectangular plate

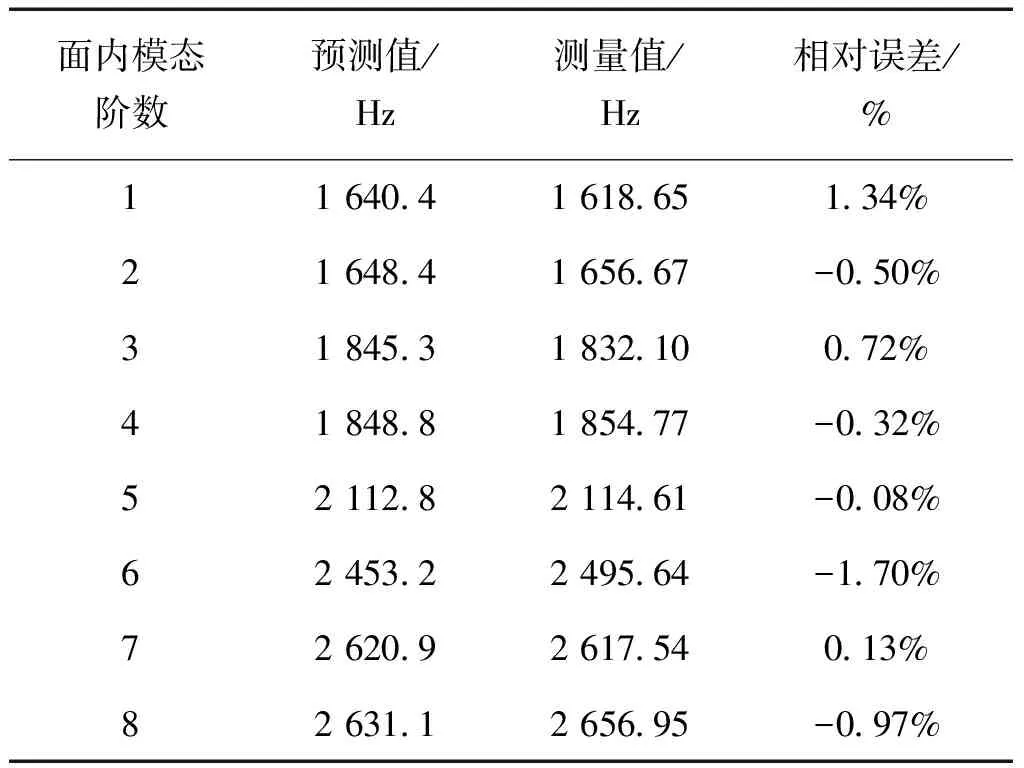
表2 前8阶面内模态频率预测与测量结果对比

2.3 参数化研究

通过现有文献调研可知，对于矩形叠层板振动特性研究目前大多数都是研究低频的弯曲振动，对于高频振动的面内自由振动的研究还十分鲜有。因此为了丰富现有研究成果，本小节在上述收敛性和有效性研究的基础上，进一步开展参数化研究，主要包括纤维铺设角和纤维叠层数等因素。

为研究材料纤维铺设角的变化对矩形叠层板振动特性的影响，选取了2组纤维铺设方案：[0°/α°/0°]和[0°/α°/0°/α°]，其中敷设角度α°从0°到90°变化。对于每种敷设方案，选取了3种不同的边界条件CCCC、FFFF和CFCF，几何和材料属性与表1相同，选取前3阶模态频率进行参数化结果展示，如图6所示。从图中可知，各边界下2种不同铺设方案的铺设角变化对结构面内振动频率的影响具有相似的规律，且对于CCCC及CFCF边界，频率随着铺设角的增大，总体上呈现出增大的趋势，而对于FFFF边界，其变化大体是先增大后减少的趋势，这主要是由于不同边界条件对于结构的刚度影响存在差别引起的。

为研究纤维层数对矩形叠层板面内自由振动的影响，对不同纤维层数下的面内自由振动频率进行分析计算。如图7所示，矩形叠层板采用奇数层纤维铺设角度为0°，偶数层层数的纤维铺设角为90°的纤维铺设方案，随着纤维层数Nk取值的不同，纤维敷设层数也随着发生相应的变化，结构边界条件分别为CCCC、FFFF和CFCF，选取前3阶模态频率进行参数化结果展示。从图7中可以看出，随着纤维层数的增大，偶数层的模态频率保持一致，这是因为刚度系数不随偶数层数目Nk的变化而改变。而奇数层的改变，会导致刚度系数随之发生变化，因此其对应的频率参数也会发生相应的波动。

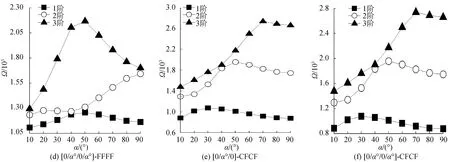
图6 不同纤维敷设方案前3阶面内频率随铺设角变化规律Fig.6 Variation of frequency parameters with laying angle under different lamination schemes

3 结论

1)对比分析3种方法得到的数据结果，证明了本文计算方法的正确性和有效性。

2)由于不同边界条件对于结构的刚度影响，矩形叠层板的纤维铺设角变化对结构面内振动频率有较大影响。

3)矩形叠层板的频率参数会随着铺设层数的变化而发生波动。

4)通过本文的研究可以对未来进一步的更复杂的复合材料结构在高频区域的振动特性研究提供一定的理论基础。