基于启发式深度Q学习的多机器人任务分配算法
张子迎, 陈云飞, 王宇华, 冯光升
(1.嘉应学院 计算机学院,广东 梅州 514015; 2.哈尔滨工程大学 计算机与科学技术学院,黑龙江 哈尔滨 150001)
随着人工智能的发展,多机器人任务分配或任务调度[1-3](multi-robot task allocation,MRTA)技术受到人们广泛的关注,而多机器人任务分配算法的准确性和时效性直接影响了完成任务所产生的代价,具有很高的实际研究价值,近年来国内外很多学者对此进行了深入的研究[4-6]。
强化学习作为多机器人任务分配领域的一个重要研究方向,主要利用智能体与环境的实时交互和错误判断机制,获得累积最大奖赏值的方式,训练出算法的最优动作决策序列[7-8]。随着强化学习相关应用领域的快速发展,强化学习在解决单机器人智能决策问题上取得了辉煌的成就[9]。传统的强化学习都是应用于单机器人决策,如何将单智能体强化学习应用到多机器人强化学习中,国内外学者进行的大量的探索,主要的实现方法为基于值函数。基于值函数的多机器人强化学习算法主要包括Q学习(Q-Learning)、分层强化学习(hierarchical reinforcement learning, HRL)和深度Q学习(deepQnetwork, DQN)算法[10-12],算法通过结合值函数和奖励函数来模拟多机器人强化学习中机器人之间的协作和竞争,进而达到全局最优的策略效果。
针对复杂环境下分层强化学习处理多机器人任务分配存在的维度灾难问题。本文提出一种启发式深度Q学习(heuristically accelerated deepQnetwork,HADQN)算法解决复杂环境下多机器人任务分配的问题。该算法采用神经网络进行Q值的存储和计算,一定程度上避免了强化学习的维度灾难问题;同时引入轨迹池机制和动态探索因子,在提高算法学习效率、探索能力的同时,保证了算法的收敛性。
1 基于HADQN算法的MRTA算法研究
本文提出了可以处理实际应用场景的基于HADQN的多机器人多任务分配算法。如图1为HADQN算法在传统DQN算法的基础上引入了轨迹池更新经验池中的数据,促进了DQN算法对轨迹池中有效动作的选择。
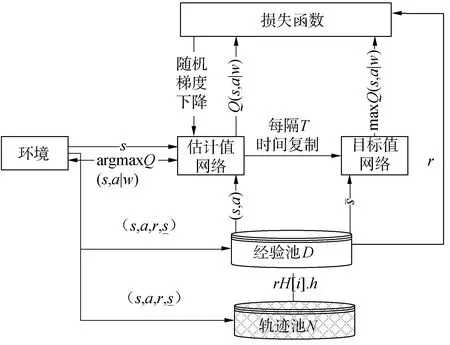
图1 HADQN模型示意Fig.1 Schematic diagram of HADQN model
为了更加全面的对HADQN算法的运行机理研究,本文从状态-动作空间定义、动作选择策略、奖赏函数设计、网络结构设计和HADQN算法在MRTA中的应用等5个方面进行介绍。
1.1 状态-动作空间定义
本文采用HADQN算法处理多机器人多任务分配问题,针对实际的应用环境对HADQN算法的状态空间和动作重新进行定义。
1)首先本文所提算法在栅格化地图上进行验证,因此可以进行各个机器人位置信息的设置,定义机器人Ri的位置坐标为pi=(pi.x,pi.y),i∈{1,2,…,n}(n为环境中机器人的数目)。pi.x∈{1,2,3…,X}(X为当前实验地图的宽度值),pi.y∈{1,2,3…,Y}(Y为当前实验地图的高度值)。
2)其次定义状态空间,状态空间要包含当前环境中的所有可能情况,即包括所有机器人的位置信息、任务点的位置信息和任务点的完成状况。因此结合环境定义HADQN算法的状态空间S:
S=(R1,R2,…,Rn,g1,g2,…,gm)
(1)
式中gj为任务点j的完成情况,gj∈{0,1}(0表示该任务点j未完成,1表示该任务点j已经完成)。
3)最后定义动作空间,根据环境中的机器人位置信息定义HADQN算法的动作空间A:
A=(a1,a2,…,an)
(2)
式中ai为机器人i选择的动作,ai∈{TOP,BOTTOM,LEFT,RIGHT,CENTER},其中TOP表示机器人向上移动一个单位;BOTTOM表示机器人向下移动一个单位;LEFT表示机器人向左移动一个单位;RIGHT表示机器人向右移动一个单位;CENTER表示机器人保持当前位置不动。
1.2 动作选择策略
针对ε-greedy算法探索因子ε取值的问题,提出了一种动态调整ε的动作选择策略。即在算法初期,将探索因子ε设置较低的值,保证算法对环境中未知空间的探索;随着迭代次数的增加,算法对环境的认知能力加大,不断增加探索因子ε的值,提高算法对已学习经验的利用率;同时设置探索因子ε的最终值,促进算法对已学习经验的利用(如图2)。
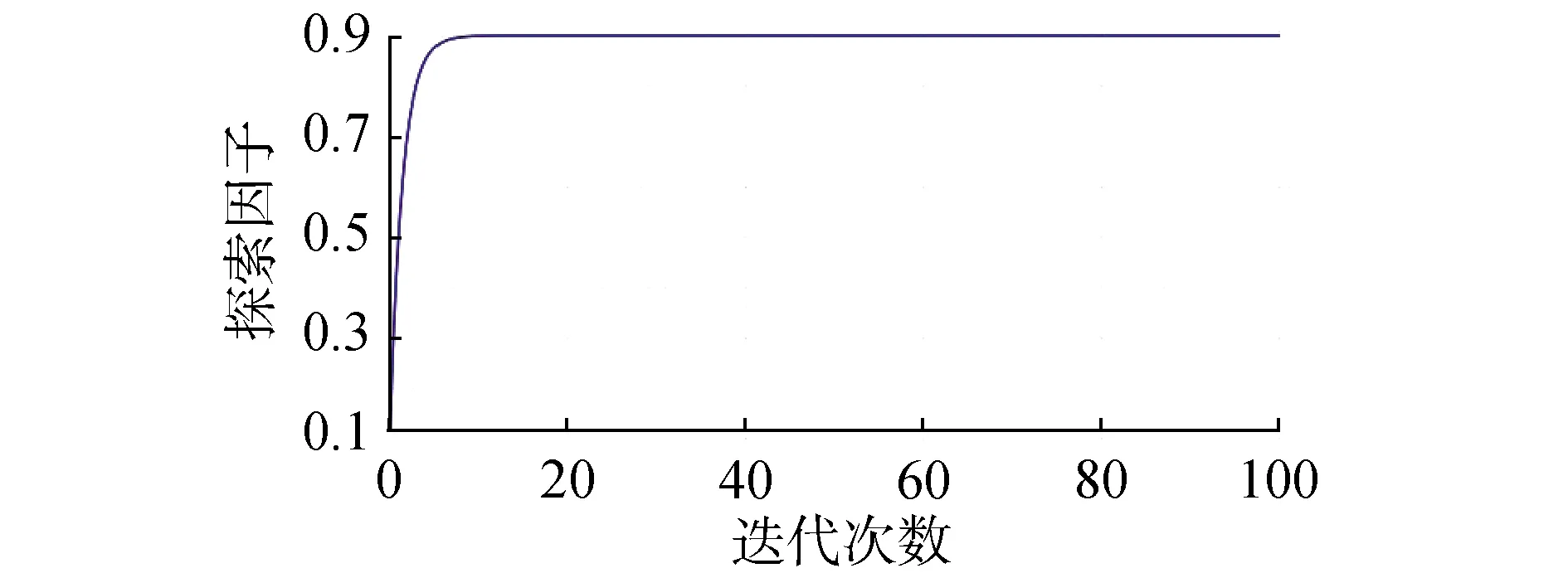
图2 探索因子ε随着迭代次数episode的变化趋势Fig.2 Exploratory factor ε change trend graph with the number of iterations
探索因子ε的定义为:
(3)
式中:εmax为一个实数代表探索因子ε的最大值,可设置范围0≤εmax<1;ε0为一个实数代表探索因子ε初始值,可设置范围0≤ε0≤εmax;episode为整数变量代表算法当前迭代次数,episode的变化范围为[0,max_episode];max_episode为一个正整数代表算法最大迭代次数;ζ为一个实数代表动态系数,可设置范围0<ζ<1。
其中设置探索因子最大值εmax等于0.9,探索因子初始值ε0为0.1,最大迭代次数max_episode为100,动态系数ζ为0.8。
1.3 奖赏函数设计
奖赏函数为环境中的机器人在当前状态下执行某一动作的回报值,也即对此时的状态-动作对进行的好坏评价标准。本文中,由环境中所有机器人选择的动作组成的联合动作就是算法所提的联合动作。环境中有多个任务点,只有当环境中所有任务点均完成整个任务分配过程才结束。针对以上问题,首先将环境中的状态分为如下4类:
1)游离状态(YS):所有机器人均未与障碍物发生碰撞,同时所有机器人也均未到达任一任务点;
2)半成功状态(MS):存在机器人达到任务点,但环境的尚存在未完成任务点;
3)失败状态(FS):存在机器人与障碍物发生碰撞;
4)完成状态(WS):环境中所有的任务均已完成。
根据上面的分类,可以将多机器人多任务点环境的当前状态分类表示为:
S=[YS,FS,MS,WS]
(4)
在状态分类的基础上,可以定义奖励函数为:
(5)
式中ns代表环境转移到当前状态s此步完成任务点的数目。
1.4 网络结构设计
在解决多机器人多任务分配问题的复杂环境中,DeepMind团队提出DQN算法中采用Q值来训练神经网络,进而用训练好的神经网络来代替Q值表。即利用神经网络来近似代替Q值表,完成Q值的计算,参数为w的Q网络Q(s,a|w)的定义为:
Q(s,(a1,a2,…,an)|w)≈Qπ(s,(a1,a2,…,an))…
(6)
本文设计的Q网络输入值为状态空间,输出的为该状态空间下所有联合动作空间的Q值。
如图3通过把当前状态s作为输入值,S=[R1,R2,…,Rn,g1,g2,…,gm],在多机器人多任务中状态s为n+m维状态空间即,输出向量为该状态下所有联合动作(a1,a2,…,an)的Q值:[Q(s,(a1,a2,…,an)1),Q(s,(a1,a2,…,an)2),…,Q(s,(a1,a2, …,an)m)]。

图3 使用Q网络实现从状态到联合动作的映射Fig.3 Use Q network to realize the mapping from state to joint action
在本文HADQN算法采用的DQN算法的神经网络分布结构,利用2个结构相同,但参数不同的神经网络Q_target网络和Q_eval网络。其中只利用Q_eval网络参与每次的算法训练并进行参数更新,而Q_target网络则并非每次都参与算法的训练而是每隔一定的时间将Q_eval网络的参数直接复制给Q_target网络。针对偏差问题,设置Q_eval网络的参数更新损失误差函数L(w):
Q(s,(a1,a2,…,an)|w))2]
(7)

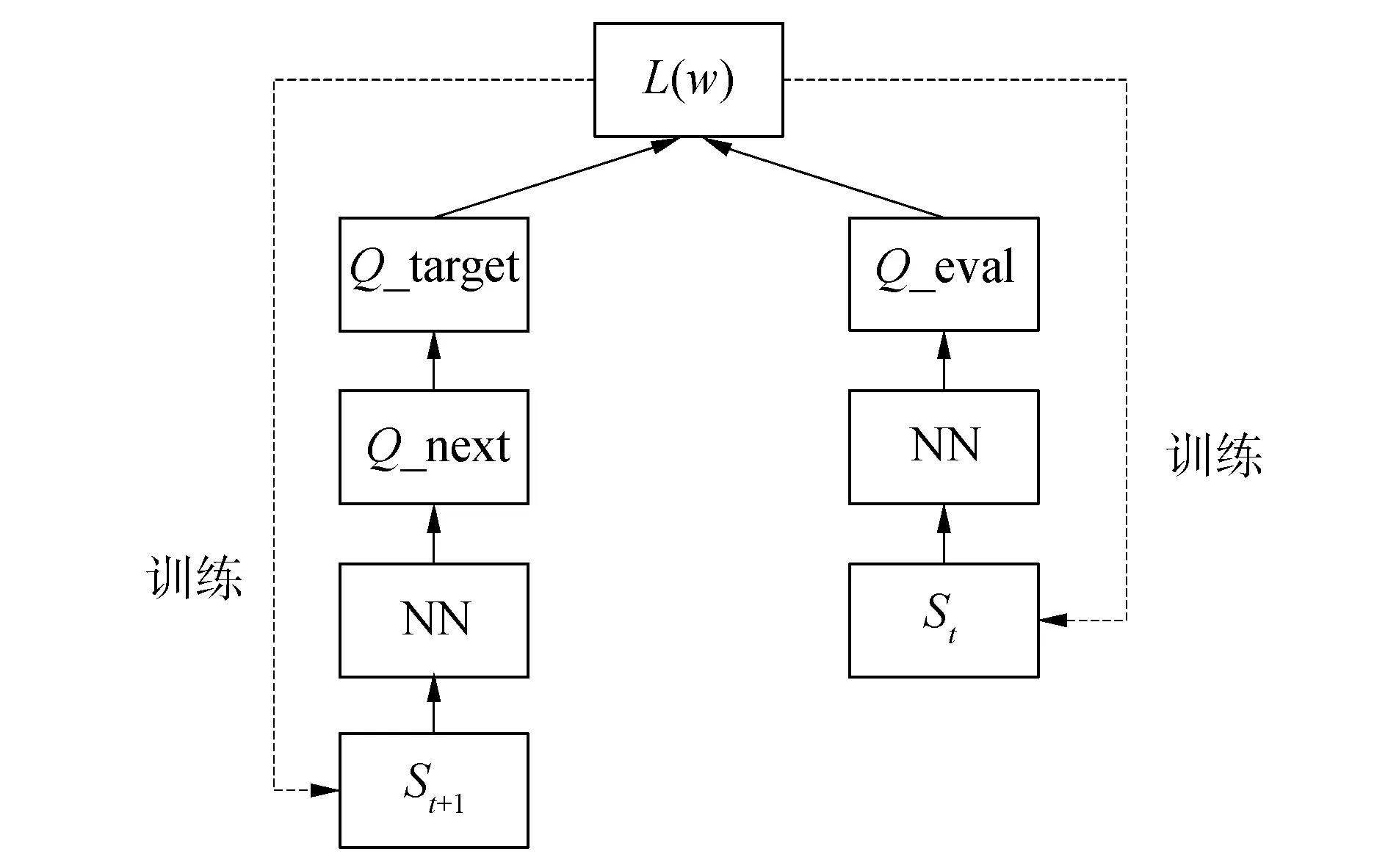
图4 Q网络流程示意Fig.4 Q network process diagram
1.5 HADQN算法在MRTA中的应用
针对传统算法存在学习效率低的问题,本文采用引入动态探索因子,并创建了启发式奖励值更新的策略,提出了HADQN算法。根据算法的学习过程将多机器人多任务分配问题分为2个阶段:
1)初始阶段,将探索因子ε设置比较小,保证算法初始阶段对环境中未知空间的探索性;
2)收敛阶段,设置探索因子ε为一个较大的数(本文设置ε=0.9),保证算法对已学习经验的利用。为了保证算法对已经历动作的充分利用,本算法采用轨迹记录的方法,将动作得到的奖励值一定的比例回馈给该路径上的其他动作。
根据HADQN算法在多机器人多任务分配的实际场景结合式(3)定义的动态探索因子ε定义该算法的动作选择策略πD(s):
(8)
式中:q为0~1的随机数;Q(s,a1,a2,…,an|w)为在线更新Q网络;w为Q网络的权重。
本文定义轨迹池用来存储该路径点距离当前状态点的迭代次数信息,轨迹池H定义为:
其容量和经验池容量N相同的,在轨迹池中5个变量共同定义了算法某一路径点的全部信息。每轮迭代轨迹池H的更新方式为:
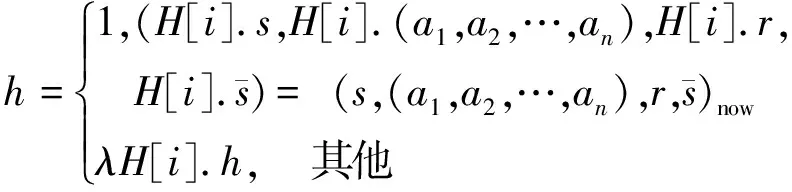
(9)
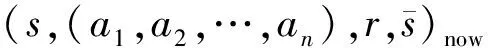
根据轨迹池的定义,修改经验池的更新方式:

(10)
式中:index为新的状态元组加入经验池D中的索引;η为启发因子。采用贝尔曼方程计算得到在HADQN算法中目标函数:
(11)
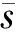
2 仿真实验结果与分析
2.1 实验参数
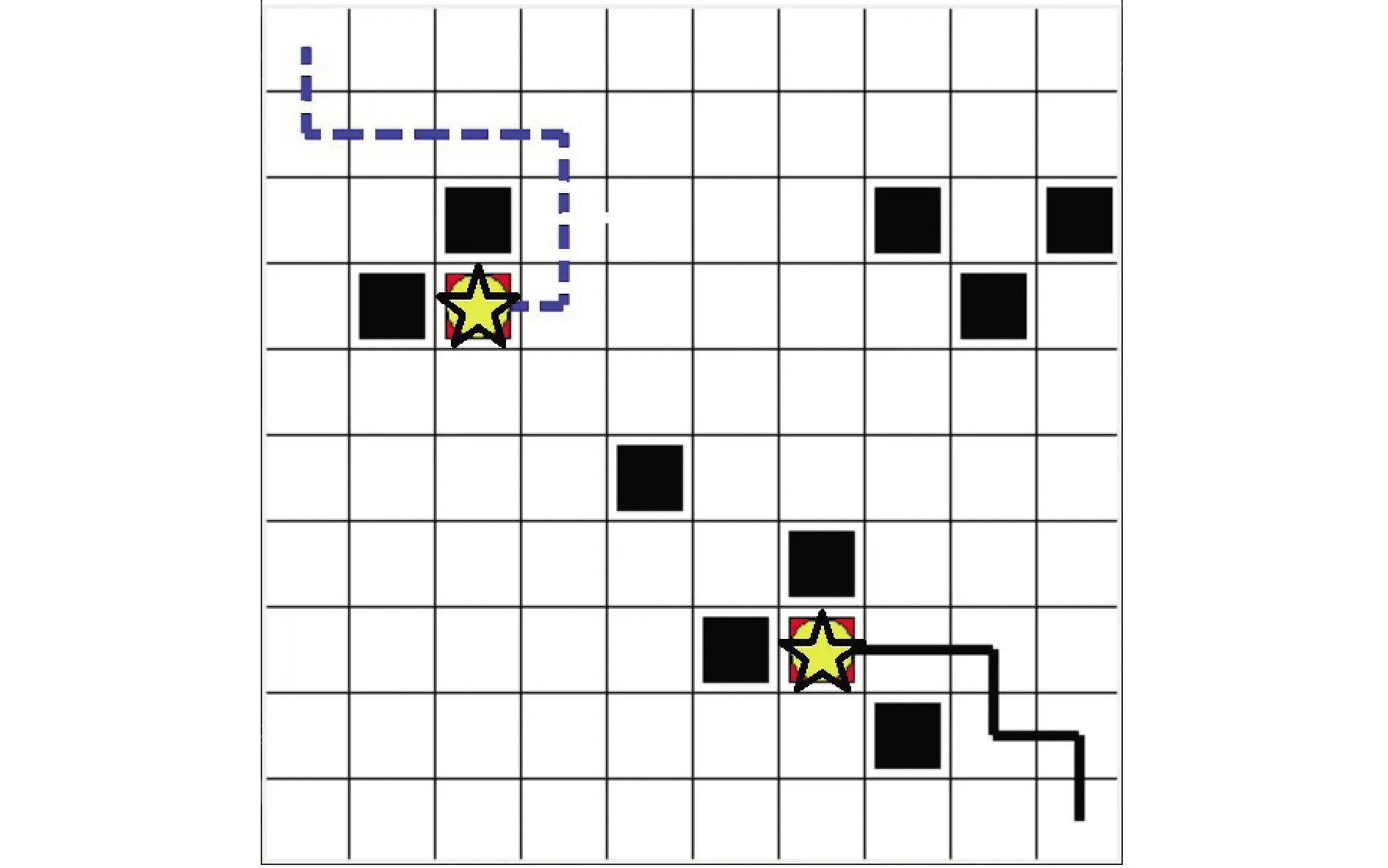
本文将实验场景离散化为10×10的栅格化地图进行仿真实验。HADQN算法仿真实验基础参数设置如表1所示,部分参数根据不同的实验场景进行单独设置。

表1 仿真实验参数设置表Table 1 Simulation experiment parameter setting table
2.2 实验效果
为了充分证明本文提出的基于HADQN的多机器人任务分配算法的正确性和适用性,本文从机器人数目和任务点数量的角度将多机器人任务分配系统分为机器人数目大于目标点数目、机器人数目等于目标点数目和机器人数目小于目标点数目3种情况。
2.2.1 实验1:机器人数目大于任务点数目
本节通过多轮仿真实验对比,最终选定如下核心参数进行实验1仿真效果的展示。

表2 核心参数设置表(实验1)Table 2 Core parameter setting table (Experiment 1)
如图5所示为在环境中机器人小于任务点数目的情况下,任务分配算法训练过程中,奖励值和完成所有任务消耗步数数据变化趋势图。由图5(a)所示在训练的初期奖励值为震荡状态,当迭代次数为750时算法收敛,奖励值稳定于19.73附近。如图5(b)算法在迭代1 800次后收敛,奖励值稳定与19.73附近。如图5(c)算法训练初期机器人消耗大量的步数探索空间,随着不断训练机器人完成系统中所有任务消耗的步数逐渐减小,并在迭代750次时收敛于10。如图5(d)算法在迭代1 800次后收敛,消耗步数收敛于10。由图5综合分析,基于HADQN的任务分配算法在成功解决了机器人数目大于目标点数目情况下的多机器任务分配问题并稳定收敛于最优解附近。同时对比与基于DQN的任务分配算法,基于HADQN的任务分配算法在保证收敛结果最优的情况下,提高了算法的收敛速度。

图5 任务分配算法训练过程(机器人数目大于任务点数目)Fig.5 Task distribution algorithm training process diagram(the number of robots is greater than the number of task points)
如图6所示系统中的机器人数目大于目标点数目时,会选择距离任务点更近的机器完成相应的任务,进而保证机器人完成系统中所有任务所消耗的步数最少,同时能够成功的避开环境中的障碍物。通过实验验证了本文所提算法的正确性。在收敛速度方面,基于HADQN的任务分配算法相对于基于DQN的任务分配算法收敛速度提高了1.4倍。

注:☆表示机器人,■表示障碍物,○表示目标点,---表示移动路线。 图6 任务分配结果(机器人数目大于任务点数目)Fig.6 Task distribution result map (the number of robots is greater than the number of task points)
2.2.2 实验2:机器人数目等于任务点数目
本节通过多轮仿真实验对比,最终选定如下核心参数进行实验2仿真效果的展示。

表3 核心参数设置表(实验2)Table 3 Core parameter setting table (Experiment 2)
如图7(a)所示,在训练的初期奖励值为震荡状态,随着迭代次数的增加奖励值逐渐震荡增加,当迭代次数为1 000时算法收敛,奖励值稳定于29.91。如图7(b)所示,算法在迭代2 600次时收敛于29.85。如图7(c)所示,在算法训练初期机器人消耗大量的步数探索空间,随着迭代次数的增加,机器人完成系统中所有任务消耗的步数逐渐减小,并在迭代1 000次时收敛于7左右附近。如图7(d)基所示,算法在迭代2 600次时收敛于11。综合分析图7可知,基于HADQN的多机器人任务分配算法在该环境下,能够在短时间内完成对环境的探索,并稳定收敛于最优解。同时相对于基于DQN的多机器人任务分配算法,本文所提算法在收敛速度和训练结果均优于基于DQN的多机器人任务分配算法。

图7 任务分配算法训练过程图(机器人数目和任务点数目相等)Fig.7 Task distribution algorithm training process diagram (the number of robots is equal to the number of task points)
由图8可知,系统中的机器人在面对多个任务需要完成时,会选择距离各个机器人所在位置近的任务点进行完成,进而保证机器人完成系统中所有任务所消耗的步数最少,同时机器人能够成功的避开环境中的障碍物。实验证明,在收敛速度方面,基于HADQN的任务分配算法相对于基于DQN的任务分配算法收敛速度提高了1.6倍。
注:☆表示机器人,■表示障碍物,○表示目标点,---表示移动路线。 图8 任务分配结果图(机器人数目和任务点数目相等)Fig.8 Task distribution result graph (the number of robots is equal to the number of task points)
2.2.3 实验3:机器人数目小于任务点数目
本节通过多轮仿真实验对比,最终选定如下核心参数进行实验3仿真效果的展示。
由图9(a)分析可知,在算法初期0~2 000次迭代中,奖励值一直处于震荡状态,算法在迭代2 000次时完成收敛并稳定于398附近。如图9(b)所示,算法在迭代5 500次时收敛于396.2。图9(c)在算法初期机器人换成系统中所有任务所消耗的步数比较大,随着算法迭代次数的增加,机器人所消耗步数逐渐减小,迭代2 000步时收敛于11。如图9(d)所示,算法在迭代5 500次时收敛于20。综合对比图9可知,基于HADQN的多机器人任务分配算法相对于基于DQN的多机器人任务分配算法在收敛速度上明显提升,同时任务分配结果更优。
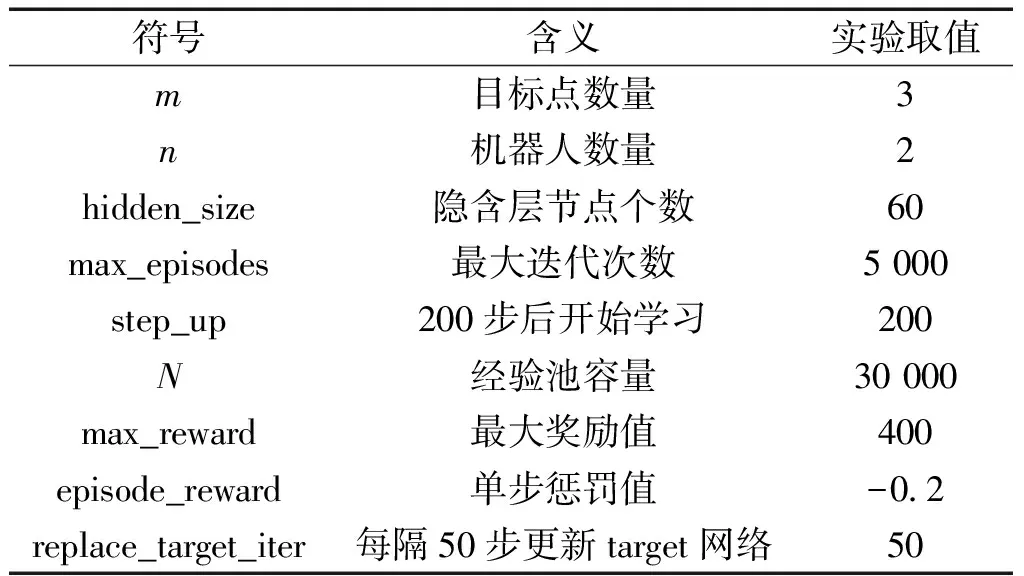
表4 核心参数设置表(实验3)Table 4 Core parameter setting table (Experiment 3)
由图10分析可知,系统中的机器人已经成功完成了系统中的所有任务,并根据机器人和目标点的相对位置选择消耗步数最少的任务分配方案进行任务的分配。实验证明,基于HADQN的任务分配算法在机器人数目小于任务点数目的情况下,算法能够成功的完成机器人的任务分配问题,并提供机器到达目标点的路径规划功能(避开环境中的障碍物)。在收敛速度方面,基于HADQN的任务分配算法相对于基于DQN的任务分配算法收敛速度提高了1.75倍。

图9 任务分配算法训练过程图(机器人数目小于任务点数目)Fig.9 Task distribution algorithm training process diagram (the number of robots is less than the number of task points)
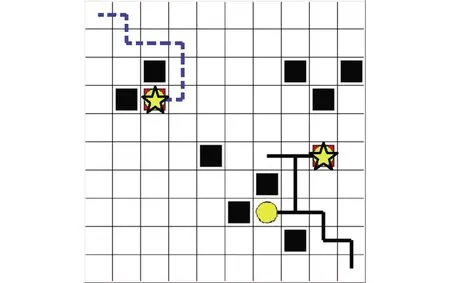
注:☆表示机器人,■表示障碍物,○表示目标点,---表示移动路线。 图10 任务分配结果图(机器人数目小于任务点数目)Fig.10 Task distribution result graph (the number of robots is less than the number of task points)
本文所提的基于HADQN的多机器任务分配算法相对于传统的于DQN的多机器人任务分配算法在收敛速度和分配结果均存在一定程度的优化。
3 结论
1)该算法采用神经网络来解决复杂环境下多机器人任务分配中的维度灾难问题,并在传统DQN算法的基础上引入了动态动作选择策略和启发函数。
2)采用动态动作选择策略保证了算法前期对环境中未知空间的探索能力。
3)采用启发函数启发DQN算法动作选择,提高DQN算法对成功经验的学习和积累能力,提高算法的学习效率,进而加快算法的收敛速度。
4)通过仿真实验与基于DQN的多机器人任务分配算法进行实验对比,相对于传统的基于DQN的多机器人任务分配算法,基于HADQN的多机器人任务分配算法加快了收敛速度和优化了任务分配结果。
5)通过本文的理论推导和仿真实验验证,证明了HADQN算法在解决多机器人多任务分配问题上的实用性和鲁棒性。

