基于迁移学习的小样本垂直阵目标距离估计方法
姚琦海, 汪勇, 杨益新
(1.西北工业大学 航海学院, 陕西 西安 710072; 2.陕西省水下信息技术重点实验室, 陕西 西安 710072)
水下目标定位是水声信号处理领域的热点,其中被动定位技术凭借其优良的隐蔽性,在军事和民用领域中有着广泛的应用[1-3]。传统的被动定位方法大多为基于水声模型的匹配场处理(matched field processing,MFP),Bucker[4]提出了线性匹配场处理器,并建立实际环境模型,通过计算距离-深度的模糊函数实现被动定位。Baggeroer等[5]建立基于水平分层海洋环境波导模型的匹配场处理技术,得到增加带宽可以有效提高匹配场算法的准确度。Michalopoulou等[6]通过非相关方法叠加各个频点的窄带模糊度函数,得到非相关方法在宽带匹配场处理算法中具有可行性。Soares等[7]基于各个频点之间的相关性,设计了归一化相关处理器和匹配相位相关处理器。杨坤德等[8]在环境失配条件下强干扰的场景中,设计了一种线性匹配场处理算法,从而实现干扰的抑制。匹配场处理方法基于水声信道特性将声传播模型和阵列信号相结合,实现对水下目标深度和距离的估计,但其定位性能严重依赖海深、声速剖面等参数,在强干扰和环境失配的场景中,该方法的准确度会受到严重影响。
数据驱动模型不依赖海洋环境参数,以神经网络为代表的数据驱动方法在水声被动定位领域得到了广泛的应用。Steinberg等[9]针对均匀介质中的点声源,建立单层神经网络模型,从而实现深度估计。但当时机器学习技术较为薄弱,未得到广泛的应用,以及主流被动定位算法是匹配场处理方法,因此,在水声被动定位领域,机器学习方法很长一段时间的发展较为缓慢。Wang等[10]在水声被动定位领域引入了广义回归神经网络方法,在浅海高信噪比的环境中,得到该方法可实现有效的目标距离估计。Liu等[11]基于一维卷积神经网络(convolutional neural network,CNN)和集成学习技术,在深度范围大致确定的场景中,实现了水下目标距离估计。姚琦海等[12]建立经优化的广义回归神经网络模型,在浅海强干扰的环境中,有效实现水下目标距离估计。以上研究利用卷积神经网络、支持向量机等模型对水下单目标进行了位置估计,取得了较好的效果。
迁移学习是对不同但相关领域问题利用已存有的知识进行求解的一种机器学习方法[13]。在图像处理领域,迁移学习已有大量的应用。Dai等[14]基于迁移学习模型,借助文本数据来辅助图像聚类,可得到该方法可有效地提高图像聚类的准确度。Zhu等[15]将图像上的标签信息作为图像与文本之间知识迁移的桥梁,有助于提高图像分类的效果。而迁移学习在水声定位领域的应用较少。Wang等[16]通过训练大量仿真数据得到预训练模型,再训练小样本实测数据,研究表明该方法可有效实现未探测海域的声源距离估计。
对陌生海域,既没有足够的水声数据,也没有环境参数用来产生大量拷贝场数据,无法训练出准确的深度神经网络,而迁移学习可作为学习框架,将已知海域的知识应用到陌生海域的探测中,因此,迁移学习在水声被动定位领域的应用有着较大的研究意义。本文充分利用了已知海域的大量水声数据,训练得到对应的预训练模型,将迁移学习应用在仅有少量水声数据的海域目标测距上,利用SWellEX-96实验无强干扰的S5数据和有强干扰的S59数据验证了2种环境下该方法的可行性。
1 匹配场处理
通过简正波模型以及环境参数,可以计算出声源在特定位置情况下接收阵上的复声压,作为拷贝向量。在简正波模型下,(0,zs)处单频点声源在(r,z)处产生的声压表达式[17]为:
(1)
式中:ρ为介质密度;Ψm(z)和krm分别为第m号简正波的模深函数(特征函数)和水平波数。
对水听器阵列接收到的数据与拷贝向量进行匹配,在计算得到的距离-深度模糊表面中寻找最大值,该点对应位置即为估计位置[18]。由互谱密度矩阵R和拷贝向量ω计算MFP的定位模糊度平面B:
B(φ)=ωH(φ)Rω(φ)
(2)
(3)
ω=[p1,p2,…,pl,…,pL]T,l=1,2,…,L
(4)
式中:ω为拷贝向量;pl为拷贝场下基阵接收到的复声压;φ为声源位置参数;L为快拍数;Pl为第l个快拍下基阵频域数据向量。对宽带信号,累加平均各个频率对应的模糊度平面,即可得到宽带信号的模糊度平面。
2 深度迁移学习与数据预处理
用于水下测距的迁移学习利用从一个场景(模型声场或者历史环境声场)学习到的知识来对新环境的声源进行测距。传统机器学习模型对不同领域的数据集进行独立训练,无法直接应用在其他环境中(如图1所示)。卷积神经网络是深度神经网络中的一种,并已大量应用于水声目标的分类和定位中。迁移学习建立在传统卷积神经网络的基础上,可以将一个预训练模型迁移到一个新的领域中(如图2所示)。本文中,预训练模型由经归一化后的实验水声数据训练得到,并将其迁移到另一个海域仅有小样本水声数据的目标距离估计研究中。
2.1 数据预处理
为了减小声源振幅的影响,L元阵列接收的频域复声压进行范数归一化操作:
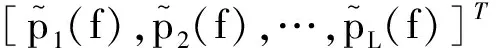
(5)
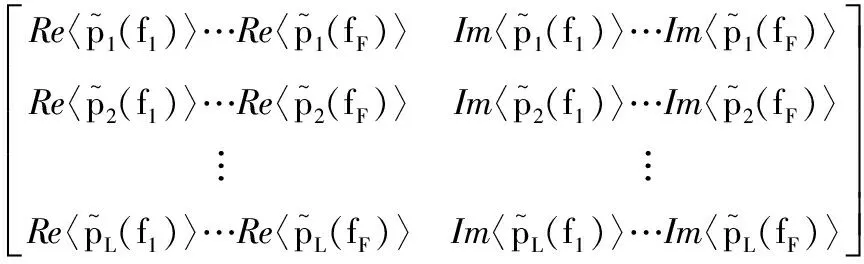
(6)

图1 传统机器学习系统Fig.1 Traditional machine learning system

图2 迁移学习系统Fig.2 Transfer learning system
2.2 衡量标准
为比较不同声源测距方法的定位性能,将平均绝对百分比误差(mean absolute percentage error,MAPE)作为衡量指标,其定义为:
(7)
式中:Rgi为神经网络预测数据;Rti为实际数据。
2.3 神经网络的设计
本文采用CNN的回归模型实现测距,网络包含3个卷积层,3个池化层、全连接层和输出层,各个卷积层后即为一个池化层,3个卷积层中卷积滤波器大小分别为5×5、3×3和3×3,数量分别为128、128和256,3个池化层大小均为2×2,输出采用CNN的回归层,配置训练参数,优化算法设置为sgdm,初始学习率为0.000 1,批训练样本数量为128,如图3所示。

图3 CNN模型Fig.3 CNN model
迁移学习模型可充分利用预选海域的大量水声数据集T1和探测海域的小样本水声数据集T2,对探测海域测试集T3进行目标距离估计,总体流程其搭建和训练如图4所示,具体分为以下步骤:
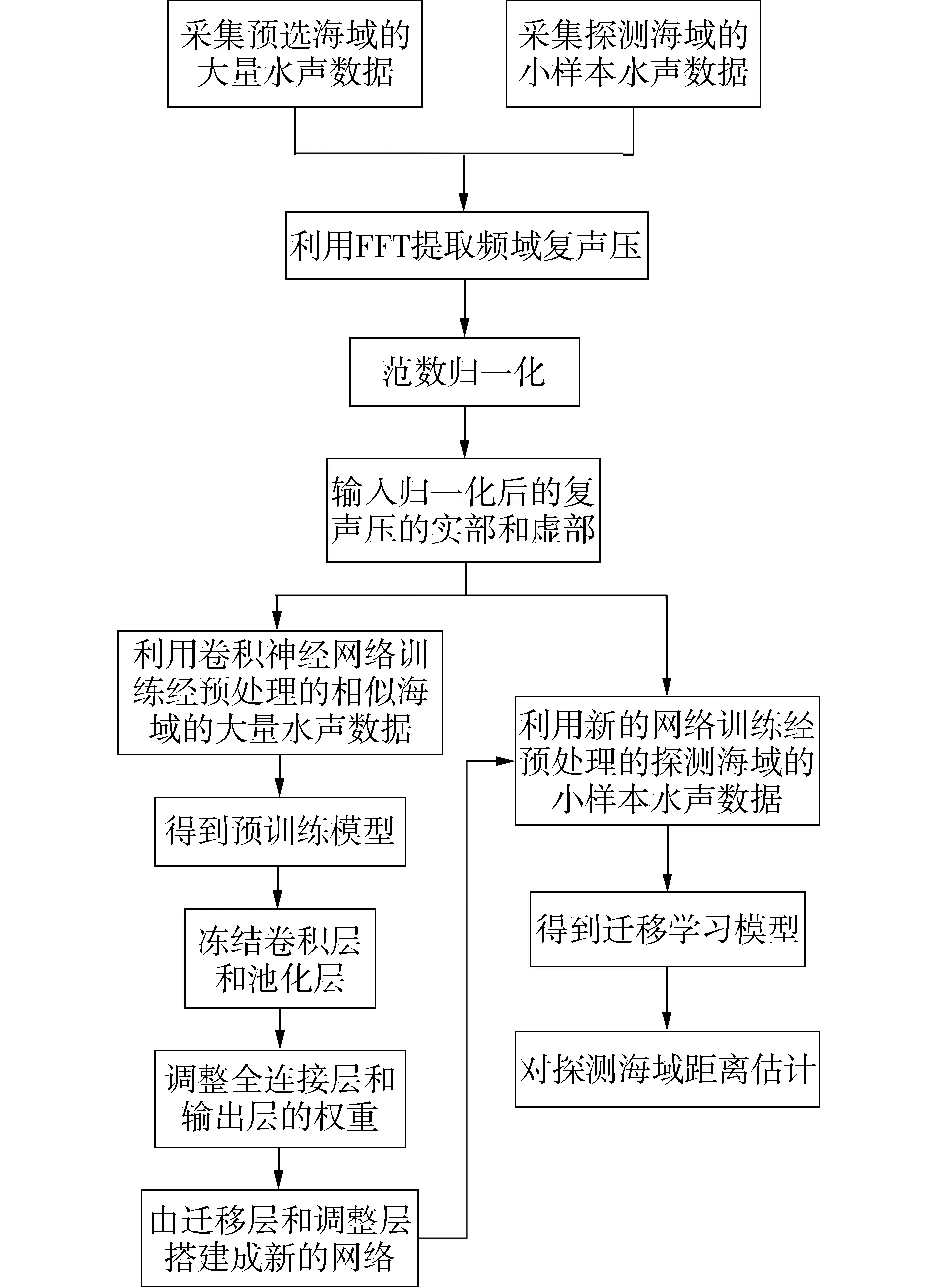
图4 迁移学习方法总体流程框Fig.4 General flow chart of transfer learning method
1)采集预选海域的大量水声数据和探测海域的小样本水声数据,对采集到的时域声压,利用fft提取频域复声压,并进行范数归一化处理;

3)在传统CNN的基础上搭建迁移学习模型,将预训练模型的卷积层和池化层的权重保留,即冻结其卷积层和池化层,作为迁移层;调整全连接层和输出层的权重,作为调整层,并由迁移层和调整层搭建成新的网络;
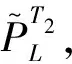
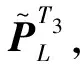
3 海试数据验证
3.1 实验描述
SWellEX-96实验共包含S5和S59这2个航次,图5为海试环境参数,图6为该实验S5和S59航次地图。本文将该实验中S5和S59的垂直阵接收的数据用于网络的训练和测试,分别用于研究无强干扰和有强干扰条件下的距离估计。实验船一共同时拖曳了深(54 m)和浅(9 m)2个声源,2个声源分别发射在49~400 Hz和109~385 Hz多个频点的CW信号,且2个声源发射CW信号的频点不重合,实验船速度约为2.5 m/s,S5和S59航次分别共采集了75 min和65 min数据。在S59实验中,干扰信号由水面舰船发出,频段为62~401 Hz[19]。实验使用共有22个水听器的垂直阵,采样频率为1.5 kHz,布放的深度为94.125~212.25 m,在实验中有一个水听器出现故障,因此仅可使用其他21个水听器的测量数据。
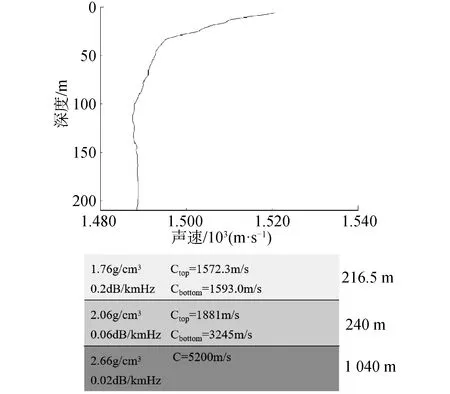
图5 SWellEX-96 实验浅海环境参数模型Fig.5 Swellex-96 experiment shallow sea environment parameter model
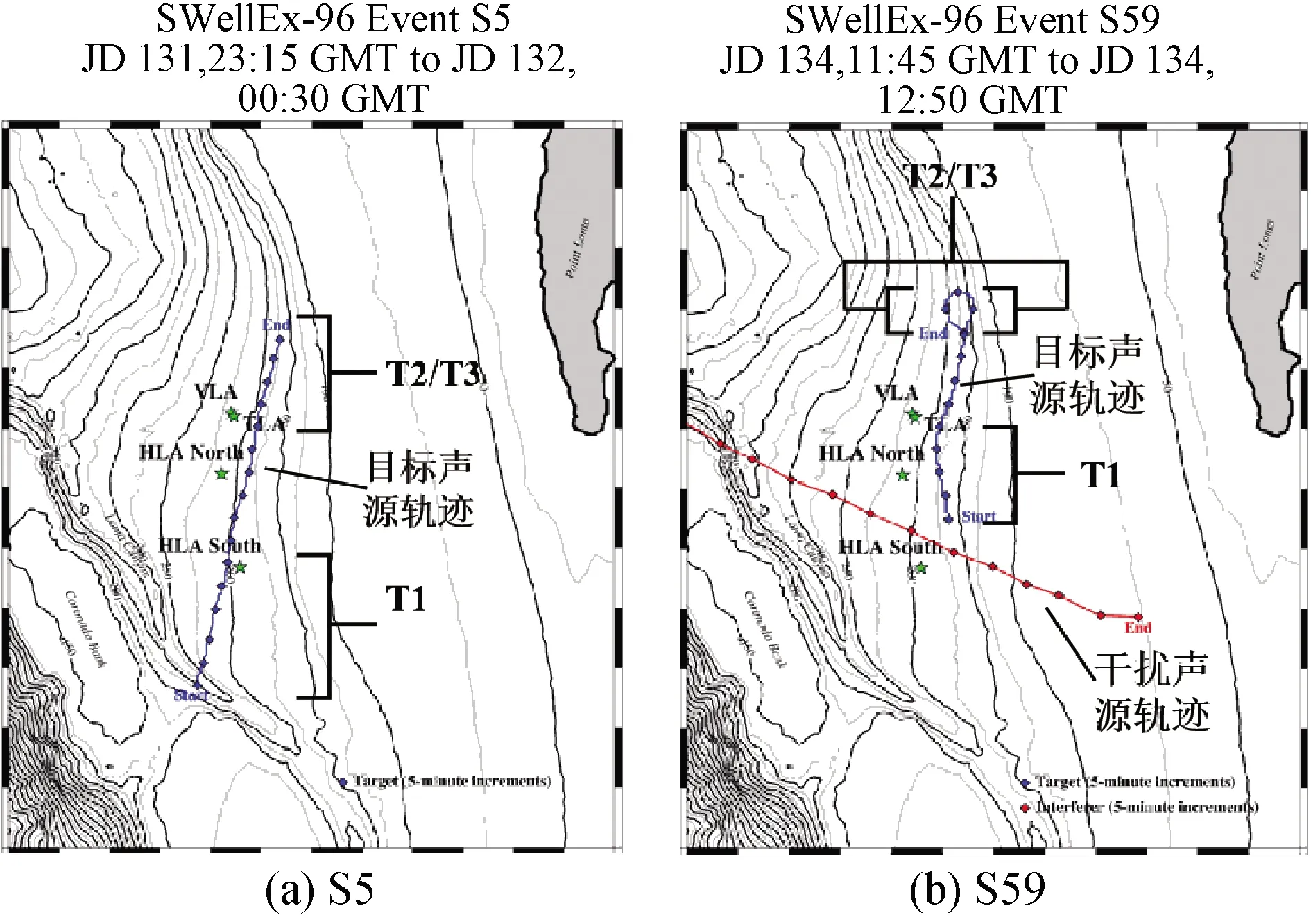
图6 SWellEX-96 实验航次地图及数据集分布图[19]Fig.6 SWellEX-96 experimental voyage map and data set distribution map[19]
3.2 实验数据处理及结果分析
3.2.1 数据集的选取
由于实验中2个声源发射CW信号的频点不重合,所以,本文通过提取不同频点的复声压,可分别对2个声源进行距离估计研究。在SWellEX-96实验中发射声源级最大的一组频点中取得的{109,198,385}和{112,235,388}Hz分别作为浅源和深源的宽带频率。在SWellEX-96实验数据中,选取出T1、T2和T3数据集分别作为预训练数据集、小样本数据集和测试集,各个数据集的分布见图6。
在SWellEX-96实验无强干扰下的S5数据中,实验前30 min中,每1 s提取对应频率的1 s快拍数据,共得到1 800组数据用于预训练,设为T1数据集;实验后15 min中,每5 s提取一组1 s快拍数据作为小样本训练集,共180组数据,设为T2数据集,并在该期间,每19 s提取一组1 s快拍数据作为测试集,共48组数据,设为T3数据集,其中,T1和T2数据集的间距为4.5 km。
在SWellEX-96实验强干扰下的S59数据中,实验前18.75 min中,每1 s提取对应频率的1 s快拍数据,共得到1 125组数据用于预训练,设为T1数据集;实验后18 min中,每8 s提取一组1 s快拍数据作为小样本训练集,共207组数据,设为T2数据集,并在该期间,每19 s提取一组数据作为测试集(为避免测试集泄露,去除其中与小样本数据集重合的样本点),共76组数据,设为T3数据集,其中,T1和T2数据集的间距为4.2 km。
3.2.2 匹配场处理
设置海域的搜素距离范围是0~5 km,间隔为10 m;深度范围1~200 m,间隔为1 m,利用上述参数计算拷贝场。测试海域为浅海,且为距离不相关的波导环境,声源发射信号为低频,因此使用基于简正波模型的Kraken程序进行仿真。声压场的互谱密度矩阵由S5实验T3数据集中3个1 s的快拍数据计算得到,基于Bartlett算法估计出水下目标声源的空间位置,图7为无强干扰下匹配场处理方法下的距离估计结果。可知在无强干扰下,由于简正波模型在距离为0~2 km的条件下不适用,该部分测试集的估计准确度较低,而其他测试集的估计性能较好,但仍有一定的误差,相对深源,浅源的估计结果较好。
对于强干扰下的S59数据,拷贝场数据同上,声压场的互谱密度矩阵由S59实验T3数据集中3个1 s的快拍数据计算得到,图8为强干扰下匹配场处理方法下的距离估计结果,可得到,因为基于模型驱动的MFP方法严重依赖环境参数,拷贝场已与强干扰下的实际环境相差过大,导致MFP方法已不适用。
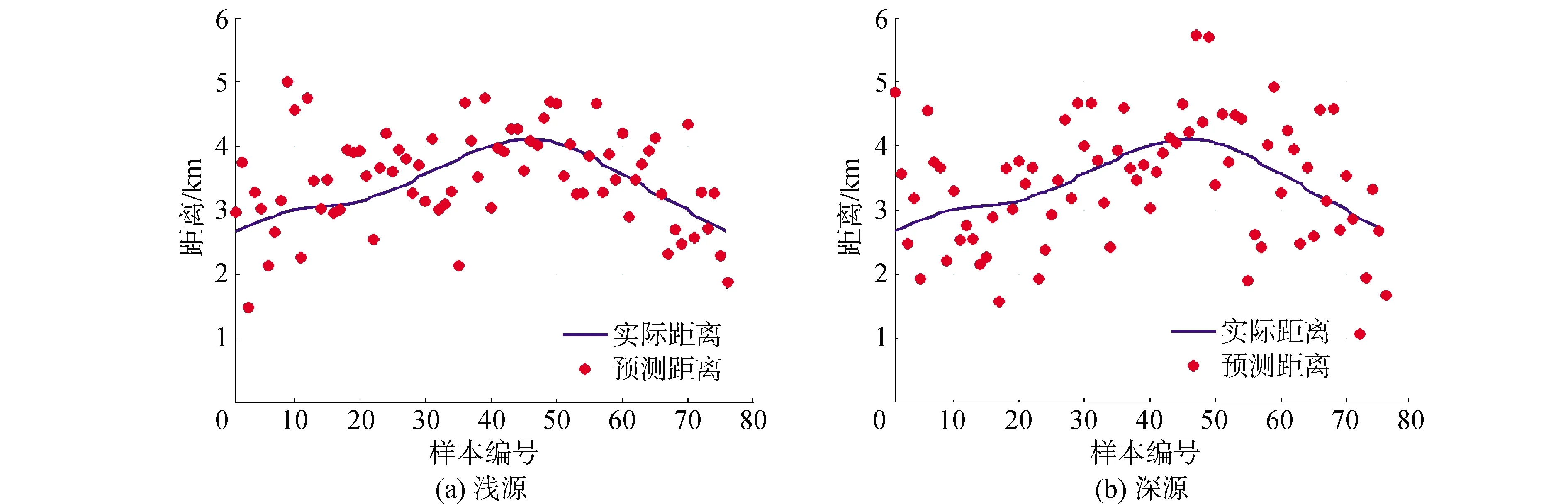
图8 强干扰下MFP方法的距离估计结果Fig.8 Distance estimation of MFP method with strong interference
3.2.3 传统卷积神经网络
在研究无强干扰下S5数据的小样本场景中,利用传统CNN方法训练,当训练集分别为T1数据集、T2数据集和T1/T2数据集时,图9、10和11分别为无强干扰下3种训练集下T3数据集的估计结果,可得到,在无强干扰的环境中,训练集为T1时,由于训练集与测试集距离相差较大,神经网络模型不易对测试集进行预测,所以,该场景无法实现有效距离估计;训练集为T2时,由于训练集和测试集均在同一片海域,所以,可在一定程度上实现距离估计,但受限于训练集数据量较小,误差仍较大;训练集为T1和T2的混合数据集时,因为混合数据集不仅数据量较大,而且包含和测试集同一海域的T2数据集,所以可以较好地实现距离估计,但仍有一定的误差。

图9 无强干扰下训练集T1传统CNN估计结果Fig.9 The traditional CNN estimation results of T1 training set without strong interference
在研究强干扰下S59数据的小样本场景中,网络结构和无强干扰下的一致,经传统卷积神经网络训练,图12~14分别为强干扰下3种训练集的T3数据集距离估计结果。可知,传统卷积神经网络在强干扰和小样本场景中,由于强干扰下,训练集和测试集差别较大,训练得到的CNN模型无法对测试集实现有效预测,导致3种训练集下均无法得到准确的距离估计结果。
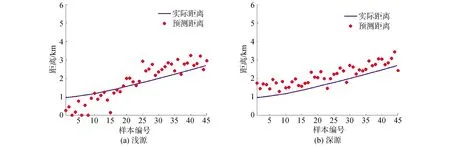
图10 无强干扰下训练集T2传统CNN估计结果Fig.10 The traditional CNN estimation results of T2 training set without strong interference

图11 无强干扰下T1和T2混合训练集传统CNN估计结果Fig.11 The traditional CNN estimation results of T1 and T2 hybrid training set without strong interference
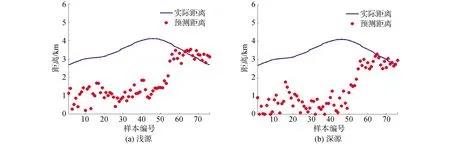
图12 强干扰下T1训练集下传统CNN估计结果Fig.12 The traditional CNN estimation results of T1 training set with strong interference
3.2.4 迁移学习
在研究无强干扰下S5数据的小样本场景中,经迁移学习模型训练,图15为其距离估计结果,可得到,在无强干扰下,通过迁移学习方法,对浅源和深源均可以实现有效地距离估计。对于强干扰下S59数据的小样本场景,迁移学习网络结构和无强干扰下的一致,图16为强干扰下迁移学习模型距离估计结果。可知,相比MFP和传统CNN方法,迁移学习可较为准确地实现目标距离估计,但由于存在运动中的干扰源,相比无强干扰环境,强干扰下深源和浅源的距离估计结果均较差。
表1和表2分别列出了无强干扰和强干扰下各个方法距离估计结果的MAPE。由横向对比可得,浅源和深源在迁移学习下的MAPE均远小于传统CNN和MFP,迁移学习的估计性能明显优于传统CNN和MFP;相比训练集为T1,训练集为T2数据集的传统CNN估计性能较好,由此可见,训练集和测试集位置相差较小时,估计性能较好,若T2数据集样本数较多,传统CNN理论上也可对测试集得到较准确的距离估计结果,但在小样本场景中,通过传统CNN无法实现有效距离估计;由于相比训练集仅为T1或T2,训练集为T1/T2的传统CNN方法数据量较大,从而可以更充分地训练,所以,在各种训练集的传统CNN方法中其估计性能最好;训练集为T1/T2的传统CNN方法和迁移学习方法用于训练的数据量一致,但前者是在大范围地训练和估计,而后者是在已经训练出的相近模型权重的条件下,对小样本海域再训练,即在充分利用了相近海域水声数据的基础上,对包含测试集的小样本海域实现小范围地重点训练和精确估计,所以,相比训练集为T1/T2的传统CNN方法,迁移学习方法估计结果较好。由纵向对比可得,相比深源,浅源的估计性能普遍较好,这是某些时间深源的信号缺失造成的,见图17中椭圆标注,S5和S59数据中深源的信号分别以388 Hz和235 Hz为例,椭圆区域均有不同程度的信号缺失,而实验中浅源的信号较为完整。
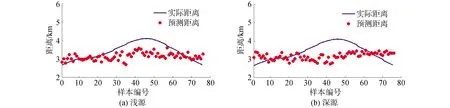
图13 强干扰下T2训练集下传统CNN估计结果Fig.13 The traditional CNN estimation results of T2 training set with strong interference
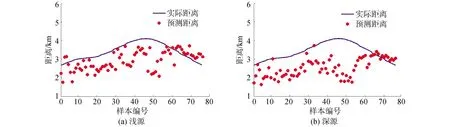
图14 强干扰下T1和T2混合训练集下传统CNN估计结果Fig.14 The traditional CNN estimation results of T1 and T2 hybrid training set with strong interference

图15 无强干扰下迁移学习模型距离估计结果Fig.15 Transfer learning model estimation results without strong interference
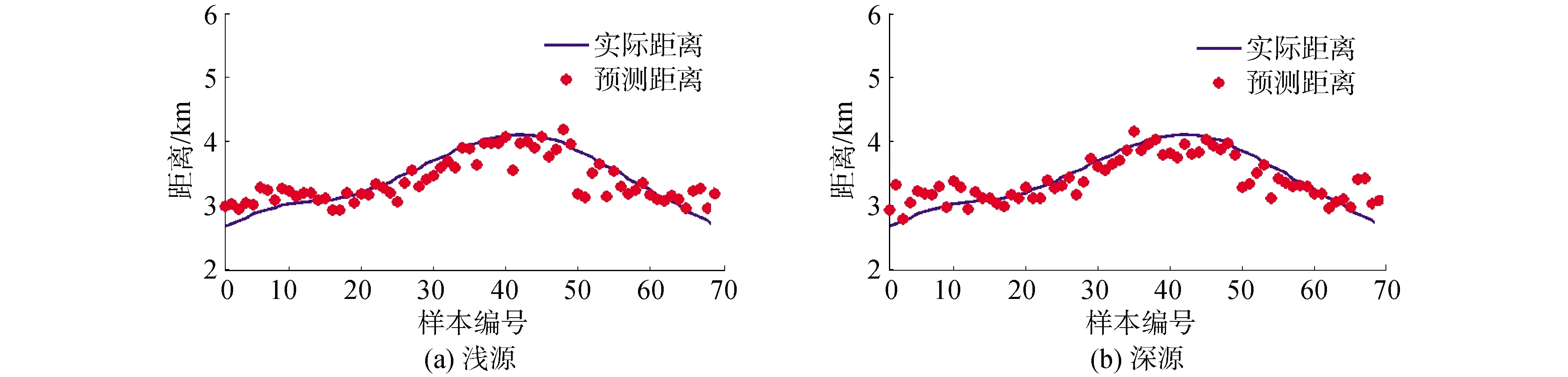
图16 强干扰下迁移学习模型距离估计结果Fig.16 Transfer learning model estimation results with strong interference

表1 无强干扰下浅源和深源在不同方法下距离估计结果的MAPE
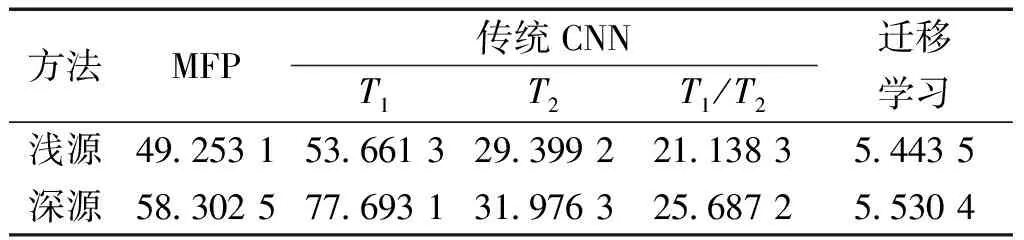
表2 强干扰下浅源和深源在不同方法下距离估计结果的MAPE
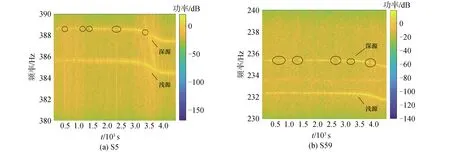
图17 SWellEX-96 实验声源功率谱图Fig.17 Sound source power spectrum diagram of SWellEX-96 experimental
4 结论
1)机器学习在水声被动定位领域的结合日益密切,在仅有探测海域的小样本水声数据时,迁移学习可以作为学习框架,将已有的知识应用到新的环境中,减少了探测海域所需的训练集数据量。
2)本文提出了基于卷积神经网络的迁移学习模型,并利用SWellEX-96实验无强干扰的S5航次数据和有强干扰的S59航次数据进行了方法的验证,对比了MFP、传统CNN和迁移学习3种方法的水下目标距离估计性能。实验数据处理结果表明,在无强干扰和小样本场景下,MFP方法在距离为0~2 km的环境中不适用,传统CNN方法仅在训练集为T1/T2时有着较好的定位,而迁移学习方法可以实现稳健的距离估计,在强干扰和小样本场景下,MFP和传统CNN方法均已不适用,而迁移学习方法可以得到有效准确的距离估计。
3)迁移学习模型在水声被动定位领域的研究较少,有着较大的研究空间,不同类型的干扰、测试集与训练集深度不同等场景下的目标距离估计,有待进一步的探索。

