利用声压幅值相关性识别声源特性研究

潘邦雄，罗瀚波，赵秀亮，赵晓丹

（江苏大学汽车与交通工程学院，江苏镇江 212013）

声源识别可以从声学系统中得到声源位置，能量分布，频率特性等信息，是噪声控制工程的重要组成部分，在机械设备故障检测中有广泛应用[1]。波束形成是一种目前主要使用的声源识别技术[2]，延时求和是一种经典的波束形成算法[3-4]，它可以有效地识别平面波入射方向。随着发展，波束形成方法逐步拓展到球面波声源识别[5-6]、表面噪声源识别与排序[7]、风扇空气动力噪声源识别等[8]，并由固定点声源识别进化到运动点声源识别[9-10]。为了提高波束形成的识别效果，国内外学者在延时求和算法的基础上做出改进，提出了MUSⅠC 声源定位[11-12]、互功率谱波束形成[13-14]和除自谱的互功率谱波束形成等算法[15-16]，以上这些算法虽然在操作形式上与延时求和有所不同，但都仍然以相位信息为核心进行声源识别，识别过程中传声器阵列需要进行严格的相位匹配，对测量仪器要求很高。

本文将延时求和算法的输出结果转化成内积运算的形式，然后提出利用声压幅值信息通过内积运算来对声源进行识别。以球面波为例，分析推导用声压幅值信息进行声源识别的方法，继而建立具体的声源识别步骤，对辐射简谐波的声源进行识别并与波束形成法的识别特性相比较，最后结合仿真计算与消声室实验对该方法进行验证。

1 延时求和波束形成算法内积形式推导

延时求和算法通过对各传声器接收到的声压信号进行相位匹配与累加求和来识别声源入射方向，图1 为平面波模型下的延时求和算法示意图，根据波束形成理论[17]，该方法的输出为：

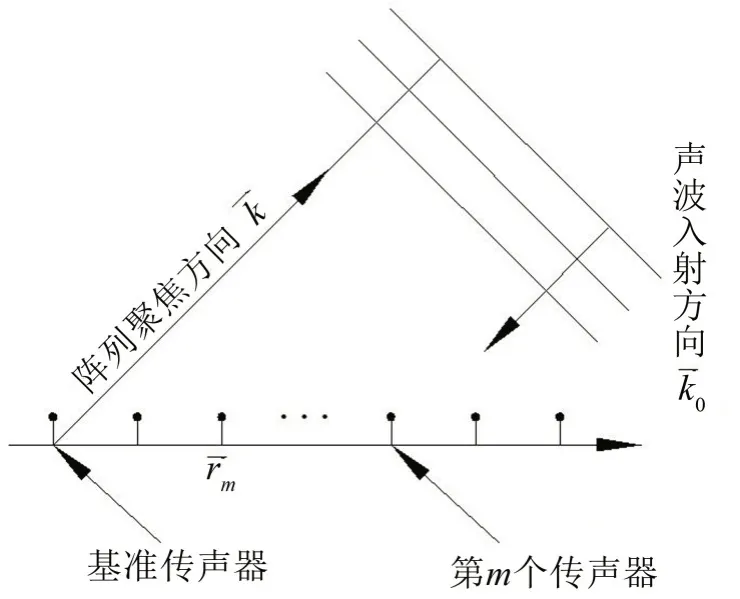
图1 波束形成方法示意图

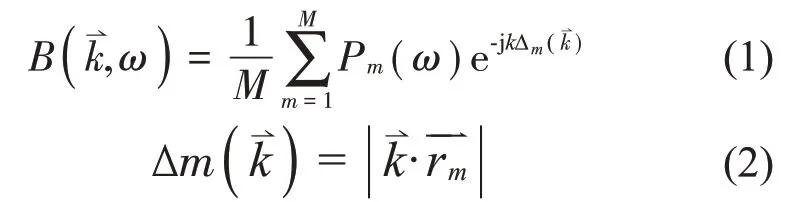
其中：B（,ω）是阵列聚焦方向为k⇀，声源角频率为ω时，波束形成方法的总输出；M表示阵列中的传声器个数；Pm（ω）表示第m个传声器所接收到的声压信号；为波数；c为声速表示阵列聚焦方向表示基准传声器到第m个传声器的距离；是向量在向量方向上的投影，即声波到基准传声器与到第m个传声器的声程差。

将每个传声器接收到的信号相对参考传声器进行时延，然后求和，当阵列聚焦到声波入射方向时，各个传声器接收到的声压信号相位相同，该方向上入射的信号因为同相而增强，总输出B（,ω）在方向上取到最大值，从而判定声源入射角度。

对输出结果B（,ω）做形式上的转换，各传声器接收的声压信号Pm（ω）可以表示为：

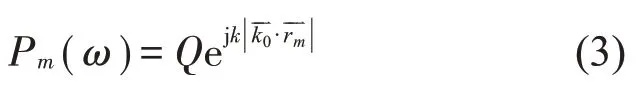
其中：Q表示基准传声器接收到的声压信号值；表示入射方向为的声波到基准传声器与到第m个传声器的声程差。将各个传声器接收到的声信号Pm（ω）整合成M维声压向量：

将聚焦方向对应的延时量整合成M维时延向量b：

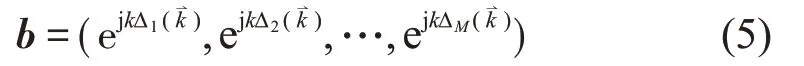
输出结果B（,ω）可以表示为：

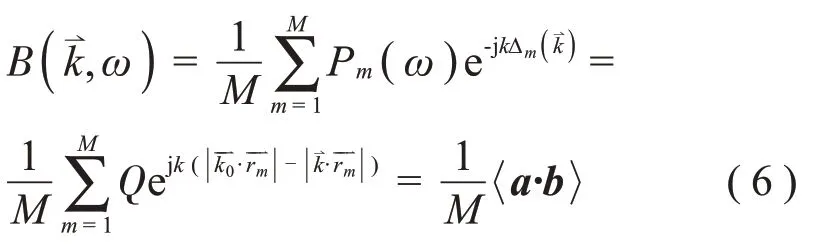
其中：a·b表示向量a与向量b的内积。

由以上转换可知，延时求和波束形成算法本质上是一种通过内积运算进行的相关诊断，当阵列聚焦方向与声波入射方向一致时，声压向量a与时延向量b达到同一相位，两者构成相关关系，两个向量之间的内积取到最大值，由此判断出声波入射方向。

2 算法理论分析与识别步骤

前面分析，延时求和波束形成算法是通过求声信号相位信息的最大相关性来进行声源识别的。实际上，传声器阵列接收的声压信号中，除了相位信息以外还包括其他信息，比如声压幅值信息。课题组前期针对声压有效值进行白噪声声源识别进行了探究，本文进一步尝试利用声压幅值信息做相关运算来识别简谐波声源。

球面波声源具有典型性，工程实践中常常将复杂声源简化成一个或多个球面波声源[18]，以其为例进行分析。假设在阵列面的上方空间内存在一个球面波声源S，示意图见图2，球面波声源S的声压辐射公式p（t）是：

图2 利用声压幅值进行声源识别示意图

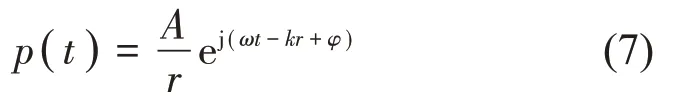
其中：A反映声源强度；r为接收点到声源的距离；φ为声源初相位。

假设使用一组M×N维的传声器阵列进行测量，位于阵列第i行第j列的传声器Mij（i=1,…,M;j=1,…,N）测得的声压信号幅值pij为：

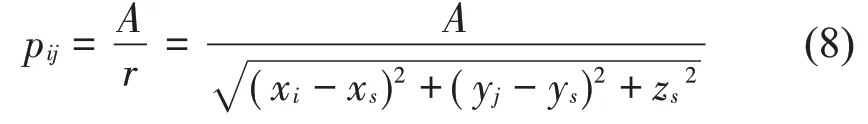
其中：（xs,ys,zs）表示声源的空间位置；（xi,yj,0 ）表示传声器Mij在XOY平面上的坐标。

将每个传声器测得的声压幅值按其在阵列中的位置整合成M×N维的声压幅值向量：

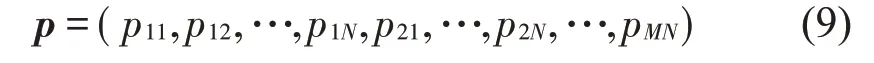
在声源可能存在的空间区域内设置虚拟声源S'，强度为1Pa·m，利用公式（7）计算虚拟声源辐射到传声器Mij处的声压幅值p'ij：

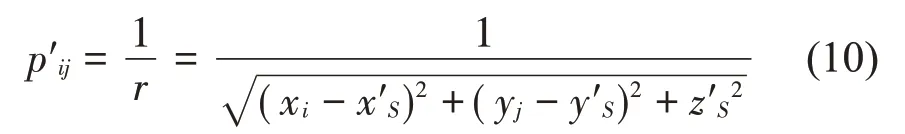
其中：（x′S,y′S,z′S）表示虚拟声源的空间位置，同样将p′ij整合成虚拟声压幅值向量：

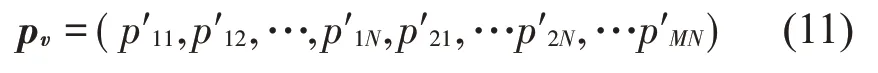
向量pv进行归一化运算得到归一化向量e：

将向量p与向量e做内积运算并取模值，根据柯西-施瓦兹不等式定理[19]：向量p与向量e的内积模值小于等于这两个向量各自模的乘积：

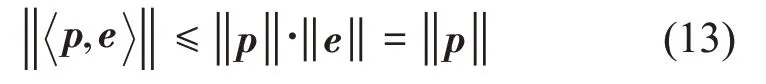
当且仅当两个向量满足如下关系时：

其中：q为常数，向量e与向量p成线性相关关系，式（13）中的等号成立，内积模取到最大值由公式（14）可知，此时虚拟声源的位置与目标声源重合，即x′S=x′S,y′S=ys,z′S=zs。以上理论分析表明，通过搜索的最大值，使用声压幅值信息进行相关运算即能识别声源。识别出声源位置时，向量p与向量pv有以下关系：

作向量p与向量e的内积：

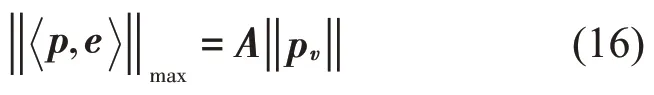
可得声源强度：

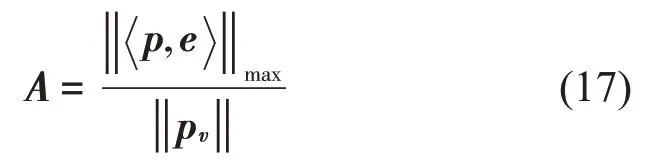
基于以上理论分析进行声源识别，建立识别步骤如下：

步骤（1）使用传声器阵列进行测量，得到阵列中各传声器处的声压幅值pij，按公式（9）组成声压幅值向量p；

步骤（2）在声源可能存在的区域内先划分粗略的网格，在网格的节点上设置声源强度为1 Pa·m的虚拟球面声源S′；

步骤（3）用公式（10）计算虚拟声源辐射到各传声器的声压信号幅值p′ij，按公式（11）组成虚拟声压幅值向量pv；

步骤（4）向量pv进行归一化运算得到向量e，计算向量p与向量e的内积模值；

步骤（5）虚拟声源在网格上遍历，重复步骤（3）～步骤（4）得到各网格点的内积模值；

步骤（6）搜索内积模值的最大值，找到最大值对应的网格点位置；

步骤（7）采用逐级细化在最大值位置附近做更密集的网格划分，重复步骤（2）～步骤（6）做进一步的细化搜索；

步骤（8）判断精度是否满足要求，未达到精度要求时返回步骤（7），达到精度要求时停止搜索，得到声源位置。

步骤（9）根据公式（17）计算出声源强度。

3 简谐波声源识别结果对比

3.1 识别平面上的点声源

仿真算例1：设声源面距离测量面0.5 m，声源理论位置为（0.451 3 m，0.322 2 m），声源强度0.707 Pa·m，声源频率200 Hz。传声器阵列维数为6×6，传声器间距为0.3 m×0.3 m，要求声源识别精度为0.001 m。分别使用延时求和波束形成方法与本文方法对该简谐波声源进行识别。两种方法的识别结果如表1所示，输出分布如图3所示。

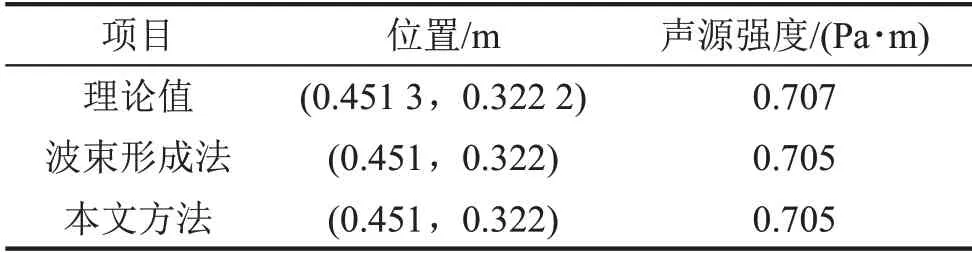
表1 平面上点声源识别结果

从表1和图3可以看出，两种方法的输出结果在声源面上的分布都存在唯一一个最大值与声源位置对应，且两种方法识别出的声源强度与理论值也基本符合，证明两种方法均能准确识别出声源位置。但是，波束形成法计算声源强度的过程需要考虑各传声器接收到声压信号幅值的差异性，引入互谱函数算法，计算过程相对复杂[20]。而本文方法利用公式（17）进行运算可以得到准确的声源强度，计算过程更简便。

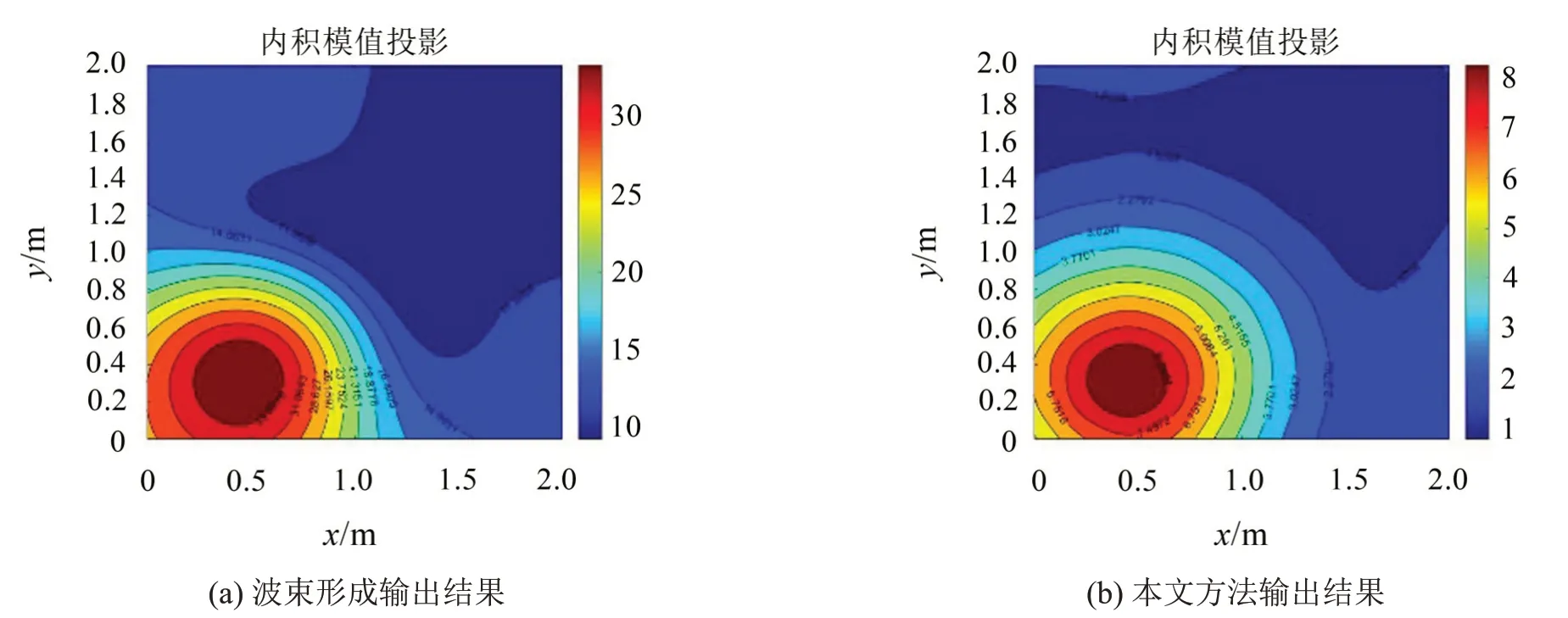
图3 两种方法的输出分布

3.2 识别空间中的点声源

仿真算例2：设声源位于1 m×1 m×1 m的空间区域内（如图2），传声器阵列与识别区域下表面之间的距离是0.2 m，声源理论位置为0.535 6 m，0.468 5 m，0.735 4 m，声源强度0.707 Pa·m，频率200 Hz，要求声源识别精度为0.001 m。

同时，为了考察本文方法的抗噪能力，在仿真算例2 的声压信号中加入高斯白噪声信号，观察在信噪比分别为20 dB，15 dB，10 dB下的识别效果，结果如表2所示。

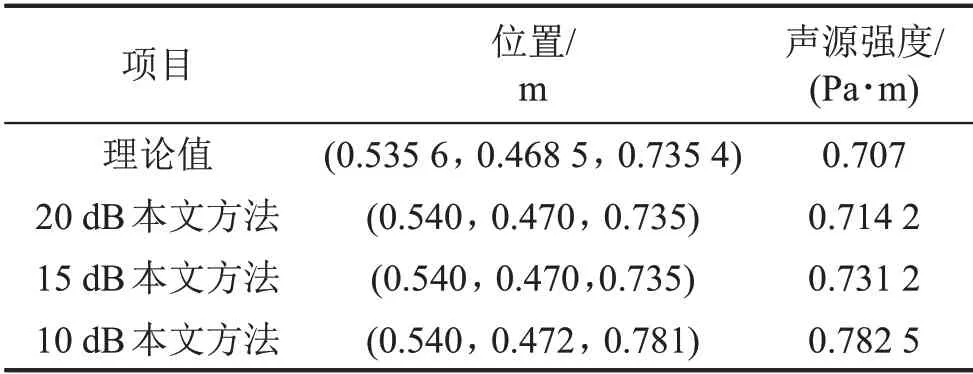
表2 空间上点声源识别结果

由表2可知，在不同强度的随机噪声干扰下，本文方法对声源位置的识别结果基本稳定，当信噪比在15 dB 以上时，识别值与理论值的偏差低于5%，在工程测量允许的误差范围以内。这是由于本文方法使用的内积运算具有一定的滤波作用，能够较好地减弱随机噪声的干扰。而延时求和等传统波束形成算法可以识别二维平面上的声源，但在识别声源深度方面计算过程复杂，搜索效率低下[21—24]。本文方法对三维空间中声源的识别只比二维平面多一维搜索，无需调整传声器阵列形状，计算简便，识别速度更快。

3.3 声源频率对识别效果的影响

仿真算例3：使声源辐射200 Hz 和4 000 Hz 的简谐波，其余参数的设定与仿真算例1 中相同。分别使用两种算法对声源进行识别，识别结果如表3所示，两种方法在声源面上的输出分布如图4所示。

表3 不同频率下两种方法的识别结果

从图4中可以看出，识别低频声源时，以上两种方法的输出都只存在唯一的峰值与声源位置对应；识别高频声源时，波束形成方法在声源位置外也出现了输出峰值，这是由于传声器间距大于声源所辐射声波波长而导致的“鬼影”现象，而本文方法仍然只存在唯一一个峰值与之对应。这说明本文方法识别高频声源时，能有效避免“鬼影”现象的产生，从而提高了声源位置的识别精度。

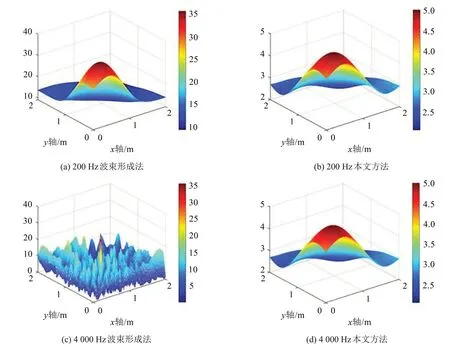
图4 不同频率下两种方法的输出分布

3.4 传声器阵列安装误差对识别效果的影响

仿真算例4：假设简谐波辐射的点声源强度0.65 Pa·m，频率1 000 Hz，声源位置为（0.256 4 m，0.856 7 m）。传声器阵列设为6×6的矩形阵列，间隔为0.2 m×0.2 m，声源深度为1 m。阵列中第i行第j列传声器的实际位置为（xij±εx,yij±εy,zij±εz），其中εx,εy,εz表示传声器在XYZ方向上的位置偏差，均满足μ=0.01m,σ=0.005 m的正态分布，分别使用本文方法与波束形成方法识别，结果如表4所示。

从表4 可以看出，在传声器实际位置与标量之间存在一定误差的情况下，本文方法识别出的声源位置与强度信息误差均小于1%，准确识别出了声源，而波束形成方法在考虑传声器位置偏差时的识别误差大于5%，这是由于使用以相位信息为核心的声源识别方法进行识别时，传声器位置的偏差对相位的影响较大（尤其是在识别高频声源时），而本文方法使用声压信号有效值为信息基础进行声源的识别，传声器位置偏差带来的声源强度误差较小，在一定传声器位置误差下仍然能保持较好的识别效果。

表4 传声器位置误差影响的结果

4 实验验证

在半消声室内进行实验，图5 展示了实验装置的现场图，球声源用铰链悬吊在空中，球声源球心与阵列之间的距离为1 m，球声源在声源面的坐标是0.15 m，0.32 m。使用YG201 型传声器组成的4×8通道阵列进行测量，传声器间距为0.1 m×0.1 m。控制OS003 型无指向型球声源分别产生300 Hz 和3 000 Hz 的简谐声波，声源强度为0.127 3 Pa·m，使用UT3408FR3-ⅠCP 型信号采集系统采集各测量点处声压信号，采样频率为12 800 Hz，采样时间2.58 s，分别使用波束形成方法与本文方法进行识别。观察距离阵列1 m平面上的波束形成输出与内积模值分布情况如图6 所示，声源识别实验结果如表5所示。

图5 实验现场照片

从图6 的声学成像可看出，在声源存在的区域两种方法的输出分布均存在峰值与声源位置对应，声源频率的改变对内积模值的分布几乎没有影响，但对波束形成的输出分布影响较大，当声源频率达到3 000 Hz时，在没有声源存在的位置也出现了“鬼影”。由表5的识别结果可看出，两种方法对不同频率声源的识别结果稳定，识别误差均小于0.05 m，在工程测量可接受的范围之内。证明本文方法能有效识别空间中的简谐波声源，并有效避免了传统波束形成方法识别高频声源时出现的“鬼影”现象。

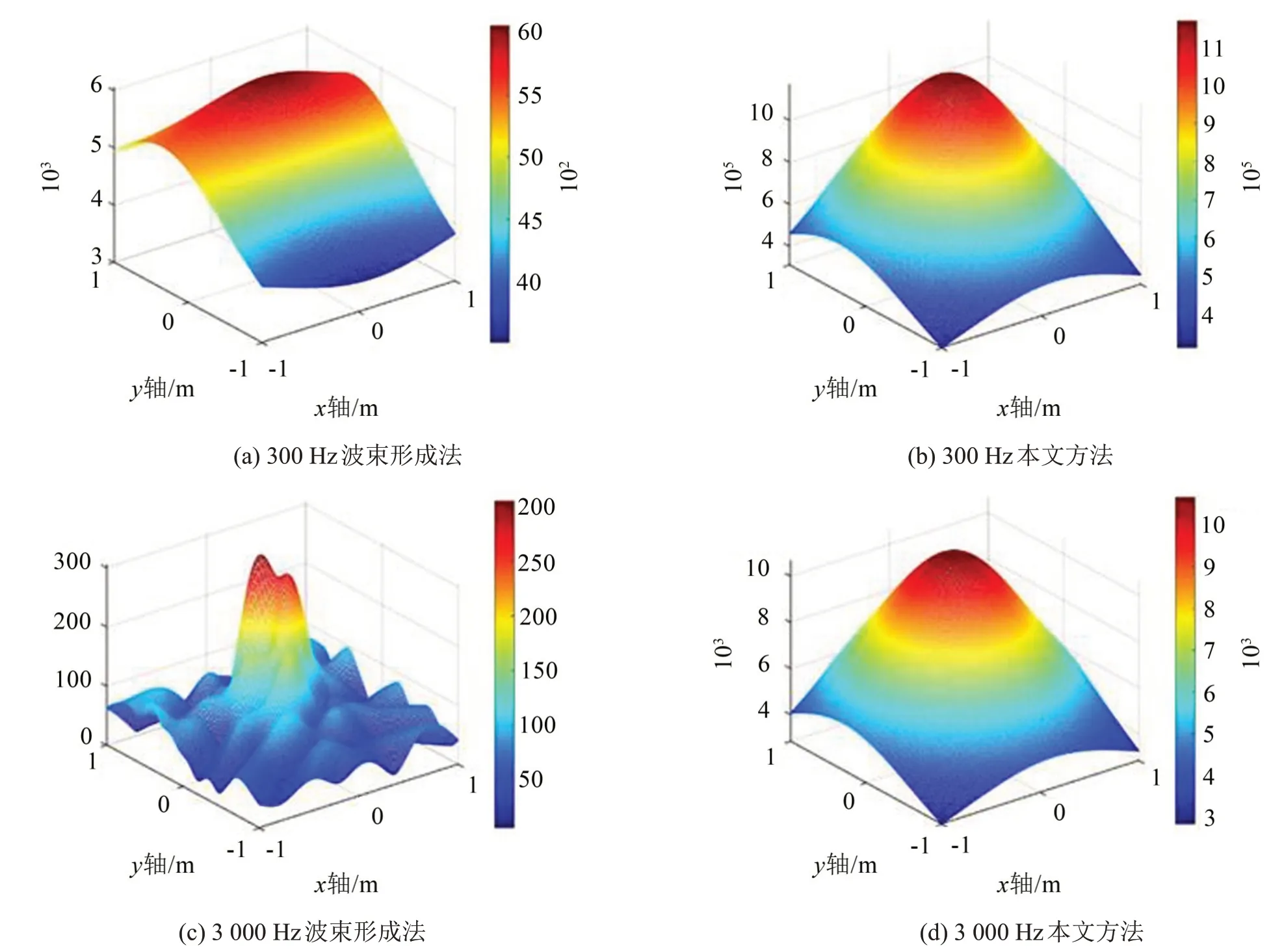
图6 不同频率下两种方法输出分布

表5 不同频率下两种方法识别结果

5 结语

（1）本文提出一种利用声压幅值信息进行声源识别的方法，该方法通过测量声压信号的幅值，组成声压幅值向量，将声压幅值向量与虚拟声压幅值向量作内积，进行相关运算来识别声源。

（2）利用该方法对简谐波声源进行识别并分析其抗噪能力，将识别结果与延时求和波束形成的识别结果作比较。结果表明，该方法能准确识别出声源位置。相比于传统波束形成算法，该方法无需对传声器阵列进行严格的相位匹配；同时，消除了传统波束形成算法识别高频声源时产生的“鬼影”现象，提高了识别精度。

（3）本文方法在传声器阵列存在安装误差时，比波束形成法拥有更准确的识别效果，具有一定的工程实用性。