空频块编码正交频分复用水声通信中的超前正交匹配追踪稀疏信道估计
郭丽华
(哈尔滨学院 黑龙江省地下工程技术重点实验室,黑龙江 哈尔滨 150086)
正交频分复用(orthogonal frequency division multiplexing,OFDM)调制解调技术近年来在无线和水声通信领域取得了广泛的应用,这主要得益于:1)循环前缀可以抗多途信道的频率选择性衰落;2)基于傅里叶变换的调制解调技术使其在硬件平台上可以有效地实现[1-2]。随后的发展多入多出(multiple-input multiple-output,MIMO)技术可以进一步拓展无线通信系统的系统容量以及稳健性;在恶劣的水声环境下,为了提高水声OFDM系统的通信性能,人们将陆地无线通信系统中的空时块编码(space-time block coding,STBC)技术应用到了水声通信领域中[3-8]。然而,实际的仿真和试验结果表明,水声OFDM系统的空时相干性不足以满足空时块编码技术在水声信道上的应用,研究发现水声OFDM系统在频率上具有较好的相干性,因此,利用水声OFDM系统在频率上的相干性,开展了基于空频块编码(space-frequency block coding,SFBC)技术的水声OFDM技术的研究,实际的试验数据处理结果也验证了基于空频块编码技术的水声OFDM系统的性能优于空时编码技术的水声OFDM系统的性能[4-5]。
在空频块编码OFDM水声通信系统中,水声信道估计的精度决定了水声通信系统的性能;文献[5]中提出了一种基于自适应门限的最小二乘稀疏水声信道估计技术,试验数据处理结果表明该算法能够以较低的复杂度实现接近基于正交匹配追踪(orthogonal matching pursuit,OMP)稀疏信道估计技术的性能[9-13]。本文提出了一个低复杂度的超前OMP(look-ahead OMP,LAOMP)稀疏信道估计算法,并将该算法应用于SFBC-OFDM水声通信系统中。
1 SFBC OFDM系统模型
1.1 空频块编码发射系统模型
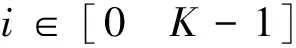
(1)
图1给出了卷积码编码的SFBC-OFDM系统的发射机结构,其中[5]:
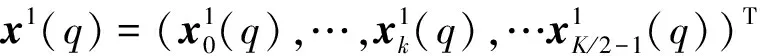
(2)
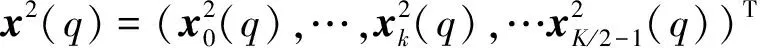
(3)
空频块编码后的符号向量x1(q)和x2(q)经过OFDM调制后可以通过发射换能器1和2分别进行发射。

图1 空频块编码OFDM系统发射机结构Fig.1 Block diagram of OFDM transmitter with space-frequency block coding
1.2 水声信道模型
对于水声OFDM通信系统来说,通常假设信道为块慢变的,在某些实际应用场景中(如移动通信),信道可能是快变的信道,但是可以采用某些预处理过程使得快变信道成为块慢变信道,预处理技术可以通过块多普勒估计与补偿技术对接收信号进行粗的多普勒补偿,进而使得补偿后的信号满足块慢变的假设条件,因此,在块慢变假设下,第m个发射换能器和第n个接收水听器之间的信道模型可表示为[5]:
(4)
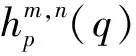
(5)
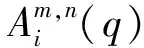
(6)

1.3 空频块编码接收机模型
图2为空频块编码接收机模型。
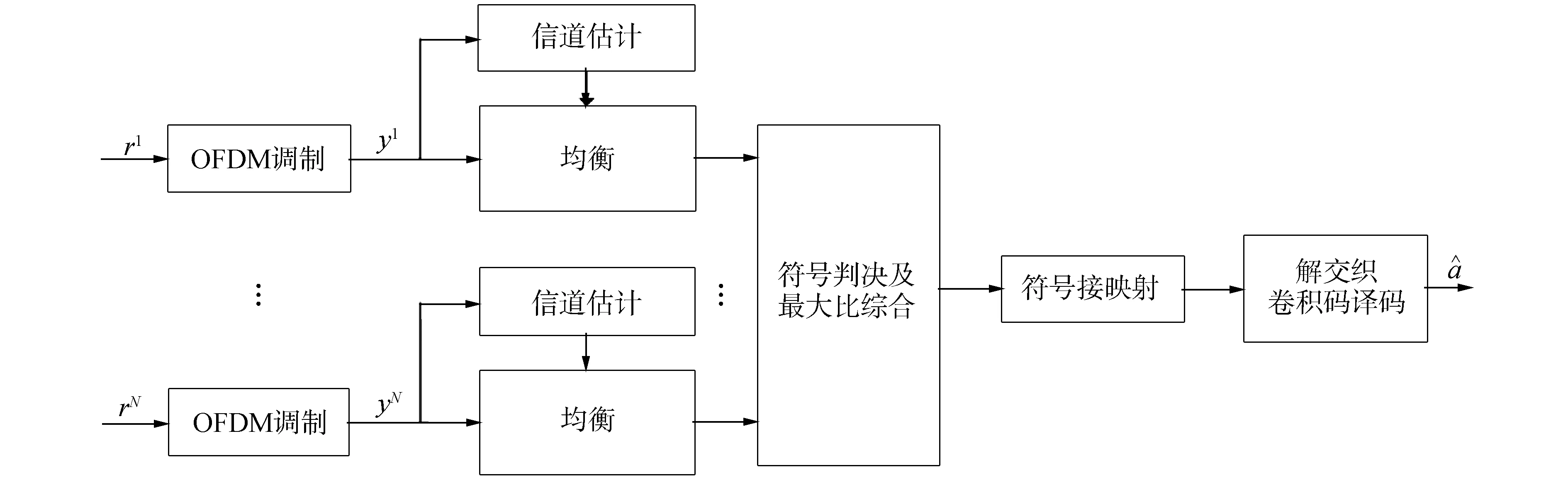
图2 空频块编码OFDM系统接收机结构Fig.2 Block diagram of OFDM receiver with space-frequency block coding
在空频块编码条件下,第n个接收水听器接收到的信号可以表示为[2,5]:
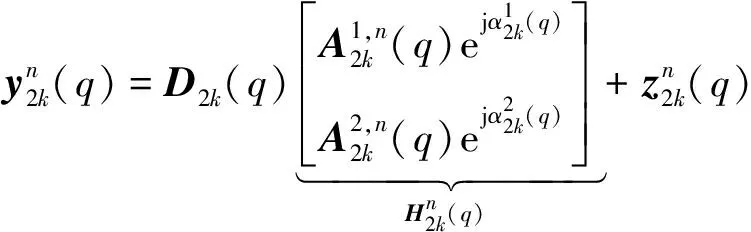
(7)
其中:
(8)
且
(9)
(10)
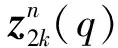
如果发射符号为单位幅度的PSK符号,那么:
(11)
如果发射符号对接收机已知,则可以用最小二乘算法得到信道的估计,即:
(12)
即:
(13)
为了对接收信号进行检测,接收信号模型可以改写成[2,5]:
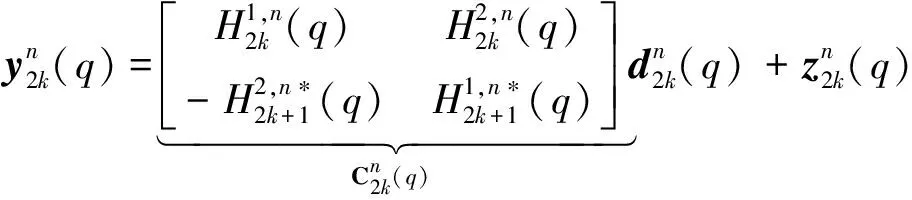
(14)
其中:
如果使用N个接收基元,它们的信号可用向量标识,系统的整体就可以表示为[2,5]:
(15)
基于这个模型,基于最小二乘准则可以得到发射数据的估计:
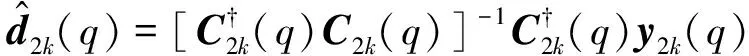
(16)
应用于SFBC的Alamouti假设规定相邻2个载波之间信道不变,即:
(17)
当上述假设成立时,信道矩阵满足性质:
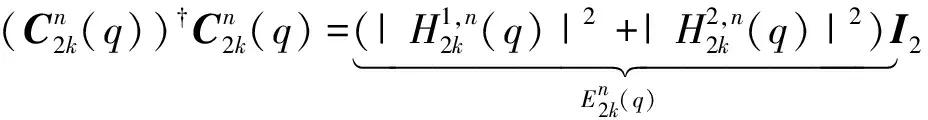
(18)
其中,I2是2×2单位矩阵,最小二乘(least squares,LS)数据估计式(16)可简化为[2,5]:
(19)
1.4 低复杂度超前OMP稀疏信道估计技术
根据式(12)可以得到信道的冲击响应(即做逆傅里叶变换):
(20)
式(20)等价于:
(21)
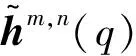
(22)
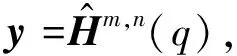
稀疏度G,超前常数L
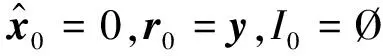
定义:n=[n1,n1,…,nL]T,j=[j1,j2,…,jL]T
g=0,l=0
do
g=g+1

forl=1 toL
rres=LAres(y,C,G,Ig-1,jl),超前残余
求解,参阅文献[10];
nl=‖rres‖2
end for
l=argmax{n}
ig=jl
Ig=Ig-1∪ig
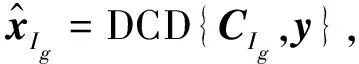
until (‖rg‖2>‖rg-1‖2)或(g>G)
g=g-1;
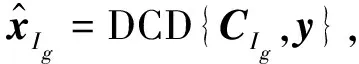
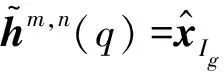
其中rres=LAres(y,C,G,Ig-1,jl)为超前残余(详细计算参阅文献[11]),利用超前残余可以提前确定OMP算法中的当前迭代的有效原子,因此,相比于常规的OMP算法,LAOMP算法具有更好的稀疏重构性能,但是其缺点是增加了算法的复杂度;通过分析LAOMP算法可以知道其计算复杂度主要在于LS问题的求逆过程,本文提出采用DCD迭代算法来求解LAOMP算法中的LS问题,常规的LS问题求解的复杂度为O(P2),在OMP算法迭代中,每次迭代过程中需要求解一次LS问题,因此G次迭代的计算复杂度为O(GP2),对于LAOMP算法来说,假设超前残余步长为L,那么超前残余求解的复杂度为O(LP2),那么LAOMP算法所需的总的复杂度为O(GLP2),根据文献[11]中的描述,超前残余步长L一般不太大就可以获得超过OMP算法的性能。如果采用DCD算法进行LAOMP算法中的LS问题的求解,则所需的计算复杂度为O(GLP),复杂度降低了一个数量级,另外,因为DCD求解算法中仅仅涉及到求和和移位操作,因此可以非常有效地在DSP或FPGA上实现[11-13]。
2 LAOMP稀疏信道估计性能仿真分析
为验证本文提出的方案的性能,本节采用南海某海域的声速剖面对系统进行仿真研究,仿真参数如表1所示;仿真中采用的发射换能器为2个,仿真区域的最深海深为85 m,第1个发射换能器位于水面下40 m,第2个发射换能器位于水面下40.25 m;接收水听器2个,第1个接收水听器位于水面下45 m,第2个位于水面下40.1 m,收发系统的距离为3 km。
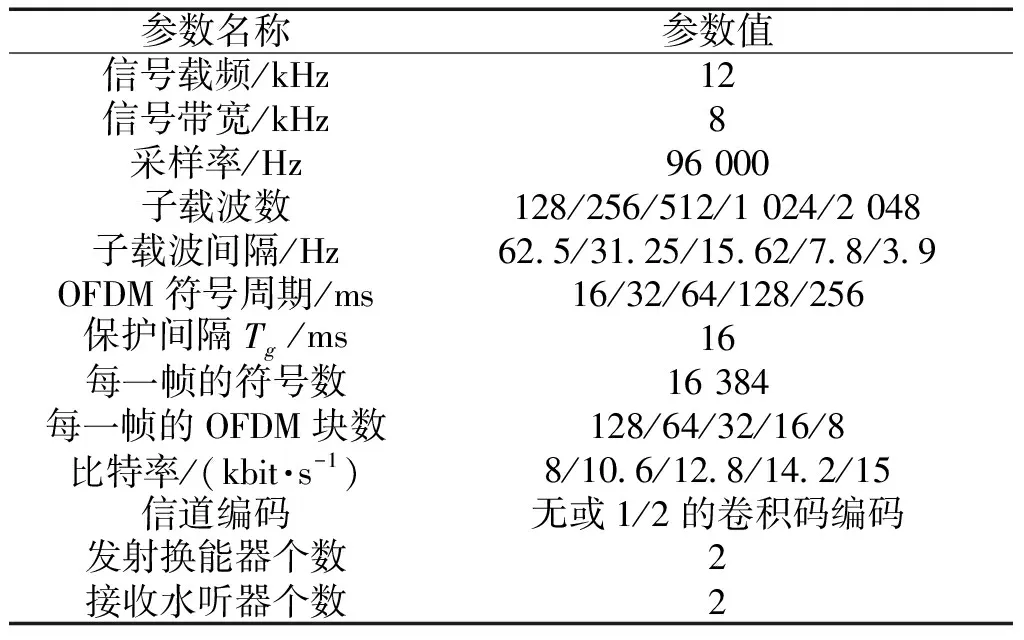
表1 仿真参数Table 1 Simulation parameter
仿真与后续试验中所使用数据帧结构相同。如图3给出了某一个换能器发射的1帧信号的结构,其余配置的帧结构类似。以子载波数为2 048为例,每一帧的总符号数为16 384,因此,能够分成16 384/2 024=8个OFDM符号;相邻OFDM符号之间的保护间隔Tg为16 ms;在每一帧的帧头和帧尾分别插入同步信号,本文采用的是7阶(即127比特)多普勒敏感的伪造声(pseudo-noise,PN)序列,同步信号调制后的长度约为16 ms;为了避免同步信号和相邻OFDM符号之间的干扰,在同步信号和第一个OFDM符号以及最后一个OFDM符号之的保护间隔设定为30 ms。

图3 OFDM数据帧结构Fig.3 Frame structure for OFDM system
本节水声信道仿真采用文献[14]提出的仿真器,该水声信道仿真器在给定信道参数的条件下可以在一定的保真度下模拟水声信道对水声通信信号的影响。本仿真的声速剖面采用的是海试现场通过CTD测量到的声速剖面,海底采用平面海底,海底声速为1 400 m/s,海底介质密度为1 800 kg/m3,仿真中不同的多普勒效应可以通过设定收发平台的运动参数实现。
为了考察OMP算法和LAOMP-DCD算法在静态多途信道下的估计性能,其中仿真和试验数据处理过程中的DCD迭代过程采用的参数如下:接收信号先做幅度归一化,即信号的幅度在区间[-1,1]中,信号幅度定点量化比特数为6或13个比特,最大DCD迭代次数设为32次。仿真水声信道的最大多途扩展为Tg,仿真多途信道的抽头数目为8(相比于信道的多途扩展,该信道满足稀疏信道的特性);多途信道抽头出现的位置服从随机的均匀分布(以符号间隔),信道抽头幅度为0~1的一个随机数,生成的随机信道需做能量归一化处理,仿真中假设稀疏度G已知,同时为避免不必要的计算复杂度,LAOMP-DCD算法中的超前常数L=5。图4出了OMP和LAOMP-DCD算法的归一化均方误差(normalized mean square error,NMSE)。
由图4可以看出,在稀疏信道条件下,由于LS算法信道估计的噪声加强作用,导致信道估计性能受限,OMP和LAOMP-DCD稀疏信道估计算法均优于LS非信道估计估计算法;另外,LAOMP算法优于超前迭代过程的存在,其性能优于OMP算法。幅度量化对LAOMP-DCD算法有一定的影响,但是当量化比特为6时,LAOMP-DCD算法的性能仍然优于OMP算法,但是稍稍弱于13比特量化的LAOMP-DCD算法,13比特量化的LAOMP-DCD算法性能基本上与LAOMP算法相当,从实时实现的角度而言采用6比特量化可以较好地平衡性能与复杂度要求。
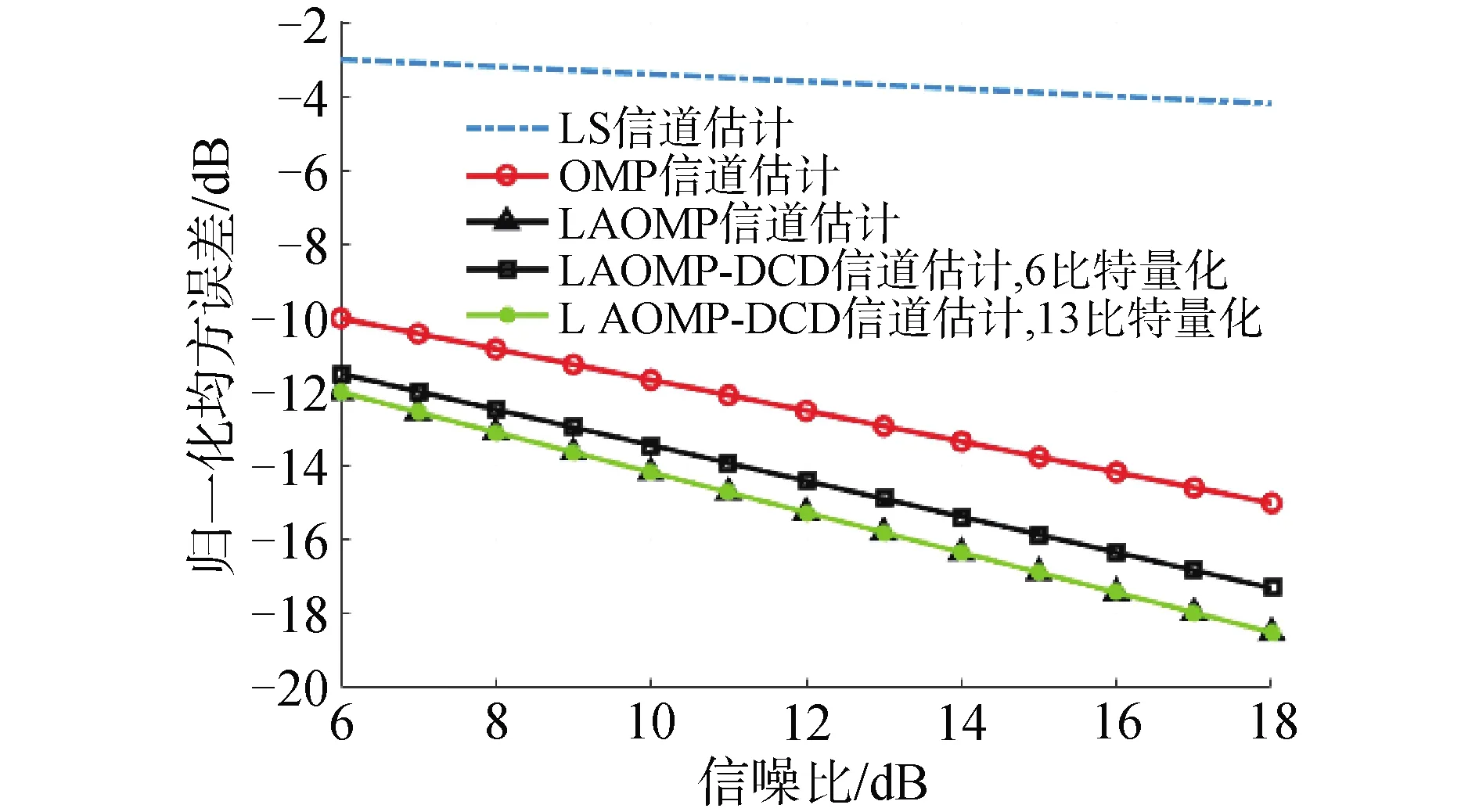
图4 信道估计归一化均方误差性能Fig.4 NMSE performance of channel estimation
图5给出了子载波数为1 024的条件下SIMO、STBC和SFBC系统的BER性能(无信道编码)。由图可知在子载波间隔为7.8 Hz时,SFBC性能优于STBC和SIMO系统,可见,利用子载波间的相干性可以明显改善系统的性能;对于SFBC系统,采用LAOMP-DCD和LAOMP的信道估计的系统性能基本一样;SFBC系统性能优于STBC和SIMO系统的性能,SIMO系统的性能最差;另外,采用LAOMP稀疏信道估计的系统性能优于采用OMP稀疏信道估计的系统的性能,因此后续仿真中不再给出基于OMP稀疏信道估计的SFBC系统的性能分析。

图5 不同系统配置下的BER性能Fig.5 BER performance for different system configurations
图6给出了与图5相同配置条件下的符号估计的均方误差。在SNR为20 dB时,SFBC系统的均方误差小于STBC和SIMO系统的均方误差,分别为2.4 dB和3 dB。均方误差图的结果与图5的BER性能的结果一致。
图7是信道编码系统的BER性能,其余仿真参数与图5的仿真参数一致,由图可知,信道编码可以极大地改善系统的性能;另外,在信道编码条件下,采用LAOMP-DCD和LAOMP进行信道估计的系统性能基本一样。

图6 符号估计均方误差性能Fig.6 MSE performance of symbol estimation for different system configurations

图7 编码系统的性能Fig.7 Performance for coded systems
图8给出了不同子载波数的条件下(即不同的子载波间隔)的系统性能(无信道编码),系统仿真信噪比为15 dB,当子载波数为256时可以获得最优的系统BER性能,随着子载波数的增加系统的BER性能降低(如图,子载波数为512、1024、2 048和4 096时),这主要是由于子载波间隔的减小,系统更容易受载波间的干扰(inter-carrier interference,ICI),最终导致系统性能恶化;另外,子载波间隔太大(如图8,子载波数为128时)也会导致系统的BER性能减低,这主要是由于过大的子载波间隔会导致载波间的相干性降低,同时还会降低系统的频谱效率。

图8 不同子载波条件下的系统BER性能Fig.8 BER performance with different number of carriers
图9给出了存在不同多普勒残余的时候的SIMO、STBC和SFBC系统的BER性能(无信道编码),仿真SNR为15 dB,由图可知,SFBC-LAOMP-DCD系统最优,但是随着残余多普勒因子的增加(大于10-4),3种系统的性能均随之恶化,另外,在较小的多普勒残余时,系统具有较好的时间相干性,因此,STBC系统的性能优于SIMO系统的性能,但是随着多普勒残余量的增加,系统的时间相干性减弱,STBC系统的性能急剧恶化。

图9 不同残余多普勒因子件下的系统BER性能Fig.9 BER performance with different residual Doppler factor
3 SFBC-OFDM系统试验数据处理分析
采用南海某水域的试验数据对本文提出的系统进行了验证。试验采用2条渔船:一条渔船悬挂2个发射换能器,第1个发射换能器位于水面下4 m,第2个发射换能器位于水下4.25 m;另一条渔船悬挂4个接收水听器,第1个接收水听器位于水面下20 m,4个水听器之间的间隔为0.1 m。由于发射换能器和接收水听器非刚性固定,所以实际的深度会有变化。2条船处于随风漂移状态,试验开始时2船距离约为4.1 km。通过GPS可以测得船漂移的速度在0.4~1 m/s的范围。试验数据的发射数据帧结构如图10所示,基本参数如表1所示。试验时首先发射SIMO数据,随后发射STBC的数据,最后发射SFBC数据,发射完毕后再进行下一个周期的发射,本节采用试验中的208帧的数据进行统计分析,在算法比较之前,首先对接收数据进行粗的多普勒估计与补偿,即利用前导线性PN序列和后导PN序列进行平均多普勒的估计(这样做可以避免接收到的PN序列受多普勒影响导致与本地参考PN序列做相关时的失配问题),然后利用粗多普勒估计对接收数据进行粗多普勒的补偿,同时利用同步信号对信道稀疏度进行的预估,以便设定后续OMP算法以及LAOMP-DCD算的稀疏度值G。

图10 发射数据帧结构Fig.10 Data structure for transmitted signals
图11为海试试验的MIMO信道冲击响应,信号采样率为96 kHz,该信道估计是在完成平均多普勒补偿之后通过最小二乘信道估计算法得到的。信号估计过程中把所有的接收数据当作已知训练导频信号就可以对信道的变化状态进行持续估计和跟踪。图11(a)给出了发射换能器1到接收水听器1个信道冲击响应,由图可知在2 000次的信道观测快拍下,信道总体是慢变的,能量较大的抽头为3个,这样的信道多途结构具有稀疏性;图11(b)给出了发射换能器2到接收水听器1个信道冲击响应,同样,由图可知在2 000次的信道观测快拍下,信道总体是慢变的,该信道多途结构同样具有稀疏性。其他信道结构基本类似,此处不再赘述。
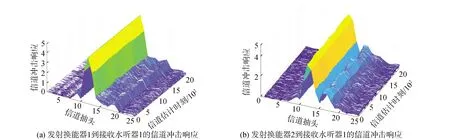
图11 海试MIMO信道冲击响应Fig.11 Channel impulse response of sea trial MIMO channel
图12给出了SIMO、STBC以及SFBC系统的平均BER性能(即所有数据帧误码率的平均)。
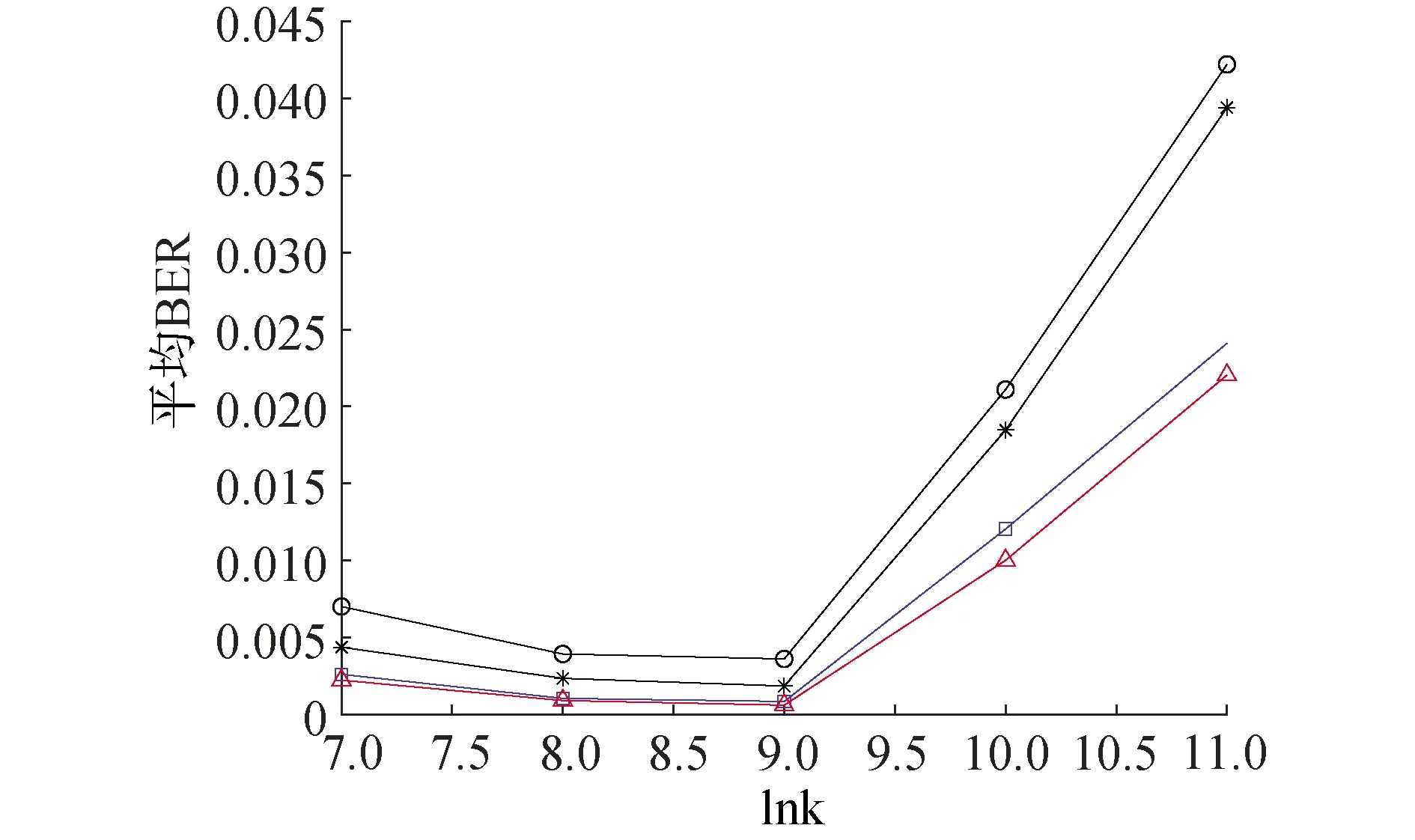
图12 不同未编码系统的平均BER性能Fig.12 Averaged BER performance for different system without coding
在试验条件下:一方面,STBC系统的性能优于SIMO系统,表明STBC系统能够利用时间相干性提高系统的性能;SFBC系统在所有子载波数条件下的性能是最好的,说明可以利用子载波间的频率相干性可以极大的提高系统的性能,但是随着子载波数的增加,子载波间隔减小,由于残余多普勒的存在,因此,载波间的干扰增大,最终导致系统性能恶化,需要采取相应的ICI抵消技术才可以抑制ICI的影响;另一方面,基于提出的LAOMP-DCD稀疏信道估计算法优于OMP稀疏信道估计算法。以上系统采用信道译码之后,子载波数为128、256和512的系统的误码率为0;子载波1 024和2 048的系统的平均误码率不能达到无误码传输。
4 结论
1)提出基于LAOMP的稀疏水声信道估计算法的性能优于传统的OMP稀疏信道估计性能。
2)采用13比特的幅度量化,基于DCD迭代技术的LAOMP(LAOMP-DCD)稀疏信道估计性能与LAOMP稀疏信道估计性能基本一样,但是可以极大地降低在DSP或FPGA硬件实现上的复杂度。
3)采用信道编码技术后,基于LAOMP-DCD稀疏信道估计算法的空频块编码MIMO-OFDM系统的性能在误比特率上具有很大的优势。海试试验结果表明:不同子载波数条件下,基于本文提出的信道估计算法的SFBC MIMO-OFDM系统的平均误码率性能均优于其他方案。

