一种带有动力切换的飞回段迭代制导算法

张博俊， 刘占超， 刘刚

(1.北京航空航天大学 仪器科学与光电工程学院， 北京 100191； 2.北京航空航天大学 前沿科学技术创新研究院，北京 100191)

可重复使用运载火箭(reusable launch vehicle,RLVs)垂直回收任务是目前运载火箭轨道设计领域最复杂、约束最多的一类任务[1]。一个典型的RLVs陆地垂直回收过程的真空飞行段先后经历转弯段、滑行段、减速段3个飞行段[2]，改变RLVs速度方向使RLVs飞向着陆点方向。在火箭上升段飞行期间，由于箭体、飞行环境等因素影响，将积累大量的飞行偏差，若采用分段制导的方式，则转弯段的制导压力过大，不利于制导参数设计。针对这种情况，统筹考虑转弯段、滑行段、减速段RLVs的飞行特点、制导需求，将这3段视为一个整体的逻辑上的飞行段，称之为飞回段，并使用统一的制导算法。通过这种方式，释放单个飞行段制导压力，避免了转弯段、减速段需要装订多段制导参数或者使用不同制导算法的情况。由于垂直回收任务的推进剂限制，在轨道设计阶段，往往使用直接数值优化算法来同时保证制导精度及推进剂最优，如凸优化算法[3-4]、伪谱法算法[5]和预测校正算法[6-8]等。尽管这些算法都是求解多约束最优轨道的有效算法，但这些算法都需要多轮次的离散优化过程，计算量大，难以应用到飞行任务中，仅作为离线轨道设计。迭代制导(iterative guidance method，IGM)是一种广泛应用于国内外各型运载火箭的真空飞行段的制导算法。文献[9-15]分析了迭代制导算法各类改进。在此基础上继续开发适用于RLVs飞回段的制导算法是可行的，且有利于运载火箭的上升段、下降段制导算法的一体化设计。本文首先分析了RLVs飞回段制导算法设计难点和需求，针对转弯段、减速段不同的速度方向需求重新推导了姿态角系数公式；推导了适用于滑行段的变推力迭代制导算法；推导了转弯段目标速度修正公式。其次通过与预测校正制导算法进行对比，验证了飞回段迭代制导算法的有效性。最后开展了初始较大偏差情况下的仿真分析。

1 飞回段迭代制导算法分析

1.1 迭代制导坐标系变更

上升段迭代制导建立在目标点轨道坐标系Os-εζη中，显然不能用该坐标系来描述飞回段RLVs的运动状态。为与上升段火箭的轨迹能够更好地衔接，RLVs垂直回收任务一般采用发射坐标系来描述RLVs运动过程，飞回段迭代制导以发射坐标系作为基准。发射坐标系以运载火箭发射点为坐标原点，x轴指向射向方向，y轴指天，z轴为右手坐标系方向。本文所有公式推导皆基于发射坐标系，因此不再标出脚标。

在发射坐标系下 RLVs的飞回段运动方程为：

(1)

(2)

(3)

式中：x、y、z分别为RLVs在发射坐标系下的3个位置分量；gx、gy、gz分别为引力加速度在发射坐标系下的3个分量；a为RLVs的瞬时加速度；φ、ψ分别为RLVs在发射坐标系下控制变量的俯仰姿态角和偏航姿态角，姿态角公式同传统迭代制导算法：

(4)

(5)

传统迭代制导采用轨道坐标系有效简化了轨道根数与飞回段终点的速度、位置之间的非线性关系，在RLVs垂直回收任务中，对飞回段终点的速度、位置有着明确的约束，可基于约束直接求解姿态角φ、ψ。由此可见，当变更飞回段迭代制导坐标系后，相关思路及公式可以继续使用。

1.2 飞回段制导算法需求分析

RLVs的上升段、飞回段主要在发射系射面内飞行，侧向速度、位置较小，主要速度增量需求集中在发射系x和y轴，图1显示了RLVs飞回段在射面内的速度变化情况。

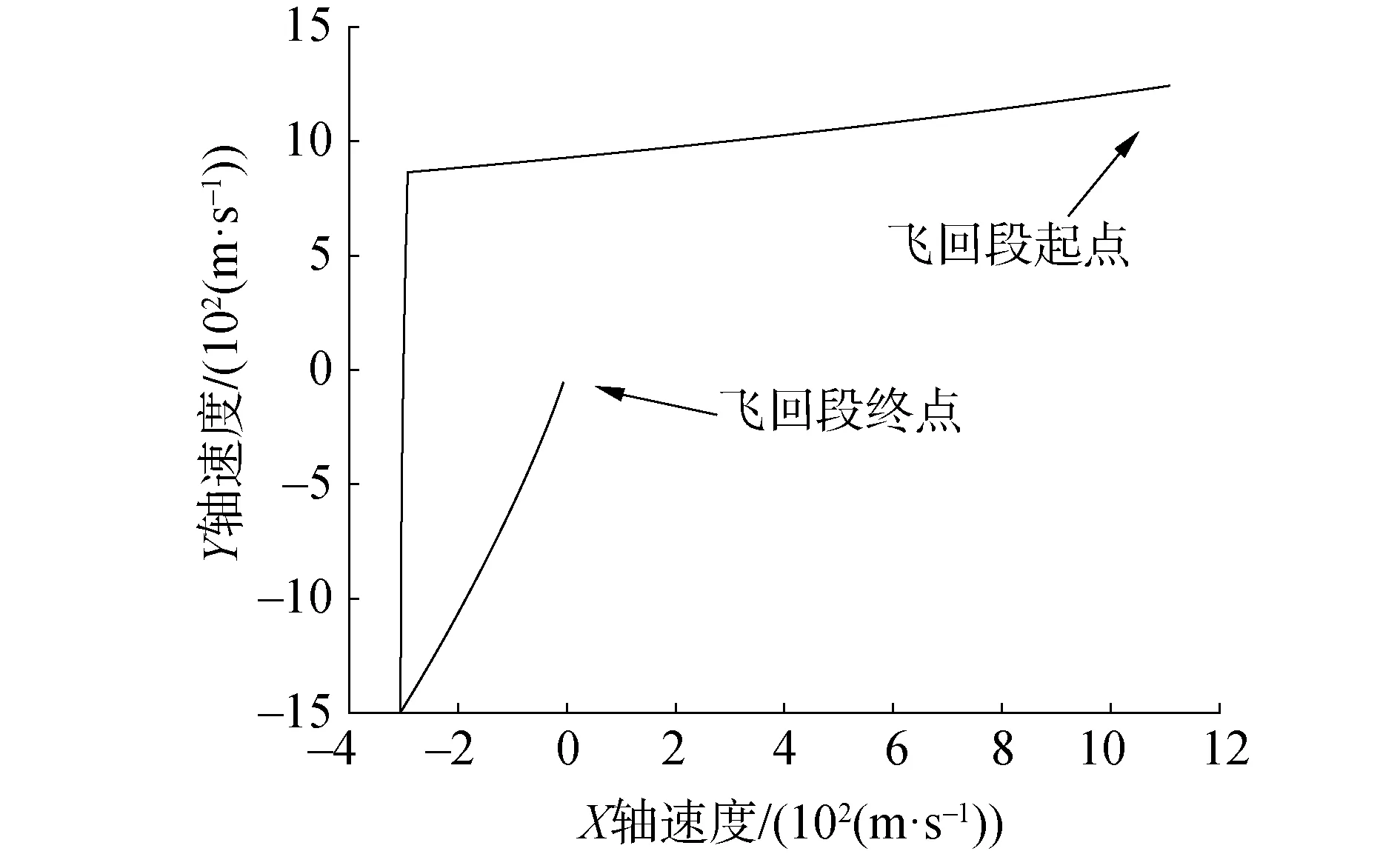
图1 RLVs飞回段速度曲线Fig.1 RLVs flyback phase velocity curves

结合RLVs真空飞行段飞行轨迹及图1中所示的速度曲线，RLVs飞回段有以下几个特点：

1)RLVs飞回段速度曲线如图1所示，转弯段、减速段速度增量需求方向不同，在转弯段不能直接计算到减速段终点的速度需求，需要对传统迭代制导算法进行一定的修改；

2)初始速度、位置与飞回段终点速度、位置相差巨大，连续动力转向方案难以同时满足速度、位置约束，必须采用带滑行段的动力切换方案；

3)RLVs基于运载火箭传统构型设计，火箭发动机仅能进行开关控制，控制变量仅有俯仰、偏航姿态角。单一动力飞行段难以同时满足本段速度、位置约束，因此需要对飞回段整体进行制导方案设计，通过将不同约束分配到各个飞行段的方法满足整体制导精度需求。

2 飞回段迭代制导算法

2.1 发射系迭代制导公式

2.1.1 偏航方向

在算法计算瞬时，运载火箭的总加速度公式为：

(6)

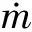
对z轴积分并将小角度假设引入到积分公式中，积分1次：

(7)

积分2次：

(8)

式(6)、(7)中各阶积分公式为：

(9)

(10)

(11)

(12)

定义z轴速度需求为：

(13)

位置需求为：

(14)

将式(13)、(14)代入到式(7)、(8)并整理，可以得到偏航姿态角系数公式：

(15)

2.1.2 俯仰方向

参照式(13)、(14)，定义x轴速度、位置需求公式为：

(16)

(17)

同理，定义y轴速度、位置需求公式为：

(18)

(19)

分别x、y轴进行2次积分，并代入式(16)～(19)可以得到：

(20)

(21)

(22)

(23)

式中：

(24)

其中：

(25)

(26)

(27)

联立式(20)、(21)，得到基于x轴的俯仰姿态角系数方程：

(28)

联立式(22)、(23)，得到基于y轴的俯仰姿态角系数方程：

(29)

2套姿态角系数方程的主要区别是分母项不同，由图2可知，在转弯段速度增量需求主要为x轴负方向，俯仰姿态角接近-180°，由于三角函数的特点，该段只能使用式(29)。同理，在减速段只能使用式(28)。

2.1.3 剩余飞行时间迭代

由于迭代制导剩余飞行时间tf是由视加速度及速度需求共同决定的，与坐标系无关，剩余飞行时间修正公式同原迭代制导：

(30)

式中Δv为根据目标速度及平均重力计算得出的速度需求。

2.2 变推力迭代制导公式

定义转弯段飞行时间为tt，标称轨道滑行段飞行时间为tg，则在tt时间点RLVs从正常推力状态切换到某一指定节流幅度PSW，不同推力节流情况下的τ为：

(31)

对于RLVs陆地垂直回收任务，滑行段为无推力状态，式(31)中PSW在分母项，不能为0，可以设定PSW=0.000 1，即接近于0也不会造成计算错误。

将式(8)按照2段动力模式重新进行推导：

(32)

式中Lu和Ll分别是高低推力工况下的积分公式，同理可得其他各项的2段积分公式：

It=Iu+Il+Lltt

(33)

(34)

St=Sl+Su+Lutg

(35)

Qt=Qu+Ql+Iutg+Sltt

(36)

(37)

用式(32)～(37)代替式(15)～(17)、(26)方程中对应的积分项，则可以得到多段动力情况下的迭代制导姿态角系数方程和剩余飞行时间方程。

2.3 转弯段目标速度修正

由1.2节分析可知，由于RLVs基于运载火箭传统构型设计，单一动力飞行段难以同时满足速度、位置6个约束。由RLVs飞回段动力切换方案可知，转弯段的主要目标是调整水平速度方向，使RLVs滑行段轨迹近似抛物线，“投”向减速段起点。在飞回段初始较大位置偏差的情况下，若依然要求转弯段速度约束为标称轨道设计值，将会造成RLVs滑行段飞行轨迹的大幅平移，难以达到减速段起点。

针对该情况，需要对转弯段迭代制导目标速度进行在线修正，通过分别预估RLVs在各坐标轴的位移需求的方式，反算目标速度修正量。

定义xt、yt、zt分别为减速段起点位置约束，忽略姿态角小量，并对式(1)进行2次积分，得到：

(38)

若保证RLVs经过滑行段后能准确到达减速段起点位置，则转弯段终点的x轴速度修正量为：

(39)

同理，可得y、z轴速度修正量公式：

(40)

(41)

(42)

(43)

通过式(39)、(41)、(43)的速度修正，解放了转弯段的制导能力，将初始位置偏差转换为速度增量需求，保证RLVs经过滑行段飞行后，能够抵达指定位置，并由减速段修正全部速度增量需求。

2.4 飞回段制导算法流程

由图1可知，转弯段、减速段速度增量需求方向不同，由2.1.2节分析可知，在转弯段和减速段使用的俯仰姿态角系数计算公式不同。

因此，在整个飞回段迭代制导算法中，将采取双迭代目标以及俯仰姿态角系数计算公式切换的方法实现RLVs不同飞行阶段的制导需求：在转弯段，设置推力低工况时间同滑行段飞行时间tg，制导目标是减速段的起点，使用式(29)计算俯仰姿态角系数；在减速段，设置推力低工况时间为0，设置制导目标为减速段终点，使用式(28)计算俯仰姿态角系数。算法流程图如图2所示。

通过以上分析可以看出，飞回段迭代制导算法仅需更改制导目标及低工况工作时间即可实现不同飞行阶段的制导需求，算法结构清晰、简单，便于箭上计算机实现。

3 仿真校验

以某型号RLVs陆地垂直回收任务为例，对本文提出的飞回段迭代制导算法进行验证。并与预测校正制导算法的进行对比。需要注意的是，预测校正制导算法是对RLVs垂直回收任务飞行轨道的全程进行优化，在本次对比中截取了飞回段对应的姿态角及飞行轨迹。

3.1 姿态角输出对比

为合理对比2类制导算法的输出情况，分析本算法的有效性，在输入偏差范围内，随机生成1 000组偏差，并分别开展仿真，在同偏差输入情况下开展比较分析。预测校正制导算法为从RLVs分离后到着陆的整体轨道优化，从中截取飞回段制导结果。由于RLVs主要在射面内飞行且偏航姿态角较小，因此主要分析俯仰姿态角输出的正确性。

图3中画出了2类制导算法的转弯段俯仰姿态角曲线。预测校正制导算法通过工作时间满足x轴速度需求，输出俯仰姿态角保持-180°；飞回段迭代制导算法修正初始偏差，并计算滑行段位移对转弯段目标速度修正，输出俯仰姿态角略有角度。

图4中画出了两类制导算法的减速段俯仰姿态角曲线。预测校正制导算法采用零攻角减速策略，因此输出姿态角略呈弧形；飞回段迭代制导算法采用线性程序角策略，输出姿态角呈线性，但两者间差距较小。

3.2 单条偏差轨道仿真结果对比

2类制导算法在同一初始偏差下的仿真结果与标称轨道的对比见表1。

图2 RLVs飞回段制导算法流程Fig.2 RLVs flyback phase guidance algorithm process

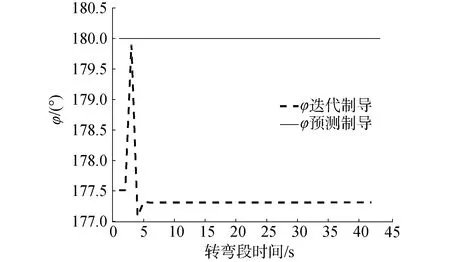
图3 RLVs转弯段俯仰姿态角曲线Fig.3 RLVs turning phase pitch angle curves

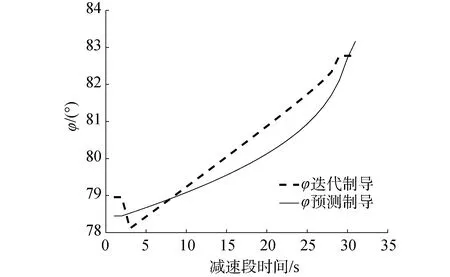
图4 RLVs减速段俯仰姿态角曲线Fig.4 RLVs deceleration phase pitch angle curves

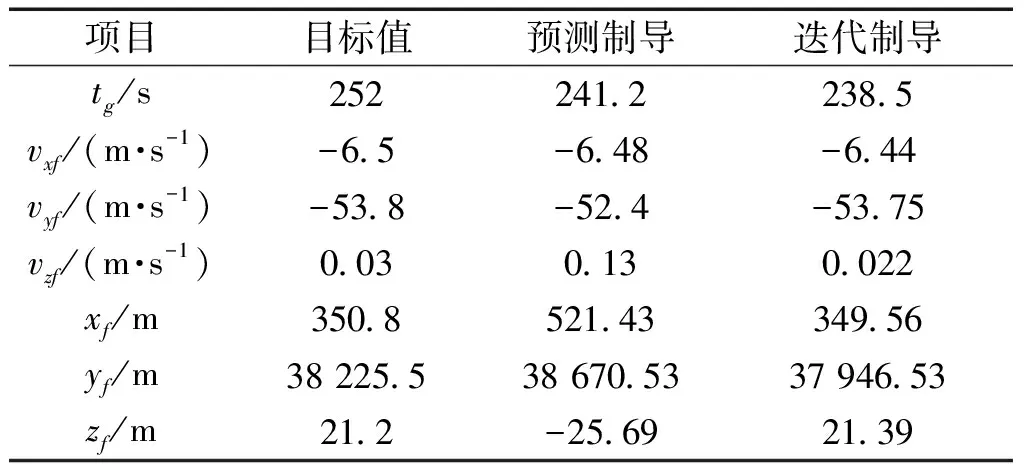
表1 仿真结果分析Table 1 Analysis of simulation result

可见，飞回段迭代制导算法可将转弯段、滑行段、减速段作为一个逻辑飞行段统筹考虑，具有较高的制导精度。

3.3 仿真结果分析

为更好地校验制导算法的鲁棒性和准确性，进行了1 000次蒙特卡洛打靶仿真计算。输入偏差情况见表2。其中速度、位置偏差按照随机矢量方向加入到初始偏差。

图5、6中显示了RLVs在飞回段制导算法导引下从较大的起始速度、位置偏差飞行至指定目标点的飞行轨道，算法收敛效果较好。

经过统计分析，减速段终点的RLVs速度、位置与目标值的偏差的均值、方差情况见表3。

表2 输入偏差值Table 2 Input deviation values

图5 RLVs飞回段制导轨道位置曲线Fig.5 RLVs flyback phase guidance trajectory position curve

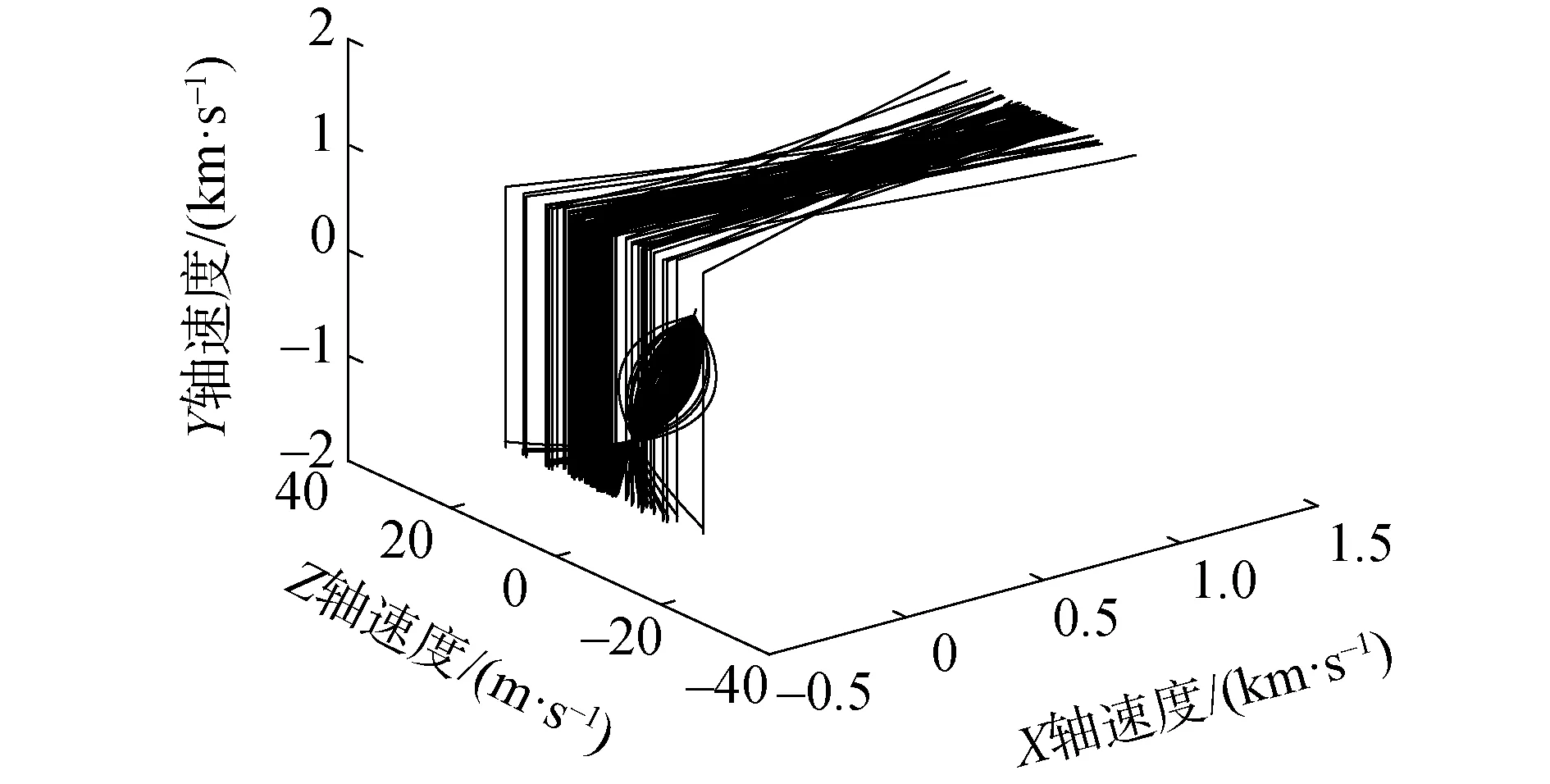
图6 RLVs飞回段制导轨道速度曲线Fig.6 RLVs flyback phase guidance trajectory velocity curve

表3 仿真结果Table 3 Simulation results

为验证飞回段迭代制导的计算效率，同步使用预测校正制导算法对同样的1 000组偏差开展了仿真分析，计算时间对比见表4。

表4 仿真时间Table 4 The simulation time

可见，经过飞回段迭代制导算法的修正，在较大的飞回段初始偏差的情况下，制导算法实现了精确的跨飞行段段制导，仿真结果表明算法除y轴位置偏差较大外，具有较高的制导精度。

y轴位置偏差产生的原因是，在转弯段制导算法计算减速段起点的y轴速度修正量时，使用了平均重力加速度，也就是式(39)、(40)。从图6可以看出，由于RLVs滑行段飞行时间长、高度变化大，重力存在一定的变化，使用平均重力假设将造成一定的方法误差，进而造成y轴位置偏差较大。在减速段时，由于RLVs控制方法限制，无法修正y轴位置偏差。

由于y轴位置偏差主要体现在高度偏差上,对于RLVs垂直回收任务，约束较为宽松。因此带有动力切换的飞回段迭代制导算法满足RLVs垂直回收任务的制导要求。

4 结论

1)通过论证、分析，转弯段、滑行段、减速段作为一个整体逻辑飞行段并配备统一构架的制导算法的思路是可行的，对初始偏差较大的RLVs垂直回收任务具有较好适应性。

2)通过仿真分析验证了飞回段迭代制导算法在较大初始偏差情况下的制导效果，统计结果表明飞回段迭代制导算法计算时间少、精度高、鲁棒性强。

本文提出的飞回段迭代制导算法基于平均重力假设开展算法设计，除高度偏差较大外，能够严格约束垂直方向速度偏差，以及水平方向速度、位置偏差，整体符合垂直回收再入要求，具有较好的工程实用价值。后续将进一步在非平均重力情况下开展算法研究，实现对再入点约束的全面满足。