垂直发育裂隙介质中PP波扰动法近似反射系数研究

何现启， 彭凌星， 朱自强， 鲁光银

(1.湖南省交通规划勘察设计院有限公司, 长沙 410200； 2.中南大学地球科学与信息物理工程学院， 长沙 410083)

通过对反射系数的近似研究，可以弄清裂隙介质中反射系数的非线性问题转为线性问题，进而利用这些特性进行参数反演，有利于提高反演速度。对相关工作，中外学者已开展了部分研究。Quintal等[1]通过一维模型数值分析，研究了非饱和岩层中饱和度变化及地震波频率对地震波反射系数的影响。冯润海[2]运用MATLAB软件对各向异性典型模型反射系数和振幅数据进行了比较,讨论了各向异性介质中地震波反射系数的变化特征。王小杰等[3]利用弱黏弹性近似推导了黏弹性介质反射系数近似公式,精确地反映了地震波的传播规律。付欣[4]指出AVO(amplitude variation with offset)分析的一般线性反射系数近似公式与精确公式之间还存在较大误差。Zhao等[5]研究表明，在扩散黏滞性介质中的反射系数的大小不仅与入射角和介质参数有关，而且还与地震波频率相关。许茜茹等[6]研究表明，具有比横向各向同性(TI)介质的正交各向异性介质通常需要9个独立参数对其进行描述,这使得对传播特征的计算更为复杂且在奇异点(慢度面的鞍点和交叉点)附近的反射与透射(R/T)系数的求解不稳定。陈长敬等[7]采用基于匹配追踪(matching pursuit, MP)的多子波分解技术可以得到准确的反射系数。单俊臻等[8]推导出一种新的PP波HTI介质反射系数一阶扰动近似公式，提高了炮检距信息的利用率。张繁昌等[9]研究结果表明，采用傅里叶级数反射系数公式能够准确用于进行裂缝密度预测。陈德元[10]基于地震薄层反射系数谱提出了线性谱反演约束方法。Song[11]研究了具有水平对称平面的单斜介质中的近似反射系数，并通过数值计算证明二阶近似公式具有较高的精度。

1 裂隙介质的精确反射透射系数

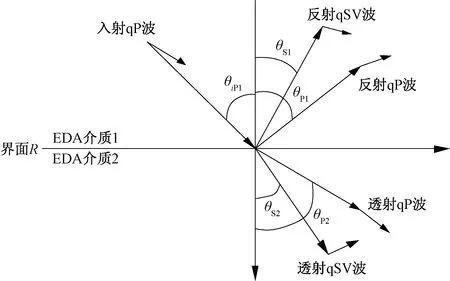
图1中, 分别用下标1和2表示两种介质的弹性参数，当qP波UiP入射至介质界面时，产生反射qP波U2和反射qSV波U3，透射qP波U4和透射qSV波U5[12-16],U表示各种波的质点偏振位移。

在xoz平面内PP波可表示如下。

入射qP波：

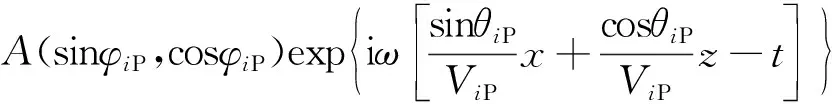
(1)

反射qP波：

θiP1为入射波的入射角；θS1为反射qSV波的反射角; θP1为反射qP波的反射角;θS2为透射qSV波的透射角; θP2为透射qP波的透射角图1 界面处入射qP波、反射波和透射波示意图Fig.1 Schematic diagram of incident qP wave, reflected wave and transmitted wave at the interface

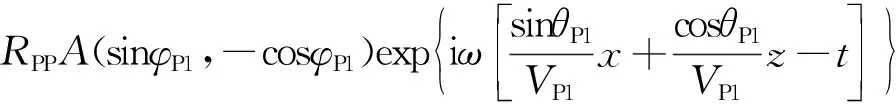
(2)

式中：UiP、U2分别为入射波和反射波的质点偏振位移；A为qP波的振幅；ω为圆频率；x、z为几何坐标；t为时间；RPP为以位移表示的qP反射波的反射系数；φ为与各种波相关的偏振角[17-20]，下标iP和P1分别为入射波和反射波。

在边界处位移连续，即

(3)

应力连续，即

(4)

式中：

当z=0时，有

(5)

式(5)中：UiPx、U2x、U3x、U4x、U5x分别为入射波、反射波qP和反射qSV波，透射qP波和透射qSV波的x分量。

将式(1)、式(2)代入式(5)得

(6)

式(6)中:RPP、RPS、TPP、TPS分别为以位移表示的qP反射波、qSV反射波、qP透射波和qSV透射波的反射系数和透射系数。

根据裂隙介质的弹性矩阵，将波函数代入边界条件，整理可得EDA介质qP波入射的矩阵形式拟Zoeppritz方程为[21-23]

MR=N

(7)

式(7)中：R=(RPP,RPS,TPP,TPS)；M、N分别为EDA介质参数和与入射角有关的系数矩阵，具体表示如下。

(8)

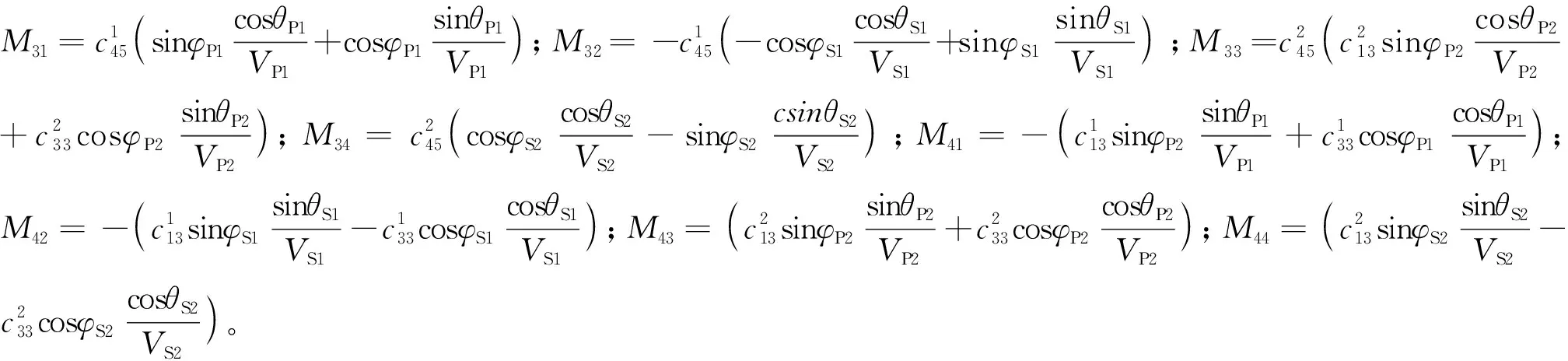
N=[N1,N2,N3,N4]T

(9)

式(9)中：

其中c为弹性系数矩阵的元素。

利用Cramer准则，可确定地震波的反射、透射系数解析表达式为

R=M-1N

(10)

式(10)即为裂隙介质中qP波入射的反射、透射系数精确表达式。

2 弱各向异性介质中P波反射、透射 系数

2.1 弱各向异性介质中入射和透射波P的慢度向量和偏振向量

为便于计算，假设地震波入射平面与xoz平面重合，如图2所示。在一般各向异性介质中，在界面处各产生3种反射波和透射波，其中P表示纵波，S1表示SV波，S2表示SH波。图2中，n为分界面的法向向量，p0(0)为各向同性介质中P波的慢度，p0(1)=p0(2)和p0(4)=p0(5)分别为反射和透射横波的慢度，i、j分别为入射P波与反射波的相角，g0(0)为入射P波的偏振向量，在弱各向异性条件下，慢度向量可以表示为摄动形式[24-27]。

图2 背景介质中零方位角(入射平面为xoz)的 R/T波示意图Fig.2 The schematic diagram of R/T in xoz plane for background media

p(N)≈p0(N)+δp(N)

(11)

式(11)中：p(N)为各向异性介质中地震波的慢度向量；δp(N)为加入的摄动量，N=0、1、2、3分别表示入射P波、反射S1、反射S2、反射P波，N=4、5、6分别对应于透射波S1、S2、P波；p0(N)为各向同性介质中的慢度向量，具体表示为

(12)

式(12)中：a、β分别为各向同性介质中P波和S波的速度。

(13)

式(13)中:δc(0)为入射波的相速度与各向同性介质中相速度的偏差，其表达式为

(14)

由式(11)、式(12)可得在界面Σ上，慢度的切向分量bi可表示为

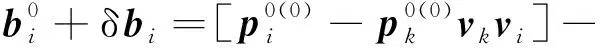
(15)

式(15)中：vi为速度分量。

(16)

在弱各向异性条件下，式(11)可表示为

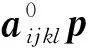
(17)

式(17)中：ξ(6)为法向向量；δbi、δξ(6)vi分别为弱各向异性介质中透射波慢度的切向和法向分量的扰动量。

由式(15)～式(17)可得

(18)

由式(15)、式(18)可得弱各向异性条件下，透射波的慢度为

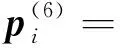
(19)

偏振向量可表示为

g(N)≈g0(N)+δg(N)

(20)

(21)

式(21)中：Φ为介质1中的偏振角；Ψ为介质2中的偏振角；g0(0)、g0(1)、g0(2)、g0(3)、g0(4)、g0(5)、g0(6)分别代表入射P波，反射S1、S2、P波，透射波S1、S2、P。

(22)

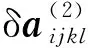
在上述结果基础上，可以对边界条件进行线性化,进而推导出各种波的反射、透射系数表达式。

2.2 弱各向异性介质中PP波反射系数

依据Vaclav Vavrycukand Ivan Psenck(1998)的结论，结合将式(12)、式(19)代入(x，z)平面内的可得PP波反射系数表达式为

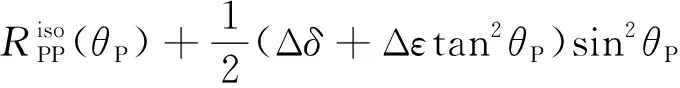
(23)

(24)

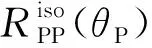
假设入射平面与(x,z)面之间的夹角为φ，弹性参数可表示为

(25)

式(25)中:c11、c′11分别为旋转角度φ后的介质弹性系数及未经转换的弹性系数。

由Thomsen(1993)[x-z]平面内的PP波反射系数表示为

(26)

式(26)中：Δc33为弹性系数；Δρ为介质密度；Δε*为各项异性系数的扰动量。

弱各向异性介质中PP波的反射系数RPP(φ,θP)的计算公式为

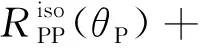
(27)

式(27)中：Δ为拉普拉斯算子。

3 HTI介质中的PP反射系数

依据HTI介质弹性参数，式(27)可简化为

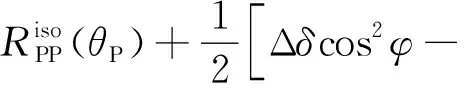
Δδcos2φsin2φ)sin2θPtan2θP

(28)

当φ=π/2，且假设入射面与介质的垂直各向同性面重合，则式(28)可简化为

(29)

4 裂隙介质中PP反射系数

当HTI(horizontal transverse isotropy)介质的对称轴与x轴之间有一定夹角φ0时，可以看成是裂隙EDA(extensive dilatancy anisotropy)介质，其弹性系数矩阵为

(30)

其PP反射系数为

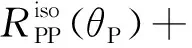
(31)

将各向异性系数代入式(31)可得

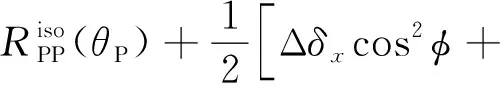
Δεzcos2φsin2φ+2Δε16cos2φsinφ+

2Δε26sin3φcosφ]sin2θPtan2θP

(32)

式(32)中:Δεx为各向异性系数的微小摄动量；RPP(φ,θP)为方位角φ、倾角θP方向的PP波反射系数。

5 算法验证

为了验证所推导的PP波反射系数的近似公式[式(28)和式(31)]的准确性和计算精度，通过建立HTI及裂隙介质的数学模型，通过数值计算验证近似公式与精确公式计算误差，以便确定其应用范围，对实际勘探的应用给与指导。

5.1 HTI介质中PP波反射系数

模型1 HTI参数如表1所示。表1中，VP0、VS0分别为介质对称轴方向的纵波和横波速度，ε、δ、γ为Thmosne各向异性系数，ρ为介质密度。将相关弹性系数代入式(10)及式(28)便可得到HTI介质中地震波的精确反射系数及其近似值，采用MATLAB求解，结果如图3所示，近似值与精确值得绝对误差和相对误差计算结果如图4所示，反射系数随入射角的变化关系如图5所示。

表1 模型1弹性参数Table 1 Elastic parameters of model 1

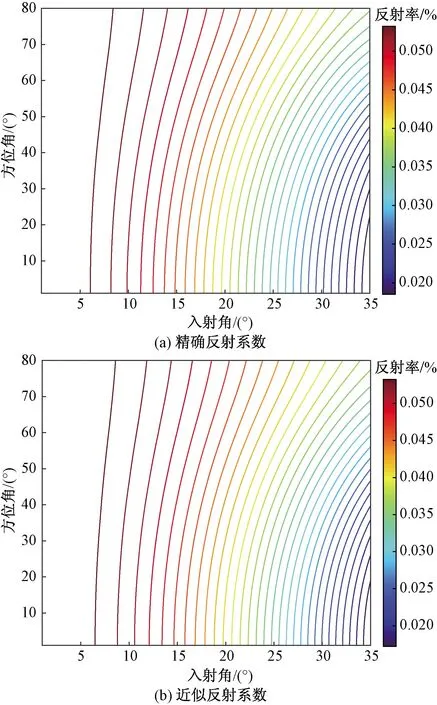
图3 HTI介质PP波反射系数Fig.3 Reflction coefficient of PP wave in HTI media

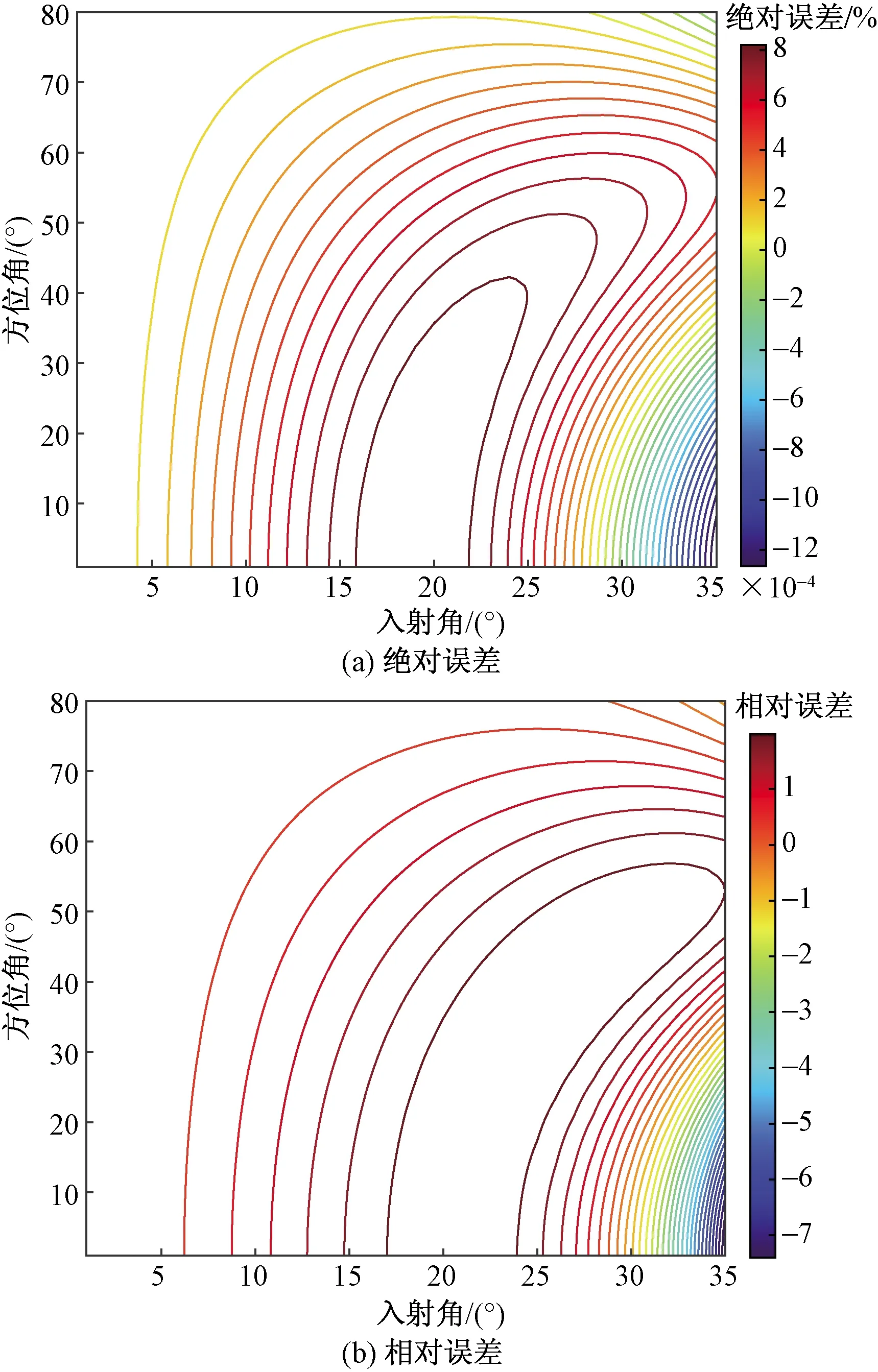
图4 HTI介质中PP波近似反射系数误差Fig.4 Approximation reflection coefficient error of PP wave in HTI media

图5 HTI介质 PP波反射系数与入射角的关系Fig.5 Relationship between PP wave reflection coefficient and incidence angle in HTI media

由图3～图5可知，在HTI介质中，在弱各向异性条件下，式(28)计算精度较高，相对误差在4%，绝对误差在6×10-4以内。反射系数随入射角增大先变小，后增大，在50°左右达到极小值，这可为测线的激发点及采集器的布置提供依据，便于提高数据的信噪比，提高数据采集质量。

5.2 裂隙介质中PP波反射系数

将模型1的弹性矩阵绕z轴旋转60°，则两层裂隙介质的弹性矩阵为

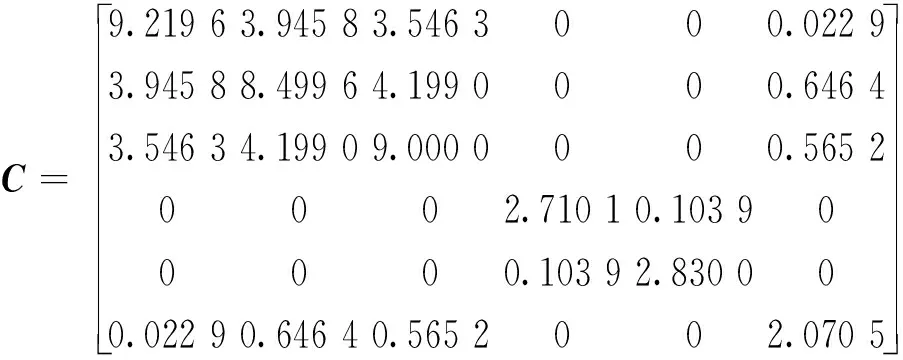
(33)

(34)

通过求解式(10)和式(31)即可得到裂隙介质中PP波的精确反射系数和近似反射系数，结果如图6～图8所示。

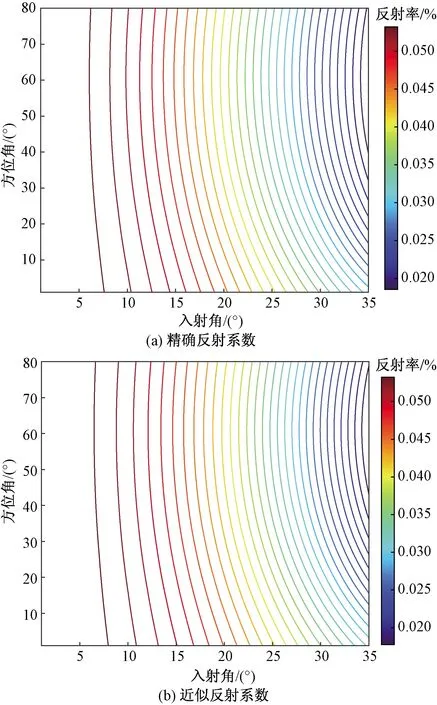
图6 EDA介质中PP波反射系数Fig.6 Reflection coefficient of PP wave for EDA media

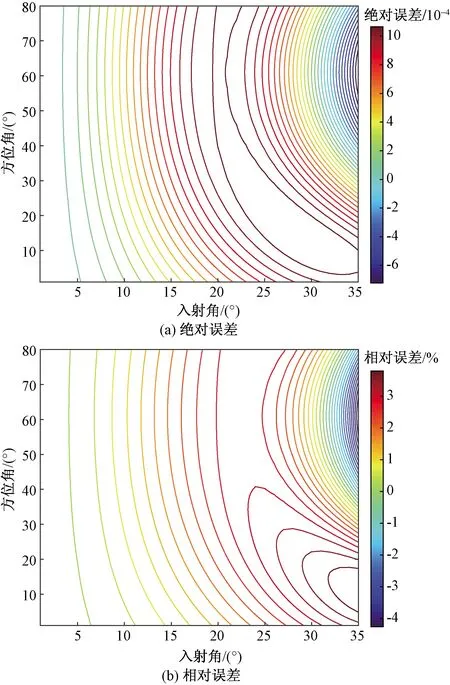
图7 EDA介质中PP波近似反射系数误差Fig.7 Approximation reflection coefficient error of PP wave for EDA media

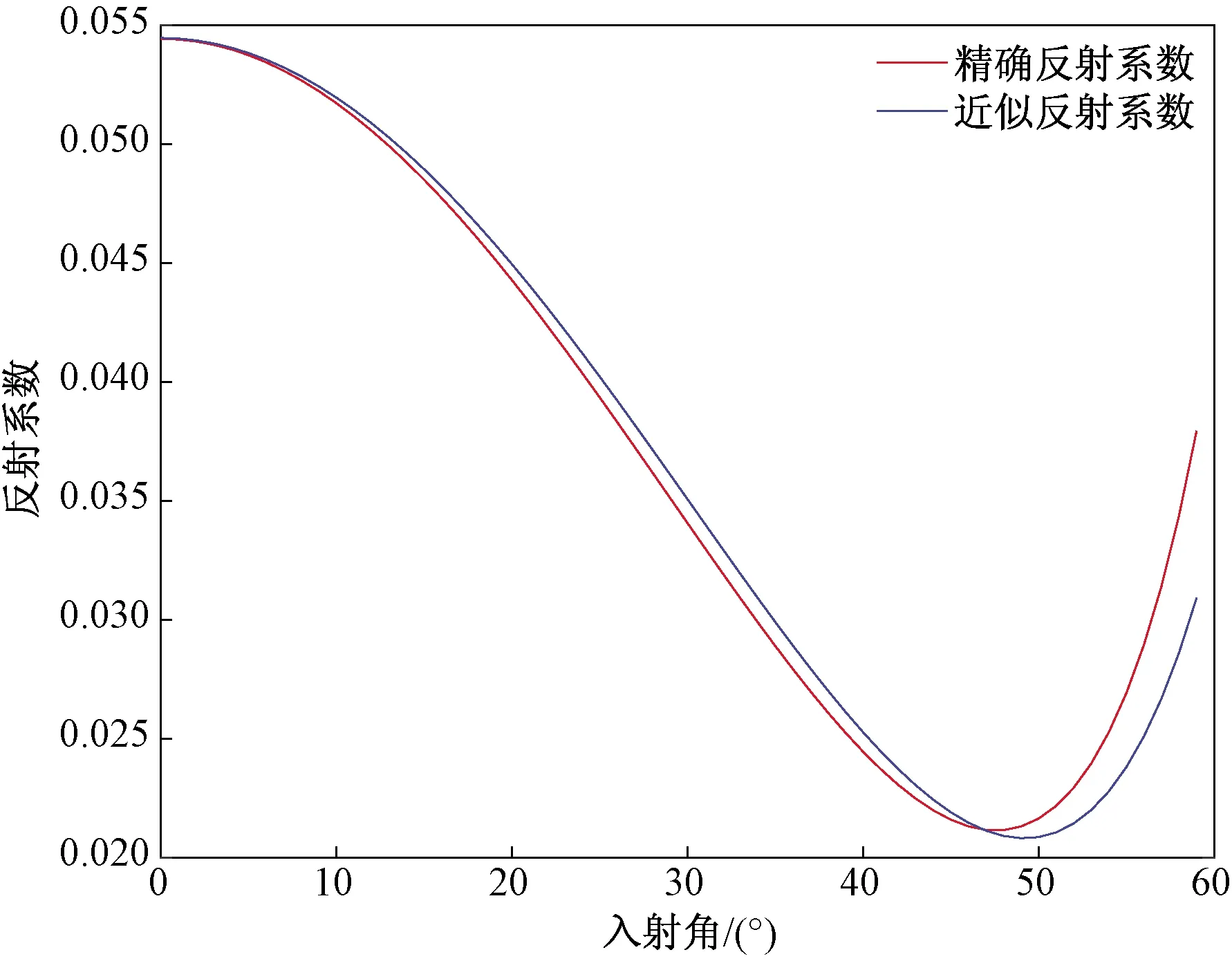
图8 EDA介质PP波反射系数与入射角的关系Fig.8 The relationship between reflection coefficient of PP wave and incident angle for EDA media

分析图6～图8可知当入射角在0°～40°时，模型1裂隙介质的近似反射系数绝对误差在2×10-3以内,相对误差在4%以内。由图8可知，随着入射角的加大其计算误差有所增加。

虽然近似计算公式[式(31)]是在弱各向异性条件下求解得到的，但是对于各向异性较强的介质也成立，通过模型3的计算做进一步分析。模型参数如表2所示，参数含义同模型1。

旋转所得裂隙介质的弹性系数为

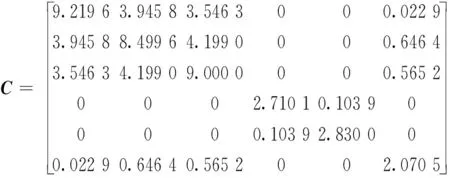
(35)

(36)

通过求解式(10)和式(31)即可得到裂隙介质中PP波的精确反射系数和近似反射系数，结果如图9～图11所示。

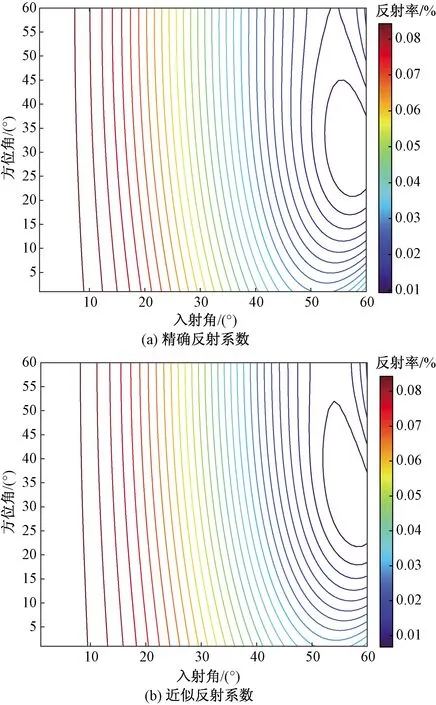
图9 模型2 EDA介质PP波反射系数Fig.9 Reflection coefficient of PP wave of EDA media for model 2

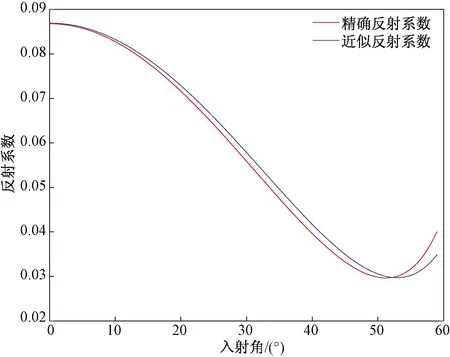
图11 模型2 EDA介质 PP波反射系数与入射角的关系Fig.11 The relationship between reflection coefficient of PP wave and incident angle for EDA media modle 2

由图9～图11可知，当各向异性系数达0.2时，其绝对误差为4×10-3，当入射角增大到60°时其相对误差接近25%，但入射角在0°～45°范围时，其相对误差仍然小于10%。由此可见当各向异性较强时，在入射角相对较小的情况下，式(31)仍然有效。

6 结论

通过研究HTI及裂隙介质中地震波的反射特征，得出如下结论。

(1)通过求解各向异性介质中地震波的Christoffel方程，推导了HTI介质及裂隙介质中PP波、PS1波、PS2波的反射系数精确表达式。

(2)通过对各向同性介质进行微小扰动，模拟弱各向异性条件，采用扰动法求解得到裂隙介质中地震波反射系数的近似表达式。

(3)计算结果表明，对HTI介质近似公式计算精度较高，相对误差在4%以内，入射角对其影响较小。

(4)对裂隙介质，当各向异性系数较小时(小于0.1)，近似解的相对误差在4%以内，入射角的加大其计算误差有所增加，但不超过7%。

(5)当各向异性系数增大时，误差相应增加，但当地震波的入射角为0°～50°时，其近似解精度较高，甚至在各向异性系数都取0.2时其相对误差仍然保持在7%以内。