光由光密介质射向光疏介质时半波损失的条件
邱慧斌,吴俊杰,肖东华,胡天一,钟乘杰,李晓彬
(南昌大学 物理系,江西 南昌 330031)
波从波疏介质射向波密介质时(图1中介质1的折射率小于介质2的折射率时),在反射过程中,反射波在离开反射点时的振动方向相对于入射波到达入射点时的振动相反,或者说,反射波相对于入射波相位突变π,这种现象叫做半波损失[1,2]. 但这个定义中的“振动相反”,在某些情况下是不好界定的,比如入射角为π/4时,根据反射定律,反射角也为π/4,那么此时反射波和入射波垂直,于是反射波在离开反射点时的振动方向相对于入射波到达入射点时的振动相同还是相反是无法定义的.
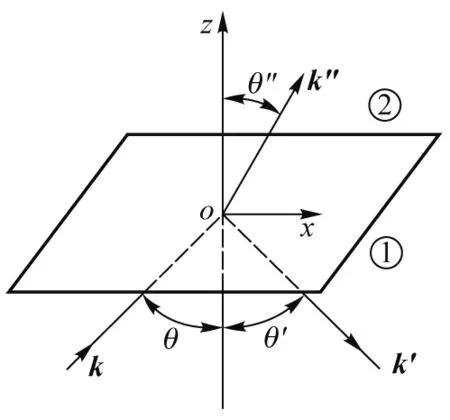
图1 光的反射和折射示意图
为了使得以上的定义仍然发挥作用,需要对正方向进行规定,即规定图2中光的电场分量箭头所指方向为正方向. 如此,则以上的半波损失的定义仍然适用. 但还是存在不足,比如,在图2(b) 中,当介质1的折射率小于介质2的折射率且入射角为0时,根据反射定律,反射角也为0,此时发现:反射波在离开反射点时的振动方向相对于入射波到达入射点时的振动相反,但按上述正方向的规定,反射波相对于入射波相位并未突变π. 这个不足可以通过修改正方向的规定而克服,比如可修改图2(b) 中反射波电场分量箭头方向为负向. 但是作这个修改会产生另一个问题,即考虑在图2(b) 中,当入射角为π/2时,根据反射定律,反射角也为π/2,此时发现:反射波在离开反射点时的振动方向相对于入射波到达入射点时的振动相反,但是此时按修改后的正方向的规定,反射波相对于入射波相位却未改变.
这样修改正方向的规定虽然消除了一个不足但又产生了另一个不足,此外还有如下缺点:1)对于一般情况,修改后的正方向不直观;2)要修改教科书中常用的菲涅耳公式,这会给菲涅耳公式的使用造成一定困扰;3)根据菲涅耳公式得出的已有结论需要重新审查,常用结论使用前需要再次确认是否正确,多出了检查过程. 反之,则没有以上3点缺陷. 综合以上考虑本文仍采用图2中正方向的规定.

图2 光的电场和磁场垂直和平行分量正方向的规定示意图
半波损失是大学物理中一个重要的概念和知识点,它通常作为用于验证光的电磁理论[3]正确性的一个例子,同时在涉及波的相干叠加问题[4]时需要对它特别加以考虑. 然而就一束光而言,往往很难笼统地说是否有半波损失[4],因此现有文献中的讨论往往有限制且不完整. 比如,郭硕鸿著的《电动力学》[3]中提到“在E⊥入射面情形,由(2.12)式,因为当ε2>ε1时θ>θ″,因此E′/E为负数,即反射波电场与入射波电场反相,这现象称为反射过程中的半波损失.”读到这句具有分类性质的语句时,我们自然地想要穷举下去,而这里只提到“E⊥入射面情形”情形,那么E∥入射面的情形呢?还有一般情形呢?于是很自然地,我们自己去把这两种情形补齐,但是发现:在E∥入射面情形,仍考虑“ε2>ε1,θ>θ”的情况,E′/E为负数是有条件的,这个条件是θ+θ″>π/2. 接下来,我们自然想问:如果半波损失是在一定条件下才能发生,那么这个条件是什么?对于既非平行又非垂直的一般情形,这个条件又是什么?既然ε2>ε1时发生半波损失是有条件的,它不一定会发生半波损失,那么ε2<ε1时,有没有可能发生半波损失?
我们查阅了相关教材与文献[4-8],发现都没有完整给出反射波与入射波间的相位差. 因此,无遗漏地清楚阐明反射光什么时候将发生半波损失是非常有必要的,这成为本文的重要目标. 本文将从菲涅耳公式出发,通过对反射波和入射波振幅的比值关系进行详细解析推演、作图呈现和分析讨论,给出反射光和入射光相位差在折射率-入射角空间的详细分布图,研究表明当光束由光密介质射向光疏介质时反射波也可能发生半波损失;而当光束由光疏介质射向光密介质时反射波也不是一定会发生半波损失.
1 结果
为了理解反射波与入射波之间相位差对入射角和相对折射率的依赖关系,从麦克斯韦方程组出发,得到边值关系,然后利用边值关系求得与著名的菲涅耳公式[3,4,9-11]一致的入射波、反射波和折射波的振幅关系如下:
(1)
为方便讨论,引入E⊥入射面时的反射波与入射波之间的相位差[4]:
(2)
及E‖入射面时的反射波与入射波之间的相位差:
(3)
以上公式以图3—图9和表1、表2清晰阐述如下. 从图3和图5可以看出,当光从光密介质射向光疏介质时,反射光也可能发生半波损失(见图3中线段c及图5中线段c和e,亦见表1和表 2);从图5可以看出,光的电场分量平行于入射面时且入射角在大于等于0和小于布儒斯特角时(图5中线段a和区域I),反射光和入射光的相位差则为-π[指反射光平行电场分量的方向与图2(b) 中E′所指方向相反];从图5亦可以看出,当光束由光疏介质射向光密介质时反射波也不是一定会发生半波损失,比如:光的电场分量平行于入射面时且入射角在大于等于0和小于布儒斯特角时(图5中线段b和区域IV),反射光和入射光的相位差则为0[指反射光平行电场分量的方向与图2(b) 中E′所指方向相同〗. 另外,本文给出了反射波和入射波之间相位差的所有细节,这为涉及反射波和入射波相位差的问题——比如波的相干叠加问题[4]——的解决提供了便利.
图3中横坐标为入射角θ,是入射光线与入射表面法线的夹角(见图1),其取值范围为[0,π/2],其中θ=0表示光垂直射向入射表面;θ=π/2表示光平行于入射表面;θ=θB=arctann21时,即入射角为布儒斯特角时,折射角和反射角之和为π/2,此时反射光变为垂直于入射面偏振的完全偏振光[3](见图4);θ=θc=arcsinn21时,即入射角为全反射临界角时,将发生全反射[4]. 纵坐标为介质2相对于介质1的折射率n21,含义为n21=n2/n1,其取值范围是(-∞,+∞),本文聚焦于n21∈(0,+∞)的情况,折射率为零和负折射率情形将另文研究.n21=0+表示光由光密介质射向光疏介质,且光疏介质的折射率远远小于光密介质的折射率.n21=1表示光在一种介质中传播,或者从一种介质射向另一种折射率相同的介质.n21=+∞表示光由光疏介质射向光密介质,且光疏介质的折射率远远小于光密介质的折射率. 图3中6条边界线(a—f)和2条分界线(g,h),将图划分为3个区域(I—III). 下面对图3进行详细说明.

图3 反射光和入射光垂直于入射面的电场分量相位差的n21-θ空间分布图

图4 以布儒斯特角入射时反射光偏振示意图












图6 不同相对折射率下反射光和入射光垂直于入射面的电场分量相位差随入射角变化曲线
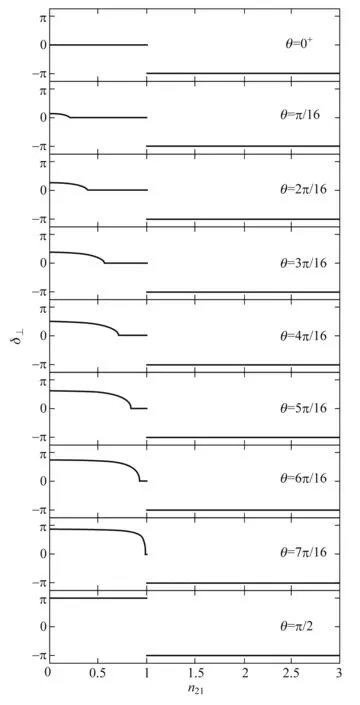
图7 不同入射角时反射光和入射光垂直于入射面的电场分量相位差随相对折射率变化曲线
为方便查阅,图3的相关内容可制成表1.
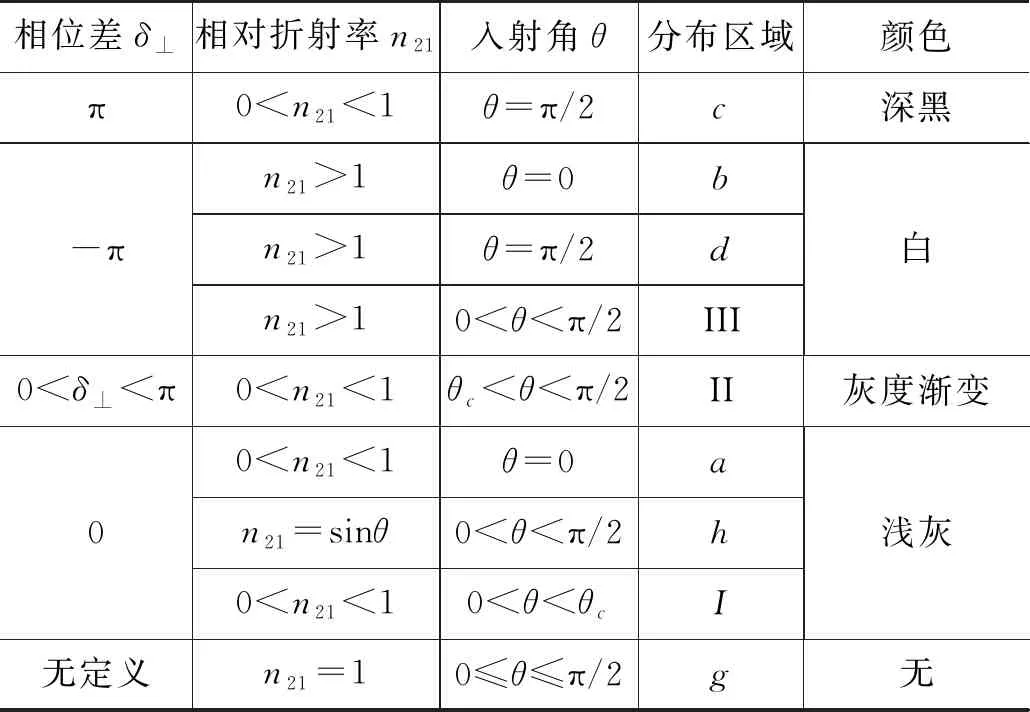
表1 垂直相位差δ⊥的n21-θ空间分布与标识颜色
图5中6条边界线(a—f)和3条分界线(g—i),将图划分为5个区域(I—V). 注意到图5比图3多一条分界线h,其原因是:在入射角为布儒斯特角时反射光的垂直电场分量并不会为零,也即在入射角大于和小于布儒斯特角的两种情况下,反射光的垂直电场分量方向并没有不同,这与反射光的平行电场分量性质不同. 下面对图5进行详细说明.
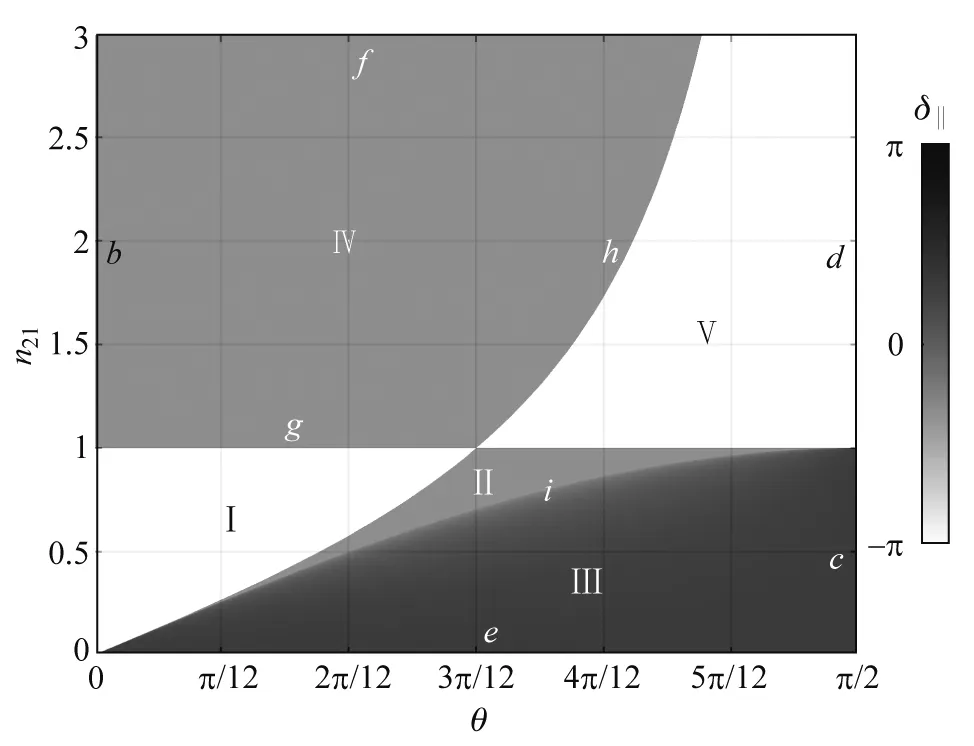
图5 反射光和入射光平行于入射面的电场分量相位差的n21-θ空间分布图



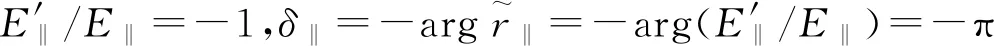

图9 不同入射角时反射光和入射光平行于入射面的电场分量相位差随相对折射率变化曲线


图8 不同相对折射率下反射光和入射光平行于入射面的电场分量相位差随入射角变化曲线



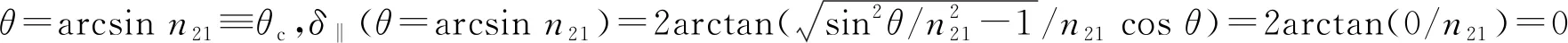
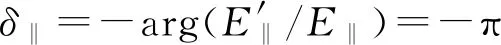
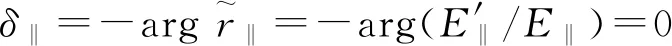




表2 平行相位差δ‖的n21-θ空间分布与标识颜色
2 讨论和结论
本文给出了详尽的两种非铁磁质的一般正折射率介质界面上反射光与入射光电场分量相位差的n21-θ空间分布图(图3和图5),详细给出了反射光发生半波损失的所有情况和条件(表1和表2). 在《中国中学教学百科全书·物理卷》“半波损失”词条中,对相位突变现象、洛埃镜实验和维纳光驻波实验做了说明和解释. 根据上述结果,可对其中的一些问题作出讨论:
1)本文研究发现:在洛埃镜干涉实验中,无论是光的平行电场分量还是垂直电场分量,以及无论光是由光疏介质射向光密介质,还是由光密介质射向光疏介质,都会发生相位差π的现象,见图3中线段c和d及图5中线段c和d. 因此,文献[2]在提到掠入射时界面处的反射光与入射光的电矢量振动方向相反时,不需要加上“光疏介质入射到光密介质”这个条件.
2)在维纳实验中,一定是光从光疏介质射向光密介质才会发生光驻波现象,因为只有此时电场分量是反向的,见图3和图5中的线段b. 这里需说明的是,图5中线段b虽然表示光从光疏介质垂直于分界面射向光密介质,在界面处发生反射,反射光和入射光的平行于入射面的电场分量不发生反相[指反射光平行电场分量的方向与图2(b)中E′所指方向相同],但是从图2(b)可以看出,当入射角为0时,反射光和入射光的平行于入射面的电场分量虽然不发生反相,但反射光和入射光的平行于入射面的电场分量方向是相反的. 这样就非常合理,因为正入射可以看作是光的电场分量垂直于入射面,也可以看作是光的电场分量平行于入射面,按这两种情形来讨论,理论上应给出相同的结果. 但由于反射光电矢量正方向的选择(见图2及引言部分的说明),数学上看上去结果不同(一个相位差π,一个没有相位差),但物理上都表示反射光和入射光的电场分量方向相反.
3)文献[2]原文提到“界面处的反射光与入射光的电矢量振动方向相反. 这表明两个光振动的位相差π,折算成光程,相当于有半个波长的光程差,故称这种现象为半波损失”,其实反射光与入射光的电矢量振动方向相反,并不一定是两个光振动的相位差π,这与光的电矢量振动的正方向的选取有关. 比如选取图2(b)中电矢量方向为正,从图5中线段b可知,光从光疏介质垂直于分界面射向光密介质,在界面处发生反射,反射光和入射光的电矢量方向相反,但反射光和入射光的相位差为零.我们也可以规定正方向为相反方向,但正如引言中已提到的,本文仍采用图2中正方向的规定是因为利多于弊.
4)文献[2]原文提到“还可证明两个结论. ①光从光密介质入射到光疏介质时,在非掠入射的情况下,反射光相对于入射光无半波损失”,其实如果半波损失根据“反射光和入射光相位差π”来定义,那么文献里漏了一种情况,即光由光密介质射向光疏介质且光疏介质的折射率远远小于光密介质的折射率,在界面处发生反射,反射光和入射光的平行于入射面的电场分量相位差π,见图5线段e.
半波损失是物理中一个重要的概念和知识点,它通常作为用于验证光的电磁理论正确性的一个例子,同时在涉及波的相干叠加问题[4]时需要对它特别加以考虑. 我们的研究进一步验证了电磁场理论的正确性,澄清和补充了一些现有教科书和科普读物中不很明确的结论,将有助于加强人们对麦克斯韦电磁理论的信心和认同,同时激发同学们对包含麦克斯韦方程的更宏大统一场理论的兴趣,有助于大学物理知识的讲学、传承和发扬.
致谢:感谢袁尤龙、朱宇晴、彭行坤、张鸿辉、陈江村、蔡奇龙、吴胜发等同学参与制图和讨论.

