采用GJ-型扣件地铁轨道的钢轨波磨形成机理
周志军,李 伟,温泽峰,朱强强,罗易飞
(1.西南交通大学 牵引动力国家重点实验室,四川 成都 610031;2.武汉地铁运营有限公司,湖北 武汉 430032)
随着我国地铁运营里程的不断增加,列车运行诱发的轮轨振动和噪声问题愈被关注,采用减振扣件(如科隆蛋,Vanguard,Lord和GJ-Ⅲ型扣件)取得了理想的减振降噪效果,但轮轨周期性磨耗(钢轨波磨、车轮不圆)也逐渐涌现。GJ-Ⅲ型扣件又称双层非线性减振扣件,属中等减振扣件,垂向静刚度为10~20 kN·mm−1,相比普通扣件减振效果可达10 dB[1],在学校和古建筑物等特殊减振地段被大量铺设。采用GJ-Ⅲ型扣件地铁轨道(简称GJ-Ⅲ型扣件轨道)运营一段时间后出现了短波长波磨,列车通过该波磨区段时易激励起轮轨系统高频振动,增大轮轨振动和噪声,导致车辆轨道部件过早疲劳失效,威胁列车运行安全。
钢轨波磨是轮轨系统动力学和磨耗损伤耦合的结果,波磨形成机理涉及众多因素,各因素间交互影响,诱发的波磨特征不同,形成机理也不具有普遍性,针对特定轨道特定条件的波磨形成机理需特定分析。金学松等[2]将波磨形成机理的动力类成因归纳为自激振动理论[3−5]和反馈振动理论[6−10]。前一理论认为波磨主要与车辆/轨道系统的固有特性相关;后一理论认为波磨是由轮轨初始不平顺(隐伤[11]、焊接接头[12]、非金属夹杂[13]) 引起,是“不平顺-振动-不平顺”的循环过程。Jin等[14]通过对我国地铁钢轨波磨的现场试验、长期跟踪观察和数值分析,验证了波磨的形成与车辆/轨道系统固有特性相关,尤其是轨道结构的动态特性,如线路中焊接接头等缺陷激励的轨道结构敏感共振特性不同,从而诱发的波磨波长不同。针对短波长波磨,Grassie[15]研究表明其形成主要由钢轨Pinned-Pinned共振所致,是频率固定机制,但我国地铁列车速度普遍较低,最高仅达160 km·h−1,GJ-Ⅲ型扣件轨道短波长波磨(波长为40~50 mm)导致的通过频率还达不到钢轨Pinned-Pinned共振的高频率(在钢轨类型为60 kg m−1和轨枕间距为625 mm条件下,约为 1 000~1 200 Hz[16])。此外,P2共振频率50~100 Hz[17]和轨枕通过频率250~400 Hz[18]相对较低,不是导致形成GJ-Ⅲ型扣件轨道的短波长波磨机理。
为研究更高频率(400~1 000 Hz)范围的波磨形成机理,现阶段开发的波磨分析模型除线性模型[6−7,19−20]外,还有非线性模型[21−26]和非稳态模型[27−28]。李伟等[29]基于波磨线性模型和力锤敲击试验,表明GJ-Ⅲ型扣件在620~840 Hz高频段的轨道垂向位移导纳低,导致钢轨磨损率低,进而诱发了30~40 mm短波长波磨,但线性模型仅能从频域角度定性分析波磨萌生特征和速率。采用车辆-轨道耦合动力学方法,基于静力学的Hertz/非Hertz理论求解法向接触和Kalker理论求解切向接触问题时,对处理轮轨动态相互作用引起的非稳态过程有很大局限性[30],且不能很好地考虑轮轨结构高频柔性。有限元法可以考虑详尽的轮轨系统动力学、接触力学、损伤之间的相互耦合作用,这是解释波磨形成机理的关键。虽然Vo等[31]、Lu等[32]、Ma等[33]利用有限元法分析了轮轨静态和动态接触力或应力,于淼[34]、Zhao 等[35]分析了钢轨不平顺激励的非稳态接触力,但是对于轮轨固有特性和轨道初始不平顺共同诱发的钢轨非均匀磨耗还缺乏深究,尤其短波长波磨形成机理仍不够清楚。
本文针对调研和测试的我国8条地铁线路GJ-Ⅲ型扣件轨道中钢轨普遍出现的短波长波磨特征,建立考虑轮轨结构高频柔性、真实接触几何、材料连续体振动、轮轨滚滑与瞬态冲击等多因素的地铁三维轮轨滚动接触有限元模型,频域内分析钢轨焊接接头短波长凹陷(简称钢轨短波长凹陷)激励下的轮轨高频非稳态接触力,时域内再现轮轨瞬态滚滑行为和钢轨纵向磨耗特征,基于结构动力学和磨耗损伤解释GJ-Ⅲ型扣件轨道钢轨波磨形成机理。
1 GJ-Ⅲ型扣件轨道的钢轨波磨特征
典型的GJ-Ⅲ型扣件轨道钢轨短波长波磨如图1所示。图中:v为车辆运行速度;λ为波磨的波长。

图1 GJ-型扣件轨道的钢轨波磨
轨道结构及其参数(如轨枕间距,扣件刚度和阻尼,线路类型和轨道减振措施)、车辆结构及其参数(如轮对,轴重和簧下质量)、轮轨耦合作用及其运行环境(如速度,牵引/制动和润滑)对钢轨波磨形成具有直接或间接的影响。因此,现场调查和测试了我国8条地铁线路(线路A—线路H)的GJ-Ⅲ型扣件轨道不平顺特征,如图2所示。图中:轨道不平顺的波长进行了20~300 mm滤波处理,且为1/3倍频程中心波长;限值为标准ISO 3095—2013《声学轨道车辆外部噪声测量》规定的轨道不平顺限值;R为曲线半径;钢轨不平顺水平为
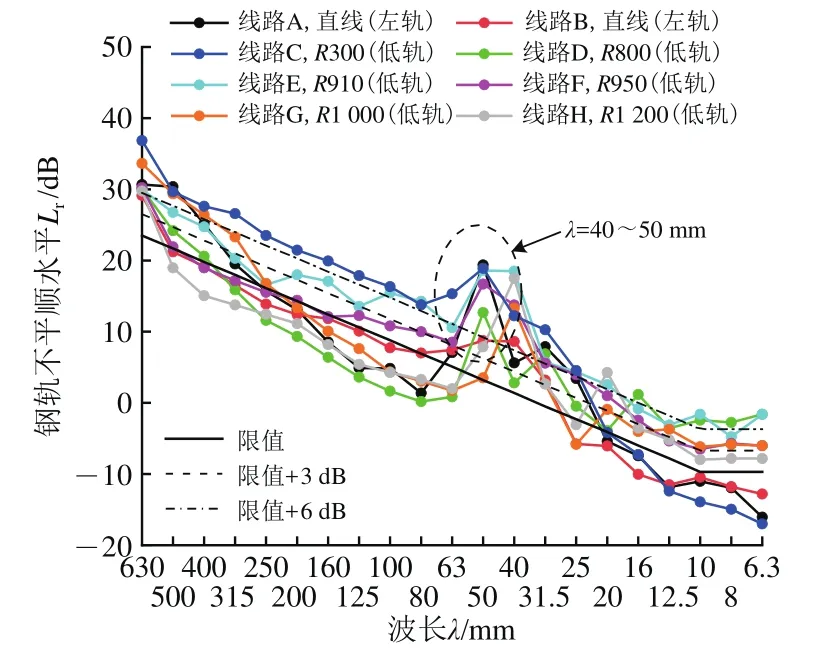
图2 GJ-型扣件轨道的钢轨不平顺特征

式中:Lr为钢轨不平顺水平,dB;rRMS为钢轨不平顺均方根值,μm;r0为不平顺参考基准值,取r0=1 μm。
图2中GJ-Ⅲ型扣件轨道的波磨特征及其对应的不同线路参数和车辆参数见表1。
表1 GJ-型扣件轨道的波磨特征及其对应的不同线路参数和车辆参数
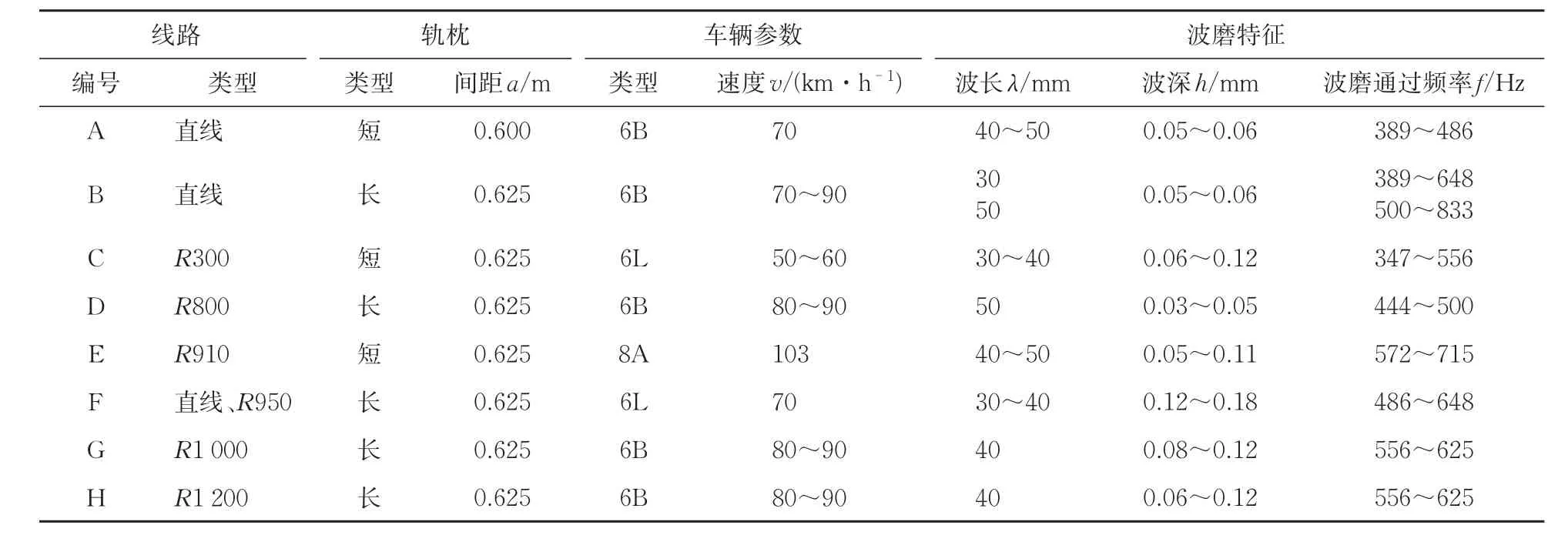
表1 GJ-型扣件轨道的波磨特征及其对应的不同线路参数和车辆参数
线路编号轨枕类型波磨特征间距a/m车辆参数类型类型速度v/(k m·h-1)波长λ/m m 波深h/m m 波磨通过频率f/H z 0.6 0 0 0.6 2 5 0.6 2 5 0.6 2 5 0.6 2 5 0.6 2 5 0.6 2 5 0.6 2 5 6 B 6 B 6 L 6 B 8 A 6 L 6 B 6 B A B C D E F G H直线直线R 3 0 0 R 8 0 0 R 9 1 0直线、R 9 5 0 R 1 0 0 0 R 1 2 0 0短 长 短长短长长长7 0 7 0~9 0 5 0~6 0 8 0~9 0 1 0 3 7 0 8 0~9 0 8 0~9 0 4 0~5 0 3 0 5 0 3 0~4 0 5 0 4 0~5 0 3 0~4 0 4 0 4 0 0.0 5~0.0 6 0.0 5~0.0 6 0.0 6~0.1 2 0.0 3~0.0 5 0.0 5~0.1 1 0.1 2~0.1 8 0.0 8~0.1 2 0.0 6~0.1 2 3 8 9~4 8 6 3 8 9~6 4 8 5 0 0~8 3 3 3 4 7~5 5 6 4 4 4~5 0 0 5 7 2~7 1 5 4 8 6~6 4 8 5 5 6~6 2 5 5 5 6~6 2 5
表1中波磨通过频率为

式中:f为波磨通过频率,Hz。
由图2和表1可知如下结果。
(1)因线路A—线路H的轨道和车辆参数不一致,GJ-Ⅲ型扣件轨道的波磨特征不唯一,波长表现为30~50 mm,该波长为短波长波磨[15],波深为0.03~0.18 mm。车辆在不同线路上运行时速度很难保持统一(50~103 km·h−1),导致波磨通过频率的范围(347~833 Hz)较广。
(2)当相同类型(6B)的车辆以相同速度(80~90 km·h−1)运行在轨枕间距和类型相同的线路D、线路G和线路H时,不同线路(R800、R1 000和R1 200)会诱发不同波长(40或50 mm)的波磨,这表明波磨的形成与曲线线路半径有关。
(3)当不同类型(6B和6L)的车辆以相同的速度(70 km·h−1)运行在轨枕间距和类型相同的线路B和线路F时,相同线路类型(直线)会诱发相同波长(30 mm)的波磨,这表明波磨的形成与车辆类型无关。
(4)当不同类型(6L和8A)的车辆以不同的速度(50~60和103 km·h−1)运行在轨枕间距和类型相同的线路C和线路E时,不同线路(R300和R910)会诱发不同波长(30~40和40~50 mm)的波磨,这表明列车运行速度和曲线线路半径共同诱发了不同波长波磨。
(5)当相同类型(6B)的车辆以相同的速度(70 km·h−1)运行在轨枕间距和类型不同的线路A和线路B时,相同线路类型(直线)会诱发不同波长(30,50和40~50 mm)的波磨,这表明波磨的形成与轨枕类型和间距有关。
因此,根据现场调研和测试结果来看,GJ-Ⅲ型扣件轨道钢轨波磨的形成很大程度与轨道结构(包括线路类型及轨枕类型和间距)相关,不确定是否与列车运行速度相关,还需借助有限元模型进行深入分析其根源。
2 考虑钢轨短波长凹陷激励的三维轮轨滚动接触有限元模型
2.1 三维轮轨滚动接触模型
利用ABAQUS商业软件,采用隐-显式算法相结合的方式,建立GJ-Ⅲ型扣件轨道的三维轮轨滚动接触有限元模型。鉴于波磨的短波长特性,波磨波长约为轨枕间距的6%~8%,故忽略线路曲率的影响[36],模拟车轮在直线轨道滚动。该模型集成车辆-轨道结构高频柔性、真实接触几何、材料连续体振动、轮轨蠕滑与瞬态冲击等因素,包含簧上质量、一系悬挂、车轮、钢轨、扣件和道床板为一体的车辆-轨道系统[36]。车辆-轨道系统沿线路中心线具有对称性,故该模型仅取一半。模型参数见表2。
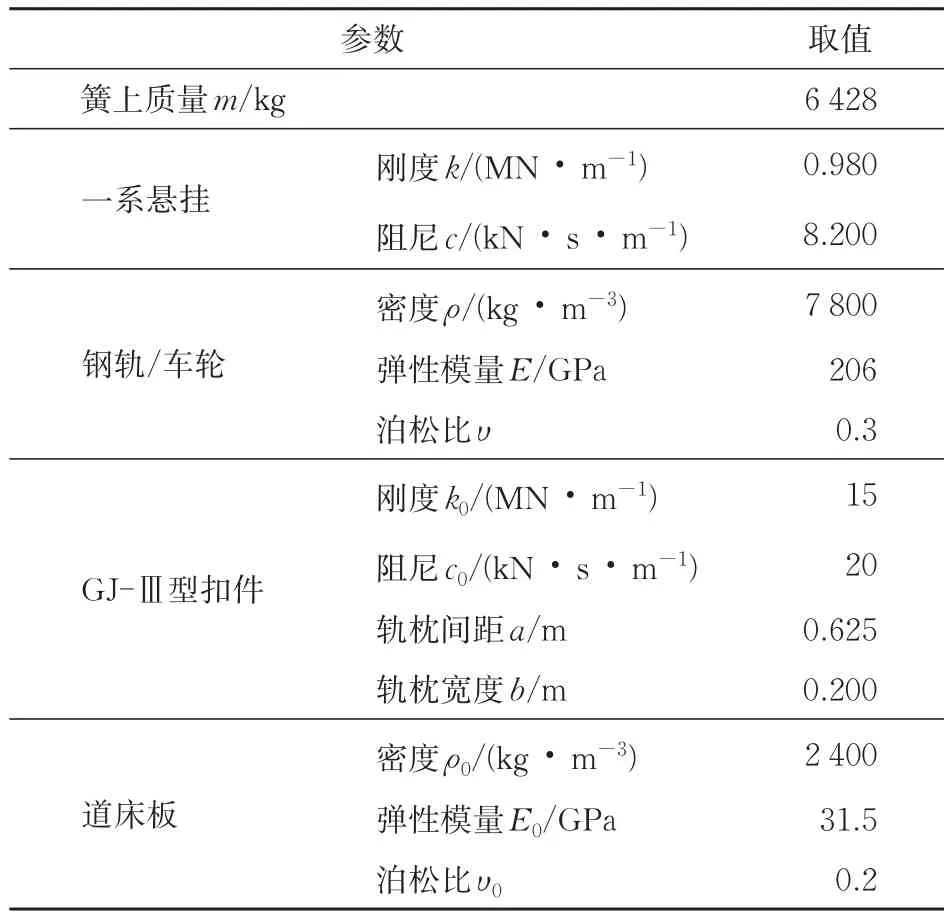
表2 三维轮轨滚动接触有限元模型参数
为模拟车轮通过钢轨短波长凹陷激励时的轮轨接触响应,建立模型时考虑无磨耗车轮在直线短波长凹陷钢轨上的滚滑行为。车轮初始位置位于轨枕上方,无侧滚和冲角,轮轨对中接触。车轮型面为LM,钢轨型面为CN60,轨底坡为1/40,轨距1 435 mm。轮轨空间运动和材料变形采用Lagrang⁃ian方法描述,车轮、钢轨和道床板实体结构采用八节点六面体线性缩减积分单元(C3D8R)进行离散,并以增强应变方法控制单元本身沙漏模态缺陷问题,实体结构仅考虑为线弹性材料。一系悬挂和扣件均由离散的弹簧和阻尼单元模拟,每组扣件由12个弹簧-阻尼单元沿纵向离散支撑(共20组,240个),一系悬挂由4组弹簧-阻尼单元连接簧上质量与车轴中心,并施加耦合约束确保其滚动和平动位移运动一致性[34]。
轮轨滚动示意图如图3所示。图中:M0为牵引扭矩;ω为车轮滚动角速度。经试算,轨道模型全长L为12.5 m时,可避免边界效应带来的误差,足以解决波磨波长和频率问题[28,34,36−37]。首先,设静态接触区(AB段,L1=20 mm),采用隐式法求解轮轨初始静态时的接触斑形状和接触压力;然后,考虑将静态接触解导入显式模型中求解轮轨瞬态滚动时会引入较大的初始激扰,因此设动态松弛区 (BC段,L2=2.4 m[34,36]),使初始激扰的轮轨系统振动衰减达到稳态;最后,设短波长凹陷区(CD段,L30+L3=1 m,L30=100 mm),求解轮轨瞬态滚动接触,分析钢轨波磨形成机理。
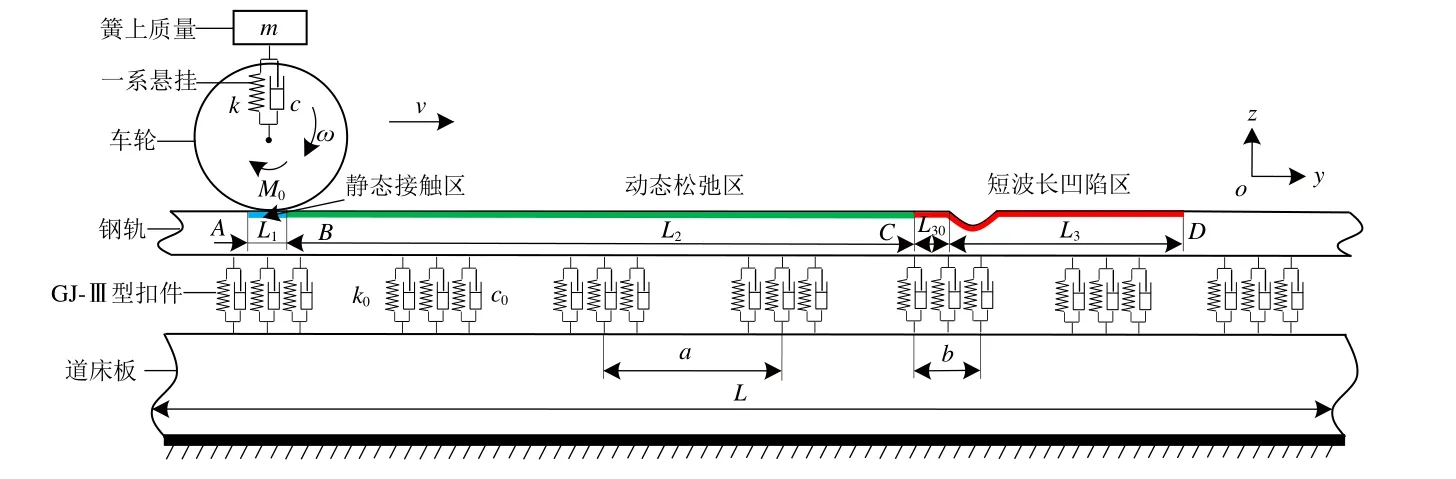
图3 轮轨滚动示意图
为协调模型规模与计算精度和效率之间的最大平衡,静态接触区和短波长凹陷区内的轮轨接触单元尺寸为(1×1) mm,其他区域进行过渡稀疏网格划分[34,36],得到GJ-Ⅲ型扣件轨道的三维轮轨滚动接触有限元模型局部图如图4所示。模型总计150.1万个单元数和171.4万个节点数。在模型中建立笛卡尔坐标系oxyz以表达轮轨滚动时的相对位置(如图3、图4所示)。采用显式算法求解轮轨瞬态滚动时模型边界条件如下:钢轨和道床板的纵断面沿y纵向对称约束,车轮端面沿x横向约束,车轮中心面沿x横向对称约束,一系质量点保留垂向z和纵向y的平动。
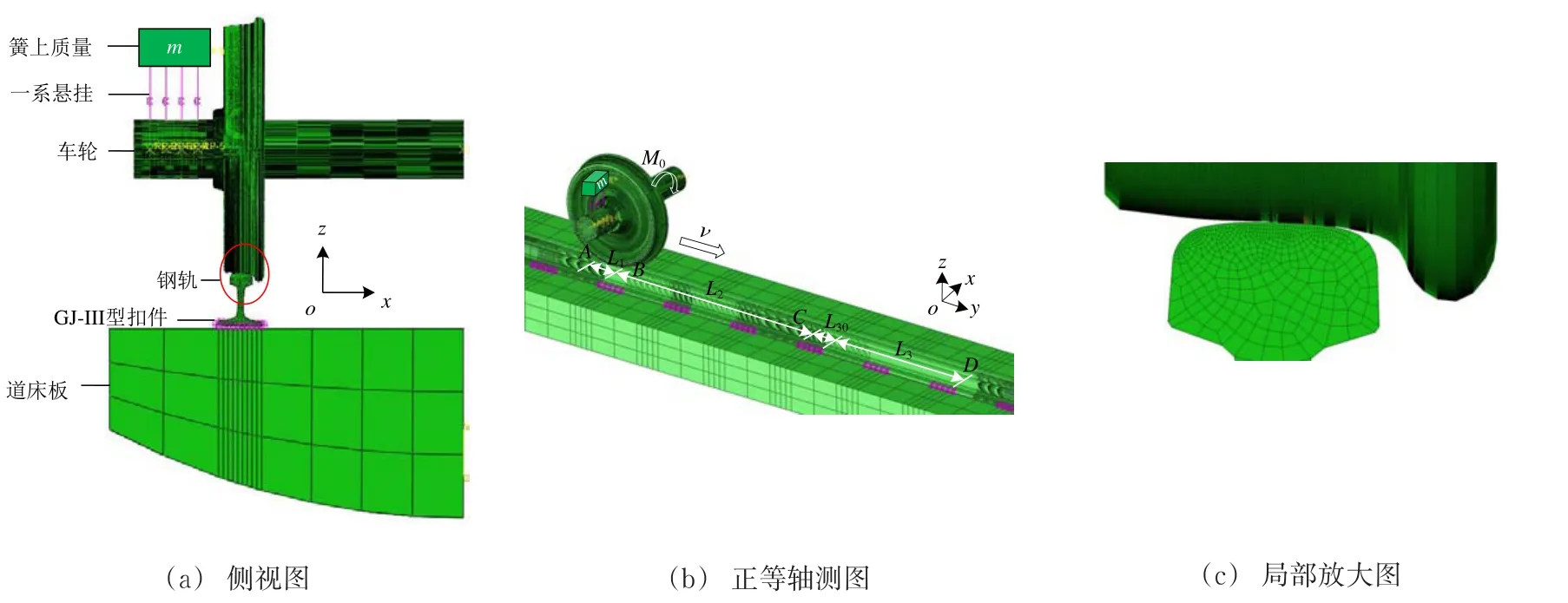
图4 GJ-型扣件轨道的三维轮轨滚动接触有限元模型局部图
轮轨接触基于“面-面”接触算法,采用有限滑移可以防止主从接触面相对滑移量过大(大于特征单元尺寸的20%),减小计算误差。法向接触采用“硬”接触,切向接触采用“罚”函数法,摩擦系数μ'为 0.5[34,36]。轮轨瞬态滚动时设定车轮的平动速度、转动角速度和一系悬挂簧上质量点平动速度,同时施加牵引扭矩模拟车轮牵引工况。在有限元模型中车轮牵引扭矩的施加方式如图5所示。图中:r为车轴半径;P1—P4为车轴表面的4个等分点;P0和Q分别为车轴两边端面的中心点;t和t0分别为分析步时间和开始达到最大牵引扭矩时的分析步时间,t0=0.02 s。

图5 车轮牵引扭矩的施加
牵引扭矩M0和牵引系数μ分别为

式中:FN和FL为轮轨法向力和轮轨切向力,kN;r0为车轮名义滚动圆半径,mm;
2.2 钢轨短波长凹陷模型
为激励轮轨高频振动,施加钢轨短波长凹陷以模拟钢轨焊接接头凹陷,具体操作是根据短波长凹陷的凹陷深度修改轨头表面局部节点坐标进行施加,凹陷纵向为余弦函数分布,横向为抛物线函数分布。凹陷深度为
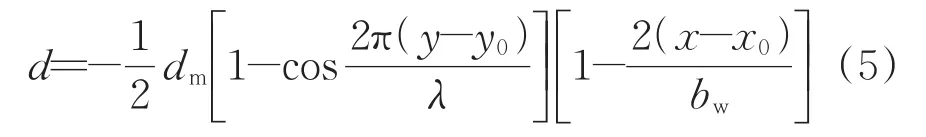
式中:d为凹陷深度,mm;dm为凹陷最大深度,mm;y为钢轨纵向坐标,mm;y0为凹陷纵向初始坐标,mm;bW为凹陷横向宽度,mm;x为钢轨横向坐标,mm;x0为轮轨接触斑中心横向坐标,mm。
不同波长凹陷的激励频率不同,从而诱发的轮轨系统动力学和接触力学响应特征是波磨形成机理的关键。因此,在图3、图4(b)所示的C点之后L30=100 mm位置处,施加波长分别为25,30,40,50,60,70,80和90 mm、深度为0.1 mm的短波长凹陷,不同波长凹陷的纵向几何形状如图6所示。

图6 钢轨短波长凹陷的纵向几何形状
钢轨施加短波长凹陷后网格节点发生位移,需要保证凹陷深度小于该区域钢轨单元特征尺寸(1 mm)的15%,以免对轮轨瞬态滚动接触行为产生影响。以波长为25 mm、深度为0.1 mm为例,施加凹陷后的钢轨表面如图7所示。
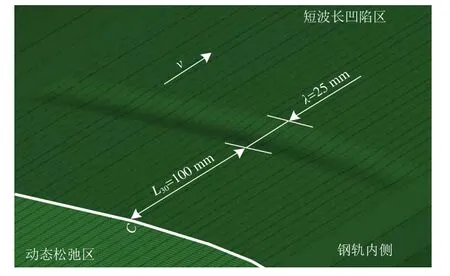
图7 施加短波长凹陷后的钢轨表面
2.3 钢轨Archard磨耗模型
为模拟轮轨高频共振诱发的钢轨纵向磨耗特征,利用钢轨Archard磨耗模型计算车轮滚过短波长凹陷后的钢轨纵向磨耗,即轮轨接触界面存在一定的蠕滑力而消耗能量造成的磨耗体积,为
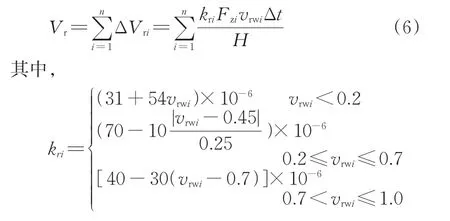
式中:Vr为钢轨轨头材料磨耗体积,m3;i为接触斑内任意单元;kr为无量纲的钢轨磨耗系数,与轮轨接触压应力和相对滑动速度有关[35];Fz为轮轨法向接触力,kN;vrw为轮轨接触斑内节点的相对滑动速度,m·s−1;Δt为磨耗计算时间步长,s;H为钢轨材料的维氏硬度,GPa。
2.4 模型可靠性验证
采用Hertz接触理论和Kalker的CONTACT数值程序及有限元模型,分别计算轮轨法向和切向接触应力分布,验证建立的三维轮轨滚动接触有限元模型(简称FEM)的可靠性。采用3种方法计算的轮轨法向接触应力和切向接触应力沿接触斑纵向分布结果,如图8所示。
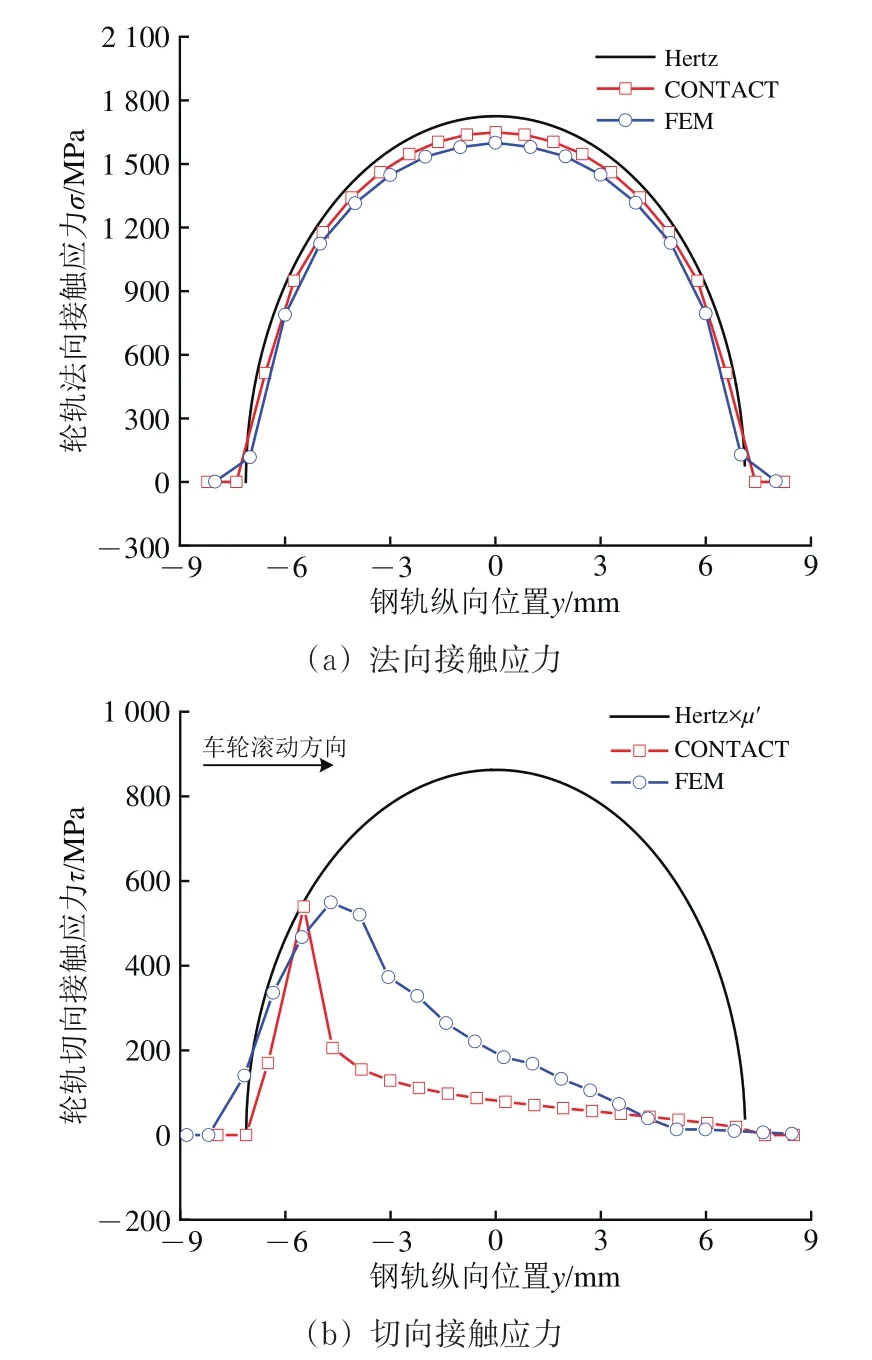
图8 轮轨接触应力二维分布
由图8可知:3种方法计算的轮轨接触斑形状尺寸基本一致,CONTACT数值程序和FEM计算的轮轨法向接触应力略小于Hertz接触理论;3种方法计算的接触斑后沿滑动区的切向接触应力结果差异较小,FEM计算的前沿黏着区的切向接触应力大于CONTACT数值程序,这是由于FEM计算时考虑了轮轨结构的柔性和较软的扣件刚度阻尼,轮轨接触弹性变形较大所致。因此,基于轮轨接触应力角度,建立的有限元模型求解轮轨接触特性是可靠的。
3 轮轨高频振动特性
车轮以速度为103 km·h−1、牵引系数为0滚过动态松弛区(L2)和短波长凹陷区(L3)时,轮轨力变化过程如图9所示。
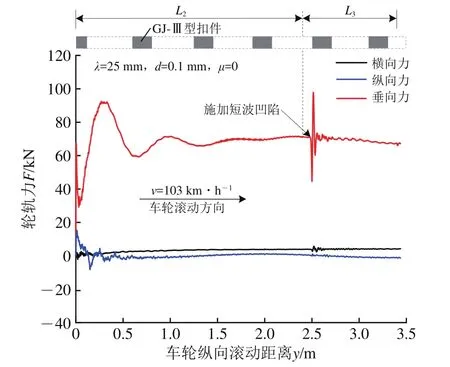
图9 动态松弛区和短波长凹陷区的轮轨力变化过程
由图9可知:时域内轮轨力整体呈现初始激扰—稳态滚动—瞬态冲击—逐渐衰减的过程;动态松弛区(L2)内轮轨力曲线变化趋势与Vo等[31]、于淼[34]的研究相似,也基于轮轨力的角度验证了模型的可靠性;当车轮正好通过动态松弛区(L2)后,即车轮纵向滚动距离为2.4 m时,轮轨垂向力为70.8 kN,相比轴重7 t的静轮重68.67 kN增大约3.1%,误差较小;若钢轨足够长,则经过更长的动态松弛区后轮轨力将接近于轮轨静态力。为了均衡计算成本和效率问题,认为车轮以速度103 km·h−1通过长度L2为2.4 m[34,36]的动态松弛区时轮轨力达到了稳态,满足本文计算需求,可以进行钢轨短波长凹陷瞬态冲击分析。此外,因三维轮轨瞬态滚动接触有限元模型中忽略了轮对横向运动,故轮轨横向力趋于0。
因为在建立的直线段三维轮轨滚动接触有限元模型中,轮轨系统振动主要在垂向上占优,车轮以103 km·h−1速度通过波长为 20,25,30,40,50,60,70,80和90 mm的短波长凹陷钢轨时,激励的轮轨垂向力如图10所示,不同波长凹陷的激励频率与轮轨垂向力频率的关系见表3。
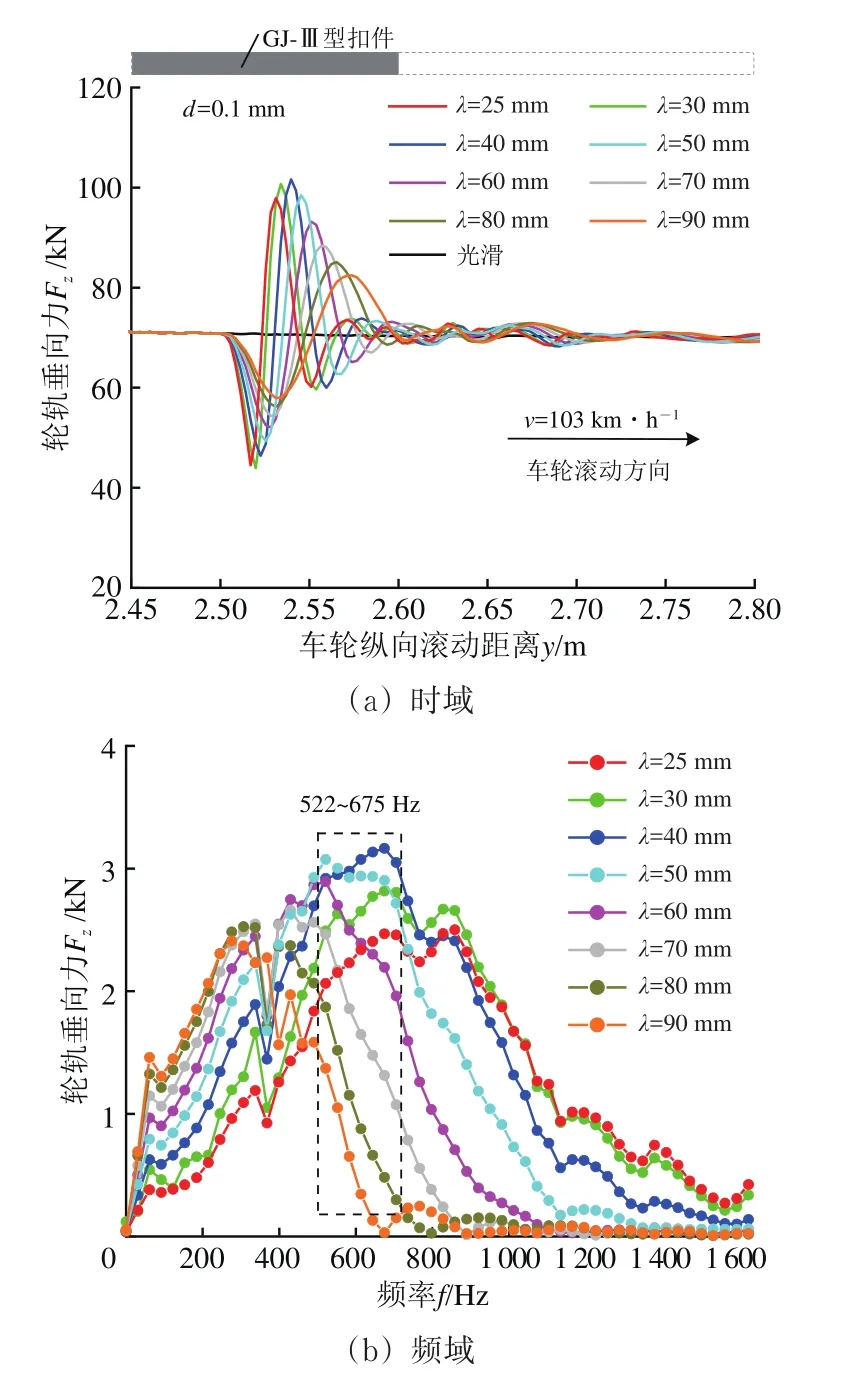
图10 不同波长短波长凹陷激励的轮轨垂向力
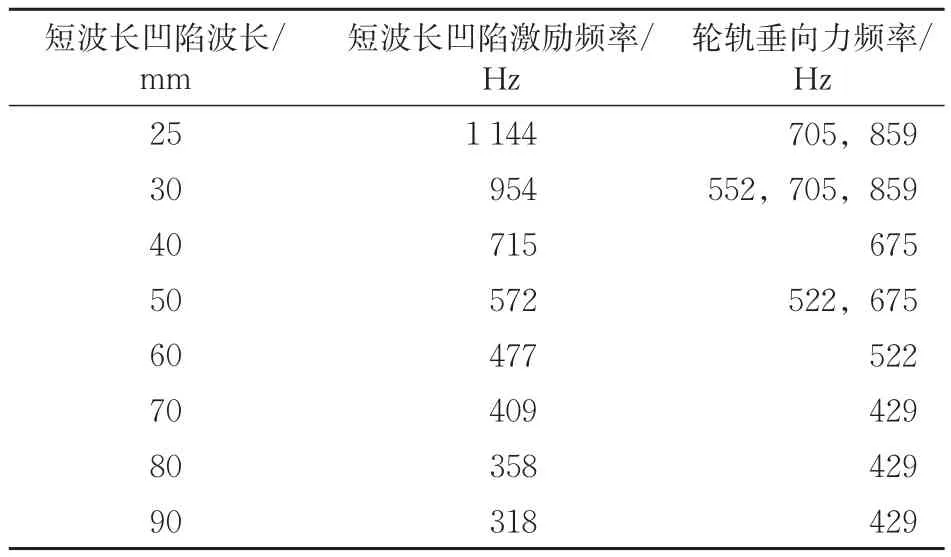
表3 不同波长短波长凹陷的激励频率与轮轨垂向力频率的关系
由图10可知:相同短波长凹陷波深和车速下,时域内轮轨垂向力最大值并非随短波长凹陷波长的增大而增大,而是短波长凹陷波长为40 mm时最大,90 mm时最小;短波长凹陷波长为25~90 mm时的激励频率为311~1 144 Hz,范围较宽,其中短波长凹陷波长为70~90 mm时激励频率较低,导致轮轨垂向力频率仅为429 Hz,所以波长为70~90 mm时的短波长凹陷激励不起与波磨通过频率572~715 Hz相关的轨轮系统高频振动特性;当短波长凹陷波长为25~60 mm时激励频率较高,导致轮轨垂向力显著频率为522~675 Hz,其中波长为40 mm时轮轨垂向力最大。
因此,考虑GJ-Ⅲ型扣件轨道的轮轨系统对于波长为40 mm的短波长凹陷激励响应最敏感,当列车以103 km·h−1速度通过该轨道时容易激励起522~675 Hz的轮轨系统共振,诱发波长为42~54 mm的波磨萌生,这与表1中线路E的钢轨波磨特征相符。
为分析表1中不同速度下的钢轨波磨特征相对差异,车轮以75,85,95和103 km·h−1速度通过波长为25 mm、波深为0.1 mm的短波长凹陷时激励的轮轨垂向力如图11所示。
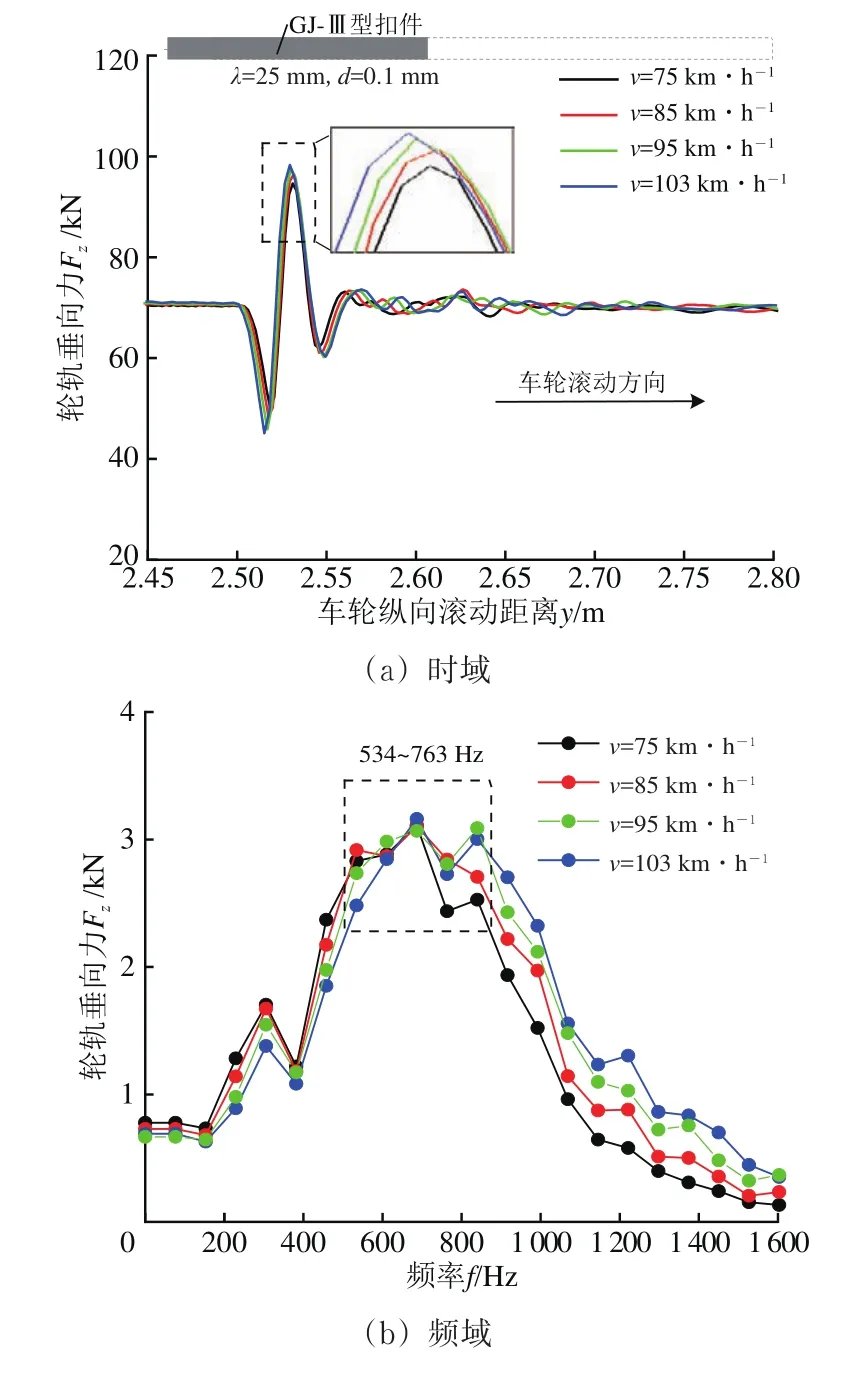
图11 车轮不同滚动速度激励的轮轨垂向力
由图11可知:时域内轮轨垂向力最大值随车速的增大而增大,而相位滞后;频域内车速轮轨垂向力显著频率不随车速的变化而改变,恒定频率为534~763 Hz,中心频率为687 Hz,该恒定频率与图10中相同车速不同短波长凹陷波长激励的轮轨垂向力频率(522~675 Hz)接近。
综上所述,轮轨系统在不同钢轨短波长凹陷和车速激励下的轮轨垂向力显著频率为522~763 Hz,这与波长为40~50 mm波磨的通过频率572~715 Hz比较吻合,表明GJ-Ⅲ型扣件轨道的钢轨波磨产生是列车通过线路时由诸如钢轨焊接接头凹陷等短波不平顺激发的轮轨高频动态特性被诱发所致。此外,根据现场调查结果发现,车辆以103 km·h−1速度运行在具有短波长波磨的GJ-Ⅲ型扣件轨道时,因为短波长波磨导致扣件断裂的现象频有发生,临时采取降速至75 km·h−1处理后,虽降低了约4%的轮轨垂向力,但并不能改变轮轨系统的显著共振频率,亦不能明显缓解钢轨波磨的发展。
4 钢轨波磨形成机理和磨耗特征
4.1 车轮-轨道固有特性
为探明上述轮轨力显著频率的来源,基于可考虑轮轨接触非线性特性的子空间方法提取车轮-轨道耦合模态,分析与波长为40~50 mm波磨通过频率相关的车轮-轨道耦合固有特性。模态分析结果表明,在100~430 Hz频率范围内车轮-轨道耦合模态振型均表现为以车轮的弯曲或扭转振动为主,而在520~750 Hz较高频率范围内均表现为以钢轨垂向弯曲振动为主,主要频率有520,555,569,597,641,673,712和748 Hz,其中569和673 Hz频率对应的车轮-轨道耦合模态振型如图12所示。
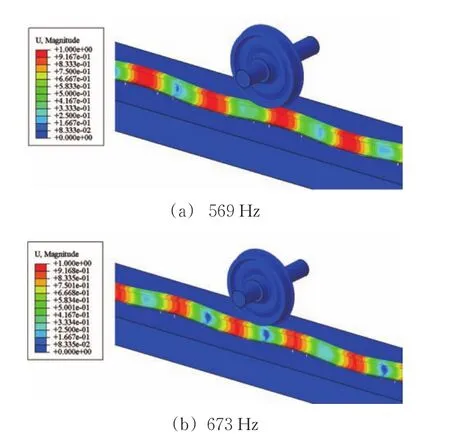
图12 以钢轨垂向弯曲振动为主的车轮-轨道耦合模态振型
为进一步解释在车轮-轨道耦合模态的显著频带内哪一确定频率占主导,借助现场力锤敲击法获得轨道结构(包括轨枕上方钢轨和跨中钢轨)频响特性如图13所示。图中:222 Hz为钢轨相对道床板的垂向弯曲振动频率,1 106 Hz为钢轨垂向1阶Pinned-Pinned共振频率。
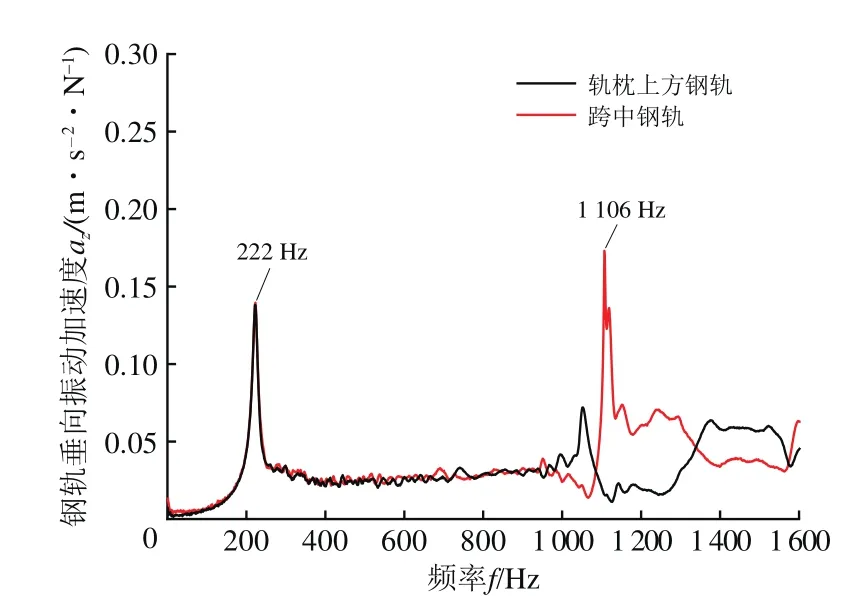
图13 力锤敲击获得的轨道结构频响特性
由图13可知:Pinned-Pinned共振频率与波磨通过频率(572~715 Hz)相差较远,故GJ-Ⅲ型扣件轨道钢轨波磨的产生不是因钢轨Pinned-Pinned共振所致。值得注意的是,轨道频响特性显示的2个频率最容易被激发,导致钢轨垂向振动加速度幅值较高,其他频率特性可能被覆盖。而且力锤敲击法是一种静态测试手段,相比真实轮轨瞬态冲击,力锤敲击能量较低,不足以激励起钢轨波磨通过频率相关的高频振动。
因此,在2.1节建立的轮轨静态接触模型基础上,未考虑簧下质量时,在轨枕上方钢轨轨头中心节点施加白噪声激励(在整个频域范围内所有频率都具有相同能量密度的随机激励,如图14(a)所示),得到与激励点距离为2.5 m(车辆轴距)、轨头中心节点处的钢轨垂向振动加速度响应如图14(b)所示。
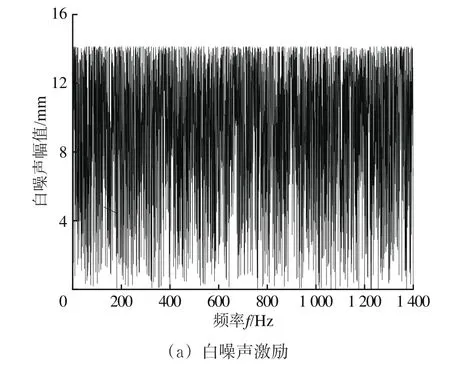
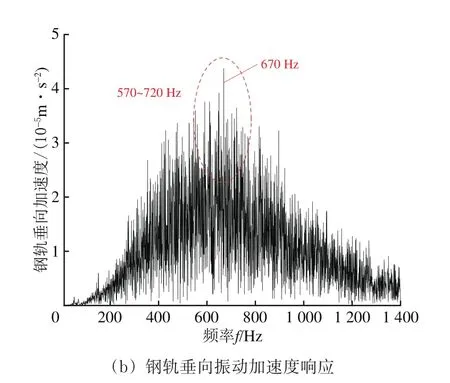
图14 白噪声激励与钢轨垂向振动加速度响应
由图14可知:在白噪声激励下,钢轨垂向振动加速度显著频率为570~720 Hz,最显著频率为670 Hz,该最显著频率与钢轨短波长凹陷激励下的轮轨垂向力频率522~763 Hz接近。
综上所述,GJ-Ⅲ型扣件轨道的轮轨系统显著振动频率主要与轨道结构的高频固有特性相关,其振型主要表现为钢轨相对道床板的垂向弯曲振动。若在钢轨短波长凹陷等激励下,易诱发轮轨系统高频振动,导致轮轨力波动,最终形成钢轨纵向不均匀磨耗。
4.2 钢轨纵向磨耗特征
利用考虑钢轨短波长凹陷激励的三维轮轨滚动接触有限元模型,计算车轮以不同滚动速度和牵引系数滚过短波长凹陷(波长为25 mm,波深为0.1 mm)后的轮轨力和接触斑内节点的相对滑移速度等参量,基于钢轨Archard磨耗模型计算钢轨纵向磨耗特征。
当车轮以75,85,95和103 km·h−1滚动速度通过短波长凹陷后,钢轨表面形成的磨耗量如图15所示。图中:钢轨磨耗量经过20~100 mm波长滤波。
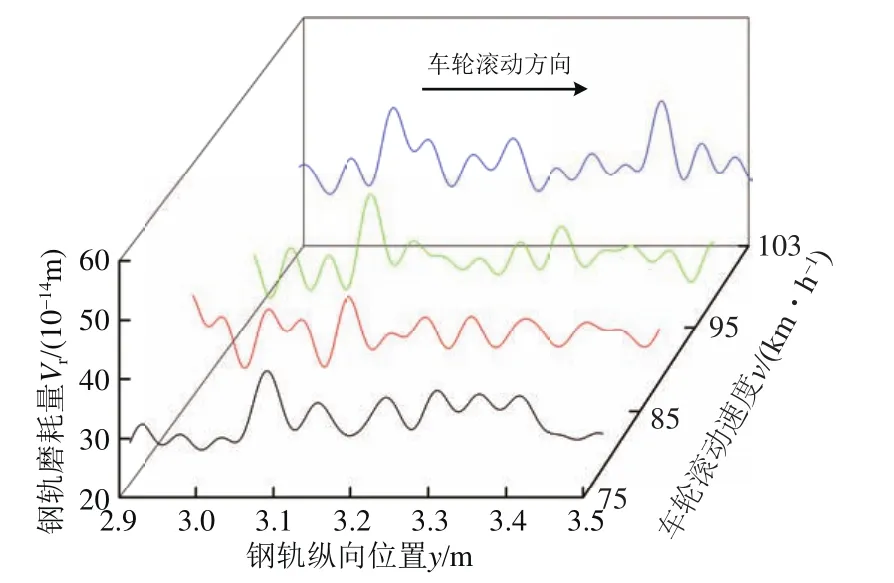
图15 不同车速下钢轨磨耗量沿钢轨纵向分布(μ=0.300)
由图15可知:车轮牵引系数为0.300,不同滚动速度滚过短波长凹陷后的钢轨磨耗沿纵向呈近似的周期分布,磨耗显著波长不唯一,且磨耗量随车速的增大而增大。
为体现显著波长的贡献,对时域内沿钢轨纵向位置分布的钢轨磨耗量结果进行1/3倍频程变换,得到不同车速下钢轨不平顺水平与波长之间的关系如图16所示。

图16 不同车速下钢轨不平顺水平与波长的关系(μ=0.300)
由图16可知:钢轨不平顺显著波长随车速的增大而增大,75,85,95,103 km·h−1滚动速度导致的钢轨不平顺显著波长分别为31.5,31.5和40,40,40和50 mm。这是因为车轮不同滚动速度导致的轮轨垂向力显著频率为534~763 Hz(如图11(b)所示),表现为恒定频率机制。根据波长、速度和频率之间的关系,若轮轨垂向力频率恒定不变,随着车速的增大,导致波磨波长也依次增大,这也印证了轮轨力波动导致钢轨磨耗同频率波动的事实。需要注意的是,75,85和103 km·h−1速度导致的钢轨不平顺显著波长分别与表1中线路B,线路G和H,线路E的钢轨波磨波长吻合。
因地铁列车启停频繁,考虑车轮牵引对轮轨力和钢轨磨耗的影响,车轮牵引系数为0,0.075,0.150和0.300下的轮轨力如图17所示。
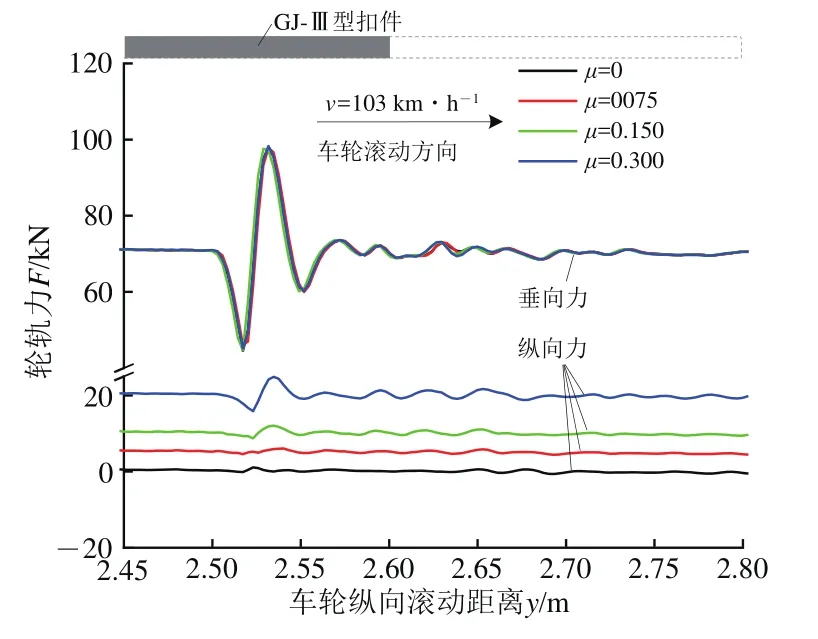
图17 不同牵引系数下的轮轨力
由图17可知:车速为103 km·h−1时,牵引系数对轮轨垂向力大小和相位无影响,瞬态和稳态的轮轨纵向力随牵引系数的增大而增大。
当车轮以0,0.075,0.150和0.300牵引系数通过短波长凹陷后,钢轨表面形成的磨耗量如图18所示。图中:钢轨磨耗量经过20~100 mm波长滤波。
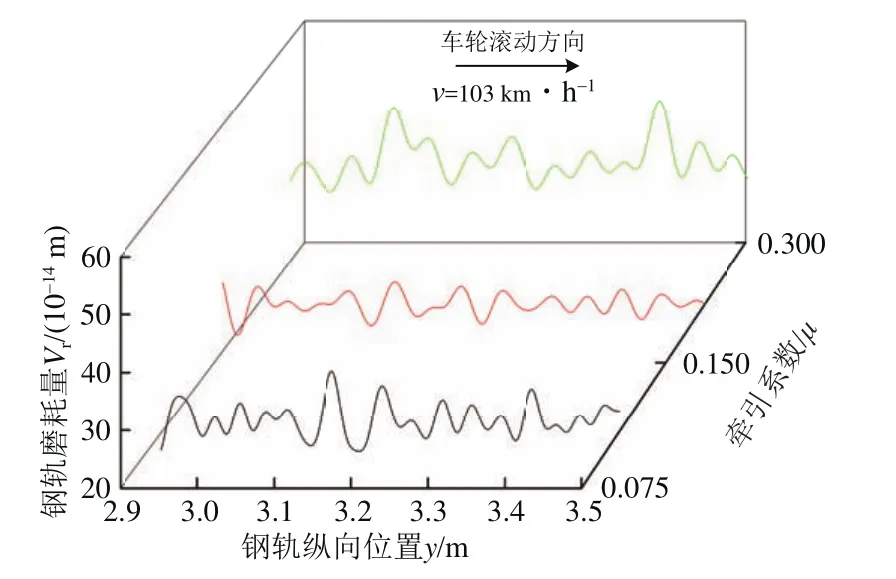
图18 不同牵引系数下的钢轨磨耗量沿钢轨纵向分布(μ=0.300)
对时域内沿钢轨纵向位置分布的钢轨磨耗量结果进行1/3倍频程变换,得到车轮不同滚动速度下钢轨不平顺水平与波长之间的关系,如图19所示。

图19 不同牵引系数下的钢轨磨耗水平与波长的关系(v=103 km·h-1)
由图18和图19可知,车轮不同牵引系数导致的钢轨不平顺显著波长分别为40,40和50,40和50 mm,该波长基本不随牵引系数的增大而增大。这是因为直线段轮轨系统振动主要在垂向占优,轮轨垂向力振动频率和车速才是决定波磨波长的主要原因[2],而牵引系数不影响轮轨垂向力大小,且3种牵引系数对应的车速相等,导致不同牵引系数诱发的钢轨磨耗波长基本为恒值。
应该强调,本文所建立的三维轮轨滚动接触有限元模型仅模拟车轮单次通过钢轨短波长凹陷的过程。仿真中,当车速为低速75 km·h−1时,诱发的磨耗显著波长仅为31.5 mm,这与现场调查的线路B中的双波长30 mm或者50 mm波磨不完全一致,略有差异。原因可能是:本文模拟了车轮单次滚动,模型规模大,计算耗时,钢轨磨耗和轮轨型面不能迭代更新,导致磨耗水平较低,较低速度形成的磨耗特征波长不明显;轮轨瞬态冲击时轮轨线弹性材料即使超过其屈服极限,也不能模拟材料硬化和塑性累积过程,以致对磨耗结果可能有影响;1个转向架双轮对和2节车相邻转向架多轮对的振动波传递对钢轨模态约束作用也不可忽略。因此,未来的钢轨波磨仿真应该实现轮轨循环滚动接触,并引入合适的轮轨材料弹塑性本构关系和摩擦磨损模型,才能更加准确地模拟轮轨反复滚动后钢轨波磨萌生和发展过程。
5 结 论
(1) GJ-Ⅲ型扣件轨道出现的钢轨波磨波长为30~50 mm,为短波长波磨。车辆在不同线路上运行时速度变化范围为50~103 km·h−1,导致波磨通过频率为347~833 Hz。
(2) GJ-Ⅲ型扣件轨道在25~60 mm短波长凹陷激励下,轮轨垂向力显著频率为522~675 Hz,对波长40 mm的短波长凹陷激励响应最敏感;在车轮不同滚动速度激励下,轮轨垂向力显著频率为534~763 Hz,表现为频率固定机制;在白噪声激励下,钢轨垂向振动加速度显著频率为570~720 Hz。上述振动显著频率与钢轨波磨通过频率572~715 Hz接近。
(3) 车轮以 75,85,95和103 km·h−1滚动速度滚过短波长凹陷后形成的钢轨不平顺显著波长分别为31.5,31.5和40,40,40和50 mm,这与线路调查的钢轨波磨波长吻合。
(4) 直线段轮轨系统振动主要在垂向上占优,轮轨垂向力频率和车速是决定波磨波长的主要因素。GJ-Ⅲ型扣件轨道波磨的形成,并非钢轨1阶Pinned-Pinned共振引起,主要是轨道以670 Hz为中心的钢轨垂向弯曲高频固有特性被激发所致。

