380 km·h-1以上高速铁路插板式声屏障动力特性及响应分析

卫 星，戴李俊，温宗意，汪蓉蓉，胡 喆

（1.西南交通大学 土木工程学院，四川 成都 610031；2.中铁第四勘察设计院集团有限公司，湖北 武汉 430063）

声屏障在我国高铁线路上的应用十分广泛，且其结构形式多样。列车高速行驶通过时产生的脉动风压对声屏障结构的动力作用是声屏障结构设计需要关注的问题之一。

谢伟平等[1]进行了列车激励作用下地铁半封闭式声屏障的振动响应实测，发现声屏障立柱和亚克力板的振动加速度相对于桥面轨道板有显著的放大效应。列车低速运行时，声屏障结构响应存在一定的放大效应，那么当列车高速行驶时，声屏障结构所产生的动力响应更不容忽视。列车高速行驶产生的脉动风压作为对声屏障结构作用的主要影响因素，毕然等[2]通过数值模拟方法，建立车速为400 km·h−1时作用于直立式声屏障的脉动风压模型，与文献实测数据进行验证，并探究参数变化对脉动风压的影响规律。施洲等[3]在脉动风压力仿真与实测的基础上，给出车速为380～400 km·h−1时脉动风压的最大取值和广义振动频率范围等的建议。为探究列车高速行驶产生的脉动风压对不同形式声屏障的动力作用问题，卫星等[4]研究了不同开口形式的封闭式声屏障在列车以350 km·h−1速度通过时产生的脉动风压作用下的受力特性，研究表明越有利于风压释放的开口形式更有利于改善结构受力；吕坚品等[5]采用SAP2000软件建立了桥梁声屏障有限元模型，分析了脉动压力作用下声屏障的位移和弯矩峰值以及动力放大系数的分布特征；刘功玉等[6]分别进行了自然风、脉动风及二者叠加荷载作用下插板式声屏障的动力响应分析；康健等[7]分析了在列车脉动风压和重力双重作用下直立插板式声屏障H型钢立柱的受力与变形规律；焦长洲等[8]考虑桩-土-结构共同作用，进行脉动风压对设有桩基础的插板式声屏障结构振动响应影响的数值计算；在台风地区声屏障安全性问题的研究中，邓跞等[9]分析了整体式混凝土声屏障在不同工况下结构细部受力，并对加高1 m通透屏进行参数讨论。上述研究大部分以脉动风压作为主要的外部荷载，研究的结构形式多样，研究的角度也非常广泛，但针对铁路桥梁段和路基段常见的几种插板式声屏障结构，从380 km·h−1以上高速列车产生的脉动风压引起结构的振动响应特性这个角度的研究非常少。

为研究列车速度为380 km·h−1以上所产生的脉动风压引起的插板式声屏障结构振动响应特性，基于数值分析方法，进行不同车速和不同结构形式插板式声屏障的动力特性及响应研究，为高铁线路插板式声屏障的设计提供可靠的技术支持。

1 插板式声屏障结构形式及模型建立

高速铁路在桥梁段和路基段均设置有插板式声屏障，随着列车行驶速度提升，需要设计满足结构性能要求的插板式声屏障，本文研究的2类插板式声屏障的具体形式和高度见表1。

表1 插板式声屏障形式及高度

在桥梁段高2.3 m的PZ式和倒L型插板式声屏障以及路基段高3 m的直立型插板式声屏障的基础上，通过增设1 m高通透隔声板和变化立柱根部加劲板、加强钢板或桩基础尺寸，得到桥梁段高3.3 m的PZ式和倒L型插板式声屏障以及路基段高4 m的直立型插板式声屏障。桥梁段插板式声屏障布置图如图1所示，路基段插板式声屏障布置图如图2所示，6种不同结构形式的插板式声屏障立柱根部以及桩基础的细节如图3—图7所示。

图1 桥梁段声屏障示意图（单位：m）

图2 路基段声屏障示意图（单位：m）

图3 桥梁段高2.3 mPZ式声屏障立柱根部加劲板详图（单位：mm）

图4 桥梁段高3.3 mPZ式声屏障立柱根部加劲板详图（单位：mm）

图5 桥梁段倒L型声屏障立柱根部加强钢板详图（单位：mm）

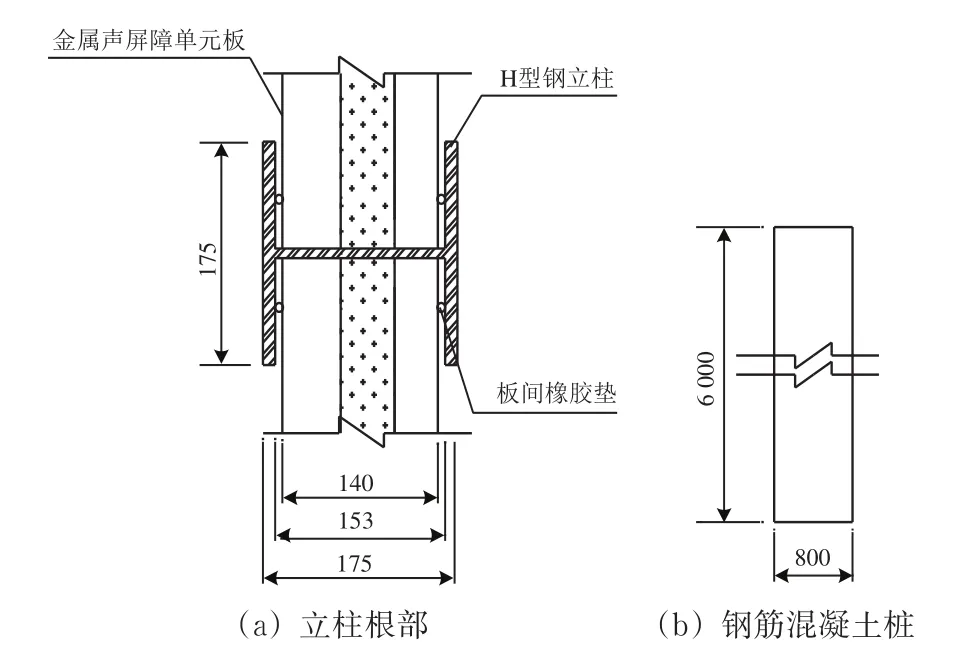
图6 路基段高3 m直立型声屏障立柱根部及桩基础详图（单位：mm）

图7 路基段高4 m直立型声屏障立柱根部加强钢板及桩基础详图（单位：mm）

2类插板式声屏障主要由金属声屏障单元板、通透隔声板、H型钢立柱、加劲板、加强钢板、钢支架、橡胶制品等部件组成。金属声屏障单元板以铝合金作为结构主材，铝合金面和背板厚度不小于1.5 mm；通透隔声板采用厚度不小于20 mm的加筋亚克力板，其上有防撞击防破损保护措施及防鸟撞击标志；H型钢立柱、加劲板、加强钢板、钢支架的材料采用Q235-B钢材；橡胶制品均采用三元乙丙橡胶；底梁和桩基础采用C30混凝土。

由赵丽滨[10]研究可知2根立柱之间结构形式相同时，声屏障结构的固有频率与基本结构单元的数量无关，为减少计算量，各结构形式均取10个节段，总长20 m；声屏障钢构件材料选用Q235钢，立柱采用梁单元模拟，立柱底部有加劲板或加强钢板时采用变截面梁单元模拟，倒L型声屏障的钢支架采用板单元模拟；金属声屏障单元板、通透隔声板材料根据实际设计参数进行材料拟定，采用板单元模拟。声屏障结构材料参数见表2[11]。

在连接关系上，桥梁段：立柱底部固结；立柱与吸声板之间采用弹性连接模拟纵桥向以及横桥向的橡胶连接效果；PZ式板与板之间采用释放板端弯矩模拟解耦器的连接效果；倒L型板与板之间通过弹性连接模拟橡胶条的连接效果，钢支架与立柱焊接部分采用刚性连接模拟。路基段：立柱底部和底梁以及桩基顶部依次刚性连接；立柱与吸声板，板与板通过弹性连接模拟橡胶条的连接效果；桩基空间计算模型通过设置弹性连接模拟，土弹簧刚度根据桩基M法计算，桩基主要控制参数见表3，不同深度截面的土弹簧刚度的具体计算参考文献[12]。

表2 声屏障结构材料参数

表3 桩基主要控制参数

不同形式插板式声屏障整体模型如图8所示。

图8 不同形式插板式声屏障整体模型图

2 声屏障结构固有动力特性

结构固有动力特性包含固有频率、阵型和阻尼。通过模态分析可以得到结构的固有频率和阵型，结构阻尼比一般在0.01～0.10之间，实际上阻尼对固有频率影响不大[13]。因此，模态分析的基本方程式为

式中：K为结构刚度矩阵；M为结构质量矩阵；λ为第i个特征值；ωi为第i阶角频率；φi为第i阶模态的特征向量。

通过模态分析得到的6个模型的自振基频的频率和模态特性见表4。图9给出了3个有代表性的模态。

表4 各模型自振基频

图9 自振基频模态图

由表4可以发现：不同结构形式插板式声屏障均在增设1 m高通透隔声板后自振基频频率减小；其基频模态均为整体侧向弯曲。

阻尼的计算选用瑞利阻尼，即

式中：C为瑞利阻尼矩阵；α为质量矩阵系数；β为刚度矩阵系数。

根据正交性原理，任意1阶模态阻尼比ξi和角频率ωi满足

依据钢结构抗震要求[14]，阻尼比取0.02。时程分析选用阵型叠加法，通过求得各模型的自振频率和阵型，选取参振质量达到总质量90%的频率作为频率范围的上限，结构自振基频作为频率范围的下限。根据所选频率范围的上下限，通过下式即可得到相应的质量和刚度矩阵系数，即

式中：ωa为频率下限；ωb为频率上限。

6种模型的质量和刚度矩阵系数见表5。

表5 各个声屏障结构的α和β

3 声屏障结构动力响应

结构动力分析相较于静力分析有很大的区别，前者还需考虑因质量运动产生的惯性力以及荷载和结构响应随时间变化的性质。实际中设计者更关心动力响应下的结果，通过动力放大系数将静力结果转化为动力结果。

3.1 脉动风压时程函数

脉动风压测点在各声屏障垂向由下至上布设，第1个测点高为0.2 m，其余测点高度按0.5 m依次增加，因此2.3，3.3，3，4 m 4种高度的声屏障模型分别布置5，7，6和8个测点，由此将靠近列车运行线路中心线一侧的声屏障板单元按垂向由下至上划分区间为N1—N5，N1—N7，N1—N6，N1—N8，并将各测点的脉动风压对应至划分的区间。

为研究不同车速和不同结构插板式声屏障的动力响应，选用380，400和420 km·h−1共3种车速，各工况列车行驶产生的脉动风压由西南交通大学李小珍教授课题组计算得到。图10给出了列车以车速400 km·h−1驶过路基段高3 m直立型声屏障时，提取的各测区脉动风压时程曲线。各测区风压峰值见表6。

图10 声屏障单元板表面脉动风压时程函数

表6 路基段高3 m直立型声屏障单元板表面脉动风压峰值

3.2 动力响应

有限元分析得到的各模型动力响应结果表明，不同结构形式的插板式声屏障结构在立柱的横向位移、纵向弯矩的峰值位置基本一致，最大横向位移出现在立柱顶部，最大纵向弯矩出现在立柱底部，部分结构形式模型的组合应力受加劲板或加强钢板影响，最大组合应力由底部移至加劲板或加强钢板处。图11给出了6种结构形式立柱横向位移时程。

图11 3种车速下6种声屏障横向位移时程

由图11可见：车速从380 km·h−1提高到400 km·h−1再提高到420 km·h−1的过程中，桥梁段PZ式和倒L型插板式声屏障高为2.3 m时，立柱最大横向位移正负峰值均随车速的增大而增大，增设1 m高通透隔声板后，立柱最大横向位移正负峰值先增大后减小；路基段直立型插板式声屏障高增设1 m高通透隔声板前后，立柱最大横向位移正负峰值均随车速的增大而增大。

表7给出了所有工况声屏障立柱动力响应最大值及相应放大系数。

表7 动力响应结果

从表7可见：在车速为380，400和420 km·h−1时，未设置1 m高通透隔声板的声屏障的动力响应均随车速增大而增大，此时最不利工况的车速为420 km·h−1；而设置1 m高通透隔声板后，当车速从400 km·h−1提升至420 km·h−1时，部分动力响应出现降低的情况，此时最不利工况的车速可能从420 km·h−1变化到400 km·h−1；车速从380 km·h−1提高到400 km·h−1再提高到420 km·h−1的过程中，桥梁段高2.3 m的PZ式、倒L型和路基段高3 m的直立型插板式声屏障立柱的横向位移、组合应力和纵向弯矩放大系数随车速增大而增大，增设1 m高通透隔声板后，立柱的横向位移、组合应力和纵向弯矩放大系数随车速增大先增大后减小；在相同车速下，增设1 m高通透隔声板后，立柱的横向位移、组合应力和纵向弯矩放大系数均增大。

增设1 m高通透隔声板后，车速为420 km·h−1相较于400 km·h−1时声屏障立柱的动力放大系数减小，原因为结构动力响应减小或增加幅度较小，而静力结果随着车速增加在增大，因此动力放大系数减小。

4 结论

（1）不同结构形式插板式声屏障均在增设1 m高通透隔声板后自振基频减小，且6个模型基频模态均为整体侧向弯曲。

（2） 在车速为380，400和420 km·h−1条件下，插板式声屏障立柱的横向位移、组合应力和纵向弯矩放大系数在未设置1 m高通透隔声板时均随车速的增大而增大，在增设1 m高通透隔声板时随车速的增大先增大后减小；在相同车速下，增设1 m高通透隔声板后，立柱的横向位移、组合应力和纵向弯矩放大系数均增大。

（3）针对380至420 km·h−1车速段的高铁线路上插板式声屏障的设计，对于未设置1 m高通透隔声板的结构形式，需要重点关注420 km·h−1车速下插板式声屏障结构的动力响应；对于增设1 m高通透隔声板的结构形式，重点关注420 km·h−1车速的同时，还需额外关注400 km·h−1车速下插板式声屏障结构的动力响应。