基于MMC的储能型同相供电系统模型及控制策略

陈民武，陈天舒，代先锋，廖红波

（西南交通大学 电气工程学院，四川 成都 611756）

目前，采用单相工频交流制式的牵引供电系统中存在着以负序功率为主的电能质量问题和电分相问题[1−2]。西南交通大学李群湛教授提出的同相供电技术方案[3−4]有效解决了以上问题，受到国内外学者的广泛关注并进行了深入研究[5−7]。2015年1月，首套单三相组合式同相供电系统在中南通道沙峪牵引变电所投入运行，整体运行性能良好。此外，采用同相供电技术的温州市域铁路S1线于2019年9月正式开通，广州地铁18号线于2021年9月正式开通。

同相补偿装置作为组合式同相供电系统的核心装置，一般采用级联H桥链式结构，通过多绕组隔离匹配变压器接入牵引母线。该结构满足了高压大容量的工程需求，并具有功率等级高、谐波含量低及模块化程度高等优点，但配套隔离匹配变压器后增加了资金投入、功率损耗和占地面积[8]。文献[9]将双星型多电平变换器应用于组合式同相供电系统中，以替代隔离匹配变压器，然而产生了均压环流问题。为避免以上问题，采用模块化多电平变流器（Modular Multilevel Converter，MMC）作为同相补偿装置，在无须配备隔离匹配变压器的同时保留了级联H桥链式结构的优点，并具有较低的开关频率与系统损耗[8]。

将储能系统（Energy Storage System，ESS）引入组合式同相供电系统，实现制动能量回收和负荷削峰填谷是目前的研究热点。在基于MMC的同相供电系统中引入ESS是一个全新的问题，需要考虑储能元件的特点、接入拓扑的优劣以及牵引负荷的特性。ESS中常用的储能元件有蓄电池、飞轮和超级电容（Super Capacitor，SC），其中SC较其他储能元件具有功率密度大、充放电速度快的特点[10]，能有效应对波动负荷的高频次储能需求。文献[11]将储能装置经过变流器接入牵引母线中，案例分析表明10 MW储能容量下每年可节省电费616万元。将储能装置接入同相补偿装置的公共直流母线可简化储能装置并网结构，但其中大量串并联结构将导致储能系统可靠性降低[12]。储能单元分散接入MMC的子模块（Sub-Module，SM）中可简化接入结构并提升可靠性，但其储能容量利用率仍然受到单个储能单元荷电状态（State of Charge，SOC）的限制[13]。目前基于MMC的储能系统采用的SOC均衡控制策略一般是通过载波移相调制策略对单个储能单元进行功率控制[14]，系统响应速度快但提高了控制策略的复杂度。采用零序电压注入法实现相间SOC均衡，存在计算繁琐效率偏低的问题[15]；采用反步法分配储能功率实现桥臂内的SOC均衡，子模块电压波动大、电容需求高[16]。

本文建立了基于MMC的储能型同相供电系统模型，基于负荷特性划分了再生制动、削峰、填谷3种工作模式，并在各工作模式下以国标限值为约束整定了功率目标，提出了一种分层协调控制策略，其中新的SOC均衡控制基于排序算法实现不受MMC调制策略限制，在此基础上建立了储能型同相供电系统仿真模型，并对牵引负荷的不同工况进行仿真验证。

1 基于MMC的储能型组合式同相供电系统模型

1.1 主电路工作原理

单三相组合式同相供电系统由单相牵引变压器（Traction Transformer，TT）、高压匹配变压器（High voltage Matching Transformer，HMT）及同相补偿装置构成，其中HMT使用接线方式为YNd11的降压变压器，并采用平衡接线与TT进行连接，形成90°电压相位差。系统主电路拓扑如图1所示。图中：Uj和Ij分别为三相电网电压和电流，相数j=A，B，C；IT1和Ij1分别为TT和HMT的一次侧电流；IT为TT的二次侧电流；Ux和Ix为补偿装置α端口和β端口的电压和电流，端口x=α，β；Udc为直流母线电压；UC为子模块电压；L为桥臂电感；Lα和Lβ为扼流电感。

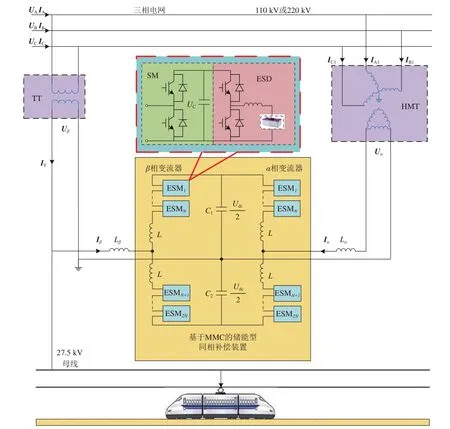
图1 单三相组合式同相供电系统主电路拓扑

由图1可知：同相补偿装置的α端口通过HMT消除TT产生的负序功率；β端口与TT相连共同为牵引机车供电，以取消电分相，实现同相供电功能；同相补偿装置采用两桥臂MMC拓扑，相比于其他拓扑其结构最为简单，同时其单相控制方式易于实现；两桥臂拓扑中由a与b这2个桥臂构成交直交变流器连接α端口和β端口，其直流母线上并联有稳压电容C1和C2提供中性点；每相上、下桥臂皆由N个子模块与桥臂电感L串联构成，并通过扼流电感Lα和Lβ与α和β端口相连接；子模块可通过半桥型DC-DC变换器连接超级电容，以构成储能子模块（Energy Sub-Module，ESM），其由子模块（SM）与储能装置（Energy Storage De⁃vice，ESD）构成。

1.2 储能型同相补偿装置工作原理

图1中储能装置采用半桥型拓扑将超级电容接入MMC，其充放电原理较为简单不做赘述，因此仅对MMC工作原理进行分析。由图1中交直交变流器电路拓扑得MMC单相等效电路如图2所示，其中串联的储能子模块等效为可控电压源，桥臂电感等效为受控电压源，直流母线等效为2个串联直流电压源并提供中性点O。图中：uy为上下桥臂子模块等效电压瞬时值，桥臂y=p，n；uZ为桥臂电感等效电压瞬时值；iy为上下桥臂中流过的电流；uS和iS分别为交流侧电压电流；iZ为桥臂间环流；L'为网侧等效电感。

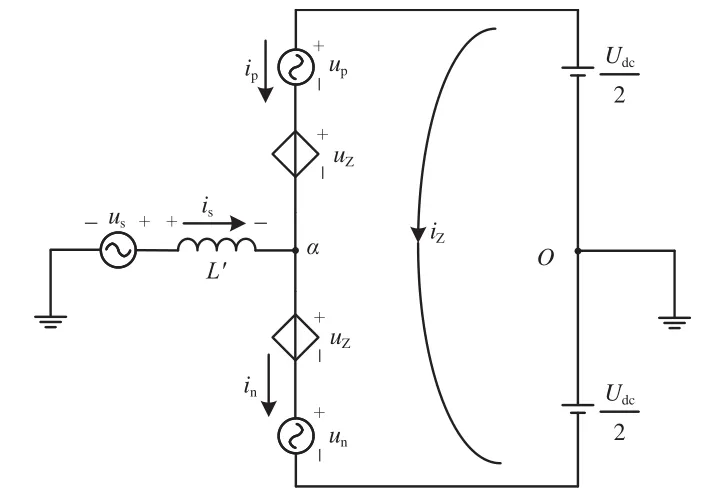
图2 MMC单相等效电路

MMC稳定运行的前提是保持直流母线电压稳定，即每个桥臂每个时刻投入的子模块数量恒定为N且每个子模块电压稳定。忽略桥臂电感上电压，可知

根据基尔霍夫电流定律可得

分析上下桥臂回路可得

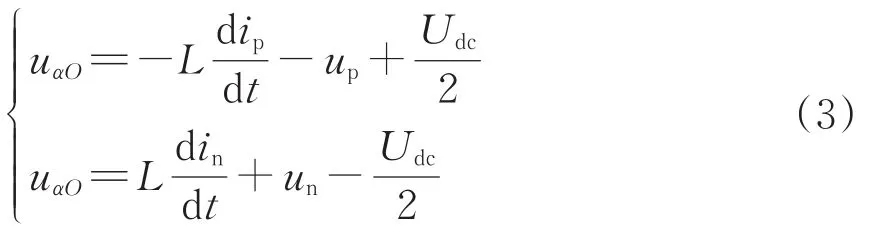
整理式（3）并代入式（2），并将桥臂电感L等效为输出端口上电感L'可得

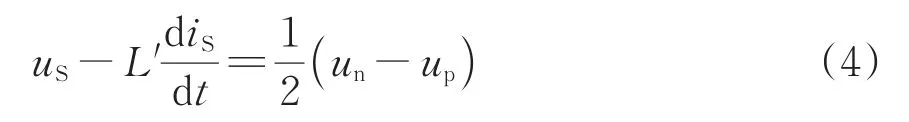
在式（1）的限制下调节上下桥臂可控电压源的差值，即可控制端口的输出电压和电流。

2 工作模式

根据牵引负荷的状态和大小，将工作模式划分为再生制动模式、削峰模式和填谷模式3种，划分条件见表1。表中：Pl为牵引负荷功率；PESM为储能装置最大充放电功率；PL为填谷模式切换阈值功率；PH为削峰模式切换阈值功率；PESM，PL和PH均为正值。

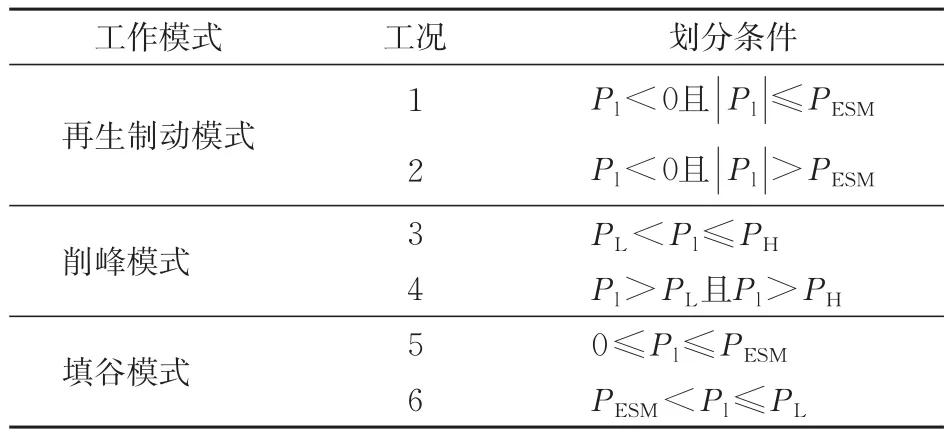
表1 工作模式划分

2.1 再生制动模式

当列车进行再生制动时，系统将进入再生制动模式。在此模式中牵引负荷功率Pl小于零，也称为再生制动功率，并根据再生制动功率是否大于储能装置最大充放电功率可分为2种工况。再生制动模式下各端口功率关系如图3所示。图中：PTT为TT端口功率；Pα和Pβ为同相补偿装置α端口和β端口功率；PES为储能装置端口功率。

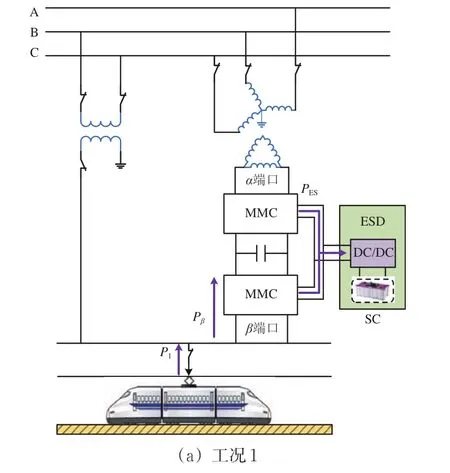
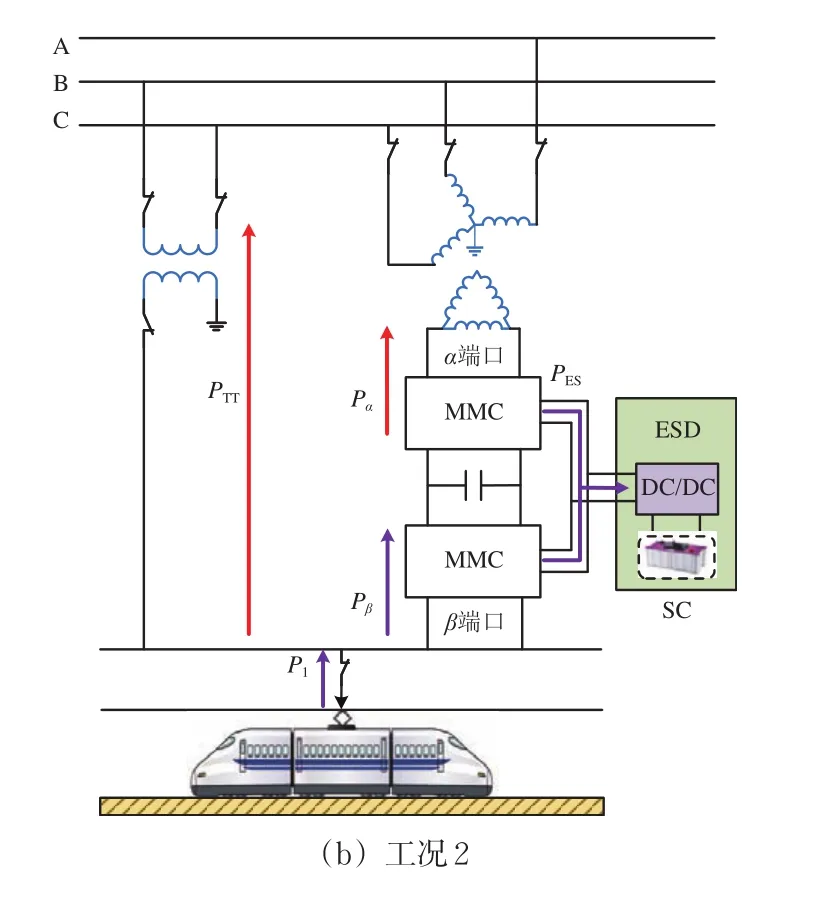
图3 再生制动模式下各端口功率关系

1）工况1

该工况下，再生制动能量全部通过同相补偿装置的β端口由储能装置吸收，同相补偿装置端口功率与储能装置端口功率间的关系为

2）工况2

该工况下，再生制动能量部分通过同相补偿装置的β端口由储能装置吸收，需要补偿的再生制动能量通过同相补偿装置和TT返送回电网，MMC与储能装置端口功率的关系为

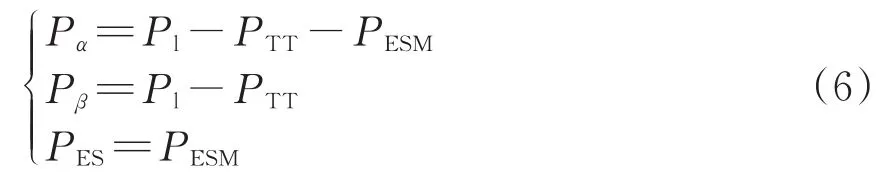
在国标三相不平衡度约束下对端口功率进行配置，通过TT和同相补偿装置的功率为

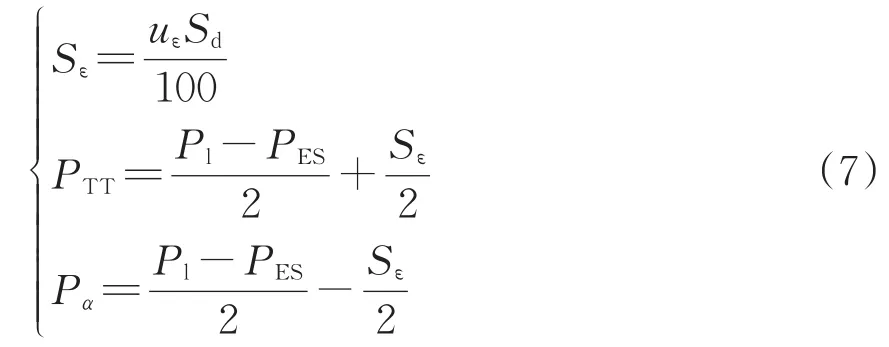
式中：Sε为负序功率上限；uε为国标三相不平衡度；Sd为三相电网短路容量。

将式（6）带入式（7）可得

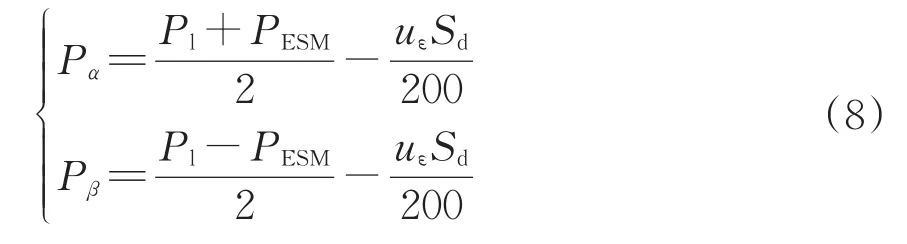
2.2 削峰模式

组合式同相供电系统为有功平衡方式，同相补偿装置与TT各分担一半牵引负荷以实现负序补偿。超级电容储能系统工作也能分担牵引负荷，进一步降低对电网的冲击。该模式中Pl大于填谷阈值PL，并根据Pl是否大于削峰阈值PH分为2种工况。削峰模式下各端口功率关系如图4所示。

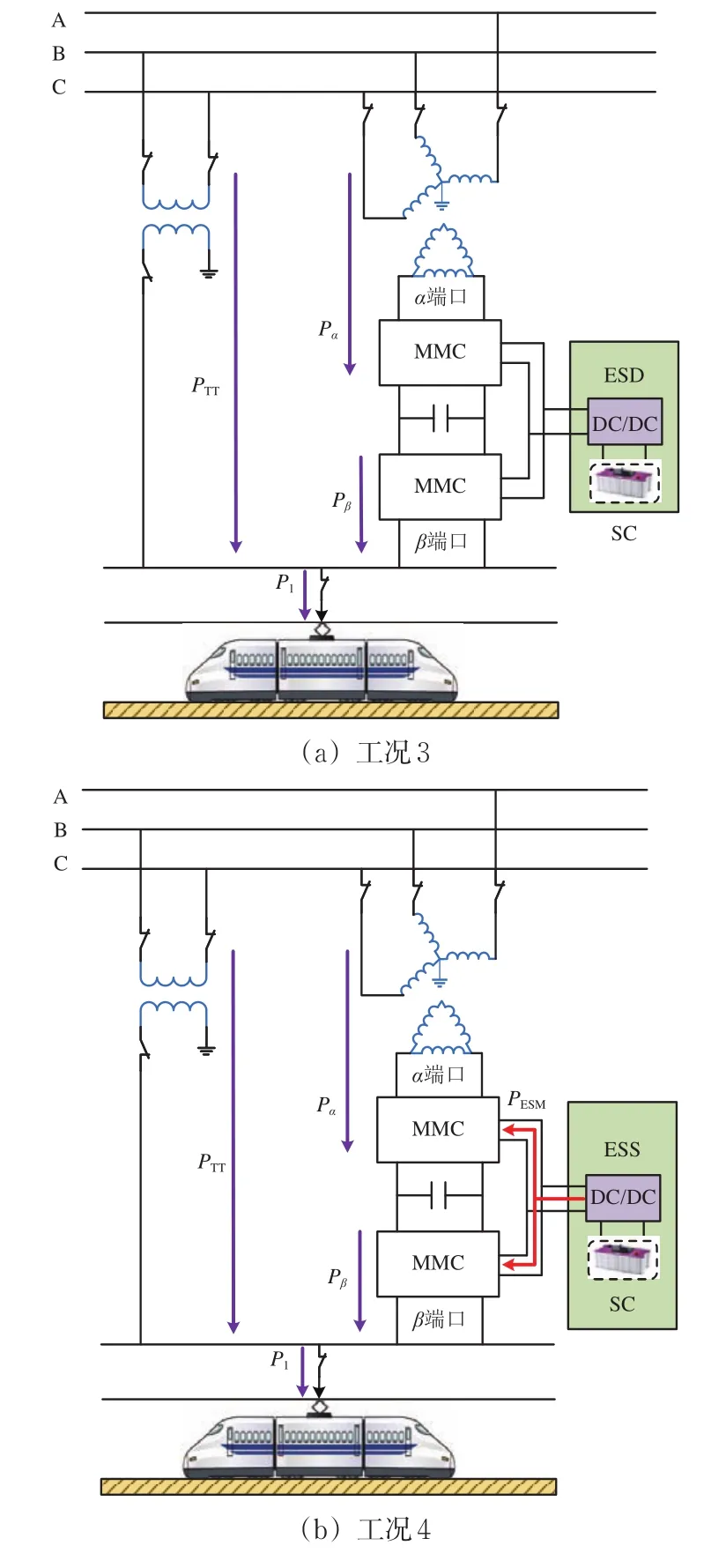
图4 削峰模式下各端口功率关系

1）工况3

此时，储能装置处于等待状态不工作，由TT承担主要牵引负荷功率，而同相补偿装置承担剩余功率，MMC与储能装置端口功率的关系为

在国标三相不平衡度限值约束下对端口功率进行配置，通过TT和同相补偿装置的功率为

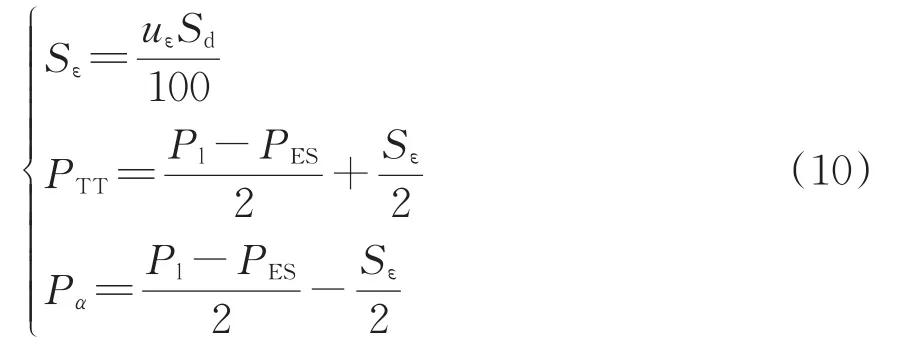
将式（9）代入式（10）可得

2）工况4

此时，储能系统与同相补偿装置共同分担一部分牵引负荷，剩余牵引功率由TT提供，MMC与储能装置端口功率的关系为

在国标三相不平衡度约束下对端口功率进行配置，通过TT和同相补偿装置的功率为

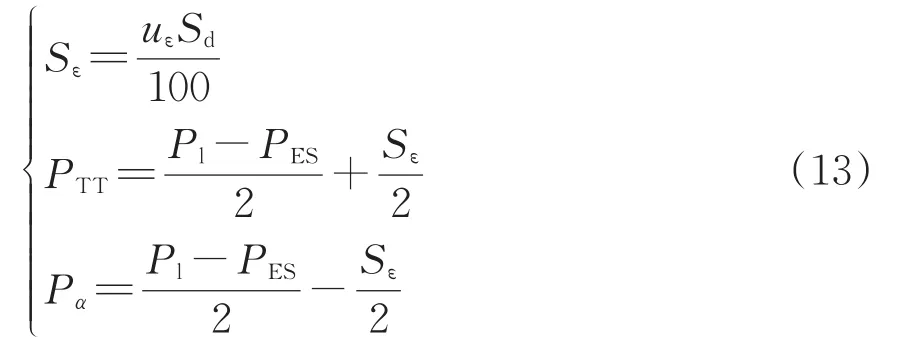
将式（12）代入式（13）可得

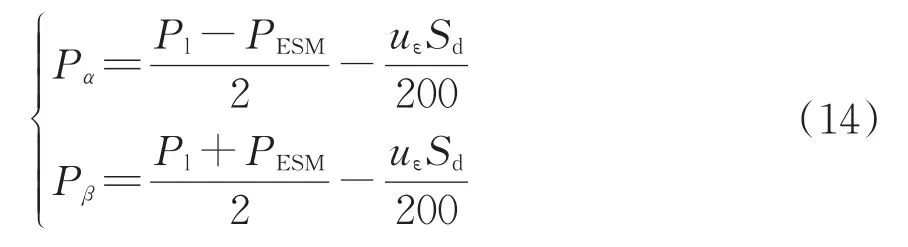
2.3 填谷模式

为确保储能系统的正常运行，其充电能量不仅来自再生制动过程还可在负荷较轻时从电网获取。该模式中Pl小于填谷阈值PL并根据Pl是否大于PESM分为2种工况。填谷模式下各端口功率关系如图5所示。

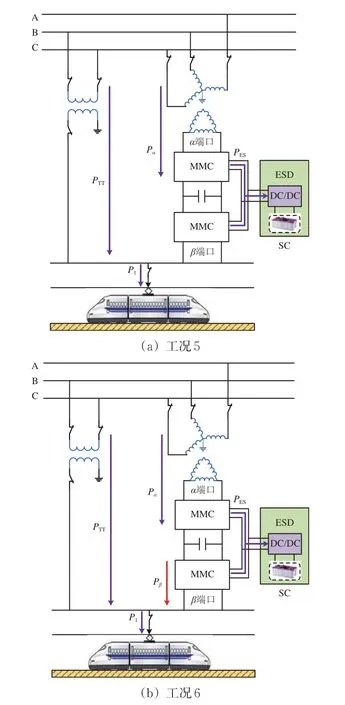
图5 填谷模式下各端口功率关系

1）工况5

仅由储能装置工作即可平衡牵引负荷对电网的负序功率，MMC变流器与储能装置端口功率的关系为

2）工况6

为实现完全补偿，将储能装置最大充电功率与牵引负荷相加得到实际消耗功率，MMC变流器和储能装置端口功率为

3 分层协调控制策略

同相补偿装置与储能装置作为同相供电系统的主要设备，需要一种控制策略来实现其有效配合。以第2节的工作模式为基础，提出了包括上层功率配置和下层端口电流控制的分层协调控制策略，使同相补偿装置具有良好的动态响应和波形质量。

3.1 上层功率配置

系统的功率配置过程如图6所示。首先，检测负载功率值并根据阈值判断工作模式。然后，根据第2节中功率关系计算各端口参考功率，传递到下层端口电流控制部分。

图6 上层功率配置

3.2 下层端口电流控制

由上文功率配置得到MMC与储能装置端口功率，通过MMC控制策略实现α端口和β端口的电流控制，通过SOC均衡控制对各储能装置功率进行重新分配，并采用双环控制实现储能装置的充放电。下层端口电流控制如图7所示。图中：变量的上标“*”表示其为参考值，例如P*α/P*β为α端口或β端口功率的参考值；Pxyk为x相y桥臂第k个储能装置的参考功率，k=1，2，…，N；UES和IES分别为超级电容的输出电压和电流；UCave为该相所有子模块电压的均值；G为开关控制信号。

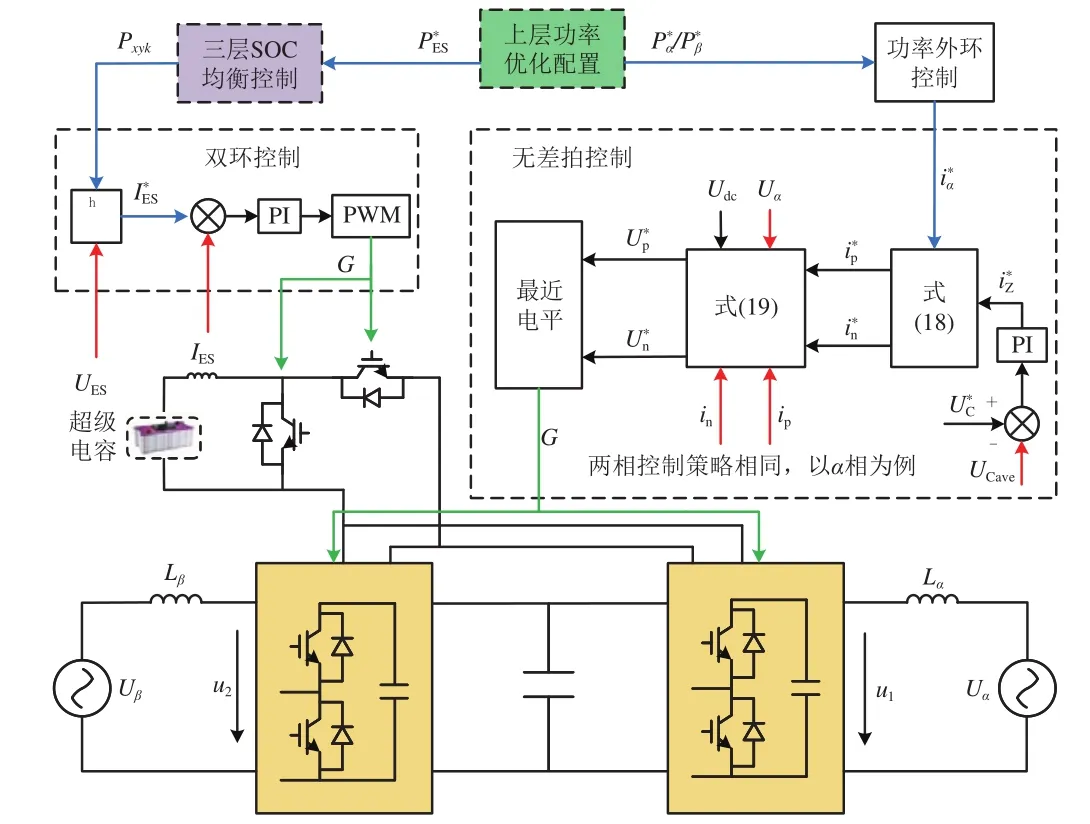
图7 下层端口电流控制

3.2.1 MMC控制

采用无差拍电流控制策略，该策略依靠系统数学模型获得控制结构与控制参数[17]，因此需要通过图2所示MMC单相等效电路推导其无差拍控制算法，如图7所示。具体推导过程如下。

在等效电路中引入环流变量iZ，为

将其代入式（2）可得

MMC环流能够给子模块电容充电以保持电压稳定和抵消损耗，将子模块电压参考值UC*与上下桥臂子模块电压均值UCave差值通过PI控制作为环流参考值，可以做到无静差控制以减小纹波与2倍频谐波。

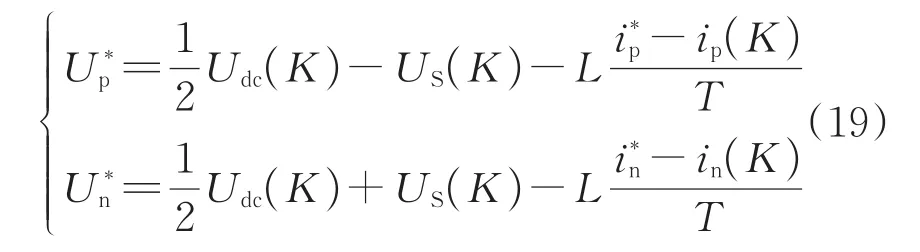
3.2.2 储能装置功率控制

基于功率控制的储能装置，提出了一种3层SOC均衡控制策略包括采用排序算法实现桥臂内SOC均衡，对相间和上下桥臂间SOC均值进行闭环反馈控制，生成差值功率修正系数实现相间与桥臂均衡。

定义x相y桥臂第k个储能装置的SOC值为Sxyk，桥臂中所有储能单元SOC均值为单相中所有储能单元SOC均值等于该相上下桥臂储能单元SOC均值的平均值。各均值间关系为

3层SOC均衡控制框图如图8所示。

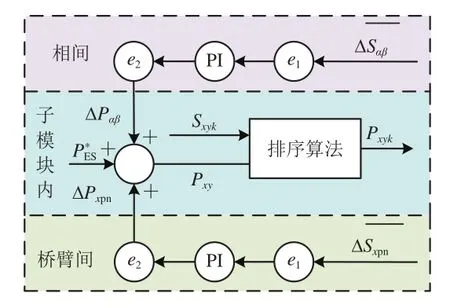
图8 3层SOC均衡控制框图

4 算例分析

为了验证上文建立的系统模型和控制策略的正确性和有效性，基于MATLAB/Simulink仿真平台搭建基于MMC的储能型同相供电系统仿真模型，具体仿真参数见表2。

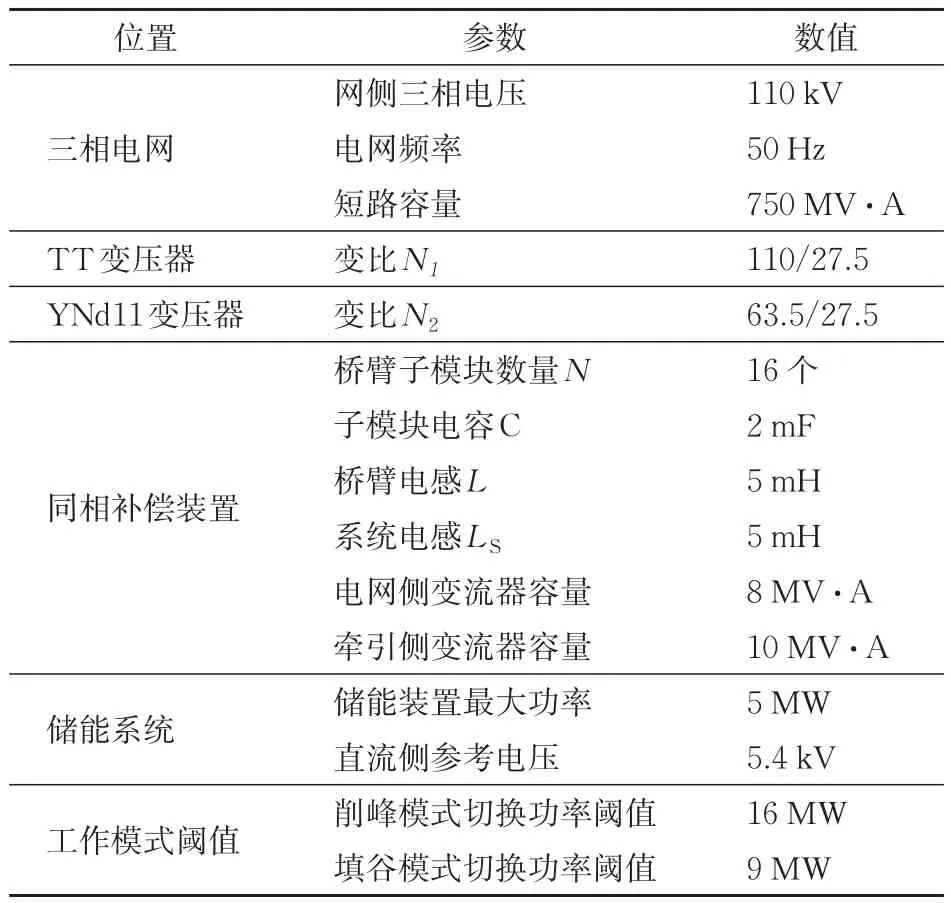
表2 系统仿真参数

4.1 再生制动模式下仿真结果

再生制动模式下仿真波形如图9所示。图中：图（b），（c）和（d）的工况与图（a）工况相同；ε为三相电压不平衡度；UCP−P为1个周期内子模块电压峰-峰值；α7表示α相模块7，上1表示上桥臂模块1，其余同理。

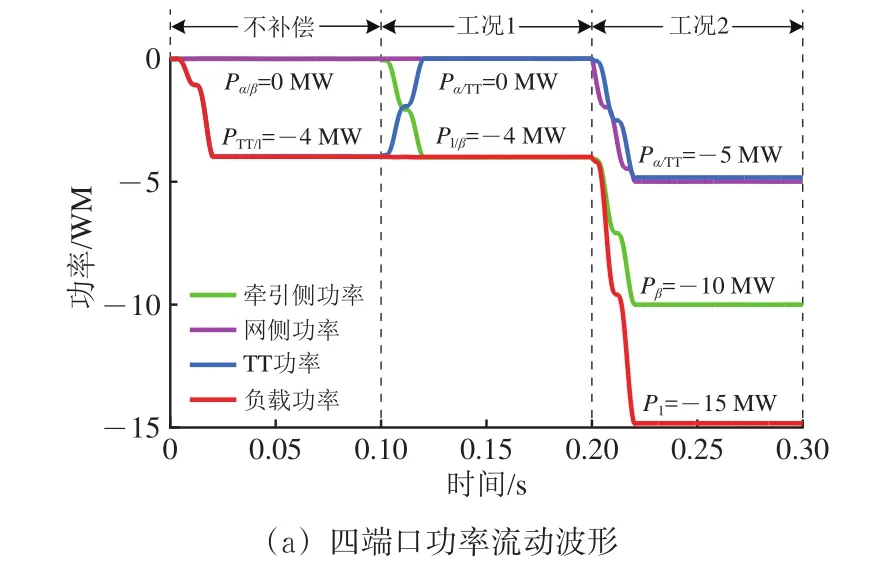
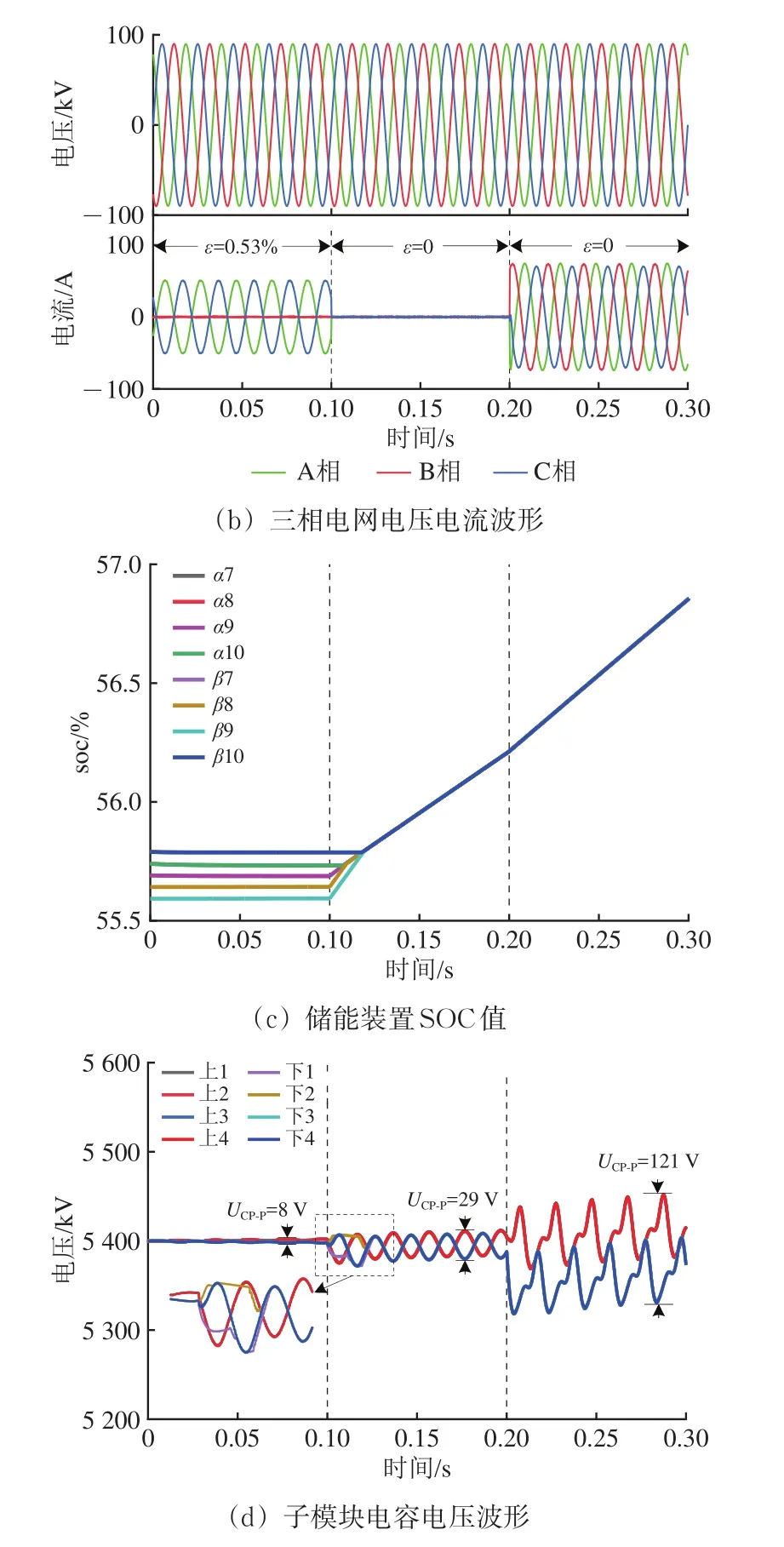
图9 再生制动模式下仿真波形

由图9（a）可知：0～0.1 s时再生制动功率为4 MW，储能装置不工作，能量完全反馈回电网；0.1～0.2 s时再生制动功率为4 MW，系统处于工况1，储能装置回收全部再生制动能量；0.2～0.3 s时再生制动功率增加至15 MW，系统处于工况2，储能装置以最大功率工作，剩余再生制动能量反馈回电网。

由图9（b）可知：补偿前后ε由0.53%降至0，同相补偿装置实现了完全补偿目标。

由图9（c）可知：0.1 s时储能系统开始充电，经过0.02 s后各SOC值均衡一致；0.1～0.2 s再生制动能量利用率为100%，0.2～0.3 s再生制动能量利用率为(Pβ−Pα)/Pl=33.3%。

由图9（d）可知：子模块电压均保持稳定，最大波动为121 V即2.2%，0.1 s时反应储能装置工作略有失稳后迅速稳定。

以上结果证明了系统在再生制动工作模式下的有效性。

4.2 削峰模式下仿真结果

削峰模式下仿真波形如图10所示。图中：图（b），（c），（d）的工况与图（a）工况相同。

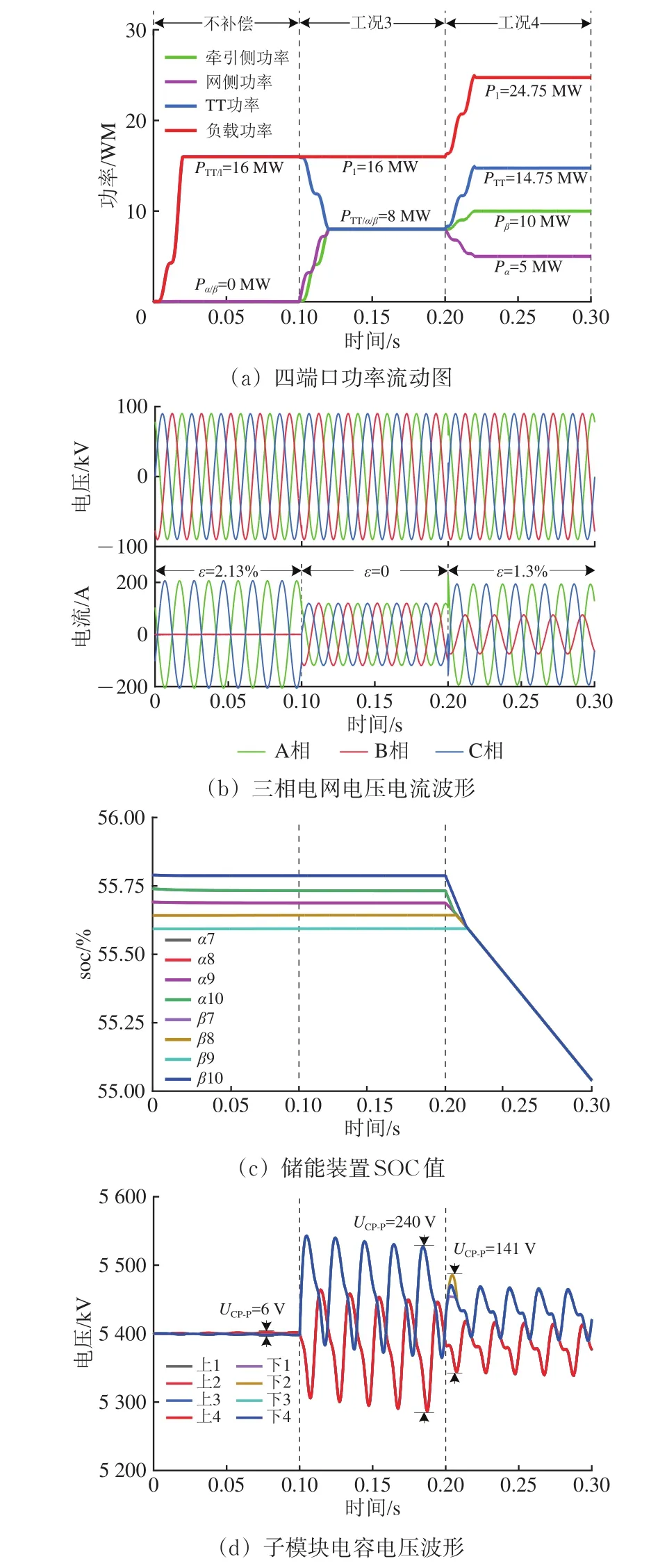
图10 削峰模式下仿真波形

由图10（a）可知：0～0.1 s时牵引负荷为16 MW，完全由牵引变压器承担；0.1～0.2 s时牵引负荷为16 MW，系统进行完全补偿，处于工况3；0.2～0.3 s时牵引负荷为24.75 MW，储能开始工作以降低峰值负荷，系统处于工况4，系统容量不足以完全补偿，以不平衡度1.3%[18]为约束进行部分补偿。

由图10（b）可知：补偿前后ε由2.13%降至0再升至1.3%，同相补偿装置实现了完全补偿和部分补偿目标。

由图10（c）可知：0.2 s时储能装置放电，经过0.02 s后各SOC值均衡一致。

由图10（d）可知：子模块电压均保持稳定，最大波动为240 V即4.4%。

以上结果证明了系统在削峰工作模式下的有效性。

4.3 填谷模式下仿真结果

填谷模式下不设置不补偿对照工况，各工况下均以完全补偿作为目标。填谷模式下仿真波形如图11所示。图中：图（b），（c），（d）的工况与图（a）工况相同。

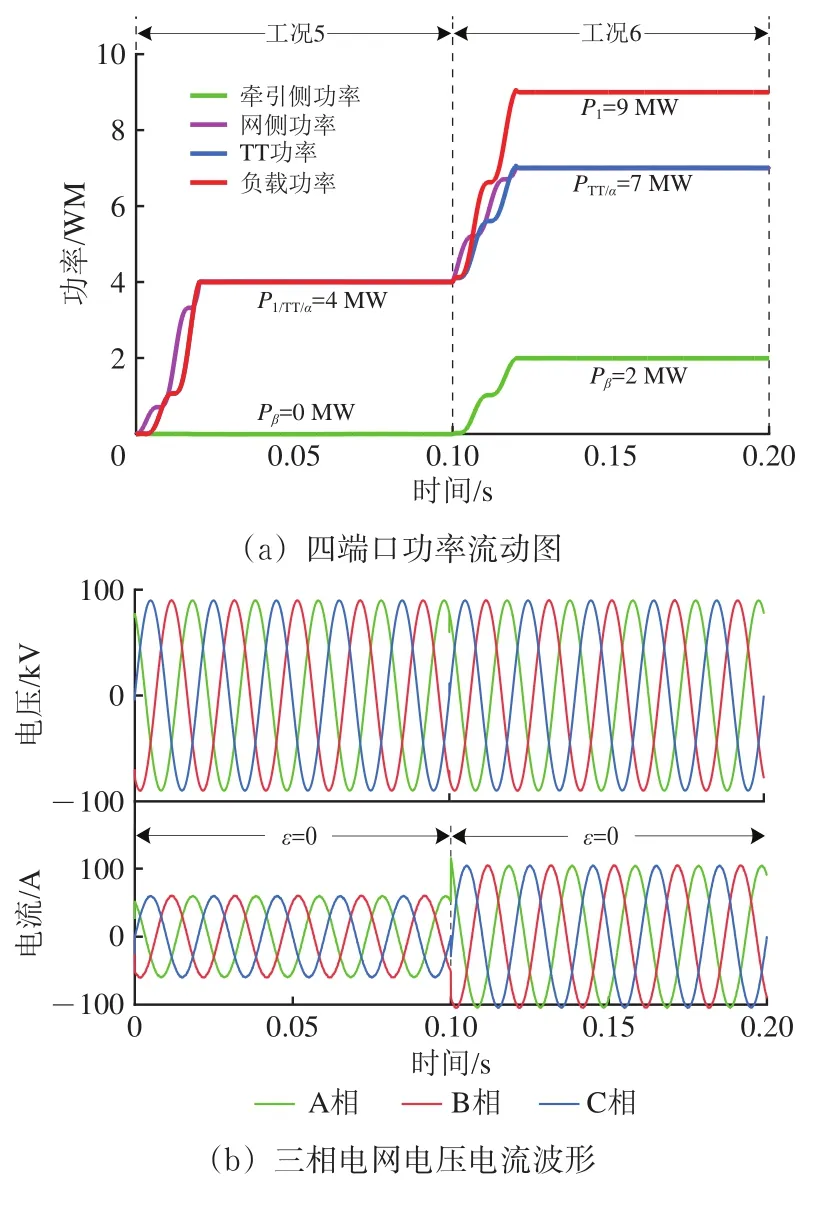
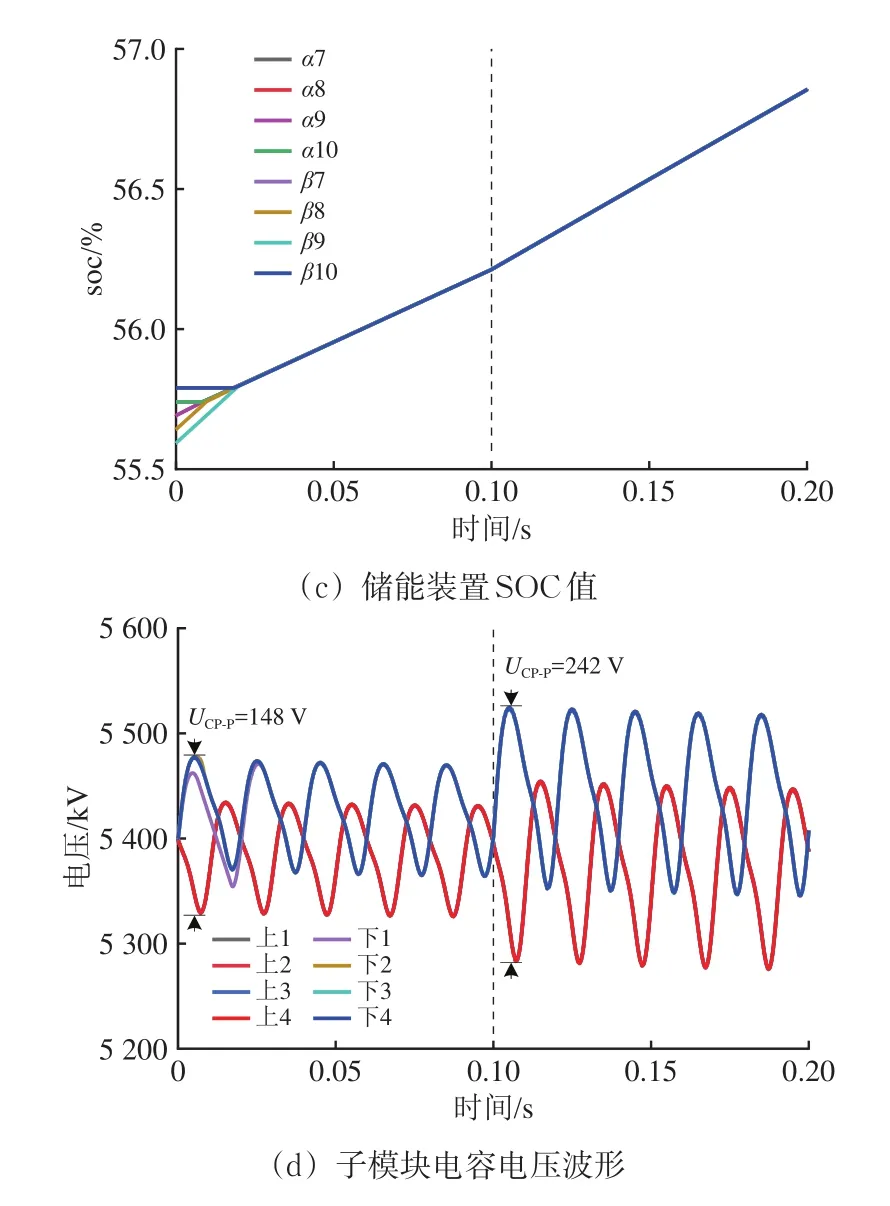
图11 填谷模式下仿真波形

由图11可知：0～0.1 s时牵引负荷功率为4 MW，系统处于工况5，0.1～0.2 s时牵引负荷增大到9 MW，系统处于工况6；2个工况下ε均保持为0，同相补偿装置实现了完全补偿目标；0 s时储能系统开始充电，经过0.02 s后各SOC值均衡一致；子模块电压均保持稳定，最大波动为242 V即4.5%。

以上结果证明了系统在填谷工作模式下的有效性。

4.4 分层协调控制仿真结果

协调控制下仿真波形如图12所示。图中：图（b），（c），（d）的工况与图（a）工况相同。

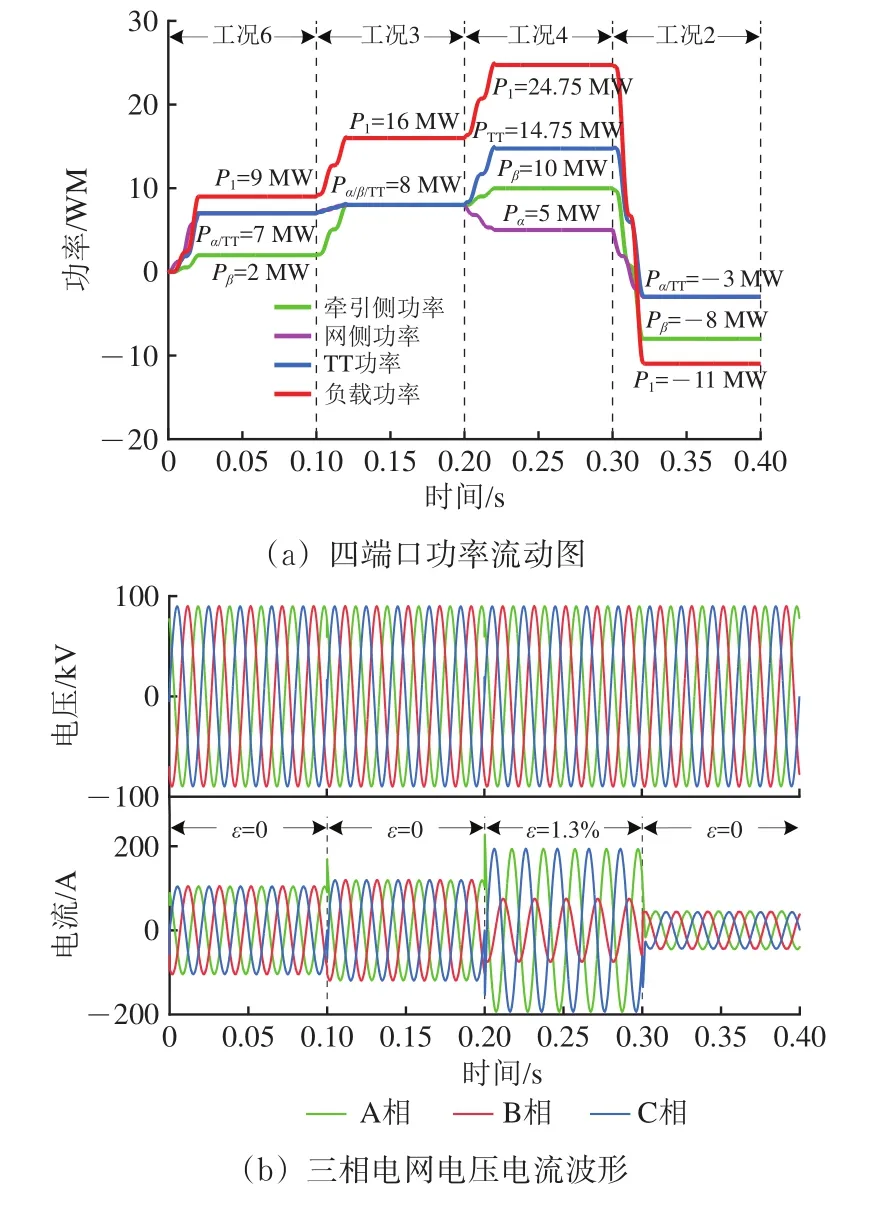
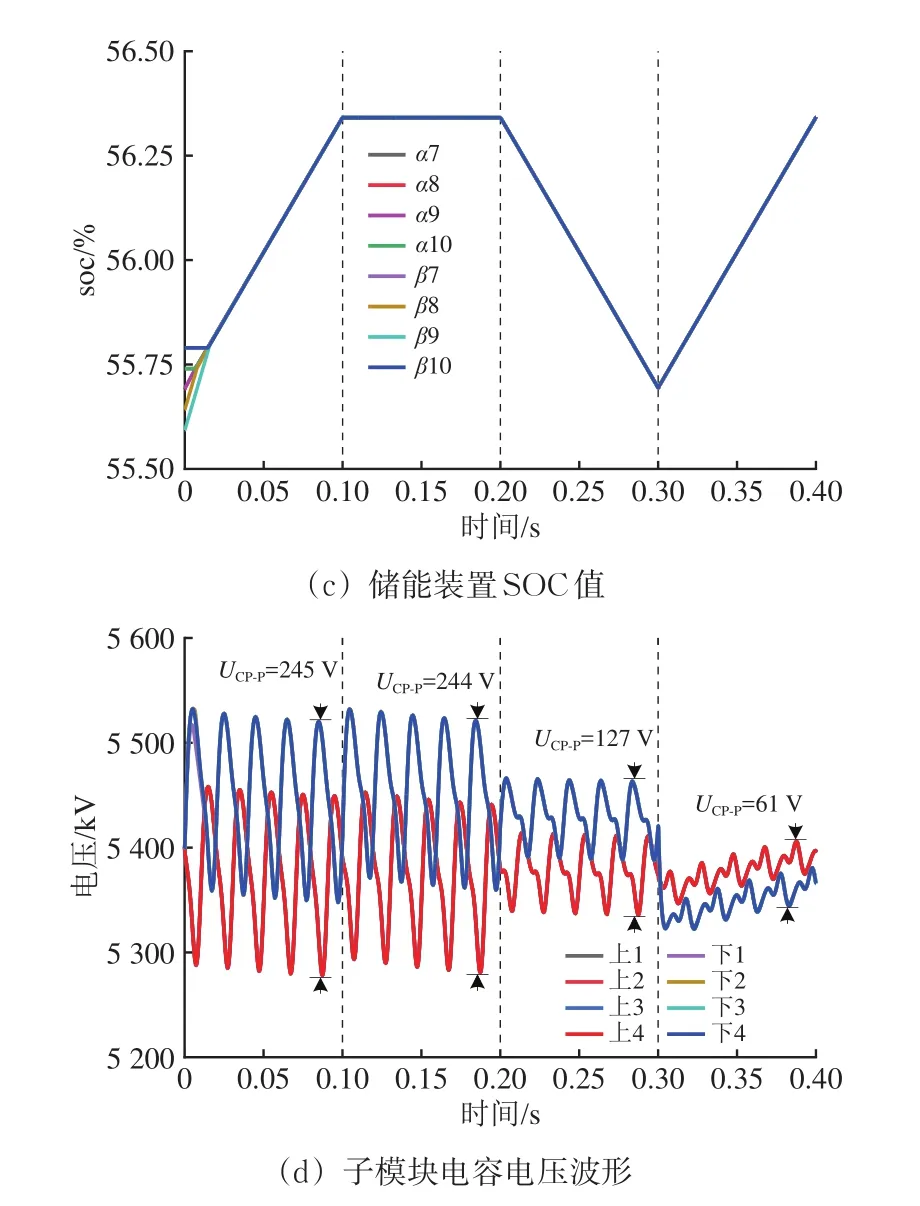
图12 协调控制下仿真波形

由图12可知：0～0.1 s时牵引负荷功率为9 MW（工况6），0.1～0.2 s时牵引负荷为16 MW（工况3），0.2～0.3 s时牵引负荷为24.75 MW（工况4），0.3～0.4 s时机车处于再生制动状态，再生制动功率11 MW（工况2）；ε在0.2～0.3 s时为1.3%，其余时间为0，同相补偿装置实现了完全补偿及部分补偿目标，且能够在工况间快速切换；储能装置经过充电、保持和放电循环后SOC值不变，说明功率控制有效，同时SOC均衡后保持一致，0.3～0.4 s制动能量利用率为(Pβ−Pα)/Pl=45.5%；子模块电压均保持稳定，0.3 s时变流器功率流向逆转同时子模块电压跳变、上下桥臂电压对称关系反转，子模块电压最大波动为245 V即4.5%。

仿真结果反映了工作模式间的有效切换，验证了分层协调控制策略的有效性。

5 结 论

（1）同相补偿装置采用两桥臂MMC变流器拓扑结合储能装置，实现了牵引负荷、储能系统和电网的有功流动，无须隔离变压器，降低了损耗与占地。

（2）基于同相拓扑结合牵引负荷特性划分了3种工作模式，以相关国标值为约束计算了各端口参考电流。仿真验证了在负荷较小与再生制动工况下可以实现完全补偿，在负荷较大时可以满足国标限值的负序补偿要求。

（3）提出一种分层协调控制策略，其下层控制中基于排序算法的3层SOC均衡策略与无差拍控制策略协调控制储能装置和MMC，仿真验证了SOC均衡时间为0.02 s，保证了储能系统的稳定运行。

（4）建立了系统的仿真模型，并对3种不同工作模式及其切换进行了仿真分析，验证了系统具有良好的动态响应和运行稳定性，可以实现再生制动能量的高效利用。