基于大数据的矿山边坡稳定性评价模型

于 雷,闫 岩,邓巧巧

（1．核工业二四三大队，内蒙古 赤峰 024000；2．内蒙古赤峰地质矿产勘查开发院，内蒙古 赤峰 024000）

1 引言

边坡岩土体在一定坡高、坡角等条件下的稳定程度就叫作边坡稳定性，与铁路、市政、公路、矿山、土建等工程领域息息相关[1]。其中因边坡失稳引发的山体滑坡就是一种不局限于区域与破坏性的巨大地质灾害，形成时不易被察觉，发生时极易造成片状的连带效果，故研究边坡稳定性具有重要的现实意义，通过分析、自动评价边坡稳定性，可以有效防止边坡失稳带来的危害。

国内外学者对此进行大量研究，文献[2]基于某露天煤矿的边坡进行稳定性研究，通过边坡地质调查、工程地质钻探等，对南端帮边坡工程地质与水文地质条件展开分析；文献[3]根据边坡冻融作用对边坡的影响与稳定性情况，规划出边坡结构参数优化方法与局部失稳加固治理策略。

基于上述文献方法优势，本文以大数据为基础，深入研究矿山边坡稳定性评价模型。引入松弛变量，避免模型出现过拟合现象；通过数据预处理，提升边坡失稳判断准确度，反映边坡结构稳定性的实际情况，发出正确的预警信号。

2 基于大数据环境的边坡稳定性自动评价模型构建

在矿山工程地质的基础上，根据地层岩性、坡度、岩体变形破坏分类等因素，将矿区坡度划分为几个分区，反映了不同区域的坡度特征，作为边坡稳定性的对象。为建设边坡稳定性自动评价模型，对采集到的大数据进行预处理，包括数据聚类、异常数据识别、数据修正以及平滑处理，实现自动评价模型构建。

2.1 大数据预处理

用传感器采集到的大数据较为复杂，有一定几率存在偶然性误差，对边坡稳定性产生错误的自动评价结果，所以，需要在使用数据前进行一系列数据清理操作。

2.1.1 数据聚类

边坡失稳前后存在一定数据特点，通过去除初始数据的异常数据，取得数据基本特征，提升边坡失稳判断准确度[5]。

假设隶属矩阵U的取值范围是[0，1]，则经归一化的各数据隶属度和是1，表达式如下所示：

公式(1)中，c表示子类数量。

采用下列公式表达目标函数：

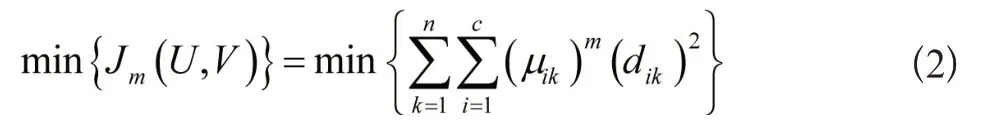
公式(2)中，第k个数据点与第i类的相似度用μik表示，取值范围是μik[0，1]，数据点与类别间的欧几里得距离用dik表示，加权指数为m，取值范围是m[0，2]。

依据聚类准则架构下列拉格朗日函数：

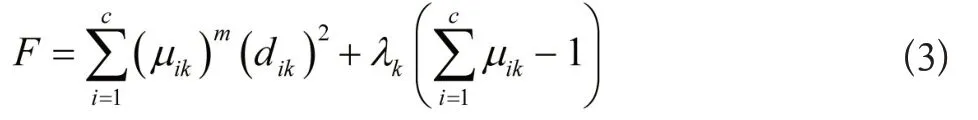
为提升线性可分概率，简化计算过程，将核诱导距离的两项相加后替换欧几里得距离，得到下列聚类目标表达式：

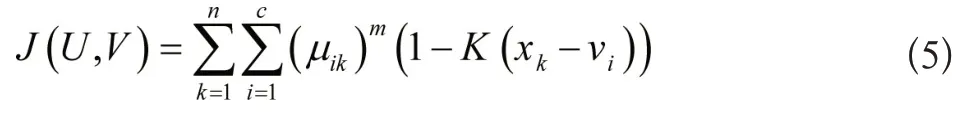
公式(5)中，vi表示模糊类划分的第e个聚类中心，计算的个体数量为xk，k(xk-vi)表示高斯核函数。

在核函数中引入动态权重αi，赋予数据点多的类别更多权重，增加数据元素隶属度，构建下列目标函数表达式：

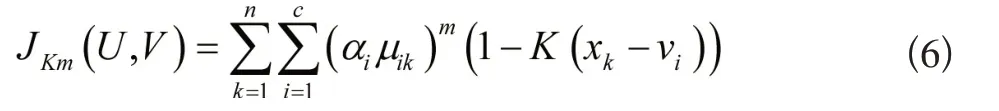
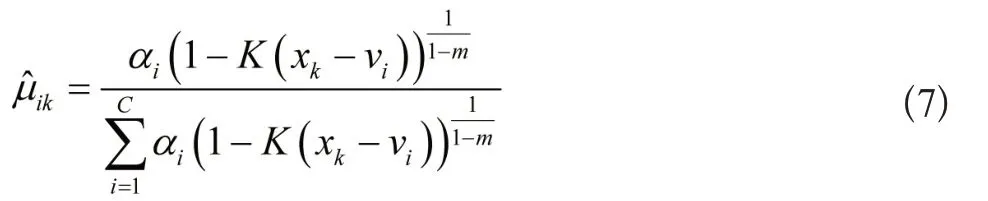
2.1.2 异常数据识别

根据所获取的聚类中心矩阵与分类矩阵，识别异常数据。神经元层作为超级神经元网络模型的第一层，主要用于分割样本数据空间，假设各神经元为(Ai，Ci)，其中，神经网络向量空间的特征矢量Ai，吸引域用Ci界定。网络模型的M个神经元节点与神经元层的K个神经元节点为全连接状态，利用下列表达界定对应权重：

公式(8)中，m=1，2，…，M，k=1，2，…，K。

将边坡变形数据分成P类，用X1，X2，…，XP表示，识别流程描述如下：

(1)超级神经元网络模型的输入设定为特征曲线X1，样本输出Y=(0，…，0)；

(2)在特征曲线Xi的首个分量中引入差值e，得到含有坏数据的新矢量，则样本输出为Y=(1，0，…，0)；同理获得全部分量叠加偏差，构建正偏差样本集合；

(3)用-e替换偏差e，重复上步流程，得到负偏差集合，结合正偏差集合，组成网络模型的全部数据样本集合；

(4)在模型中输入待测数据集合，若含有坏数据，则输出趋近于1，否则，趋近于0。

2.1.3 数据修正

当边坡变形数据经过聚类分析与识别后，需实施修正处理，保证边坡结构稳定性的准确评估。

若曲线xj上的点t1与点t2之间存在坏数据，vi1与vi2分别是两点对应的类别中心，则数据修正可通过下列修正公式实现：

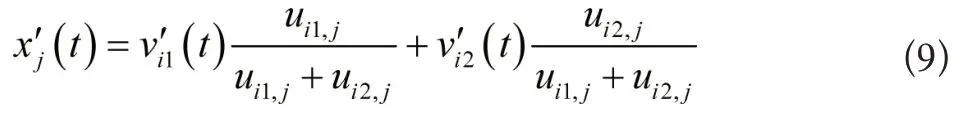
公式(9)中，t[t1，t2]，数据向量xj对类中心vi1、vi2的隶属度值分别是(t)与(t)，表达式分别如下所示：

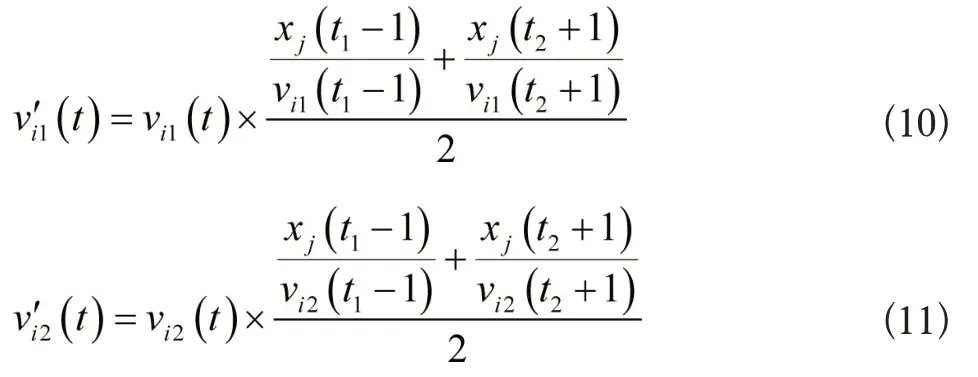
经过修正后的曲线xj，令数据集与相似类别具有更高的拟合度，尽管判定正常数据为坏数据，但修正后也不会对自动评价结果造成不良影响。

2.1.4 平滑处理

完成边坡变形数据修正后，把信号所有频率拆分到不同频带中，完成滤波、信噪分离以及特征提取。图1所示为该矿区区段的大数据预处理结果。

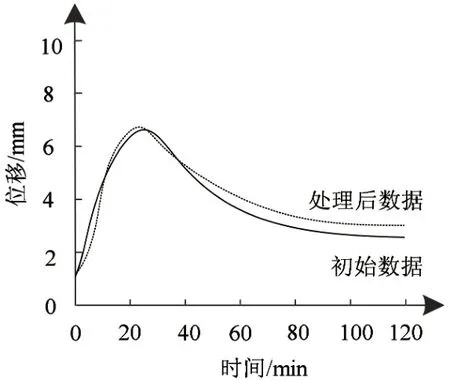
图1 坏数据降噪处理对比示意图

图1是某一时段中位移传感器的采集数据处理结果，该区段数据很有可能是传感器受到了外界因素干扰，造成了突发噪声问题，经过有效滤除噪声，真实反映出边坡结构稳定性的实际情况，发出正确的预警信号。

2.2 自动评价模型实现

在边坡稳定性自动评价搜收集大数据预处理的基础上，且因边坡失稳形式众多，将边坡稳定性自动评价转换成单分类问题，可精准判定边坡稳定性，及时发出预警信号。一般情况下，大多数样本数据属于正常类别，当数据偏离正常数据模型时被认为是异常类别。

假设自动评价模型的最优目标函数为f：X→Y，针对已知的xiX，都有一个输出yiY与之相对应。依据经验风险最小化原则[7]，得到下列最优自动评价目标函数表达式：

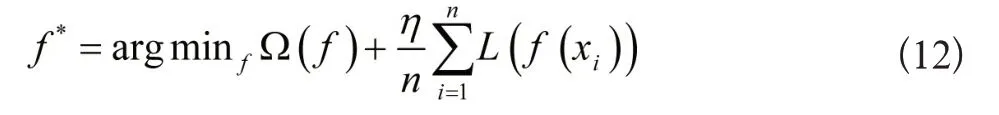
公式(12)中，损失函数为L，函数的正则化项为Ω，调和参数为η。

假设单分类支持向量机模型的半径是R，中心是χ，含有全部正常数据的超球面，则根据样本数据与球心特征空间之间的距离，对该样本数据的异常程度进行判定，其中，样本数据与球心特征空间的间距可采用下列计算公式求解：

如果样本数据位于超球面中，自动评价函数f(x)＜0，则判定该数据属于正常样本；相反，则为异常样本。因样本数据集合的噪声不可避免，故利用松弛变量ξi＞0 防止模型出现过拟合现象，数据需满足下列约束条件：

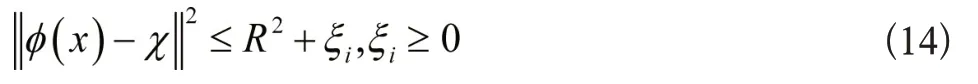
修正目标函数的同时需满足下列约束条件：

公式(15)中，平衡超球面半径与松弛变量参数用C表示，用于预估样本数据集的不纯净度。

采用拉格朗日乘子法计算该凸优化问题，表达式如下所示：

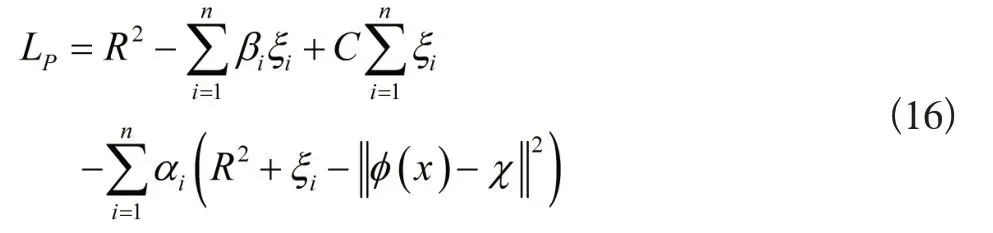
公式(16)中，αi≥0，βi≥0。求偏导R、χ 以及ξi，得到下列表达式：

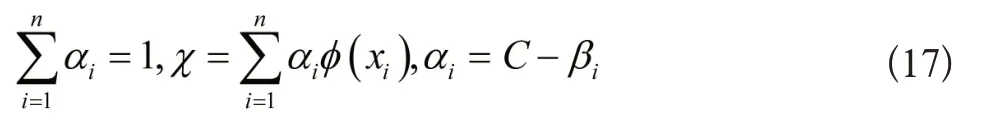
依据αi的数值大小，划分样本数据为正常数据、支持向量数据以及异常数据，对应的αi取值情况分别是αi=0、0＜αi＜C以及αi=C。

将岩体变形破坏判据设定为摩尔-库伦屈服准则[8]，利用下列公式界定稳定性参数：

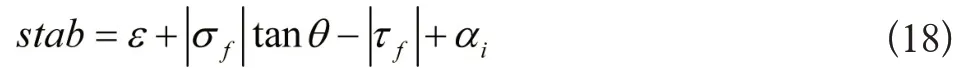
3 实验验证

选取某境内的一个矿山作为边坡稳定性研究目标，作为我国铁矿石资源的重要基地之一，该矿山的年生产量高达1538万吨，在不断增加生产需求的过程中，矿业公司对北采场展开了扩帮工程，坑底标高持续下降，当实际边坡的最大垂直高度大于一定数值时，势必会直接影响边坡的正常稳定性。

矿区位于复向斜褶皱带的东北段，复向斜的组成部分为北山向斜、南山向斜以及一个背斜，呈W 形[4]。依据地层岩性、边坡、岩体变形破坏分类等因素，划分矿区边坡为不同区段，反映不同区域的边坡特征。图2所示即为该矿区实际工程条件下工程地质区域划分示意图。

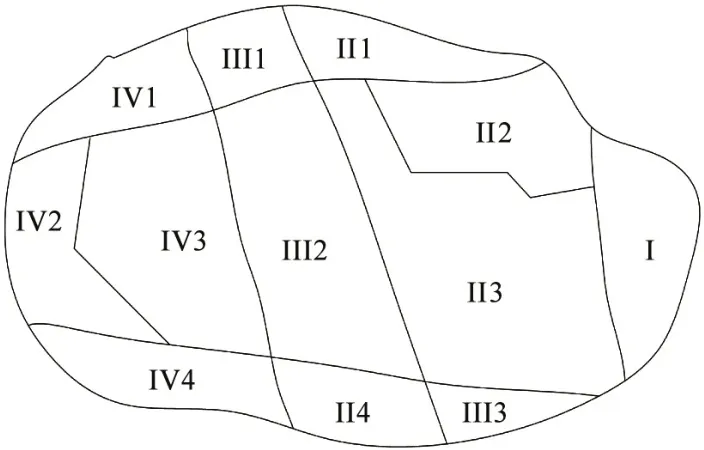
图2 边坡工程地质分区图

图2中的区段位置在北区采场下盘北面中部，标高最大值是186m，开采标高的最小值是-290m，边坡总走向是东北向，中部存在轻微变化，台阶坡面角是73°，单台阶高度是17m，总体边坡角约为43°，该区段属于断层发育，对深部边坡的稳定存在严重威胁。

在矿山边坡放置三个传感器，选取采集的近一个月数据作为自动评价模型的数据依据，根据下列治理原则进行实验验证。

图3为经过数据预处理的864 个有效数据集自动评价结果。

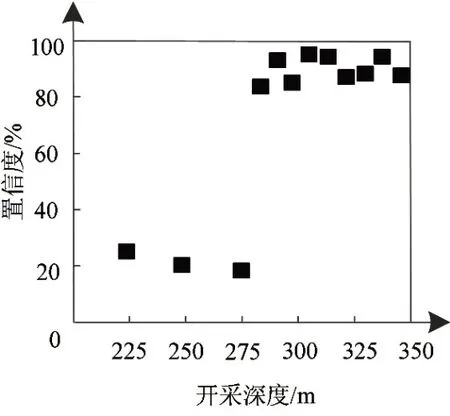
图3 有效数据集自动评价结果

通过图3可知，当开采深度为225m、250m以及275m时，置信度较低，均在30%以下，数据存在结构异常状态，表明该矿区的部分区域存在失稳威胁。而在其他区域置信度较高，在80%以上。

根据图4所示的数据采集情况，发现在第345 个时间点与562个时间点上，该矿区发生了局部的轻微失稳现象。

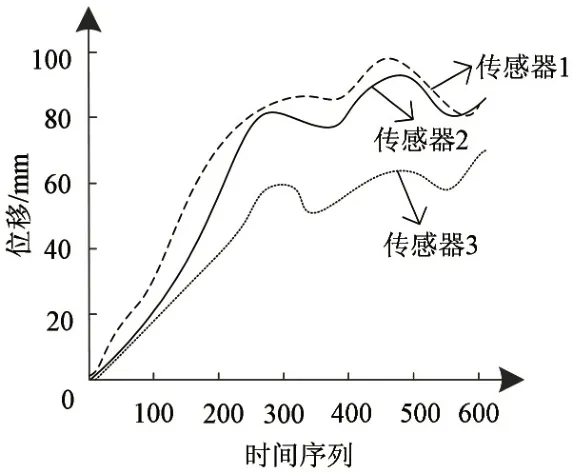
图4 基于时间点的失稳评估示意图

4 结束语

本文基于大数据环境，对矿山边坡稳定性自动评价模型展开研究。在今后的研究工作中，需进一步丰富边坡自动评价模型的内涵，采集更多的数据完善自动评价模型的可靠性；根据大数据分析边坡稳定性只是矿山开采工程的其中一个研究方向，应探索更多、更好的算法与模型，深入指导采矿作业的开展。