基于人工鱼群算法的代数方程组参数迭代求解＊

郭煜

（陕西邮电职业技术学院，陕西 咸阳 712000）

1 引言

代数方程组参数迭代求解的研究背景具体如下：代数方程组的相关问题及其求解一直是一个重要而又基础的问题[1]。这是由于在多个领域包括动力学、信息安全学、经济学、工程技术学等领域，很多实际问题的解决最终都需要转化成代数方程组的求解问题，其中较为常用的是非线性多变元代数方程组[2]。对实系数高次代数方程组的根进行求解，对综合设计以及分析控制系统有重大意义；在很多实际应用与数学理论中，求解代数方程组则是一个基础的步骤[3]。对于代数方程组参数迭代求解的研究，近年来，很多学者都将具备高度全局性、并行性、鲁棒性、适应性的算法引入了代数方程组参数迭代求解方法的研究中[4]。国内外已有相关学者提出了代数方程组参数迭代求解方法。Praks P 等人提出基于蚁群算法的代数方程组参数迭代求解方法，主要通过蚁群算法实现代数方程组的参数迭代求解[5]。王晓雷等人提出基于支持向量机的代数方程组参数迭代求解方法，主要通过支持向量机算法及人工神经网络实现代数方程组的参数迭代求解[6]。

由于在利用以上方法进行代数方程组的参数迭代求解时，在迭代次数为20次-90次的范围内存在求解速度较慢的问题，因此将人工鱼群算法引入代数方程组参数迭代求解中，提出基于人工鱼群算法的代数方程组参数迭代求解方法。

2 设计基于人工鱼群算法的代数方程组参数迭代求解方法

2.1 构建代数方程组模型

将代数方程组中包含的方程组个数设为n个，也就是求解中涉及的未知量个数为n个，构建代数方程组模型[5-6]如式(1)：

式(1)中fn(X)=An代表多元代数方程；X代表代数方程组内的未知向量集合，其表达式具体如式(2)所示；An代表代数方程内的常数项[7]。

式(2)中xn代表未知向量集合中第n个未知向量。

令下式成立：

式(3)中i代表正整数；F(X)代表代数方程。

则代数方程组参数迭代求解问题即可转化为求X使代数方程具备最小值的一种优化类型问题[8]。

2.2 行为描述

利用人工鱼群算法对代数方程组求解中的行为进行描述，包括随机行为、觅食行为、聚群行为、追尾行为。首先对人工鱼群算法内具体人工鱼状态进行定义：利用X=[x1，x2，…，xn]表示人工鱼状态。用F(X)代表食物浓度函数，将Xi人工鱼与Xj人工鱼的距离定义为：

式(4)中di，j代表Xi人工鱼与Xj人工鱼的距离；xik代表第k群人工鱼。通过人工鱼群算法优化求X使代数方程具备最小值的问题。

对随机行为进行的描述具体如下：

将当前人工鱼的状态设为Xi，当该人工鱼为当前鱼群内的最优状态，那么采取个体最优保留策略后下一状态是：

否则下一状态是：

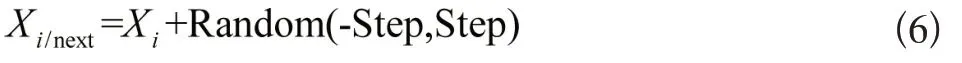
式(6)中Step代表最大人工鱼移动步长；(-Step，Step)代表实数区间；Random(-Step，Step)代表该区间中随机数构成的随机n维向量。

对觅食行为进行的描述具体如下：

将当前人工鱼的状态设为Xi，在它的可视域范围中对某一状态进行随机选择，将该状态表示为Xj，也就是二者的距离小于人工鱼的实际可视距离。当：

则表示选择的随机状态优于当前人工鱼的状态。接着使用选择的随机状态将当前人工鱼的状态替换掉，也就是：

当：

则在当前人工鱼的可视域范围中重新对某一状态进行随机选择，继续进行判断。

当试探Try_number以后还是无法满足式(7)的Xj状态，那么对随机行为进行执行。

对聚群行为进行的描述具体如下：

将当前人工鱼的状态设为Xi，在它的可视域范围中对其中的伙伴个数nf与全部伙伴的中心位置Xc进行寻找。当：

则表示中心位置Xc比当前人工鱼的状态优越。此时中心位置Xc与当前人工鱼的状态距离满足下式：

式(11)中di，c代表中心位置Xc与当前人工鱼的状态距离；Visual代表人工鱼的实际可视距离。

则下式成立：

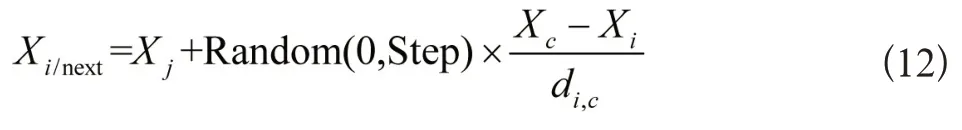
否则对觅食行为进行执行。

对追尾行为进行的描述具体如下：

将当前人工鱼的状态设为Xi，在它的可视域范围中对最优群体状态Xmin及其其周边伙伴数量mf进行寻找。当：

则表示最优群体状态Xmin比当前人工鱼的状态优越。此时，如果最优群体状态Xmin与当前人工鱼状态的距离满足下式：

式(14)中di，min代表最优群体状态Xmin与当前人工鱼状态的距离。

则下式成立：

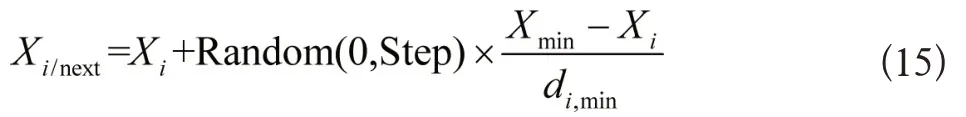
否则对觅食行为进行执行。

2.3 分段优化及终止条件

将执行人工鱼群算法的过程分成前期与后期，在前期采取较大的可视距离与移动步长，以获取较优的结果；而在后期则选择较小的可视距离与移动步长，以获取较高精度的结果，实施分段优化。在前期取的可视距离是Visualf，移动步长是Stepf。将η作为后期与前期的分界线，当分界线大于公告板时，进入后期的阶段，取的可视距离是Visuals，移动步长是Steps。

终止条件设为精度的求解值，当公告板记录符合精度求解要求则终止算法。

2.4 实现参数迭代求解

通过六个步骤实现代数方程组参数迭代求解，具体执行步骤如下：

(1)对人工鱼群算法的参数进行输入：可视距离、移动步长、群体规模、拥挤度因子、试探次数、初始人工鱼群体数。

(2)寻找当前群体内的最优状态并将其记入公告板。

(3)对公告板记录中食物浓度状态进行判断，判断其是否满足下式：

式(16)中F(XO)代表公告板记录中食物浓度；η代表群体规模。当满足则进入后期阶段；当不满足则继续此阶段中的优化。

(4)对是否符合终止条件进行判断。当满足，则对公告板记录XO进行输出并对算法进行终止；当不满足，则进入第五个步骤。

(5)分别对每条人工鱼实施追尾行为与模拟聚群行为，将最优行为当作最终执行行为。而随机行为与觅食行为则属于缺省行为。

(6)找到最优群体状态并将比较其与公告板记录。当其优于后者，则对其进行替换，并转向第三个步骤。

3 代数方程组参数迭代求解实验

3.1 实验设计

为证明设计的基于人工鱼群算法的代数方程组参数迭代求解方法的性能，对其进行代数方程组参数迭代求解实验验证。在实验中，通过Matlab6．0对基于人工鱼群算法的代数方程组参数迭代求解方法进行编程实现，使用的编程程序具体如图1所示。

图1 使用的编程程序

实验中使用的两个例子具体如下：

第一个例子：

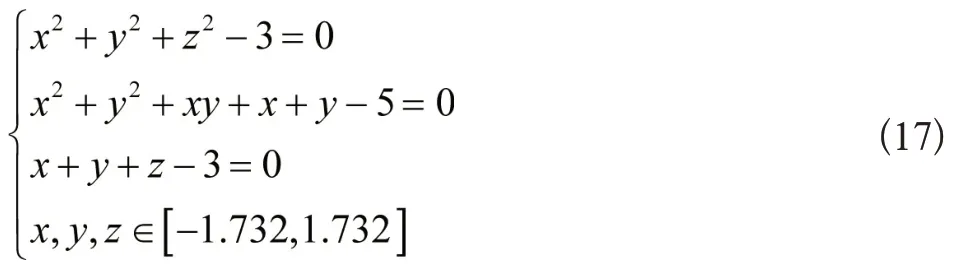
此处参数取值具体如下式：

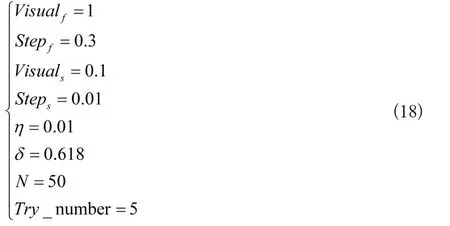
式(18)中δ 代表拥挤度因子；Try_number 代表试探次数；N代表初始人工鱼群体数。

设定的最大迭代次数是一百次。

第二个例子：

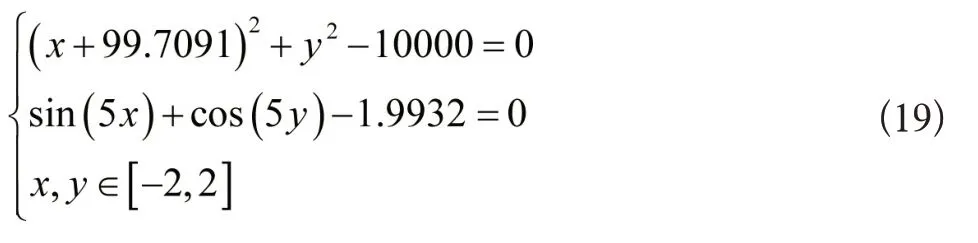
其终止条件具体如下式：

此处参数取值具体如下式：

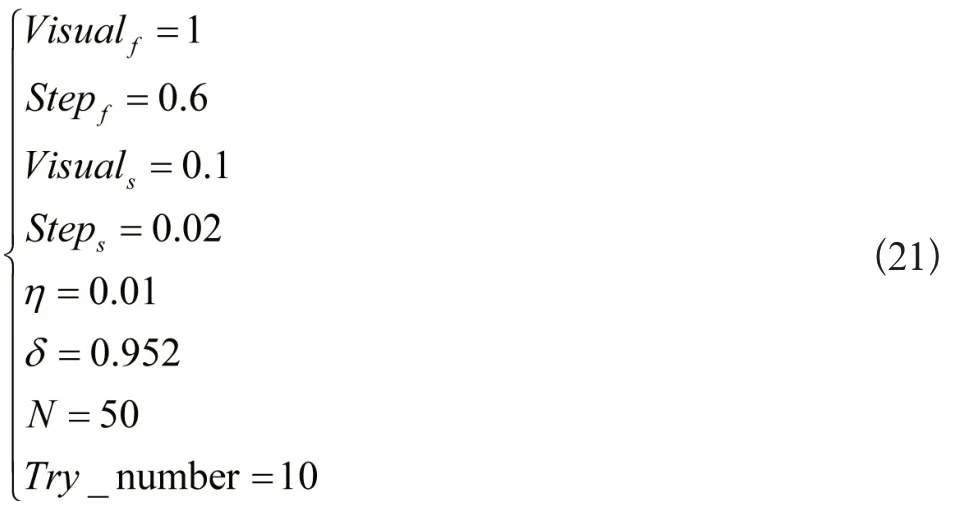
利用基于人工鱼群算法的代数方程组参数迭代求解方法对实验中的例子进行参数迭代求解。获取迭代次数为20次-90 次范围内的求解速度作为实验数据。为避免本次实验结果较为单一、缺乏对比性，将原有的三种参数迭代求解方法作为实验中的对比方法，分别为基于蚁群算法、基于支持向量机、基于人工神经网络的代数方程组参数迭代求解方法。同样利用这三种方法进行实验例子的参数迭代求解。获取迭代次数为20 次-90 次范围内的求解速度数据作为对比实验数据。

3.2 实验结果分析

在求解方程组的取值在迭代次数为20 次-90 次的范围内，基于人工鱼群算法的代数方程组参数迭代求解方法与基于蚁群算法、基于支持向量机、基于人工神经网络的代数方程组参数迭代求解方法第一个例子的求解速度对比实验数据具体如表1所示。

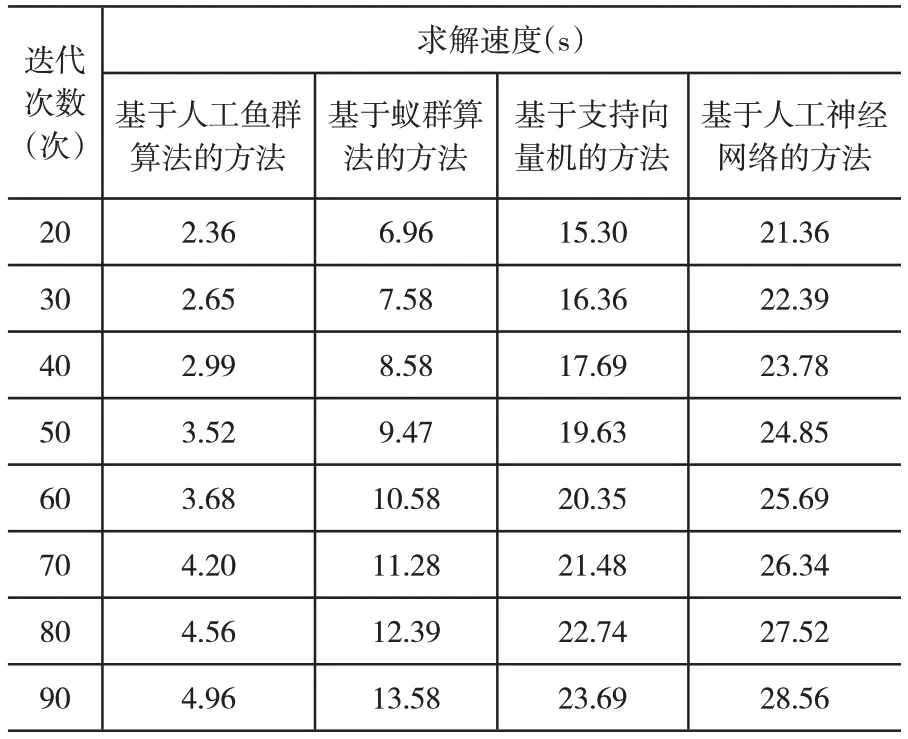
表1 第一个例子的求解速度对比实验数据

根据表1中第一个例子的求解速度对比实验数据可知，基于人工鱼群算法的代数方程组参数迭代求解方法的求解速度高于基于蚁群算法、基于支持向量机、基于人工神经网络的代数方程组参数迭代求解方法。

在迭代次数为20次-90次的范围内，基于人工鱼群算法的代数方程组参数迭代求解方法与基于蚁群算法、基于支持向量机、基于人工神经网络的代数方程组参数迭代求解方法第二个例子的求解速度对比实验数据具体如表2所示。

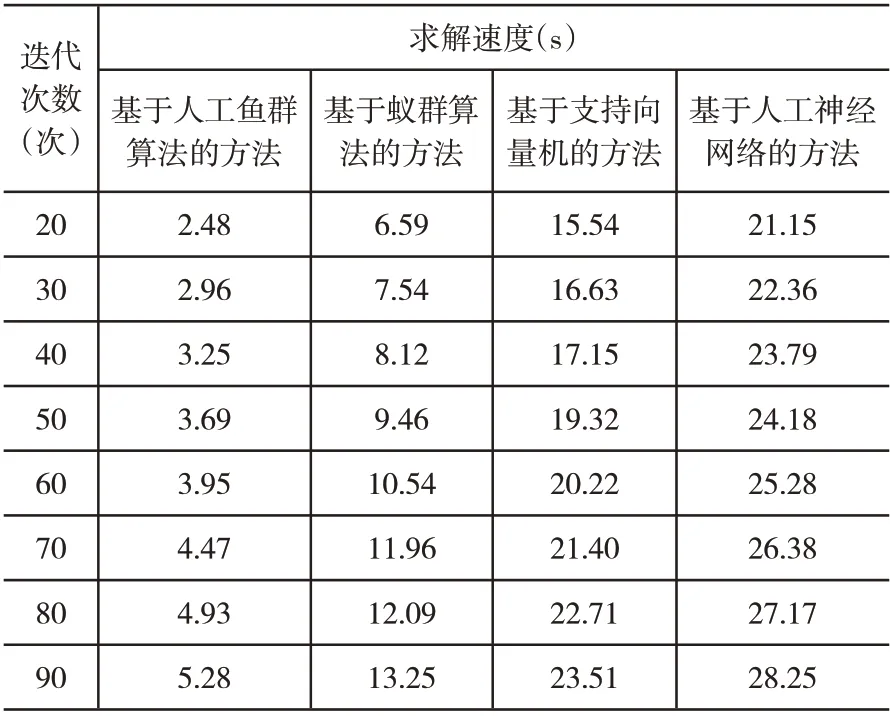
表2 第二个例子的求解速度对比实验数据

根据表2中第二个例子的求解速度对比实验数据可知，基于人工鱼群算法的代数方程组参数迭代求解方法的求解速度高于基于蚁群算法、基于支持向量机、基于人工神经网络的代数方程组参数迭代求解方法。

4 结束语

基于人工鱼群算法的代数方程组参数迭代求解方法实现了求解速度的提升，对于代数方程组参数迭代求解方法局限性的突破有很大启示意义。