基于时序数据挖掘的电价执行异常分析模型设计

路 洁,郑小贤,杨 辉,贾 蕾

（1．国网宁夏电力有限公司，宁夏 银川 750000；2．国网银川供电公司，宁夏 银川 750001）

1 引言

随着科技水平的不断发展，电力公司利用不同的检测模型、分析模型，实时监测电价中出现的电价执行异常问题[1]。电价异常主要是由两大类问题导致的，一是电力设备损坏导致数据异常，另一类是用户设备损坏或短路导致用电异常，从而引发整体电价异常[2]。为了解决这一问题，相关学者设计了一些相对成熟的电价执行异常分析过程，如基于深度学习变分自动编码器算法的电价执行异常模型[3]和基于准实时数据的电价异常分析模型[4]等。然而在传统方法挖掘的数据中，包含大量无效数据，因此模型在分析数据动态特性的过程中，很难与异常数据的动态性保持一致。针对这一问题，本研究设计了基于时序数据挖掘的电价执行异常分析模型，以期为电网用电安全、居民用电安全提供更可靠的支持。

2 电价执行异常分析模型设计

2.1 动态划分时间粒度设置时序数据挖掘规则

时间是一种既没有源头也没有尽头的指标，因此想要依靠时序数据挖掘方法设计模型，需要动态划分时间粒度，将时序数据划分成时间间隔不同的子序列，通过该序列设置时序数据挖掘规则。在时序数据挖掘过程中，时序数据就是具有时间维度的数据，因此采用统计分析法和自组织映射神经网络法动态划分时间粒度。

①统计分析法采用秩相关分析，研究数据之间的关联性，即计算数据之间的皮尔曼系数[5]。则该系数的计算公式为：

公式(1)中：Zi表示数据xi在数据集X中的秩；Wi表示数据yi在数据集Y中的秩；P表示皮尔曼等级相关系数；n表示数量。通常情况下，P的取值范围在(-1，1)之间，若存在-1＜P＜0，说明两个变量存在负相关关系，也就是说两个变量的变动方向，完全相反；若存在0＜P＜1，说明两个变量存在正相关关系，即两个变量的变动方向一致；若|P|=1，说明变量之间具有函数关系；若|P|=0，说明变量之间无关联。

②自组织映射神经网络，是一种特殊的网络模式，可用于数据聚类和可视化，并从海量的数据中找出隐藏的数据信息。采用自组织映射，将所有电价原始数据整合到一起，按照数据类型划分区域，找出每个区间内的最小化个体差异，同时保证每个区域的差异最大化[6]。该过程具体实现步骤如下：

根据输入节点到输出节点的所有权值，设置一个小的随机数，同时令时间计数t=0，初始化连接权值。设置网络输入模式，令。计算输入节点与输出结点之间的欧氏距离，公式为：

公式(2)中：lj(x)表示第j组节点之间的欧氏距离；L表示样本维数；ωji表示输出与输入节点之间的连接权值。根据上述计算，得到的最小欧氏距离的输出结点获胜。调整输出结点的连接权值，同时调整输出节点在邻域内的权值。公式为：

公式(3)中：S(x)表示获胜结点；Dj，S(x)表示更新节点距离；δ表示方差。根据上述分析，最后计算映射权重，公式为：

公式(4)中：μ(t)表示可变学习速度，该值随着时间的增加而减小[7-8]。若还有输入样本数据，则重新设置网络输入模式进行迭代，直至收敛。上述计算过程中，统计分析过程就是按照数据属性划分数据，而自组织映射就是用简单的网络形式，表现复杂的数据分布特征。而时序关联规则，是挖掘时序数据过程中的一项限制条件。因为时间序列本身具有波动行为，因此在动态划分时间粒度的前提下，设置时序数据挖掘规则。

当计算结果存在F()＞1 时，认为规则为有效的强规则；当F()＜1 时，则认为规则为无效的强规则；当F()=1时，表示序列X和序列Y之间是相互独立的，即X的出现没有影响序列Y。至此在动态划分时间粒度的基础上，完成对时序数据挖掘规则的设置。

2.2 挖掘电价执行异常时序数据

根据上述设置的挖掘规则，挖掘电价执行异常时序数据。该过程采用二元正态密度核函数，计算任意电价区间内，单元格的密度估计值，公式如下：

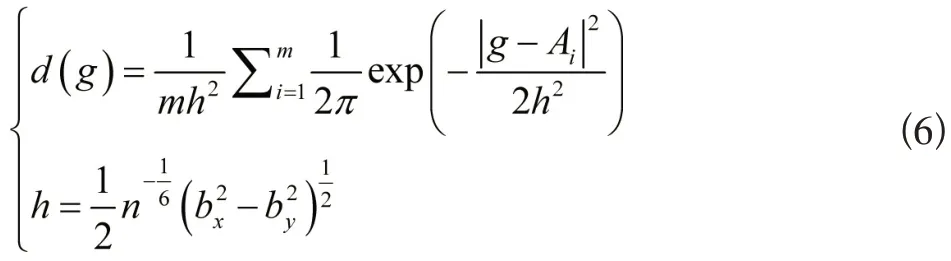
公式(6)中：d(g)表示密度估计值；m表示时序数量；h表示动态时序数据，移动轨迹光滑参数；Ai表示动态时序数据的活动坐标；|g-Ai|表示表示单元格g和活动坐标Ai之间的距离；bx、by分别表示电网分布式价格变动区域，动态时序电价的移动轨迹中，所有位置点对应的横坐标和纵坐标标准差[9-10]。根据上述计算，将电网价格中，出现电价执行异常的区域，视为近似单元格连成的区域，该区域的判别公式为：

公式(7)中：d(g1)、d(g2)表示电网中两个相邻的单元格，组成的电价区间密度估计值；σ表示异常区域判断阈值。按照上述步骤挖掘异常区域后，还要进一步挖掘异常区域内，动态时序数据的活动规律，完成对整个电网价格中，所有存在执行异常的数据序列挖掘。因此假设任意一个动态时序数据为Ui，任意一个异常区域为Cj，则二进制序列为V=v1，v2，…vk，其中vkV，当vk=1时，说明动态时序数据在k时刻时，访问了异常区域Cj；当vk=0 时，则时序数据没有访问异常区域。离散傅里叶变换上述提出的二进制序列，得到该序列的频谱序列函数：

公式(8)中：k/M表示离散傅里叶级数的系数，捕捉到的动态变化频率；M表示序列总数量；i表示虚数单位。根据上述计算结果，计算电价执行异常的区域图像：

为避免出现虚假预警的问题，引入自相关函数检验上述计算结果，确定电价异常区域中，动态时序数据的变动周期，该函数的公式为：

公式(10)中：τ表示随机数据。通过上述计算过程，完成对电价执行异常时序数据的挖掘。

2.3 设计电价执行异常分析模型

已知用电数据异常的表现包括：线损高、售电量损失大等，其中线路及设备质量、管理漏洞、电能表质量以及异常用电，都是导致线损过高的主要原因。而无论出现何种情况，用电执行异常都需要通过电表进行反馈，因此通过构建日负荷曲线，设计电价执行异常分析模型。从用电信息采集系统中，选择用户初始用电负荷数据集的所有关键字段，内容如表1所示。

表1 用户初始用电负荷的数据字段

已知电网控制系统使用的终端为96 版本，因此该系统只能采集用户电能表，在零点时刻的电流电压以及用电数据。为了便于设计分析模型，将96 点负荷数据，转变为24点，即将数据集合，由n条日负荷曲线，构成n×24阶的初始负荷曲线矩阵。清洗数据挖掘得到的基本数据，该过程首先总结脏数据类型，按照其表现形式采用合理的清洗手段。归纳整理分类结果如表2所示。

表2 分类处理后的脏数据类型

根据表2的分类结果，首先删除挖掘数据中的重复数据；然后根据实际情况，补充存在缺失的数据，保持数据集的完整性。若数据缺失现象十分严重，则利用下列公式修补缺失数据：

公式(11)中：c1、c2分别表示前推期数和后推期数；t表示负荷数据缺失所处的时刻。因此根据上述处理，构建(n-q)×24阶有效负荷曲线矩阵。完成上述计算后，建立电价执行异常分析模型，检测用户用电时，电价执行是否存在异常问题，判断用户是否为异常用户。

综上所述，在时序数据挖掘技术的应用下，电价执行异常分析模型设计完毕。

3 测试与分析

为验证基于时序数据挖掘的电价执行异常分析模型的设计应用性能，进行仿真测试。比较不同分析模型对异常电价的判别差异。为避免测试结果的单一性，将本文模型作为实验组，将传统的基于深度学习变分自动编码器算法的电价执行异常模型作为对照A组，将基于准实时数据的电价异常分析模型作为对照B组，共同完成性能验证。

3.1 实验准备

实验测试过程应用的主要设备有台式计算机、信号传感器、信号接收器和信号采集器。以W地区的电价为例，搭建Matlab仿真测试环境。表3为测试地区的日常使用电价。

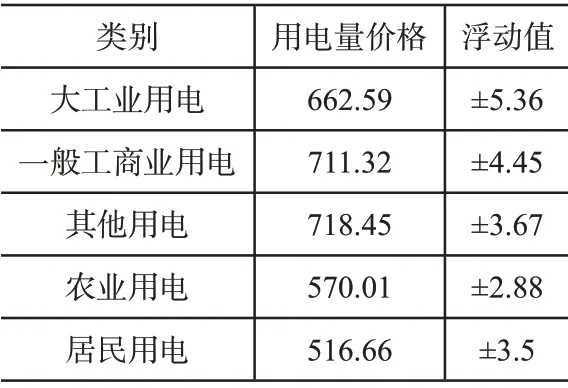
表3 测试地区用电价格统计(元/WMh)

基于此，连接各实验设备，以表3中的数据为参照，模拟W地区的电网用电场景，然后分别利用三种模型分析电价执行异常的现象。

3.2 结果与分析

为了使实验结果更加真实、更有说服力度，将用电异常比例分别设定为30%、15%以及5%，然后仿真测试软件共模拟三个不同的电价执行异常的场景，对比不同模型对用电异常的分析结果，如图1所示。

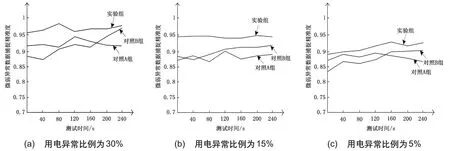
图1 不同用电异常比例下的分析效果对比

根据图1中的测试结果可知，当用电异常比例为30%时，实验组模型在神经网络的帮助下，通过映射捕捉到了微弱的异常数据。而两个对照组中的模型在面对海量的异常数据时，模型捕捉异常数据的能力较差，导致其对微弱异常数据的捕捉精准度低于实验组模型。随着用电异常比例的降低，不同模型的微弱异常数据捕捉精准度逐渐减弱。当用电异常比例下降到5%时，两种传统模型由于深入分析的能力不够，未能找出海量数据中隐藏的异常数据，因此其对微弱异常数据的捕捉精准度始终低于实验组模型。同时可以发现，尽管用电异常比例在不断下降，但实验组模型的捕捉精准度始终处于90%以上，由此可以证明本文方法在分析电价执行异常过程中具有更高的应用优势。

4 结束语

本研究设计了基于时序数据挖掘的电价执行异常分析模型，并通过实验测试证明了该模型的有效性。在今后的研究工作中，将考虑设计一个数据挖掘算法，在数据挖掘环节中，通过降低错误挖掘概率进一步提高模型的应用性能，为国家维护电价、用户维护自身的用电权益提供更加高效的支持。