基于受限玻尔兹曼机的医疗建筑施工轴承故障定位技术研究

罗鸿宇

(四川大学华西医院，四川 成都 610041)

1 引言

受限玻尔兹曼机作为一种能够使用输入数据集，可实现学习概率分布，继而生成随机神经网络。在协同过滤、主题建模、分类以及降维内、特征学习中被广泛地应用，同时，能够依据任务的不同，还可以应用于无监督的学习方法或者监督的学习方法中，完成训练。而轴承作为现代机械的一种重要零件，它的主要目的是对机械的旋转转体运动连接进行支持，进而减少运动过程的摩擦，保证回转的精度。轴承一旦出现故障，就会令机械设备出现隐患、甚至伤及人体安全，随时发生危险。所以需要在对轴承故障位置进行检测定位时，通过引入受限玻尔兹曼机方法，提升定位精度。

魏乐等人传统轴承的故障诊断定位方法，多数是通过人工的方式进行特征提取，这样就依赖于复杂信号的处理方法和人工专业的知识经验[1]。所以利用改进深度的信念网络，实现故障诊断定位。齐咏声等人提出变分模态分解以及熵价值滚动轴承的诊断定位方法，先将起始信号进行分解，利用熵价值法筛选出存在故障信息最多的模态，然后计算对应模态能量熵和其能量组成复合的特征向量，以此来作为振动信号特征的向量，最终构建叶贝斯准则最小的二乘支持向量机分类器实现故障诊断定位[2]。

上述方法虽然能够有效地进行轴承故障定位，不过在实际应用的过程中，由于应用的范围比较小，很难满足于医疗建筑施工的轴承故障定位。为此本文提出一种基于受限玻尔兹曼机的医疗建筑施工轴承故障定位技术，该方法通过分别计算轴承的外圈、内圈和滚动体故障的特征频率，利用自相关函数区分故障信号，完成精准定位。

2 受限玻尔兹曼机训练

受限玻尔兹曼机作为一种关联两个无向图模型马尔可夫的随机域，其具体结构如图1所示。

通过观察图1能够看出，受限玻尔兹曼机包括隐含层单元以及可视单元，其中，m维可视层单元代表轴承的观测数据，n维隐含层单元主要用于获得观测轴承变量之间的依赖特性，从而确认轴承是否出现故障[3]。

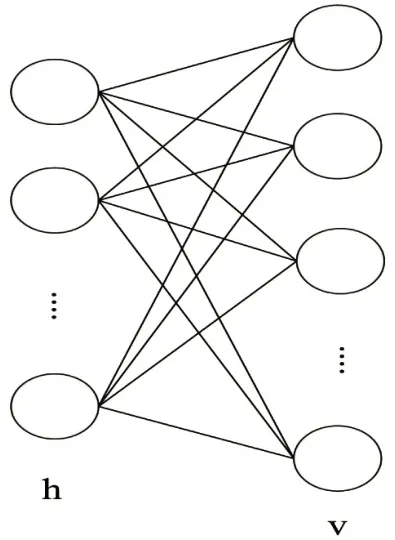
图1 受限玻尔兹曼机的构造示意图

在二值的受限玻尔兹曼机内，它的随机变量(V，H)取值范围为(v，h)∈{0，1}m+n，而模型的联合分布概率通过吉布斯分布确认，具体能量函数公式为：

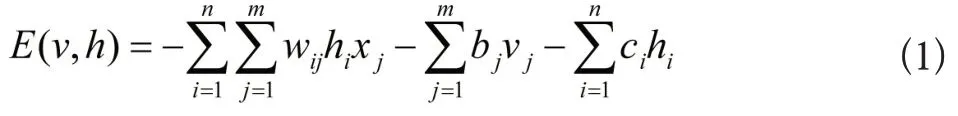
相对于全部i∈{1，…，n}以及j∈{1，…，m}，wij代表实值权值和单元Vj以及Hi之间的关联。并且bj与ci代表实值偏置项分别和第j个可视变量以及第i个隐含变量的关联[4]。给定的可视层状态以及隐含层的互相独立，具体概率公式为：

对于隐含层的单元之间无连接构造令隐含变量边缘的分布容易计算，具体可以获得公式为：

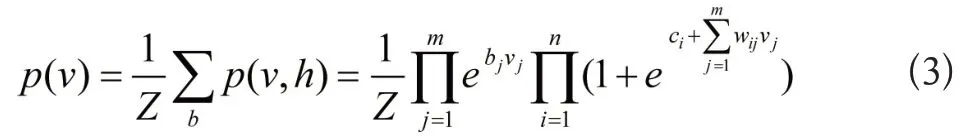
式中将独立构成部分，利用乘积的方式进行组合，所有上述的分布，都能够随意的利用m个可视层以及k+1个隐含层的受限玻尔兹曼机进行建模，而其中k代表目标分布所支持的集基数，就是存在非零观测概率输入的元素数量[5]。受限玻尔兹曼机存在独立变量的条件，按照其概率，可以被看成是随机神经元激活的概率，而激活的函数σ(x)=1/(1+e-x)，具体可以获得公式为：

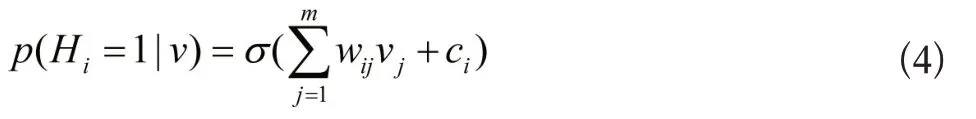
将表示V-1为可视单元之外的全部可视单元状态，具体定义公式为：

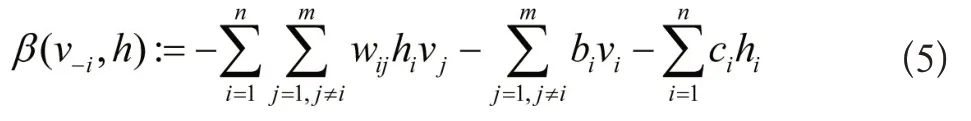
对于相同层的变量之间，它们的独立性会令吉布斯的采样过程出现极大程度的简化：通过对全部变量的新状态进行连续采样，相同层中全部变量的状态能够同一时间进行采样获得。所以，受限玻尔兹曼机吉布斯的采样仅需要实现两个主要的步骤：它们分别是基于条件概率p(h|v)对于隐含单元的新状态h采样，以及基于条件概率p(v|h)能够对于可视的单元新状态v采样。这个过程是吉布斯采样。而受限玻尔兹曼机能够认为是包括一层非线性的处理单元前馈性神经网络。受限玻尔兹曼机构成一个准确函数{0，1}m→Rn，把输入v∈{0，1}m，利用yi=p(Hi=1|v)映射至y∈Rn，就是在给定观测之下，具体数据会被映射至期望隐含的神经元状态内[6]。

3 医疗建筑施工轴承故障定位技术

3.1 轴承的故障特征计算

因为医疗建筑施工区域存在环境噪声，而轴承的振动信号在运行的过程中，会受到剧烈的影响，这些外界的噪声，在通常情况下会表现成高斯白噪声n(t)，其幅度的分布要服从于高斯分布，所以具体平均能量是零，同时功率谱的密度也是均匀分布的[7]。

假设轴承的外圈处于固定状态，而内圈是与轴承一起运动的，轴承转频是fr，利用S(t)代表故障信号，具体公式为：

上式中：d(t)代表轴承的故障脉冲函数。

上式中：d0表故障的程度，δ(t)代表脉冲函数，f代表对应故障的频率特征[8-9]。

而为了便于定位计算，假设轴承的外圈是处于固定状态，旋转的频率是fr，直径是D，滚动体的数量是z，接触角是α，而滚动体直径是d，且假设滚动体和内外圈间是理想纯滚动。由于外圈为固定的，获得滚动体上B点速度为0，而A点的速度为，以此能够获得公式为：

上式中：fc代表滚动体公转的频率。

将滚动体自转的频率设置成fb，那么可以利用下列方法进行推导，在整体轴承的系统上通过添加一个大小是fc旋转角速度。在保持架绝对地静止，因此外圈会以fc频率进行旋转，而滚动体的角速度依旧为fb，依据现有的力学理论基础，可以获得公式为：

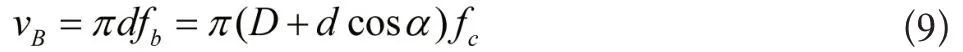
以此能够得到公式为：

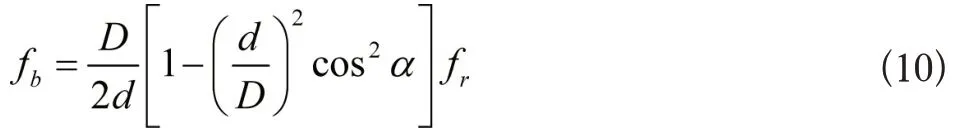
以此能够推导出故障的频率：

(1)轴承的外圈故障特征频率公式为：

(2)轴承的内圈故障特征频率公式为：

(3)滚动体故障的特征频率公式为：

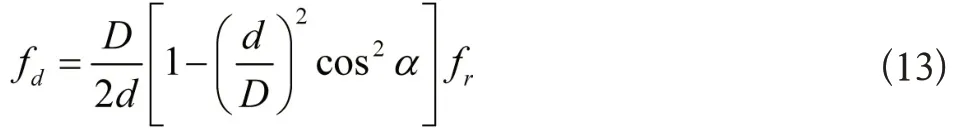
上式中：f0、fi以及fb分别代表轴承的外圈、内圈和滚动体故障的特征频率。

3.2 轴承故障定位

在设置x(t)为各态历经的随机过程样本记录，x(t+τ)为x(t)时移τ后样本记录，明显x(t)与x(t+τ)存在一样标准差以及值，即各态历经过随机的信号能够定义相关的函数Rx(τ)公式为：

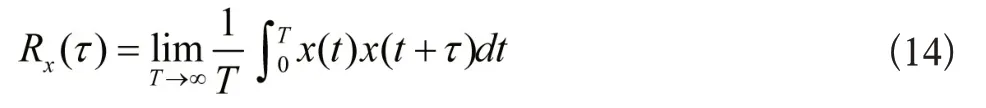
自相关的函数作为区分信号种类的手段。对于信号内只要包含周期分量，那么其自相关的函数处于τ较大时不会减少。且存在显著周期性，同时，也不会有随机信号的情况发生，在τ增大时，其自相关函数则会趋近于0，宽度随机的噪声，其自相关函数会极快衰减，变成0，而若是随机噪声，那么自相关函数衰减特性则会非常慢。

而互相关函数Rxy(τ)通常用来对两个信号处于不同时刻互相依赖关系进行分析。而具体对于各态历经过程随机信号x(t)以及y(t)相关Rxy(τ)能够定义公式为：

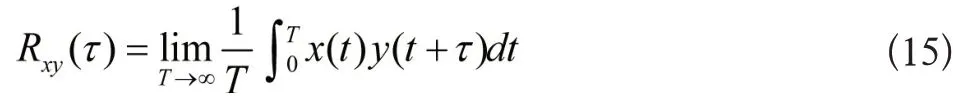
如果x(t)与y(t)两个信号的频率周期成分或者相周期信号频率一样，当τ→∞，则互相关函数收敛情况不会发生，同时，该周期成分的频率会发生。反之，这两个信号频率是不一样的周期成分，即两者之间没有关系。

将振动或者是噪声信号x(t)利用一个非频变线的路径传递，在传递的过程中加入噪声n(t)，最终能够获得结果为y(t)。

如果传递路经增量的因子是常数a，而传递的路经距离是d，信号的传输速度是c，那么具体公式为：

计算x(t)和y(t)相关函数公式为：

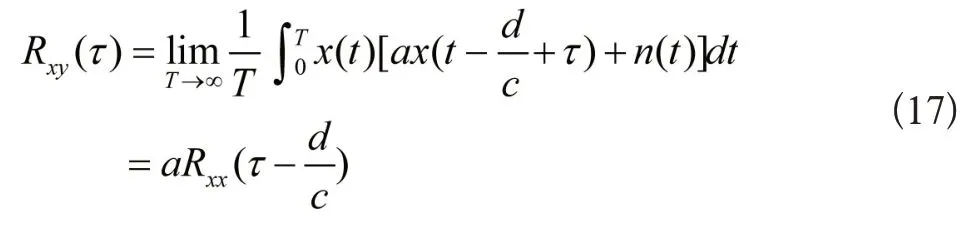
以此看出相关函数Rxy(τ)能够利用x(t)自相关函数进行代表，而在互相关的图中，峰值一定会发生在位置，所以知道速度c或者距离d，就能够从互相关的图像中，获得时差τ0，进而计算出d或者c，以此即可完成医疗建筑施工轴承故障定位。

4 实验仿真证明

4.1 实验数据

为了验证本文方法的有效性，采用SQI-MFS 实验平台的轴承故障振动数据进行测试实验，本节采用一种医疗建筑轴承处于转速下的振动数据来作为训练集样本，在使用不同的医疗建筑轴承振动数据作为测试集样本。为了更好地进行观察测试，利用医疗建筑轴承的转速处于1000tr/min 下的数据来作为测试样本，而训练样本则使用2000tr/min 数据。具体的实验数据表，如表1所示。

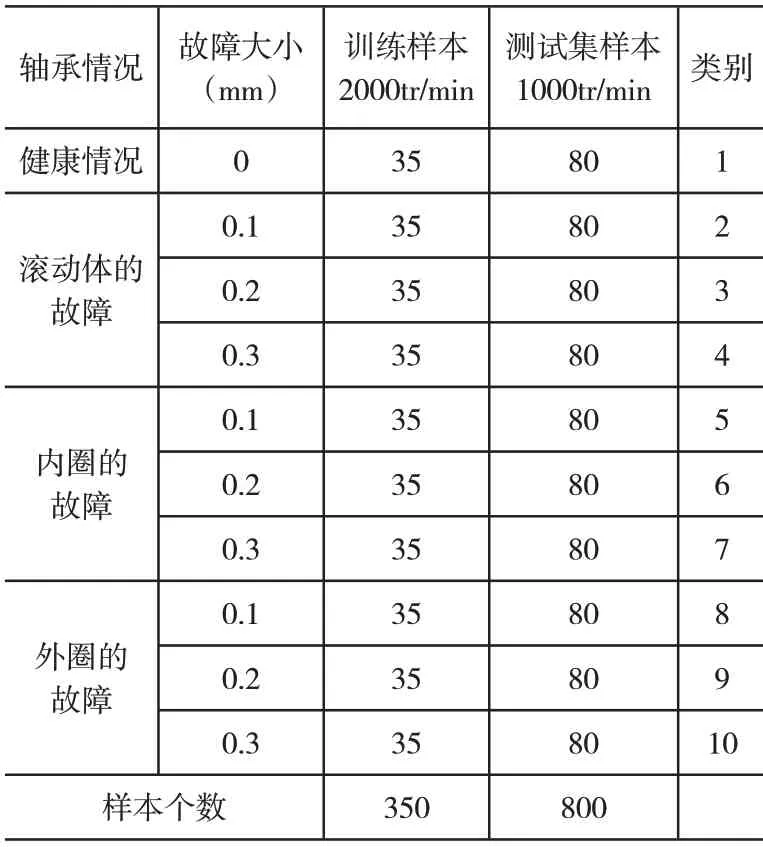
表1 实验环境数据表

在对滚动轴承的正常状态、内圈的损坏状态、外圈的损坏状态以及滚动体的损坏情况进行监测，以峭度、波形因子、裕度因子、脉冲因子以及峰值因子作为标准，观察轴承的故障情况，是否满足应用条件，具体方案的验证样本如表2所示。

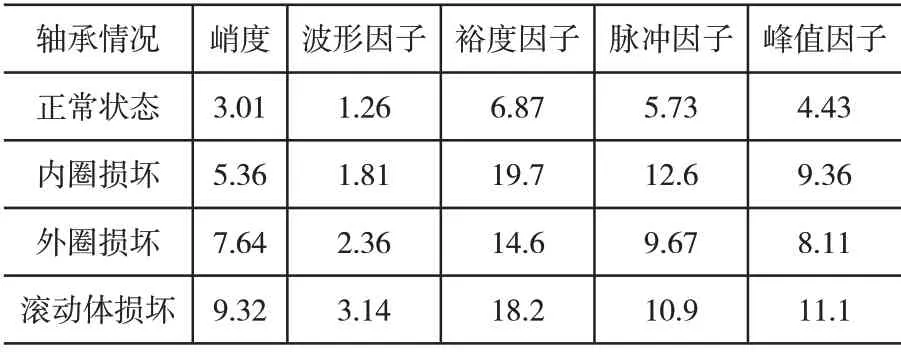
表2 具体方案的本文方法验证样本

4.2 实验结果分析

为了明显观察出本文方法的故障定位效果，将与理想情况进行对比，具体结果如表3所示。

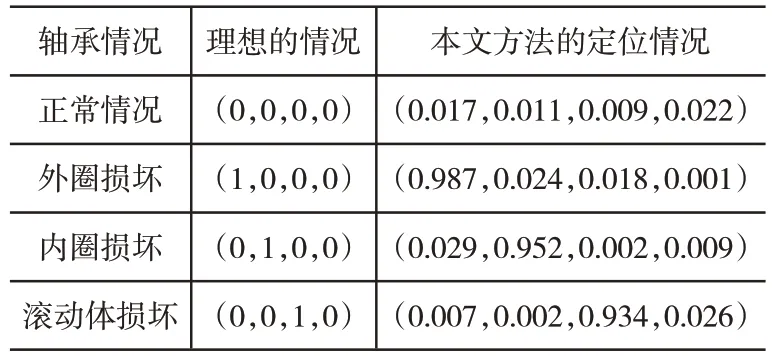
表3 本文方法定位结果

通过表3的数据对比能够得出，本文方法的定位结果与理想结果基本相同，差距甚小，这主要因为本文对轴承的故障特征进行计算，能够从优先划分可能产生故障的区域，再进行精准定位。

5 结束语

本文提出的基于受限玻尔兹曼机的医疗建筑施工轴承故障定位技术研究，与其他方法对比，定位精度较高，且计算量小，不会随着轴承故障定位数据增加，导致定位效果变差，以此证明所提方法效果良好，不过由于社会的发展，各种机械设备的出现，对于轴承的使用范围越来越广，所以本文方法未来对于轴承的故障定位要越来越精准。