改进的D-H参数下串联机器人建模与运动学分析＊

程 伟,屈福康,肖 金

（广东工业大学华立学院，广东 广州 511325）

1 引言

串联机器人工作时，一般驱动力或力矩通过关节i的轴线施加到杆i上，杆i再将相应的运动或力通过关节i+1传递给杆i+1。我们通常称关节i 的轴为杆i 的驱动轴，关节i+1的轴为杆i的传动轴[1]。Danevit 与Hartenberg 在1955年给出了一种建立与机器人各杆件固连坐标系的一种方法，简称D-H 方法[2]，现已在机器人上被广泛应用。应用D-H 方法建立串联机器人杆件坐标系的Zi轴是沿杆件i的传动轴方向，如果遇到串联机器人(树形[3]或含闭链结构[4]的机器人)某个杆件上含有多个传动轴的情况时，D-H 方法建立的杆件坐标系就会产生歧义。1986年Khalil和Kleinfinger提出一种改进的D-H方法[5]，其特点是选取杆件i的驱动轴轴向(关节i的轴向)做为杆件i坐标系的Zi轴，这样就克服了D-H方法的上述缺点。

2 传统D-H参数建模方法

串联机器人一般由若干个刚性杆件首尾通过关节相连而成。一般我们把基座称为杆0，依次向外杆件可编号为杆1、杆i、杆i+1，杆i+1与杆i之间关节为关节i。则关节i是杆i的近端，关节i+1是杆i的远端。对于n自由度机器人，其建立杆件i(i=0，1，…，n)固连坐标系OiXiYiZi的方法步骤[6]如下：第1步：选取杆件关节i+1的轴向做为坐标系的Zi轴。第2步：过Zi-1轴和Zi轴的公法线上确定坐标系的原点Oi。第3步：选取Zi-1轴指向Zi轴的公法线为坐标系的Xi轴。第4步：依据右手坐标系(Yi=Zi×Xi)确定Yi轴方向。

3 改进的D-H参数定义

当用改进的D-H方法建立串联机器人各杆件的坐标系后，坐标系i-1和坐标系i之间相对位置和指向便可用4个改进的D-H参数(ai、αi、di、θi)来描述[7](见图1所示)。

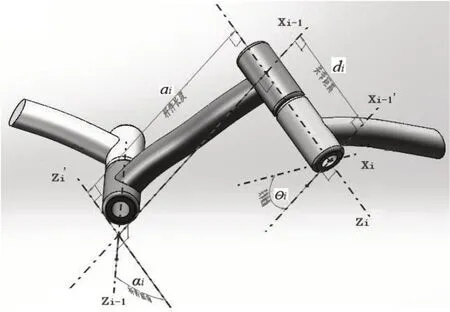
图1 改进的D-H参数空间位置关系图

①杆件长度ai定义为从Zi-1到Zi的距离，沿Xi-1轴指向为正；

②杆件扭角αi定义为从Zi-1到Zi的转角，绕Xi-1轴正向转动为正；

③关节距离di定义为从Xi-1到Xi的距离，沿Zi轴指向为正；

④关节转角θi定义为从Xi-1到Xi的转角，绕Zi轴正向转动为正。

4 改进的D-H参数下机器人运动学

用改进的D-H方法建立起串联机器人杆件坐标系的齐次变换矩阵[8]可表示为：

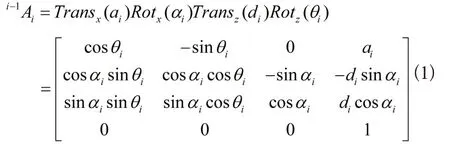
对于自由度为n的串联机器人，若其杆n的齐次变换矩阵可用其关节位置变量q表示为：

则其速度矩阵可表示为：

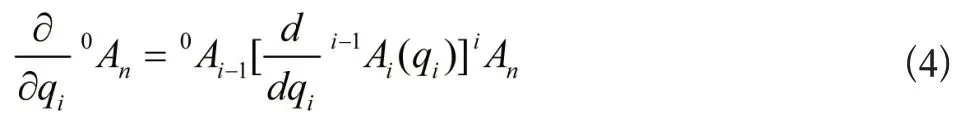
则有：

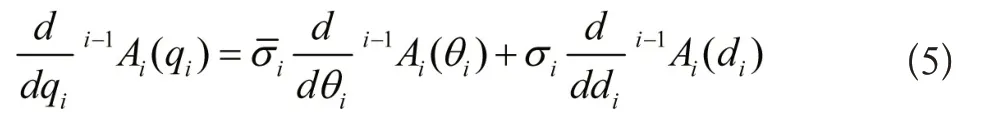
如果该串联机器人坐标系采用改进的驱动轴坐标系建立的，则由上述1式分别对θi、di求导可得[9]：

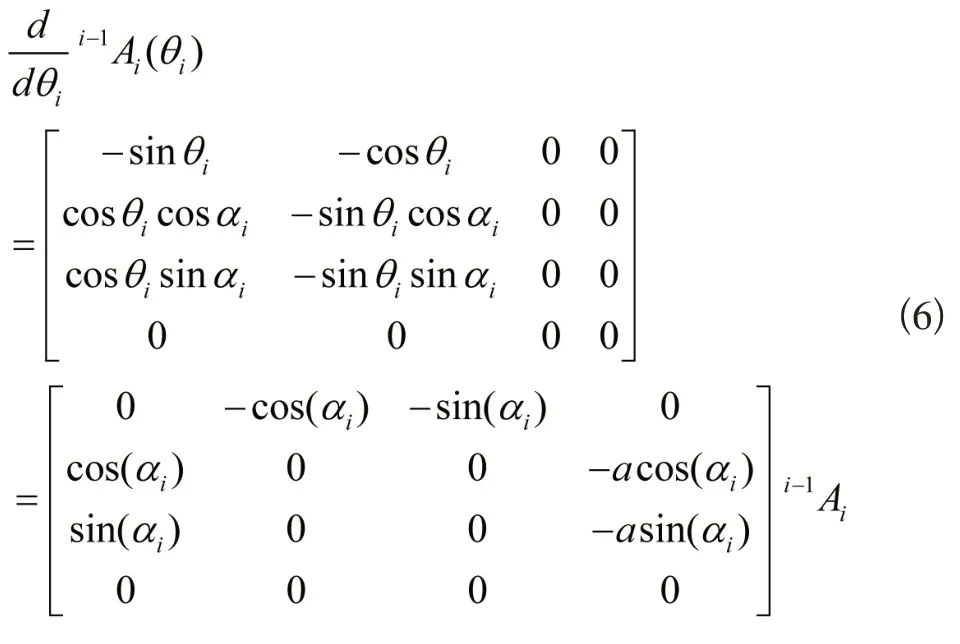
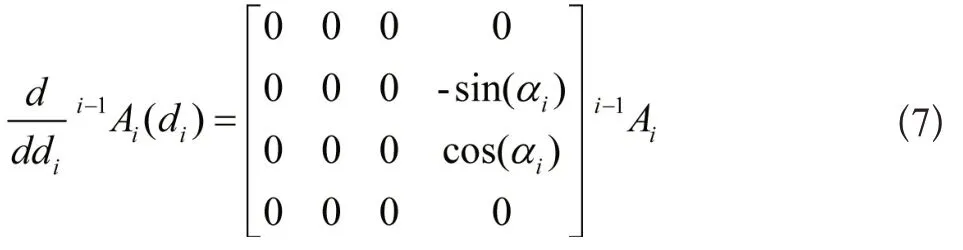
令

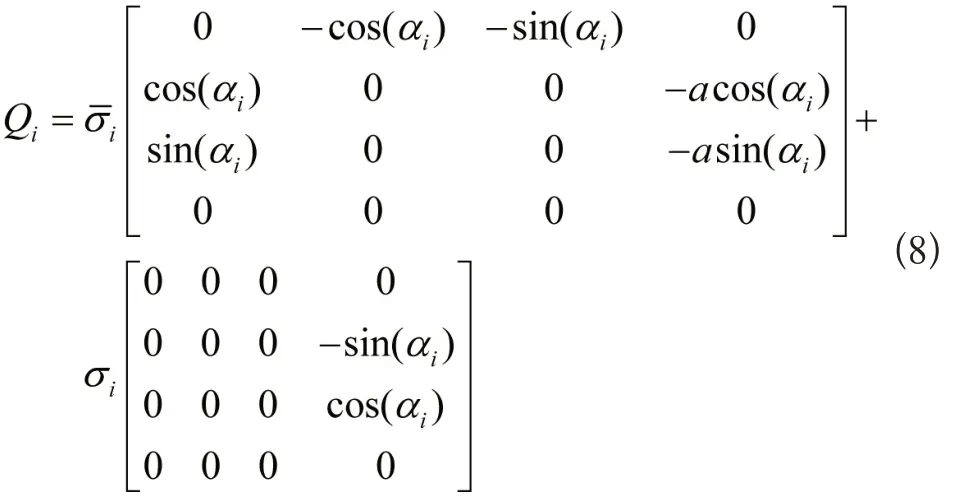
则有：

所以有：

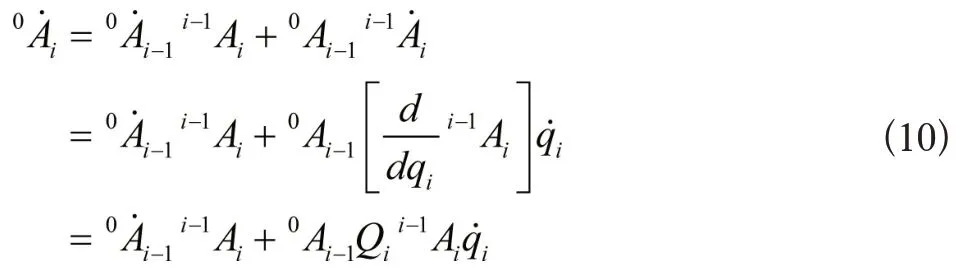
当已知机器人杆件n关节变量q时可求出其速度矩阵。

综上所述，可得改进的D-H 参数下机器人运动学问题[10-12]的计算算法框图如图2所示。

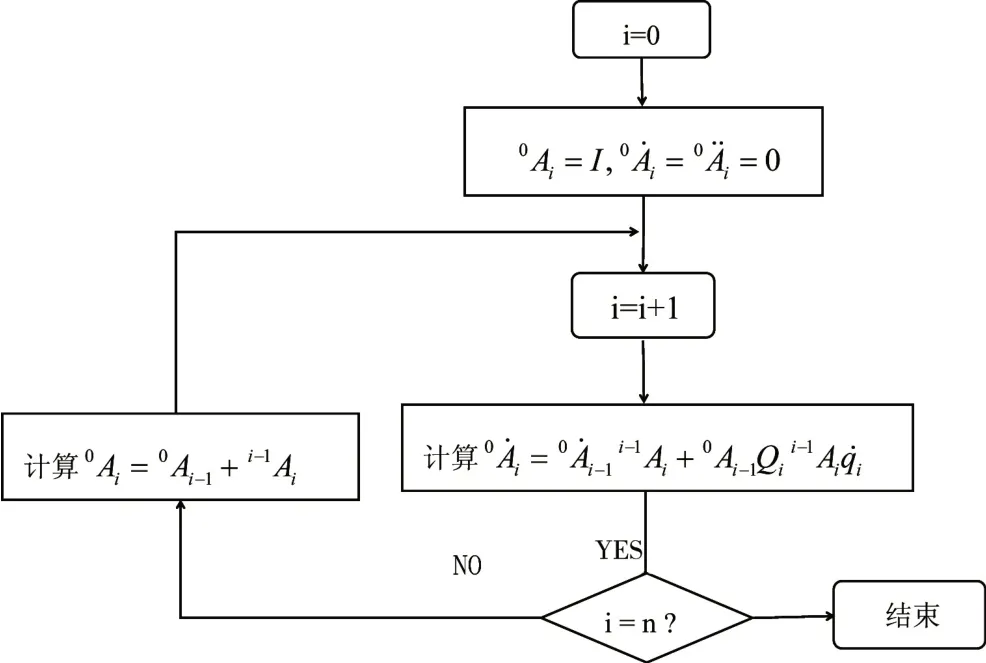
图2 改进的D-H参数下机器人运动学计算算法框图

5 计算实例

对于一般的6 自由度串联机器人，其关节类型为转动关节，此时其关节变量qi。只与改进的D-H参数的θi有关。假设某一6 自由度串联机器人改进的D-H 参数与D-H参数取值相同时，利用MATLAB 对其进行运动学仿真分析[13-14]如下：

clear tb rvcpath robotpath visionpath

% theta d a alpha offset

L1=Link([0 0 0．11 pi/2 0]，'standard')；

L2=Link([0 0 0．61 0 0]，'standard')；

L3=Link([0 0 0．12 pi/2 0]，'standard')；

L4=Link([0 0．43 0 pi/2 0]，'standard')；

L5=Link([0 0 0 pi/2 0]，'standard')；

L6=Link([0 0．12 0 0 0]，'standard')；

robot=SerialLink([L1 L2 L3 L4 L5 L6]，'name'，'DH')；figure(1)，teach(robot)；

% theta d a alpha offset

ML1=Link([0 0 0．11 pi/2 0]，'modified')；

ML2=Link([0 0 0．61 0 0]，'modified')；

ML3=Link([0 0 0．12 pi/2 0]，'modified')；

ML4=Link([0 0．43 0 pi/2 0]，'modified')；

ML5=Link([0 0 0 pi/2 0]，'modified')；

ML6=Link([pi/4 0．12 0 0 0]，'modified')；

modrobot=SerialLink([ML1 ML2 ML3 ML4 ML5 ML6]，'name'，'gaijinDH')；%连接连杆，取名机器人为gaijinDH

figure(2)，teach(modrobot)；

输出机器人的姿态位置模型如图3所示。

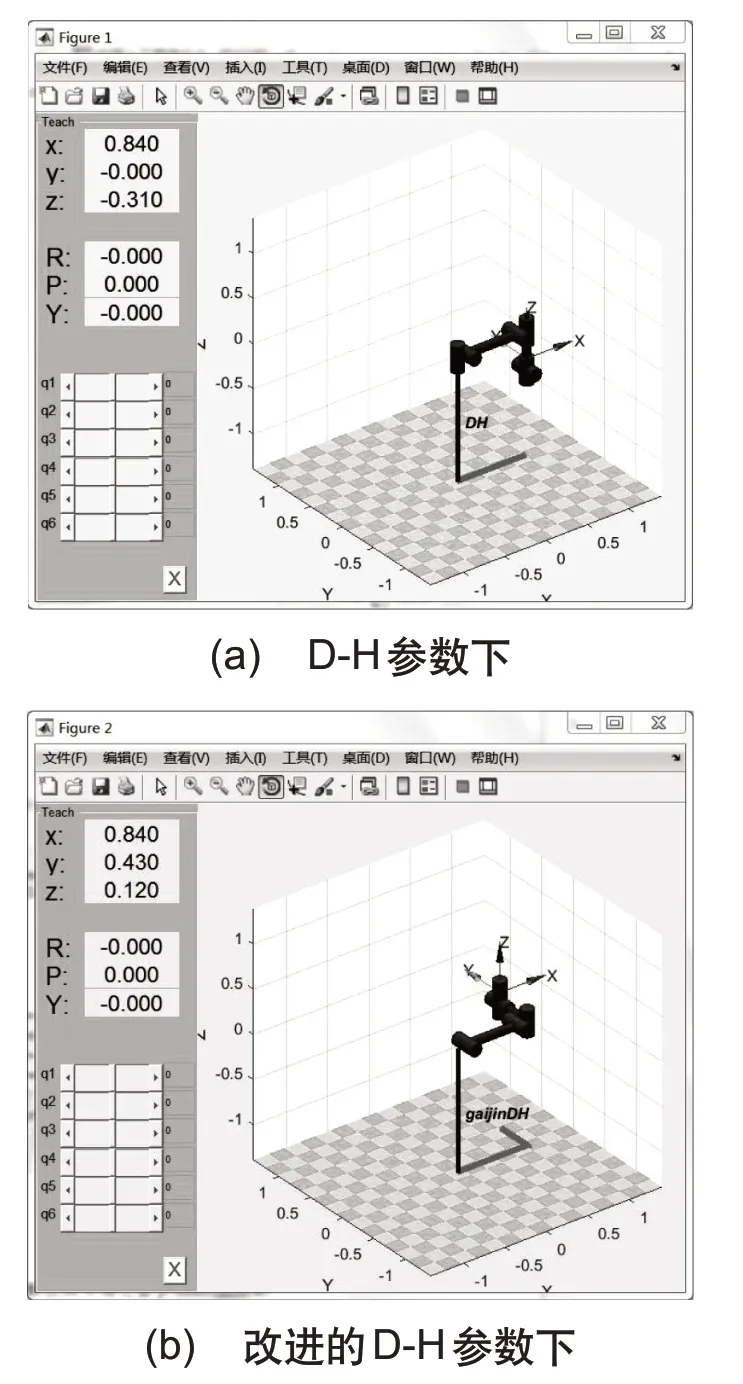
图3 6自由度串联机器人姿态位置模型图

从图3可以看出改进的D-H 参数与D-H 参数取值相同时末端位置有明显差异。

将原D-H参数乘一个变换矩阵后可得到新的改进D-H参数下模型，运行以下程序可得新的改进D-H参数下机器人输出的姿态位置模型如图4所示。

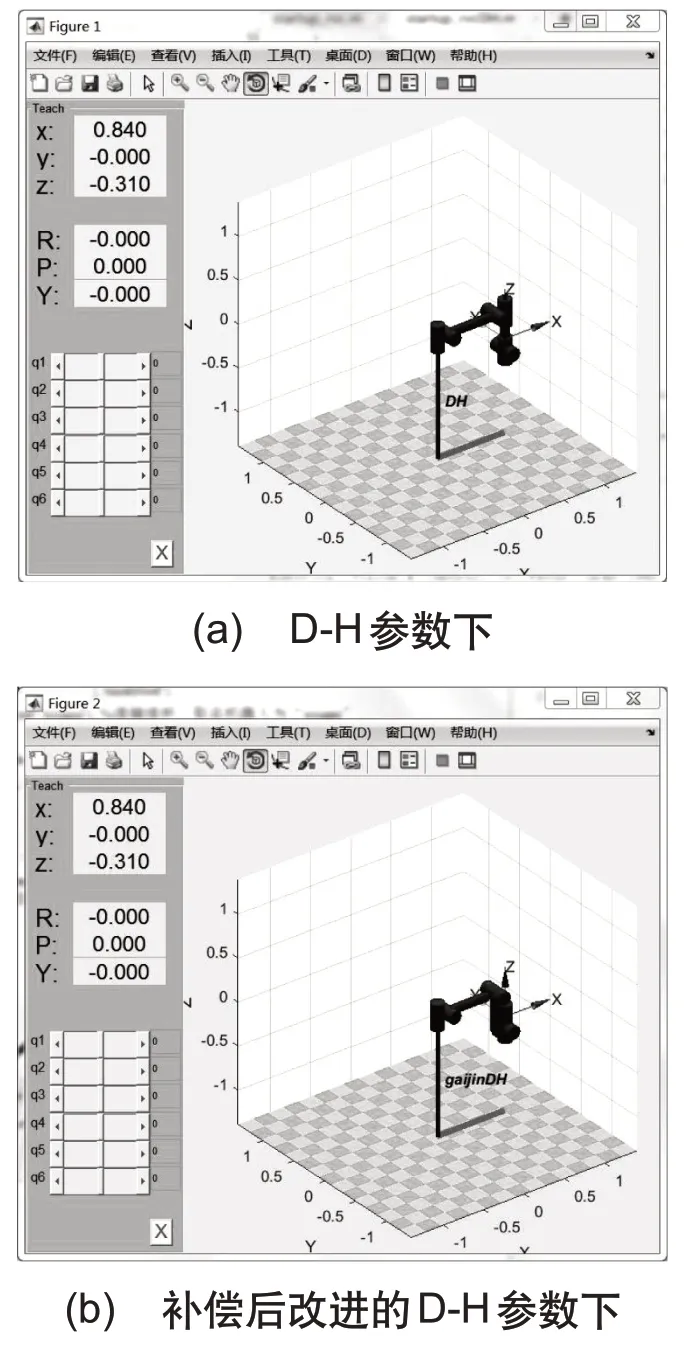
图4 6自由度串联机器人姿态位置模型图

% theta d a alpha offset

ML1=Link([0 0 0 0 0]，'modified')；

ML2=Link([0 0 0．11 pi/2 0]，'modified')；

ML3=Link([0 0 0．61 0 0]，'modified')；

ML4=Link([0 0．43 0．12 pi/2 0]，'modified')；

ML5=Link([0 0 0 pi/2 0]，'modified')；

ML6=Link([0 0．12 0 pi/2 0 ]，'modified')；

modrobot=SerialLink([ML1 ML2 ML3 ML4 ML5 ML6]，'name'，'gaijinDH')；%连接连杆，取名机器人为gaijinDH

figure(2)，teach(modrobot)；

可见对D-H 参数补偿增加了一个平移变换矩阵后，两者末端位姿输出一致。

6 结束语

应用D-H参数方法建立串联机器人杆件坐标系的Zi轴是沿杆件i的传动轴方向，而改进的D-H参数方法是选取和杆i固连坐标系的Zi轴沿杆i的驱动轴轴向。通过(6)式、(7)式可以看出，用改进的D-H 方法起对串联机器人杆件坐标系的齐次变换矩阵进行推导时，都与杆件扭角αi有着密切的关系，而传统D-H 参数推导结果则与αi无关联。当改进的D-H参数与D-H参数取值相同时，串联机器人的末端位置姿态会有明显的不同。通过图3和图4对比可以看出两种建模方法参数存在以下关系： 改进的D-H参数建模方法中四个参数{ai+1、αi+1、di+1、θi+1}与D-H参数下{ai、αi、di、θi}等价，对D-H参数乘一个变换补偿矩阵后可得到与原机器人位置姿态一致的改进的D-H参数模型。