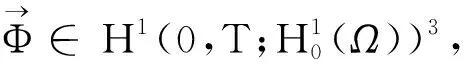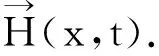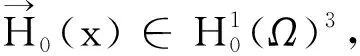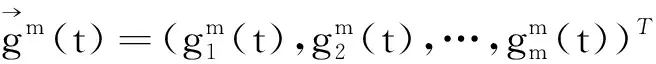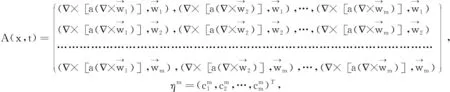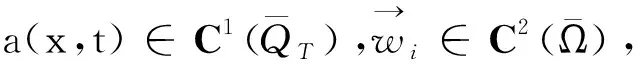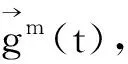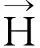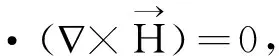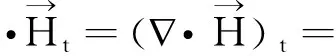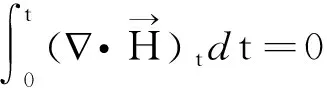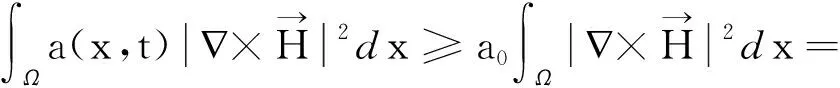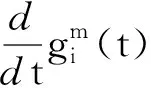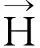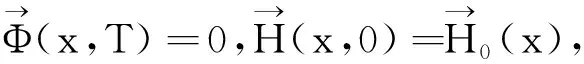一类线性抛物型方程组弱解存在性证明
旷雨阳 , 王太荣, 李兴华
(安顺学院数学与计算机科学学院, 贵州 安顺 561000)
热能的扩散以及布莱克-斯科尔斯模型等演化问题,都是以抛物型偏微分方程形式出现,抛物型偏微分方程更在流体力学、热力学、电磁学以及概率论的解析处理中都有重要应用,因此它在自然科学中有广泛应用[1-2].故而激起了许多研究者的兴趣和重视,经过研究已取得了很多成果,到目前为止,对抛物型偏微分方程解的存在性的研究成果较好,如文献[3]-[8]等.
本文采用Galerkin方法[9]讨论一类线性抛物型方程组弱解存在性证明.此类抛物型偏微分方程组在微波加热系统中应用很广,微波加热主要通过微波渗透到物体内部,微波撞击所加热物质分子,使其运动而产生热量,实现物体加热.物体内部的温度分布通过热传导实现,具体可以用Maxwell方程与热传导方程的耦合系统描述其数学模型[10].
1问题的提出
下面采用Galerkin方法讨论如下一类线性抛物型方程组及其初边值条件问题:
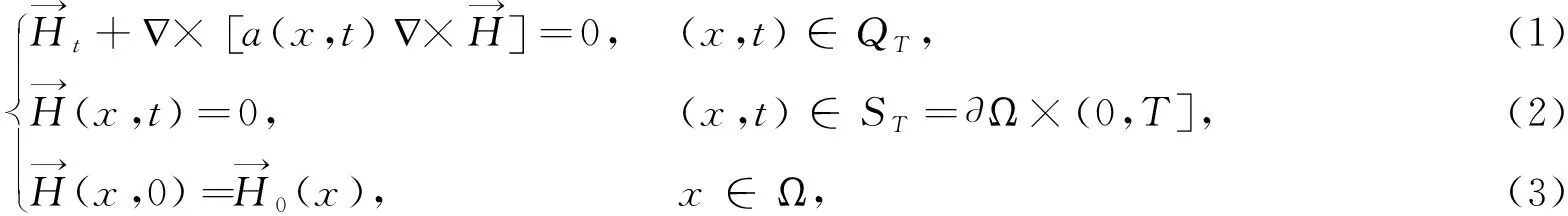
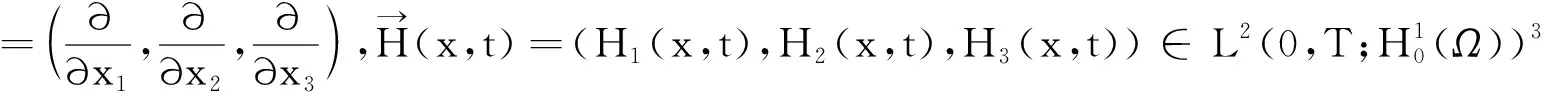
2预备知识


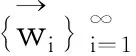
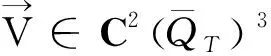
使得

命题1[9]当1 命题2[9]当1 定理2(Poincare不等式)[9]设1≤p<+∞,Ω⊂Rn为一有界区域, 定理3(紧嵌入定理)[9]设Ω⊂Rn为一有界区域,1≤p≤+∞, i) 若Ω满足一致内锥条件,则当p≤n时,下列嵌入是紧的, w1,p(Ω) w1,p(Ω)Lq(Ω), 1≤q<+∞,p=n; ii) 若∂Ω恰当光滑,则当p>n时下列嵌入是紧的, w1,p(Ω) 注1[9]上面所述的紧嵌入是指,对被嵌入空间的任何有界序列,总存在一个在嵌入空间强收敛的子序列,即嵌入算子是紧的. 定理4(存在唯一性定理)[11]设带有初值问题的常微分方程组为 如果A(t)是n×n矩阵,f(t)是n维列向量,它们都在区间a≤t≤b上连续,则对于区间a≤t≤b上的任何数t0及任一常数n维列向量η,方程组x′=A(t)x+f(t)存在唯一解φ(t),定义于整个区间a≤t≤b上,且满足初值条件φ(t0)=η. 使它满足 (4) 其中,(·,·)为L2(Ω)3中的内积,注意到 记 则有 (5) (6) 则方程组(5)与(6)转化为 即 于(0,t)上积分,进而有 (7) (8) 由Poincare不等式 (9) 对此式两端在(0,t)积分得 (10) 由(8),(9)及(10)得 由(7)式,即为 将此式整理得 所以, 其中,μ≥0为Poincare不等式中的常数,从而 (11) 于(0,T)上积分,即 进而有 将此不等式移项得 从而有, (12) 联合(11)与(12)得 (13) 其中,c是不依赖于m的常数. 在该式两端同乘以αjk,并对k从1到j求和,从而有 令j→∞,得 (14) 对此等式两边令m→∞时取极限,即得 从而有 (15) 又因为 将之代入(15)式整理得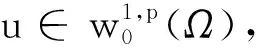

3假设条件
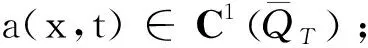
4线性抛物型方程组弱解存在性证明