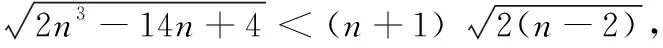几类特殊图的ABC能量
刘海琴, 邵燕灵
(1.山西农业大学基础部, 山西 太谷, 030801; 2.中北大学大数据学院, 太原 030051;3.中北大学理学院, 太原 030051)



1特殊图的ABC能量
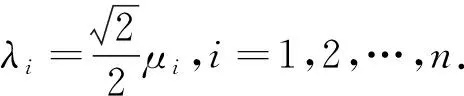
定理1当n≥3时,路图Pn的ABC能量为:
定理2当n≥3时,路图Pn的ABC特征多项式满足

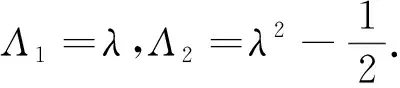
证明当n≥3时,由定义知路图Pn的ABC特征多项式为
PABC(Pn,λ)=det(λIn-ABC(Pn))=
(1)

引理2[1]如果M是非奇异矩阵,则有
定理31) 星图Sn=K1,n-1(n≥2)的ABC特征多项式为
PABC(Sn,λ)=λ2-n[λ2-(n-2)];
2) 星图Sn(n≥2)的ABC能量为
证明1) 星图K1,n-1的ABC矩阵为
(2)
因此,由引理2得到星图K1,n-1的ABC特征多项式为
PABC(Sn,λ)=det(λIn-ABCP(Sn))=
(3)

PABC(Sn,λ)=λ2-n[λ2-(n-2)].
2) 根据1) 中的结论直接计算可得
定理41) 完全图Kn(n≥2)的ABC特征多项式为
PABC(Kn,λ)=
2) 完全图Kn(n≥2)的ABC能量为
证明1) 易得完全图Kn(n≥2)的ABC矩阵为
ABC(Kn)=
(4)
于是,由引理2得到完全图Kn(n≥2)的ABC特征多项式为:
PABC(Kn,λ)=det(λIn-ABCP(Kn))=
(5)
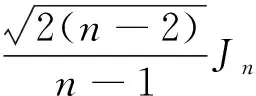
PABC(Kn,λ)=
2) 根据1) 中的结论直接计算可得
定理51) 完全二部图Km,n(m,n≠1)的ABC特征多项式为
PABC(Kn,λ)=λm+n-2[λ2-(m+n-2)];
2) 完全二部图Km,n(m,n≠1)的ABC能量为
证明1) 由于完全二部图Km,n(m,n≠1)的ABC矩阵为
(6)
于是,由引理2得到完全图Km,n(m,n≠1)的ABC特征多项式为
PABC(Km,n,λ)=det(λIn-ABCP(Km,n))=
(7)
2) 根据1) 中的结论直接计算可得
由定理5可知,完全二部图的ABC能量仅与图的顶点总数有关,而与该二部图的结构无关.
若n为任意的正整数,Fn指的是有2n+1个顶点和3n条边的友谊图.换言之,友谊图Fn是一种可以通过n个3长的圈图C3与一个公共顶点合并而形成的图.图1中给出了友谊图F2,F3和Fn.

图1 友谊图F2,F3和FnFig.1 Friendship graphs F2,F3and Fn
定理6当n≥2时,
1) 友谊图Fn的ABC特征多项式为
PABC(Fn,λ)=
2) 友谊图Fn的ABC能量为
证明1) 由于友谊图Fn的ABC特征多项式为
(8)

(9)

(10)
于是,
2) 根据1) 中的结论直接计算可得

定理7当n≥2时,

图2 风车图


(11)
令
λn+1(λ2-1)n-1(λ2-1-n).
2) 根据1) 中的结论直接计算可得
定理8对于顶点数同为m(m-1=6k,k为整数)的友谊图Fn和风车图Dn,EABC(Dn) 证明当顶点数为m(m-1=6k,k为整数)时,可知在友谊图中C3的个数为3k,在风车图中C4的个数为2k,由定理6和定理7知 易得 EABC(Dn) 本部分考虑几类特殊图在删去一条边后其ABC能量的变化. 引理2[8]令G=G1∪G2∪…∪Gp,则有 EABC(G)=EABC(G1)+EABC(G2)+ …+EABC(Gp). 定理91) 若e∈E(Pn),则有EABC(Pn-e)=EABC(Pr)+EABC(Ps),其中r+s=n; 2) 若Sn表示n个顶点的星图,且e∈E(Sn),当n≥3时有 EABC(Sn-e)=EABC(Sn-1). 定理10若e为完全图Kn(n≥4)的一条边,Kn-e为Kn(n≥4)删去一条边所得,则有 EABC(Kn-e) 证明由于图Kn-e的ABC矩阵为 由引理2得到图Kn-e的ABC特征多项式为 PABC(Kn-e,λ)=det(λIn-ABC(Kn-e))= (12) EABC(Kn-e)2特殊图删边后的ABC能量