广义BiHom-李代数与BiHom-杨-巴克斯特方程
腾 文, 游泰杰
(1.贵州财经大学数统学院, 贵阳 550025; 2.贵州师范大学数学科学学院, 贵阳 550025)
Hom-李代数是由Hartwig等[1]首次引入. 后来, 由于Hom-李代数在数学和物理中的双重应用,Larsson等[2]引入拟-Hom李代数的概念, Makhlouf和Silvestrov[3-5]先后引入Hom-代数、Hom-余代数以及Hom-Hopf代数并研究它们的一些主要性质, Caenepeel和Goyvaerts[6]用张量范畴的方法去刻画 Hom-量子群. 生云鹤[7]给出Hom-李代数的表示, 随后, 王圣祥和王栓宏[8]研究Yetter-Drinfeld 范畴中的Hom-李代数(也称为广义Hom-李代数).
BiHom-代数是一种其定义的结构恒等式被两个可交换的同态映射扭曲的代数. 这类代数是用范畴方法引入的, 它是Hom-代数的推广. 文献[9]得到BiHom-代数的基础概念、动机和结果.BiHom-代数结构包括 BiHom-结合代数和 BiHom-李代数.最近, 王圣祥和郭双建[10]给出BiHom-李超代数的量子杨-巴克斯特方程的解. 近年来, (Bi)Hom-李代数研究取得了丰富的成果, Makhlouf、Ammar、陈良云、郭双建等[11-15]借助不同的工具研究(Bi)Hom-李超(着色)代数的结构与上同调理论等内容.
作为广义Hom-李代数[8]与BiHom-李超(着色)代数[9-11,14-15]的自然推广, 本文引入广义BiHom-李代数的概念, 并给出一些例子.然后, 构造广义BiHom-李允许代数并研究广义BiHom-结合代数的性质.最后, 给出广义BiHom-李代数的杨-巴克斯特方程解.
1准备知识
本文假定k是一个特征为0的域.所有代数系统均在k上.下面简单介绍一些本文中涉及到的概念和符号, 更多有关BiHom-李代数中的概念和结果, 参见文献[9].若C为余代数, 对于余乘, 使用Sweedler[16]-型符号: Δ(c)=c1⊗c2, 对任意的c∈C.

h1m(-1)⊗h2·m0=(h1·m)(-1)h2⊗(h1·m)0,
(1)
等价于
ρ(h·m)=h1m(-1)S(h3)⊗(h2·m0),

ρ:M→H⊗M,mm(-1)⊗m0,∀m∈M.在范中, 辫子τ:M⊗N→N⊗M为
τ(m⊗n)=m(-1)·n⊗m0,


((a(-1)b)(-1)a0)⊗(a(-1)b)0=a⊗b,
等价于
a(-1)b⊗a0=b0⊗S(-1)(b(-1))a,∀a,b∈A,
则称辫子τ为对称的.

(a(-1)b)a0=ab,a,b∈A
(2)
成立, 则称A为H-交换的.
定义1[9]BiHom-结合代数是一个四元组(A,m,α,β), 其中A是线性空间,m:A⊗A→A和α,β:A→A是线性映射,满足, 对任意的a,b,c∈A,
α∘β=β∘α,α(a)(bc)=(ab)β(c).
(3)
如果α,β是代数同态, 即α(ab)=α(a)α(b)与β(ab)=β(a)β(b), 则称BiHom-结合代数A为保积的; 如果α,β是代数同构, 则称 BiHom-结合代数A是正则的.
定义2[9]BiHom-李代数是一个四元组(L,[·,·],α,β), 其中L是线性空间,α,β:L→L和[·,·]:L⊗L→L是线性映射, 满足: 对任意的a,a′,a″∈A,
α∘β=β∘α,
[β(a),α(a′)]=-[β(a′),α(a)],
[β2(a),[β(a′),α(a″)]]+[β2(a′),[β(a″),α(a)]]+
[β2(a″),[β(a),α(a′)]]=0.
如果α,β是代数同态, 即
α([a,b])=[α(a),α(b)],
β([a,b])=[β(a),β(b)],
对任意的a,b∈L,则称BiHom-李代数(L,[·,·],α,β)为保积的.特别地, 如果α,β是代数同构, 则称(L,[·,·],α,β)是正则的.
2广义BiHom-李代数

α,β:L→L, [·,·]:L⊗L→L

α∘β=β∘α,
(4)
[β(l),α(l′)]=-[l(-1)·β(l′),α(l0)],
(5)
{l⊗l′⊗l″}+{(τ⊗1)(1⊗τ)(l⊗l′⊗l″)}+
{(1⊗τ)(τ⊗1)(l⊗l′⊗l″)}=0.
(6)
对任意的l,l′,l″∈L, 其中{l⊗l′⊗l″}表示[β2(l),[β(l′),α(l″)]]和τ是L上的辫子.
如果α,β是代数同态, 即对任意的a,b∈L,
α([a,b])=[α(a),α(b)],
β([a,b])=[β(a),β(b)],
则称广义BiHom-李代数(L,[·,·],α,β)为保积的.特别地, 如果α,β是代数同构, 则称广义BiHom-李代数(L,[·,·],α,β)是正则的.
例11) 若β=α, 则广义BiHom-李代数为文献[8]中的广义Hom-李代数.
2) 若H=kG, 其中G为阿贝尔群, 则广义BiHom-李代数为文献[11]中的BiHom-李着色代数.
例2设(L,[·,·])为广义李代数,α,β:L→L为两交换的线性映射且∀a,b∈L满足:
α([a,b])=[α(a),α(b)],
β([a,b])=[β(a),β(b)],
定义[·,·]′:L→L为
[a,b]′=[α(a),β(b)],
则(L,[·,·]′,α,β)为广义BiHom-李代数.

[a,b]=ab-(a(-1)·α-1β(b))(αβ-1(a0)).
(7)
证明计算过程类似于文献[11].
类似于文献[8], 有下面例3和例4.
例3设{a1,a2}为 2-维向量空间A的基.文献[9]定义BiHom-结合代数(A,m,α,β), 乘法和线性映射α,β如下:
m(a1,a2)=a1,m(a1,a2)=ba2,
m(a2,a1)=-a2,m(a2,a2)=0,
α(a1)=a1,α(a2)=-a2,
β(a1)=-a1,β(a2)=a2,
其中b∈k.
设G为由g生成的2阶循环群, 则群代数H=kG为Hopf代数.e为群G的单位元.定义A的左-H-模作用和左-H-余模余作用为
ρ(x1)=e⊗a1,ρ(x2)=g⊗a2,
e·a1=a1,e·a2=a2,g·a1=a1,g·a2=a2,
不难验证A为广义BiHom-结合代数.
辫子τ定义为τ(a2⊗a2)=-a2⊗a2和τ(ai⊗aj)=aj⊗ai.根据定理 1, 可得广义BiHom-李代数, 其中[·,·]为:
[a1,a2]=2ba2,[a2,a1]=-a2+ba1,
[a1,a1]=[a2,a2]=0.
例4设A为3维Heisenberg李代数, 它由严格的上三角3×3复矩阵组成.具有标准的线性基

设G为由g生成的2阶循环群, 则群代数H=kG为Hopf代数.e为群G的单位元.定义A的左-H-模作用和左-H-余模余作用为
ρ(x1)=g⊗a1,ρ(x2)=g⊗a2,
ρ(x3)=e⊗a3,e·ai=ai,
g·a1=-a1,g·a2=-a2,g·a3=a3,
不难验证A为 广义BiHom-结合代数.
另一方面存在不同案例。2011年白俄罗斯国家石油公司下属子公司因同伊朗签署5亿美元合同受到美国制裁,但该制裁未追溯至其母公司[12];同年美国对以色列Ofer Brothers 集团公司的制裁仅限于其直接参与伊朗油气贸易的控股公司,也未追溯其母公司[13]。2012年7月,美国以为伊朗银行提供“重大交易协助和重大金融服务”为由,对中国石油集团旗下昆仑银行进行制裁,也未追溯至其股东中国石油集团公司[14]。
辫子τ为
τ(a1⊗a1)=-a1⊗a1,τ(a1⊗a2)=-a2⊗a1,
τ(a1⊗a3)=a3⊗a1,τ(a2⊗a1)=-a1⊗a2,
τ(a2⊗a2)=-a2⊗a2,τ(a2⊗a3)=a3⊗a2,
τ(a3⊗a1)=a1⊗a3,τ(a3⊗a2)=a2⊗a3,
τ(a3⊗a3)=a3⊗a3,
定义[·,·]为
[ai,a3]=[a3,ai]=[a1,a1]=[a2,a2]=0,
[a1,a2]=[a2,a1]=a3,i=1,2,3.
不难验证(A,[·,·])为广义李代数.
设λ1,λ2,λ′1,λ′2为k中的非零元.考虑映射α,β:L→L为
α(a1)=λ1a1,α(a2)=λ2a2,α(a3)=λ1λ2a3,
β(a1)=λ′1a1,β(a2)=λ′2a2,β(a3)=λ′1λ′2a3,
根据定理1, 可得广义BiHom-李代数(A,[·,·]′,α,β), 其中括积[·,·]为非零的,如下:
[a1,a2]′=λ1λ′2a3,[a2,a1]′=λ′1λ2a3.
3广义BiHom-李容许代数


证明对任意a,b∈L,定义李括号积[·,·]′为
[a,b]′=[a,b]-[a(-1)·α-1β(b),αβ-1(a0)].
ρ[a,b]′=ρ([a,b]-[a(-1)·(α-1β(b)),αβ-1(a0)]=
a(-1)b(-1)⊗[a0,b0]-b(-1)a(-1)⊗
[a(-1)·α-1β(b0),αβ-1(a00)],
(1⊗[·,·]′)ρ(a⊗b)=
(1⊗[·,·]′)(a(-1)b(-1)⊗a0⊗b0)=
a(-1)b(-1)⊗[a0,b0]-a(-1)b(-1)⊗[a0(-1)·
α-1β(b0),αβ-1(a00)]=a(-1)b(-1)⊗[a0,b0]-
a0(-1)b0(-1)⊗[a(-1)·α-1β(b0),αβ-1(a00)].

其次,验证李括号积[·,·]′满足等式 (7), 注意到{a⊗b⊗c}′=[β2(a),[β(b),α(c)]′]′, 计算如下,
{a⊗b⊗c}′=
[β2(a),[β(b),α(c)]′]′=[β2(a),[β(b),α(c)]-
[b(-1)·α-1(β2(c)),β-1(α2(b0))]]′=
[β2(a),[β(b),α(c)]]′-
[β2(a),[b(-1)·α-1(β2(c),β-1(α2(b0))]]′=
[β2(a),[β(b),α(c)]]-
[a(-1)·α-1β[β(b),α(c)],αβ-1(β2(a0))]-
[β2(a),[b(-1)·α-1(β2(c)),β-1(α2(b0)]+
[a(-1)·α-1β[b(-1)·α-1β(c),β-1(α2(b0))],αβ-1β2(a0)]=
[β2(a),[β(b),α(c)]]-
[a(-1)·[α-1β2(b),β(c)],αβ(a0)]-
[β2(a),[b(-1)·α-1β2(c),β-1α2(b0)]+
[a(-1)·[b(-1)·α-2β2(c),α(b0)],αβ(a0)]=
4[β2(a),[β(b),α(c)]]=4{a⊗b⊗c}.
类似的计算, 有
{(τ⊗1)(1⊗τ)(a⊗b⊗c)}′= 4{(τ⊗1)(1⊗τ)(a⊗b⊗c)},
{(1⊗τ)(τ⊗1)(a⊗b⊗c)}′= 4{(1⊗τ)(τ⊗1)(a⊗b⊗c)}.
由于(L,[·,·],α,β)为广义正则 BiHom-李代数, 有
{a⊗b⊗c}′+{(τ⊗1)(1⊗τ)(a⊗b⊗c)}′+ {(1⊗τ)(τ⊗1)(a⊗b⊗c)}′=0.
设(A,μ,α,β)为广义正则 BiHom-结合代数, 对任意a,b∈A, 定义
[a,b]=ab-(a(-1)·α-1β(b))(αβ-1(a0)).
∀a,b,c∈A,BiHom-结合子asα,β定义如下:
asα,β(a,b,c)=α(a)(bc)-(ab)β(c),
则(A,μ,α,β)为广义BiHom-结合代数当且仅当asα,β(a,b,c)=0.令
S(a,b,c)=asα,β(α-1β2(a),β(b),α(c))+ {(τ⊗1)(1⊗τ)asα,β(α-1β2(a),β(b),α(c))}+ {(1⊗τ)(τ⊗1)asα,β(α-1β2(a),β(b),α(c))}.

S(a,b,c)=[β2(a),β(b)α(c)]+ {(τ⊗1)(1⊗τ)[β2(a),β(b)α(c)]}+ {(1⊗τ)(τ⊗1)[β2(a),β(b)α(c)]}.
证明对任意的a,b,c∈A, 计算可得
[β2(a),β(b)α(c)]+
[a(-1)b(-1)·α(c),β2(a0)β(b0)]+
[a(-1)·β(b),a0(-1)·α(c)β2(a00)]=
β2(a)(β(b)α(c))-
a(-1)·α-1β(β(b)α(c))αβ-1β(a0)+
a(-1)b(-1)·α(c)(β2(a0)β(b0))-
a(-1)b(-1)c(-1)·α-1β(β2(a0)β(b0))αβ-1α(c0)+
a(-1)·β(b)a0(-1)·(α(c)β2(a00))-
a0(-1)b(-1)·α-1β(α(c)β2(a00))a(-1)·αβ-1(β(b0))=
β2(a)(β(b)α(c))-
a(-1)·α-1β(β(b)α(c))αβ-1β(a0)+
a(-1)b(-1)·α(c)(β2(a0)β(b0))-
a(-1)b(-1)c(-1)·α-1β3(a0)α-1β2(b0)α2β-1(c0)+
a(-1)·β(b)a0(-1)·(α(c)β2(a00))-
a0(-1)b(-1)·β(c)α-1β3(a00)a(-1)·α(b0)=
asα,β(α-1β2(a),β(b),α(c))+
{(τ⊗1)(1⊗τ)asα,β(α-1β2(a),β(b),α(c))}=
S(a,b,c).

S(a,b,c)=S(a(-1)c(-1)b(-1)·a00,a0(-1)·c00,
a(-1)c0(-1)·b00)
成立.
证明对任意的a,b,c∈A, 计算如下,
S(a,b,c)-S(a(-1)c(-1)b(-1)·a00,a0(-1)·c00,a(-1)c0(-1)·b00)=[β2(a),β(b)α(c)]+ {(τ⊗1)(1⊗τ)[β2(a),β(b)α(c)]}+ {(1⊗τ)(τ⊗1)[β2(a),β(b)α(c)]}-a(-1)b0(-1)c0(-1)·[β2(a0),β(b0)α(c0)]+a(-1)b0(-1)c0(-1)·{(τ⊗1)(1⊗τ)· [β2(a0),β(b0)α(c0)]}+a(-1)b0(-1)c0(-1)· {(1⊗τ)(τ⊗1)[β2(a0),β(b0)α(c0)]}= [β2(a),β(b)α(c)-b(-1)·β(c)α(b0)]}+ {(τ⊗1)(1⊗τ)[β2(a),β(b)α(c)-b(-1)·β(c)α(b0)]}+{(1⊗τ)(τ⊗1)· [β2(a),β(b)α(c)-b(-1)·β(c)α(b0)]}= [β2(a),[β(b),α(c)]]+ {(τ⊗1)(1⊗τ)[β2(a),[β(b),α(c)]]}+ {(1⊗τ)(τ⊗1)[β2(a),[β(b),α(c)]]}=0.
4广义BiHom-结合代数

a(-1)⊗y(-1)⊗a0(-1)y0(-1)⊗(a00y00)X+
a(-1)⊗y(-1)⊗a0(-1)y0(-1)⊗(a00y00)Y,
(8)
对任意的a∈X和b∈Y,其中
a0y0=(a0y0)X+(a0y0)Y∈X+Y.
证明直接验证.

a(-1)b(-1)·(xa0)(yb0)=
a(-1)·ε(y(-1))xb(a0y0)X+
x(-1)b(-1)·ε(a(-1))(ay0)Y(x0b0),
(9)
对任意的a,b∈X和x,y∈Y,其中,
a0y0=(a0y0)X+(a0y0)Y∈X+Y.
证明类似于文献[8].

证明计算过程与文献[8]类似.
例5根据例4,设{x1,x2,x3}为3维向量空间A中的基, 令X={x1}和Y={x2,x3}, 不难验证X与Y是H-交换的广义BiHom-结合代数,满足A=X+Y.则A满足等式[A,A][A,A]=0.
5BiHom--巴克斯特方程
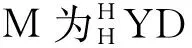
φ(α(a))∘αM=αM∘φ(a),
φ(β(a))∘βM=βM∘φ(a),
φ([β(a),b])∘βM=
φ(αβ(a))∘φ(b)-φ(a(-1)·β(b))∘φ(α(a0)).

φ:L⊗M→M,a⊗ma·m,

(α+αM)(a,m)=(α(a),αM(m)),
(β+βM)(a,m)=(β(a),βM(m)),
对任意的a∈L,m∈M.括号积 [·,·]φ定义为

对任意的a,b∈L和m,n∈M.
证明计算过程与文[14]类似.

L′=k⊕L,α(a,x)=(a,α(x)),
β(a,x)=(a,β(x)).
对任意的(a,x)∈L′.定义B:L′⊗L′→L′⊗L′为
B((a,x)⊗(b,y))=(b,β(y))⊗(a,α(x))+
(1,0)⊗(0,[x(-1)·y,x0]).
则B为BiHom-杨-巴克斯特方程的解:
(αβ⊗(β⊗α)B)∘((β⊗α)B⊗αβ)∘ (αβ⊗(β⊗α)B)=((β⊗α)B⊗αβ)∘ (αβ⊗(β⊗α)B)∘((β⊗α)B∘αβ),
对于广义BiHom-李代数(L′,α,β).
证明首先验证B与α,β是兼容的, 即,(α⊗α)∘B=B∘(α⊗α)与(β⊗β)∘B=B∘(β⊗β).令(a,x),(b,y)∈L′, 计算如下,
(α⊗α)∘B((a,x)⊗(b,y))=
(α⊗α)((b,β(y))⊗(a,α(x)) +
(1,0)⊗(0,[x(-1)·y,x0]))=
(b,αβ(y))⊗(a,α2(x))+
(1,0)⊗(0,α([x(-1)·y,x0])),
B∘(α⊗α)((a,x)⊗(b,y))=
B((a,α(x))⊗(b,α(y))) =
(b,αβ(y))⊗(a,α2(x))+
(1,0)⊗(0,α([x(-1)·y,x0])).
由此可见, (α⊗α)∘B=B∘(α⊗α).类似的可得(β⊗β)∘B=B∘(β⊗β).
其次, 验证B满足BiHom-杨-巴克斯特方程.事实上, 对任意的(a,x),(b,y),(c,z)∈L′, 一方面, 计算可得
((β⊗α)B⊗αβ)∘(αβ⊗(β⊗α)B)∘
((β⊗α)B∘αβ)((a,x)⊗(b,y)⊗(c,z))=
((β⊗α)B⊗αβ)∘
(αβ⊗(β⊗α)B)(β⊗α){(b,β(y))⊗
(a,α(x))+(1,0)⊗(0,α([x(-1)·y,x0]))}⊗
(c,αβ(z))=((β⊗α)B⊗αβ)∘
(αβ⊗(β⊗α)B){(b,β2(y))⊗(a,α2(x))⊗
(c,αβ(z))+(1,0)⊗(0,[x(-1)·α(y),α(x0)])⊗
(c,αβ(z))}=((β⊗α)B⊗αβ){(b,αβ3(y))⊗
(β⊗α)((c,αβ3(z))⊗(a,α3(x)))+
(b,β2(y))⊗(β⊗α)((0,[x(-1)·α2(z),αβ(x0)]))+
(1,0)⊗(β⊗α)((c,αβ2(z))⊗
(0,x(-1)·[α2(y),α2(x0)]))+
(1,0)⊗(β⊗α)((1,0)⊗
(0,x(-1)y0(-1)x0(-1)·[[α(x00),α(y0)],αβ(z)]))}=
((β⊗α)B⊗αβ){(b,αβ3(y))⊗(c,αβ3(z))⊗
(a,α3(x))+(b,αβ3(y))⊗(1,0)⊗
(0,x(-1)·[α3(z),α2β(x0)])+(1,0)⊗
(c,αβ3(z))⊗(0,x(-1)·[α3(y),α3(x0)])+
(1,0)⊗(1,0) ⊗(0,x(-1)y0(-1)x0(-1)·
[[α2(x00),α2(y0)],α2β(z)])=
(c,αβ5(z))⊗(b,α3β3(y))⊗(a,α5β(x))
(10)
+(1,0)⊗(0,y(-1)·[α2β3(z),α2β3(y0)])⊗
(a,α5β(x))
(11)
+(1,0)⊗(b,α3β3(y))⊗(0,x(-1)·
[α4β(z),α3β2(x0)])
(12)
+(c,αβ5(z))⊗(1,0)⊗(0,x(-1)·
[α4β(y),α3β2(x0)])
(13)
+(1,0)⊗(1,0)⊗(0,x(-1)y0(-1)x0(-1)·
[[α3(x00),α3β(y0)],α3β2(z)]).
(14)
类似的有
(αβ⊗(β⊗α)B)∘((β⊗α)B⊗αβ)∘
(αβ⊗(β⊗α)B)((a,x)⊗(b,y)⊗(c,z))=
(c,αβ5(z))⊗(b,α3β3(y))⊗(a,α5β(x))
(15)
+(c,αβ5(z))⊗(1,0)⊗(0,x(-1)·
[α4β(y),α4β(x0)])
(16)
+(1,0)⊗(b,α3β3(y))⊗(0,x(-1)·
[α4β(z),α3β2(x0)])
(17)
+(1,0)⊗(1,0)⊗(0,x(-1)x0(-1)x0(-1)·
[[α3β(x000),α2β2(z)],α4β(y)])
(18)
+(1,0)⊗(1,0)⊗(0,x(-1)y0(-1)x0(-1)·
[α4β(x00),[α3β(y0),α3β(z)]])
(19)
+(1,0)⊗(0,y(-1)·[α2β3(z),α2β3(y0)])⊗
(a,α5β(x)).
(20)
显然, (10)=(15), (11)=(20), (12)=(17), (13)=(16).因此, 如果该等式 (14)=(18)+(19)成立, 则以上两项是相等的, 即
(1,0)⊗(1,0)⊗(0,x(-1)y0(-1)x0(-1)·
[[α3β(x00),α3β(y0)],α3β2(z)])=
(1,0)⊗(1,0)⊗(0,x(-1)x0(-1)·
[[α3β(y),α2β2(z)],α4β(x00)])
+(1,0)⊗(1,0)⊗(0,x(-1)y0(-1)x0(-1)·
[α4β(x00),[α3β(y0),α3β(z)]]).
只需验证下列等式,
y(-1)·[[α3β(x),α2β2(z)],α4β(y0)]+
[α4β(x),[α3β(y),α3β(z)]]=
[[α3β(x),α3β(y)],α3β2(z)]
利用L的斜对称性, 有
[[α3β(x),α3β(y)],α3β2(z)]=
-y(-1)x(-1)·[α2β3(z),[α4(x0),α4(y0)]]
与
[[α3β(x),α2β2(z)],α4β(y)]=
-x(-1)y0(-1)·[α3β2(z),[α4(y0),α3β(x0)]]=
x(-1)y0(-1)x0(-1)·[α3β2(y0),[α2β2(z),α5β-1(x00)]].
则有

其中,
x*=α4β-1(x),y*=α3(y),z*=α2β(z).
推论1符号如定理3, 则B是可逆的, 其逆如下:
B-1((a,x)⊗(b,y))=(b,α-1(y))⊗ (a,β-1(x))+(0,[α-2(x),α-1β-1(y)])⊗(1,0),
对任意的(a,x),(b,y)∈L′.进一步,B-1是广义 BiHom-李代数(L′,α,β)的BiHom-杨-巴克斯特方程解.
证明首先验证B∘B-1=idL′⊗L′.事实上, 对任意的(a,x),(b,y)∈L′, 有
(B∘B-1)((a,x)⊗(b,y))=
B((b,α-1(y))⊗(a,β-1(x))+
B((0,[α-2(x),α-1β-1(y)])⊗(1,0))=
(a,x)⊗(b,y)+(1,0)⊗
(0,x(-1)·[α-1(y),β-1(x0)])+
(1,0)⊗(0,[α-1(x),β-1(y)])+(1,0)⊗
(0,(x(-1)+y(-1))·[[α-2(y0),α-1β-1(x0)],0)=
(a,x)⊗(b,y)+
(1,0)⊗(0,x(-1)·[α-1(y),β-1(x0)])+
(1,0)⊗(0,-x(-1)·[α-1(y),β-1(x0)])=
(a,x)⊗(b,y).
因此B∘B-1=idL′⊗L′.类似地, 可验证B-1∘B=idL′⊗L′.所以B-1是B的逆.此外, 不难验证B-1是广义 BiHom-李代数的BiHom-杨-巴克斯特方程解.
致谢感谢郭双建教授对本文提出的宝贵意见.

