围绕知识“生成” 提高课堂实效——以《等差数列的前n项和》为例

顾维维

围绕知识“生成”提高课堂实效——以《等差数列的前项和》为例

顾维维

（江苏省苏州市吴中区木渎金山高级中学，江苏苏州215128）

课堂教学是学生知识生成、思想锻炼、技能习得的主阵地，围绕知识“生成”，关注过程性教学，让学生“亲”经历“真”思考，参与其中又“乐”在其中，提高课堂教学实效。

等差数列；首尾配对

高效课堂教学的一个重要特点是在教与学的过程中让知识真实、自然地生成，对关键问题的细节设计往往是“成败”的关键。笔者通过听课学习有感而发，结合自身教学实践，以《等差数列前n项和》为载体，阐述教学应如何围绕知识生成而设计，进而从根本上提高课堂实效。

一、问题的提出

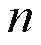
二、教学问题诊断与策略

如何让“倒序相加”的思想在学生脑海里自然生成？首先高斯算法需要“配对”，当项数不定时，就要讨论项数的奇偶性，讨论起来就比较烦琐，是否有简便的算法成为客观需求，这是需求铺垫。其次，通过问题情境建立数学模型，设置问题1和问题2及其变式，让学生深刻理解高斯算法的关键就是“配对”以及具体如何配对。这是知识与技能铺垫。最后借助问题情境中“三角形数”模型的几何直观，同时结合“数的首尾配对”，学生容易想到“形的首尾配对”，即图形的“倒置、拼补”思想萌芽就自然形成了，从“数”与“形”两个角度突破难点。

三、教学过程

（一）创设情境，提出问题

传说古希腊毕达哥拉斯学派的数学家经常在沙滩研究数学问题，他们在沙滩上画点或用小石子表示数。一定数目的点或圆在等距离的排列下可以形成一个等边三角形，这样的数被称为“三角形数”，如下图所示。

那么第100堆的石子数是多少？

教师：这个题目蕴含了哪些我们前面学过的知识？请同学们回忆一下。

教师：第100堆的石子数是多少呢？

学生：第100堆有100层，若记最上面一层为第1层，那么第1层1个，第2层2个，第3层3个……第100层是100个，所以第100堆的石子数是1+2+3+4+……+98+99+100=？

教师：观察这组数的求和有什么特点？

学生：这是一个首项和公差都是1的等差数列的前100项之和。

设计意图：第一，对于“三角形数”模型，学生在前面学习数列的通项公式时已学习，使得学生能够快速抓住关键问题，引出本节所要解决的问题。同时结合教师引导，学生能够内化前面学的等差数列的相关概念。第二，“三角形数”模型是本节课的主要载体，贯穿于整个课堂教学活动。第三，模型本身拉近了与学生之间的距离，营造了轻松的学习氛围，体现了情境引入的人文价值和应用价值。

（二）探索质询，追根溯源

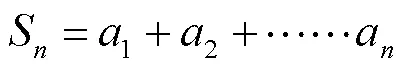
情境中的所求问题可以表示为：

教师：怎样快速求出其和？

学生：考虑“首尾配对”，1+100=2+99=3+98=……=50+51。

教师：漂亮！你的想法很有创意，计算起来非常简便。

巧合的是，德国著名数学高斯在他10岁的时候就解决了这样一个问题，和这位同学想法一致，通过对应首尾配对，将不同数的求和问题转化为相同数的求和问题，即100=1＋2＋3＋……＋100＝（1＋100）＋（2＋99）＋……＋（50+51）＝101×50＝5050.

教师：这种解法非常好，但是有没有什么弊端？

学生：不是都能配对的，比如项的个数是奇数个。

教师：很好！请同学们看问题2。

问题2：计算99=1+2+……+99的值。

教师：此时又如何解决呢？

学生1：99＝（1+2+……+99+100）－100=100－100＝4950。

教师：厉害！通过加一项减一项实现部分配对，化奇为偶，从而找到“相同数”，有没有其他解法了呢？

学生2：99=（1＋2＋……＋98）＋99＝98＋99＝99×49＋99＝4950。

学生3：99=1＋（2＋……＋99）＝1＋101×49＝4950。

学生4：99＝（0+99）＋（1＋98）＋……＋（49＋50）＝99×50＝4950。

设计意图：首先给出一个连续偶数项和的求和，理解首尾配对求和的原理和方法，然后通过问题2引导学生对连续奇数项和的求解问题的思考，进而更深层次地理解高斯求和的精髓和局限性，为后面倒序相加法的使用做出铺垫。

问题3：以上我们仅仅是从数的角度构造“首尾配对”进行研究，请同学们回到问题情境中去，能否从其他角度考虑问题1呢？（小组合作讨论）

小组代表：对图形也进行“首尾配对”。

教师：你能画出草图吗？

学生展示。

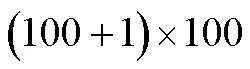
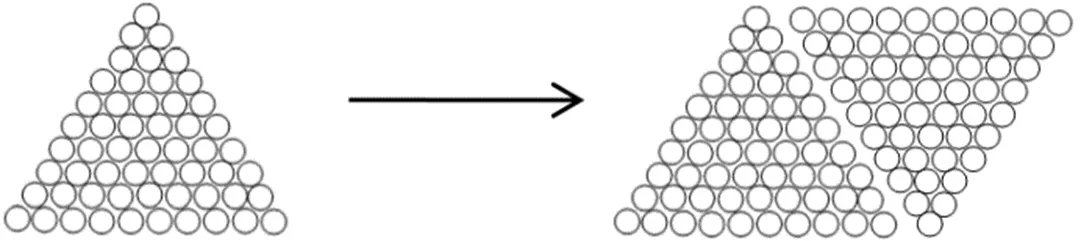
设计意图：高斯算法需要“配对”，当项数不定时，那么就要讨论项数的奇偶性。为了改进算法的同时引出倒序相加原理就设置了问题3，前面研究的“首尾配对”求和是从数的角度，借助情境中的几何模型求和的。此时学生容易想到从“形”的角度考虑“图形首尾配对”，即图形的“倒置、拼补”思想萌芽就自然形成了。紧接着，学生经过小组合作探究，动手试验，画出草图，得出结果。

问题4：如果将问题1中的100改为n，请计算S=1＋2＋3＋……＋.

教师：比一比谁算得既快又准。

教师：很好，那么对上述解法，如何用数学语言表示出来？

两式相加，得2S＝（＋1）＋（＋1）+……+（+1）＝（+1）

教师：这种算法妙在哪里？你能给它起个名字吗？

学生：不用考虑项数的奇偶问题，“首尾配对相加法。”

教师：很好，抓住了本质！

上述解法可以总结为两步：首先倒序表示出S，然后两式相加，所以在数学上称这种解法为倒序相加法。

设计意图：①根据问题3的讨论，学生容易想到通过倒置配对，拼补成平行四边形解决，强化学生对倒序相加法理解和运用；②避开了对项数奇偶的讨论，使得教学活动更加紧凑连贯，学习目标更加清晰明确；③引导学生由图形语言——数学语言——符号语言的转化，培养学生的数学抽象和逻辑推理的数学素养。

教师：前面我们研究了100，S，都是从1开始加起来，能从其他数开始吗？

问题5：根据问题情境，从第4行到第n行共有多少个石子？（小组合作探究并画出草图）

教师：都很棒，前面同学利用问题4的方法，将“梯形倒置”转化为平行四边形处理，后面同学使用“分割”手段，整体减去部分，在问题1结论的基础上计算，两种解法答案化简后是一致的，可谓“殊途同归”！（几何画板动态展示，如下图所示）

设计意图：由三角形倒置拼补，类比研究梯形倒置拼补，进一步强化学生对倒序相加法原理的理解和运用，为后面等差数列求和公式的推导奠定了基础。

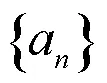
（三）自主探究，汇报交流

S＝1＋2＋3＋……＋a-2＋a-1＋a

S＝a＋a-1＋a-2＋……＋3＋2＋1

两式相加得，2S=（1＋a）＋（2＋a－1）＋……＋（a＋1）=（a＋1）

S＝1＋2＋3＋……＋a=1＋（1＋）＋（1＋2）＋……＋[1＋（－1）]

S＝a＋a－1＋……＋1=a＋（a－）＋（a－2）＋……＋[a－（－1）]

两式相加得2S＝（1＋a）＋（1＋a）＋（1＋a）＋……＋（1＋a）＝（1＋a）

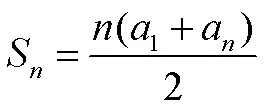
S＝1＋（1＋d）＋（1＋2d）＋……[1＋（－1）]

＝1＋[1＋2＋……（－1）]

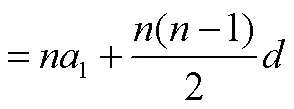
教师：（1）公式一和公式二是否相等？请给出严格证明；

（2）这两个公式中共包含哪些量？如何选取合适公式进行计算？

设计意图：从问题3到问题5，让学生经历特殊——一般——再一般的探究过程。基于上述活动经验的积累，学生对问题6等差数列求和公式的推导变得水到渠成。在这个过程中放手让学生自主推导，并交流成果，使学生对倒序相加法认识得到了进一步的升华。

四、反思与感悟

（一）以教材为方向，用“好”教材，精心设计问题情境

笔者参阅了各个版本的教材，深刻挖掘教材中所给情境的内涵，以及它们之间的区别和联系，认为问题情境的创设应“源于课本，高于课本”，一般应遵循适用性、目的性、科学性和趣味性原则。本文创设的问题情境是从学生熟悉的“三角形数”入手，引出“高斯算法”，让学生理解其“配对”思想，为后面问题1和问题2的研究做了较好知识准备；同时借助“三角形数”模型的几何直观，为后面问题4、5、6的研究做了思想、方法准备，贯穿于整个教学活动之中。

（二）以问题为主线，遵循知识生成、发展规律

教学活动的设计是基于“人”为前提，设计是“为人服务”的，应遵循知识生成方式和发展的规律。尤其在重难点处的设计应充分以学生为中心，站在学生的角度看待问题，想学生之所想，解学生之所惑。如何让“倒序相加”的思想在学生脑海里自然生成？这就是本节课的难点，教学设计以问题串线贯穿始终，从问题情境到问题1，从问题1到问题6，始终秉持以自主探究、动手实验、合作交流、成果展示、“查缺补漏”的方式让学生参与进来，问题设置上层层递进，分散问题难度，将重难点逐步“瓦解”。

（三）以重视“过程性教学”为原则，建构高效教学活动

《普通高中数学课程标准（2017年版）》明确提出学习评价既要关注学习结果，更要重视学生学习过程。过程性教学的关键是要创造合适的条件将学生“融入”到教学活动上来，让学“亲经历，真思考”。比如在前面问题探讨时，学生会遇到不定项数连续等差数列求和时该怎么办，是硬着头皮分类讨论算下去，还是“另寻出路”？教师应留有一定时间让学生经历这样一个思维过程，而不是直接或间接说出结果，再或者“逼着”学生往这个结果上引导。本文适时给出了问题3，让学生主动发现可以从“数”和“形”两个角度同时考虑，此时的学生有了一种“恍然大悟”。有了这种思想萌芽，紧接着让学生思考、试验，然后交流成果。让学生真实经历了这样一个自主探究的完整过程，从根本上提高了课堂教学的有效性。

[1] 中华人民共和国教育部.普通高中数学课程标准(2017年版)[M].北京:人民教育出版社,2018.

G632

A

1002-7661(2022)10-0135-03