舰船水润滑轴承等效支点预测及轴系迭代校中

闫琦隆， 欧阳武， 刘祺霖

(1.武汉理工大学 船海与能源动力工程学院，湖北 武汉 430063； 2.武汉理工大学 交通与物流工程学院, 湖北 武汉 430063； 3.国家水运安全工程技术研究中心 可靠性工程研究所，湖北 武汉 430063)

艉轴承是舰船推进轴系的重要组成部分，在轴系校中和动力分析中通常需要将轴承简化为等效支撑点(指距轴承后端面的距离)[1-2]。舰船尾轴承等效支点一般参照相关标准和规定选取，其中，国内的推进轴系校中计算主要是参照标准CB/Z 338-2005和《钢质海船入级规范》。根据标准CB/Z 338-2005，对于白合金轴承衬、铁梨木轴承衬和橡胶轴承衬，尾管后轴承的等效支点取值范围分别为(1/7～1/3)L、(1/4～1/3)L和(1/3～1/2)L，L为轴承长度；推进轴系其他径向轴承的等效支点均取1/2L[3-4]。有限元建模研究方法在船舶及轴承应用广泛[5]，刘亮[6]基于此方法对后尾轴承支点位置进行研究并计算得到的轴承支点位置在(1/4～1/3)L之间。等效支点的取值对舰船推进轴系动力性能预测有较大影响。刘正林等[7]分析了船舶尾轴末端在螺旋桨集中载荷作用下的挠曲特性，研究结果表明尾轴倾角的增大使得轴承末端液膜压力急聚增加，轴承边缘效应明显。在螺旋桨悬臂作用下，舰船推进轴系挠曲变形明显，等效支点在轴承中间的假设误差较大[8-9]。

尾轴弯曲程度、尾轴承结构和材料均会影响其等效支点的取值。余华军[10]利用多点支承模型，通过数值计算确定赛龙尾管轴承的等效支点位置，仿真发现随着尾管轴承刚度的增加，尾管后轴承的等效支点向后移动，而尾管前轴承的等效支点向前移动。现有的标准多根据前期应用最多的丁腈橡胶尾轴承建立，该轴承弹性模量小(约6 MPa)，轴承很长(长径比达4∶1)[11-13]。随着材料科学和轴承设计理论的发展，尾轴承材料和结构正在发生显著变化。例如，目前国内外舰船大量采用的赛龙和飞龙材料弹性模量约300～500 MPa，英国ACM公司L2、英国Trelleborg公司Orkot和荷兰wärtsilä公司的高分子复合材料弹性模量约2 300～3 000 MPa。这些变化使尾轴承承载能力有了显著提升，随着当代舰船吨位的提升，螺旋桨作为推进器[14]其重量不断增大，尾轴悬臂挠曲状态也在改变。这些因素导致舰船尾轴承等效支点位置随之变化[15-17]。

现有的尾轴承等效支点相关标准主要存在不足：1)取值范围不够准确，且有待更新；2)研究人员主要根据经验取值，缺乏对具体尾轴承结构和轴系弯曲状态的准确考虑。为此，本文首先给出基于有限元的舰船尾轴承等效支点计算方法，然后通过数值计算得到不同轴线倾角、长径比和弹性模量的等效支撑点位置数据集，最后建立尾轴承等效支点计算式，为舰船水润滑尾轴承设计提供较准确的计算方法。

1 尾轴承接触模型建立及仿真

一般可以采用接触理论或流体动压润滑理论来计算尾轴承等效支点位置[18]，2种都是根据压力分布(水膜压力分布或接触应力分布)计算力矩平衡时的等效支点。鉴于服役状态的舰船水润滑后尾轴承常处于混合润滑状态，且具有时变性，本文采用不考虑水膜的纯接触模型进行研究。其中，有限元法在尾轴承接触模型计算和轴系校中有着广泛的应用[19-21]。

1.1 尾轴承等效支点位置计算方法

舰船尾轴与尾轴承之间形成圆柱体与圆柱内孔之间接触。接触时，一方面由于垂向挤压会在垂向方向产生垂向接触力，另一方面由于切向方向的相对滑动会产生切向摩擦力。接触过程中接触状态会随着时间不断变化，为此，需要注意接触问题的方程应写成增量迭代形式，并在求解方程中引入接触定解条件。

接触区边界有关单元的控制方程可通过虚功原理给出，虚功原理指出：外力在虚位移中所做虚功等于内力在相应虚变形上所做虚功。外力和内力虚功如下：

(1)

(2)

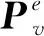
基于虚功原理的外力虚功与内力虚功相等，且接触问题边界条件不断改变，将该表达式改写成增量形式，即在时间t+Δt位形内与平衡条件相等效的有限元控制方程为：

(3)

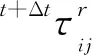
根据有限元法求解尾轴承接触模型，得到接触应力分布，然后根据力矩平衡求解尾轴承等效支点位置。首先将尾轴承沿着轴向等分为若干单元，然后将每个单元Zi中所有节点的支反力FYij累加得到该单元的总支反力FYi，最后根据力矩平衡原理，计算尾轴承的等效支点位置Zc：

(4)

式中Zc和Zi分别表示等效支点和单元中点距轴承后端面的距离。

如图1等效支点示意图所示，O为轴承几何中点，O1为等效支点的位置。轴承在实际工作时易受到如两端受力不均等因素的影响导致轴线倾斜，从而使等效支点的位置与轴承的几何中点位置不重合。本文对等效支点的定义采用无量纲形式，即等效支点离轴承后端面距离与轴承长度的比值Zc/L。

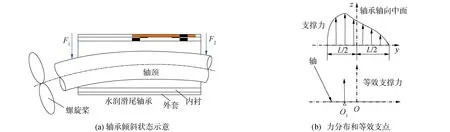
图1 等效支点示意

1.2 研究对象及有限元计算流程

关于尾轴承接触压力分布仿真，首先建立尾轴承的三维模型，然后利用有限元软件建立尾轴承接触模型(如图2所示)，仿真计算得到轴承内衬接触压力分布。

图2 基于有限元的尾轴承接触模型

由于几种水润滑尾轴承内衬材料的泊松比相差不大，且仿真发现泊松比对轴承等效支点位置影响较小，因此本文重点研究轴线倾角、轴承的长径比和轴承内衬材料的弹性模量对尾轴承等效支点位置的影响。采用控制变量法，保证其他因素不变的情况下改变其中一个因素逐一研究。几种尾轴承内衬材料如表1所示。

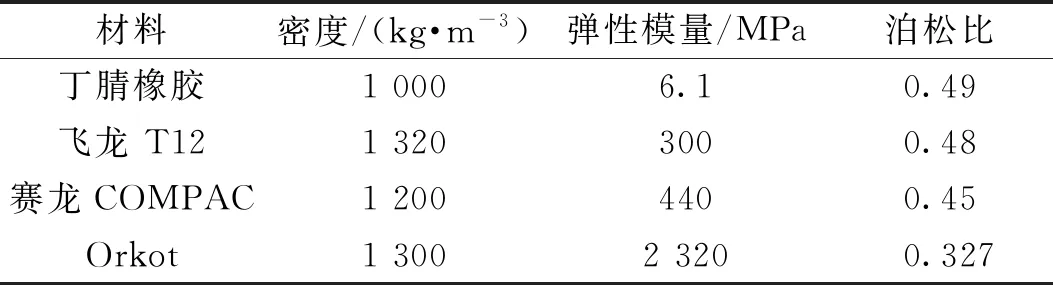
表1 几种尾轴承内衬材料的物性参数

通过在尾轴承两端轴上施加不同的载荷来模拟轴倾斜状态，改变两端载荷的大小来得到不同的倾角，从而得到不同倾角下的尾轴承接触压力分布，不同倾角下轴承总载荷不变，为10 kN，载荷F1和F2距各自轴承端面的距离为D1和D2，如式(5)所示：

(5)

式中：D1和D2为力作用点距端面距离，mm；L/D为长径比。

尾轴承的直径为350 mm，尾轴承的长径比取值范围为在2～4；尾轴承内衬材料的弹性模量取值包括：7、400、1 000、1 600、2 300 MPa。

2 尾轴承载荷分布和等效支点的影响因素分析

轴承主要设计参数包括：直径、长径比、间隙、内衬弹性模量和泊松比，研究表明，长径比和内衬弹性模量对轴承载荷分布以及应变分布影响较大，而其他因素影响较小，因此本文选择这2个参数为主要变量。轴承内衬弹性模量为1 000 MPa，轴承两端分别施加6 kN和4 kN的力时，得到不同长径比下轴承内部的应变分布曲线，如图3所示。

首先分析长径比对轴承应变分布和等效支点位置的影响。从图3可以看出，在内衬弹性模量和施加载荷一致的情况下，随着长径比增大，轴承内部应变值逐渐减小，长径比为4.0的尾轴承内部应变值相比长径比2.0的数据减小了约98%，且应变分布更加均匀，应变的变化范围也更加小。综合图4可得，在倾角和弹性模量不变时，尾轴承长径比对等效支点位置的影响较为复杂，并非简单的正相关或者负相关关系。当长径比处于2.5～4的区间内，随着长径比的增大，等效支点位置的无量纲坐标呈减小的趋势，且各弹性模量下变化趋势具有一致性；当长径比小于2.5时，不再服从此变化趋势。

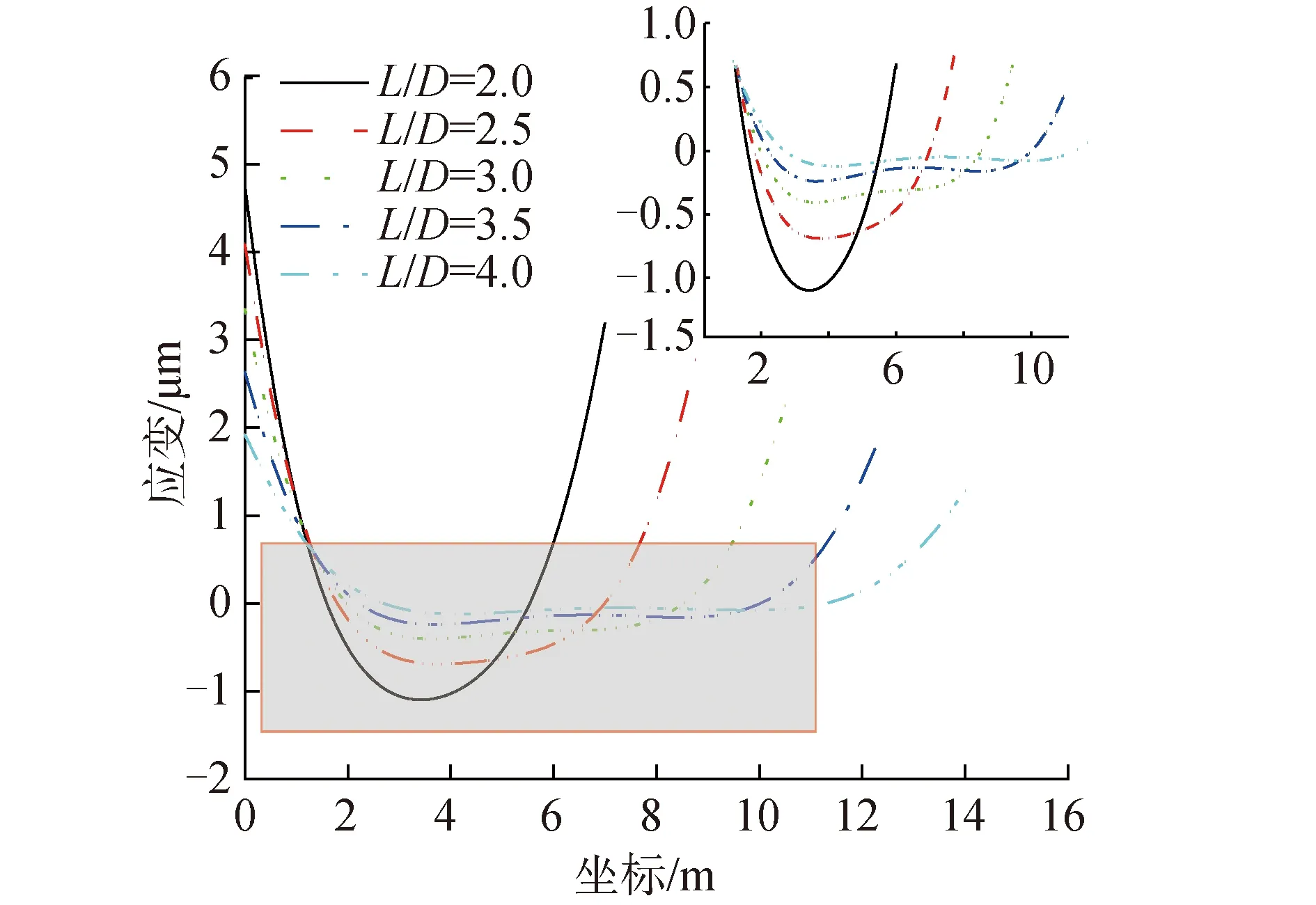
图3 弹性模量为1 000 MPa时轴承应变分布

此外，在尾轴承内衬弹性模量一致时，各个长径比下的尾轴承等效支点位置随倾角的变化趋势一致。例如在长径比为2.5，弹性模量为1 000 MPa时，随着轴线倾角的增大，尾轴承等效支点位置值呈线性减小。

进一步改变水润滑尾轴承内衬弹性模量的轴承等效支点位置仿真结果如图4所示，可以看出，当轴承长径比和轴线倾角不变时，轴承等效支点的值随其内衬弹性模量的增大而减小，即等效支点的位置距离轴承中点越来越远，距离轴承端面越来越近，结合有限元模型可知，尾轴承等效支点位置靠近受力较大的轴承端面一侧。而且，3个因素对尾轴承等效支点位置的耦合影响较弱，几乎相互独立。

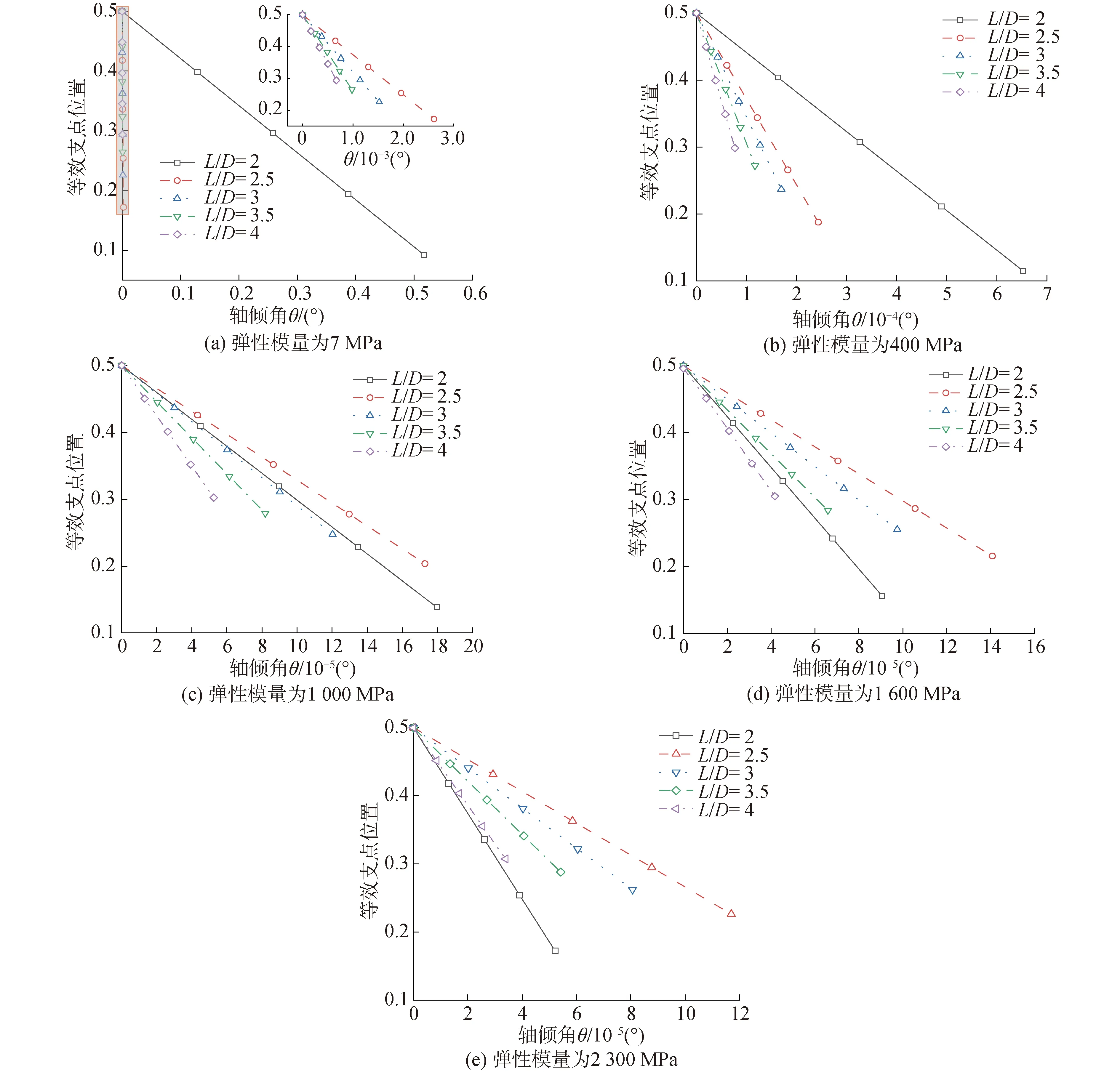
图4 不同长径比及弹性模量下等效支点位置随倾角的变化曲线

3 尾轴承等效支点位置计算式

3.1 等效支点位置计算式拟合

根据上述仿真结果，针对线性材料的水润滑尾轴承等效支点位置与3个因素的关系可用函数式表示为：

Z=f(θ,E,L/D)

(6)

由于这3个影响因素之间几乎相互独立，可以分别拟合后进行组合。长径比取2～4、弹性模量取7～2 300 MPa以及不同轴线倾角可组合共形成125组轴承方案，对这些方案对应的尾轴承等效支点位置数据进行曲线拟合，可得到水润滑尾轴承无量纲等效支点位置计算式如下：

Z=f(θ,E,L/D)=[g1(L/D)+g2(L/D)×

Eg3(L/D)]×θ+0.5 2.5≤L/D≤4

(7)

其中：

(8)

对125组数据进行反算验证，当长径比不小于2.5时，轴承等效支点位置拟合公式解与有限元仿真解的相对误差平均值约1%，最大值为6%(只有一个)，表明该拟合方法具有很高精度。

3.2 计算式的应用验证

重新设计7种算例，对应的轴承参数如表2所示，分别利用上述拟合计算式和有限元法计算轴承等效支点位置，开展式(7)、(8)的应用验证。可知，当水润滑尾轴承长径比为950/350，轴承内衬弹性模量为400 MPa，轴倾角为2.189×10-4(°)时，代入式(7)可得轴承等效支点位置为0.204 9，与有限元仿真解的相对误差为1.8%。其他6个算例的计算误差均小于4%，再次验证了本文给出的尾轴承等效支点拟合计算式具有较高的计算精度。

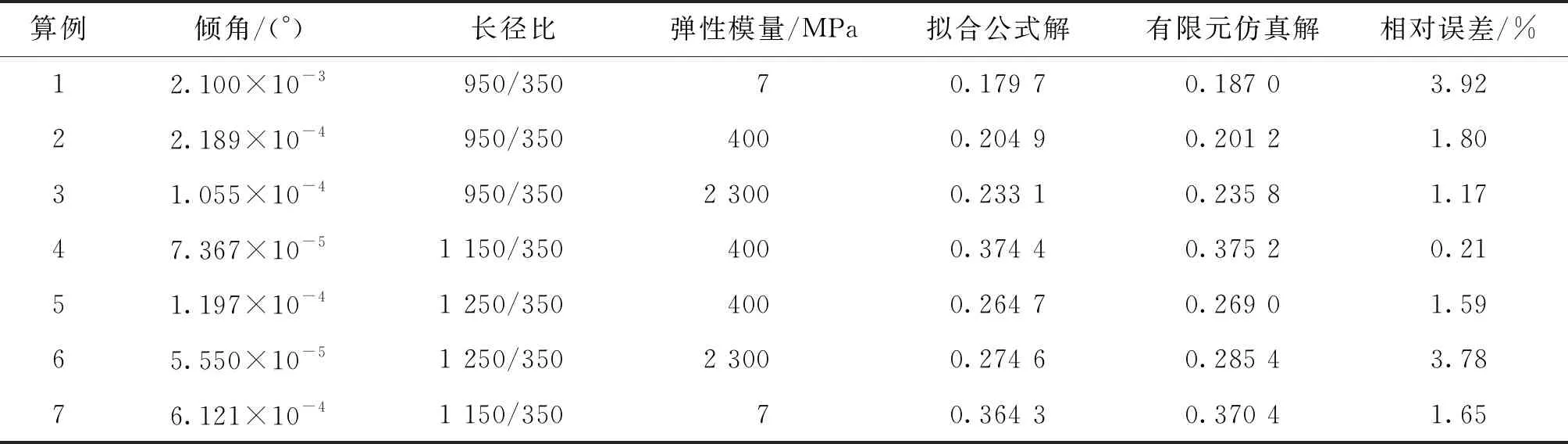
表2 尾轴承算例的参数和计算结果

4 融合轴承支点位置预测的推进轴系校中迭代计算方法

三弯矩法是用解平面力系静不定问题的方法，它将轴系视为放置在各个刚性铰支座上的连续梁，而在梁的各截面变化处和集中力作用点都假定有一个虚支座。传统的三弯矩法假设尾轴承等效支点为固定值，比如1/3或1/4。迭代计算方法的核心在于尾轴承等效支点位置根据轴倾斜状态不断迭代调整，这与实际轴系状态更相符。校中迭代计算方法的基本步骤为：给出尾轴承等效支点的初始值Z(0)，例如1/3，利用三弯矩法进行轴系校中计算，获得尾轴承处的轴线转角；利用尾轴承等效支点计算式，将轴线转角带入，计算得到新的等效支点位置Z(k)，k为迭代次数；对比前后2次迭代计算中的等效支点位置，当两值相差较大时，需修正等效支点位置后重新上2步的操作；当2值足够接近时，认为此时的等效支点位置正确，然后代入三弯矩法计算得到最终的校中计算结果，迭代收敛的判据如式(9)所示，b为迭代收敛系数，本文取0.001：

(9)

推进轴系校中迭代计算方法的流程图如图6所示。可以看出，该方法的本质在于解决尾轴承轴线弯曲状态与尾轴承等效支点位置关系的自恰，避免主观假设的尾轴承支点位置与实际服役轴系状态不符的问题。

通过将本文等效支点位置计算式应用于推进轴系校中迭代计算法的结果与基于有限元校中算法的结果进行对比，验证本文等效支点位置计算式的实用性。计算对象为4根轴组成的轴系，该轴系为实船的缩比尺寸轴系，从艉部往艏部看，依次为尾轴、2根中间轴和一根推力轴，共有6个径向轴承，校中轴系参数和各轴承安装位置如图7和表4所示。在推进轴系校中计算有限元模型中，螺旋桨可简化为刚性质量单元；而轴段的长度与截面直径之比通常较大，可采用梁单元模型模拟；为简便起见忽略轴承油膜和水膜的影响，将轴承简化为线性弹簧单元。有限元法计算的物理参数与三弯矩法相同，两端也设置为自由端，不进行约束，在实支撑区域进行约束，虚支撑处不加任何约束，施加的载荷为简化的集中载荷。

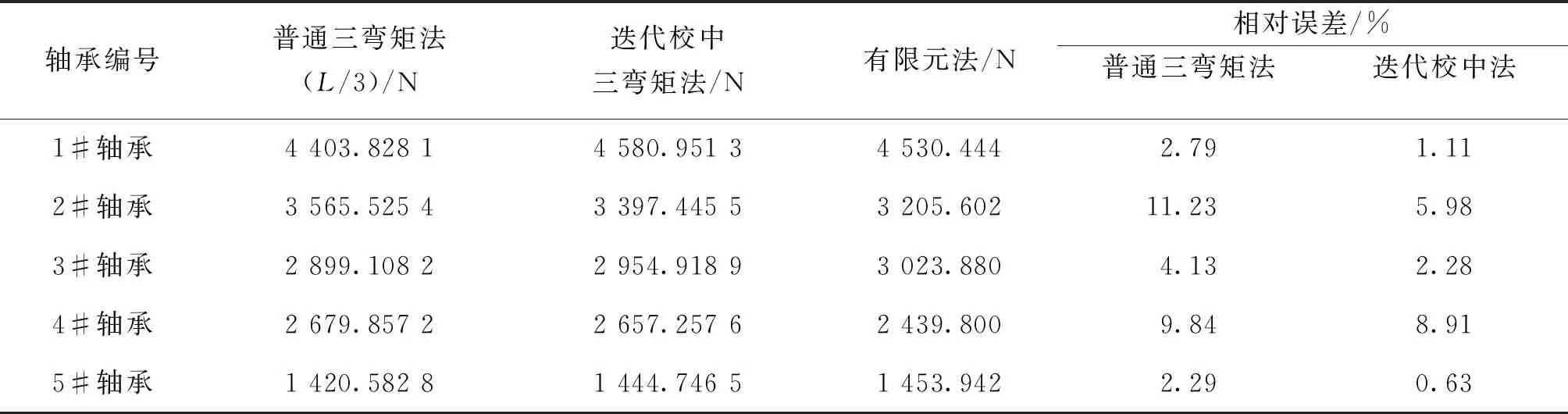
表3 3种方法的支反力计算结果

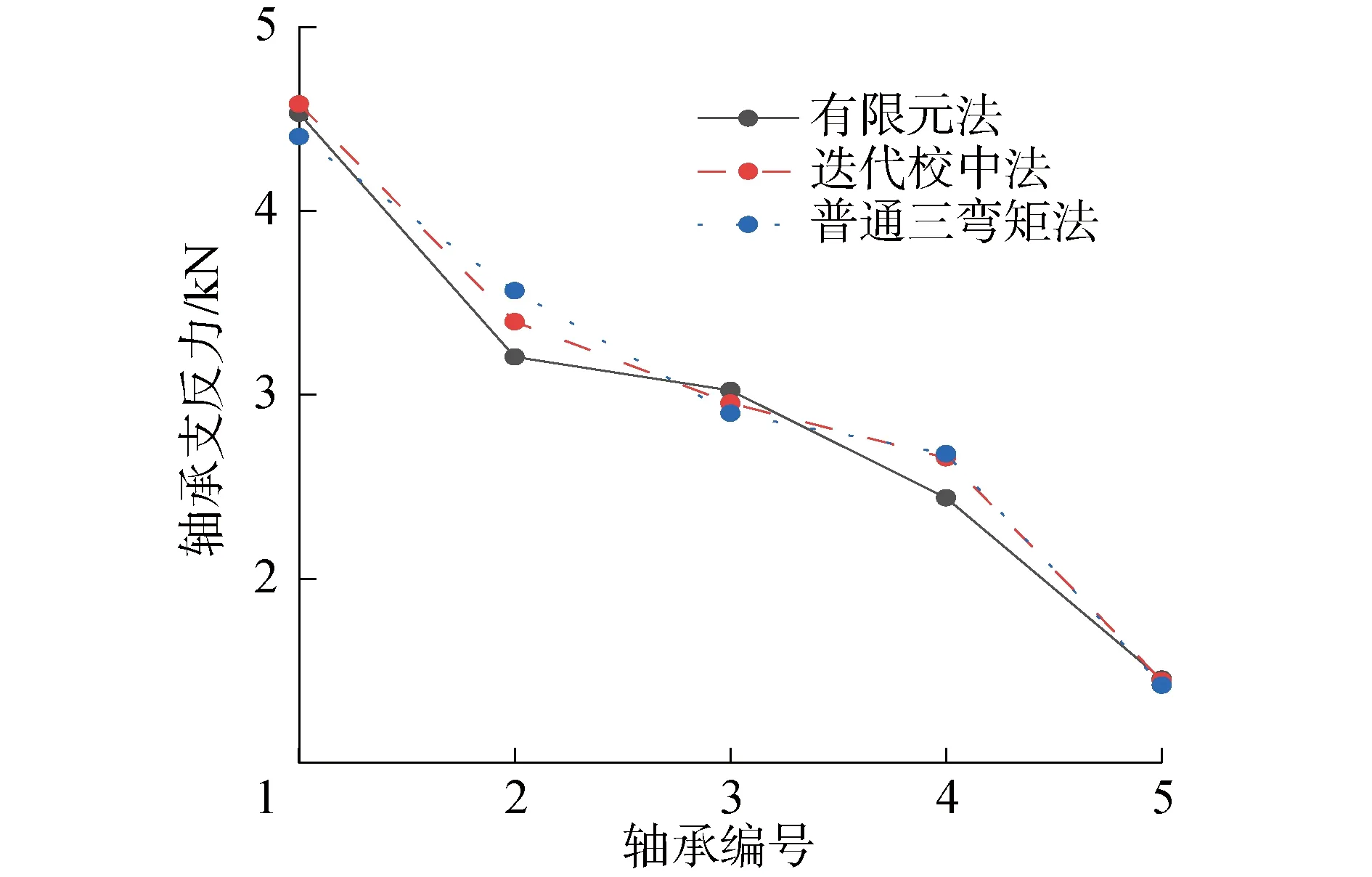
图6 3种方法轴承支反力计算结果

图7 轴系校中三维模型

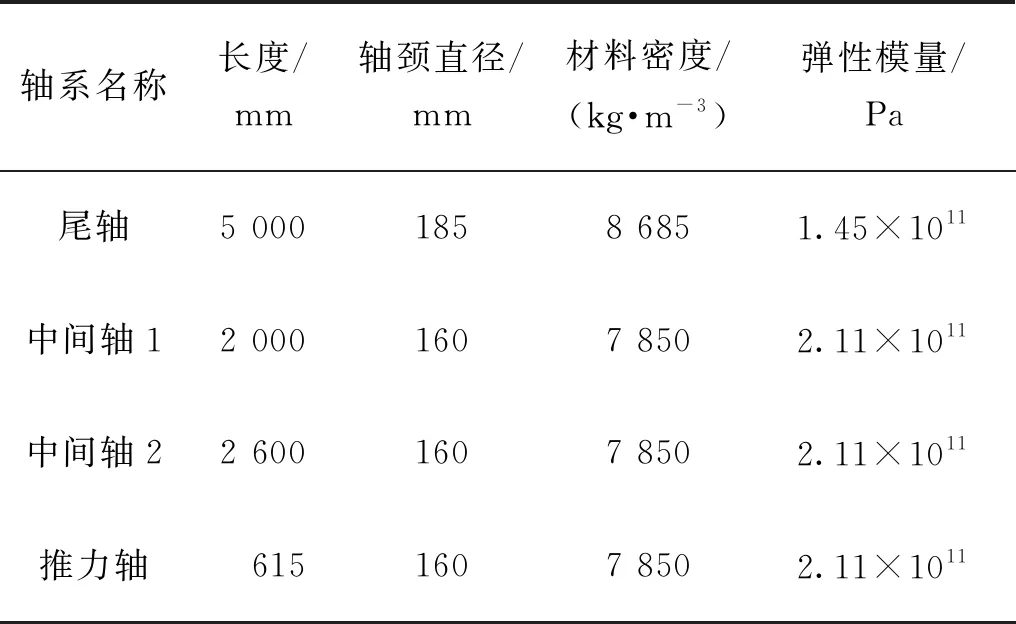
表4 校中轴系参数

将有限元法、普通三弯矩法、迭代校中三弯矩法得到的各轴承支反力结果进行对比，如表3和图6所示。可知，基于迭代三弯矩法的1#后尾轴承支反力计算结果与有限元法非常接近，相比普通三弯矩法，相对误差减小了约60.22%，其余轴承处的支反力计算结果也均比普通三弯矩法更接近于有限元法，证明迭代校中法具有较高的预测精度，也反映了本文提出的轴承等效支点位置计算式具有良好的可用性。轴承等效支点计算式和迭代校中法的建模和仿真计算速度比有限元法快，计算精度优于传统三弯矩法，可以在舰船推进轴系方案设计阶段快速、准确的设计轴承。

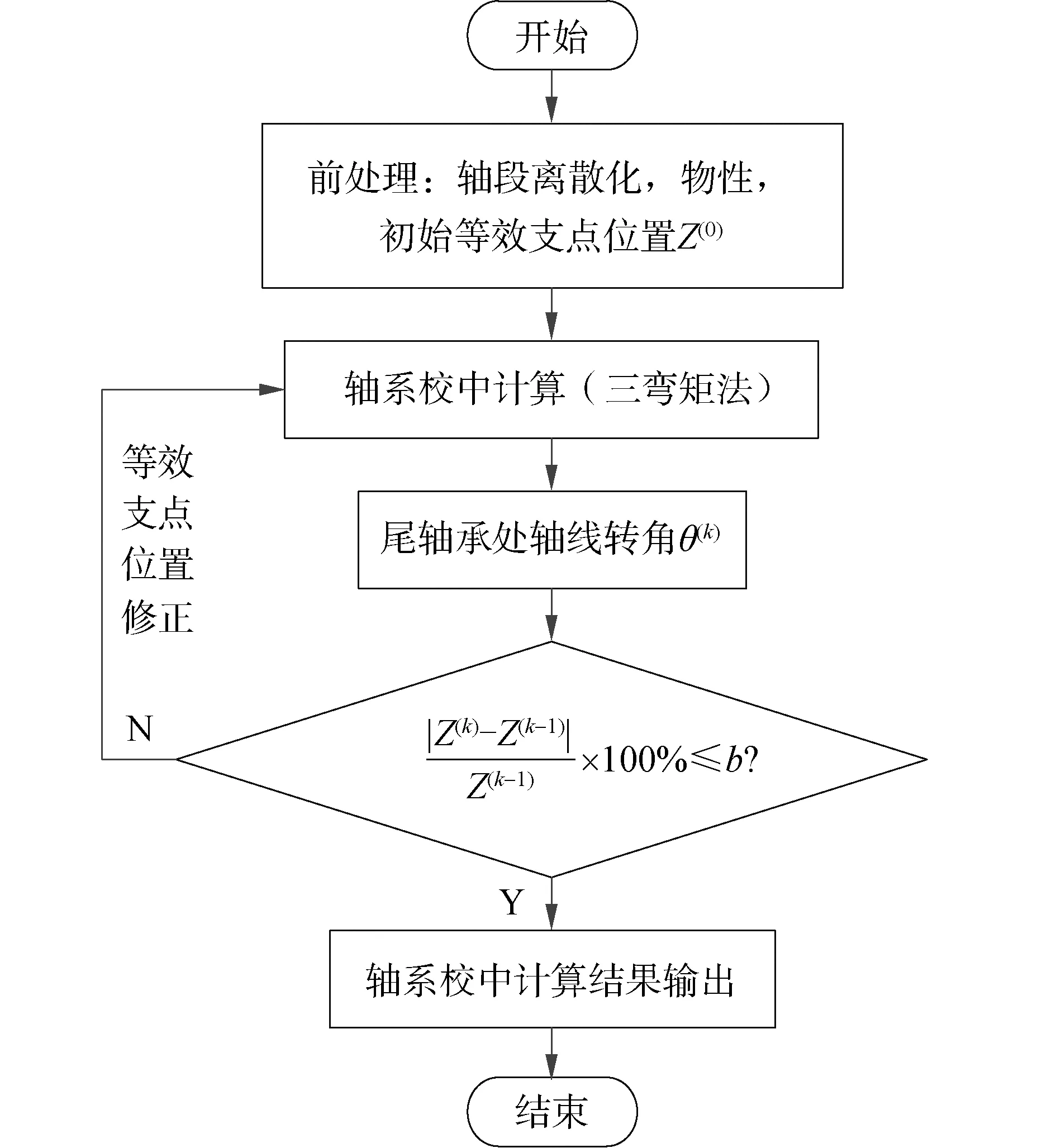
图5 推进轴系校中迭代计算流程

5 结论

1)轴线倾角、尾轴承长径比和内衬弹性模量对尾轴承等效支点位置影响非常显著。当两个因素固定，随着轴线倾角的增大，轴承等效支点位置呈线性减小；长径比越大，轴承接触应变分布越均匀，应变值变化幅度更小，轴承等效支点的位置先增大后减小；尾轴承等效支点位置随内衬弹性模量的增大而减小，弹性模量从7 MPa增大到2 300 MPa，等效支点位置减小。

2)给出了考虑上述三因素的舰船水润滑尾轴承等效支点位置拟合计算式。拟合公式解与原有限元仿真解的平均误差约1%，只有一个算例的误差为6%，表明拟合精度较高。

3)7种新算例的应用验证表明，尾轴承等效支点位置拟合公式解与有限元解的最大相对误差小于4%，表明本文的计算式具有较高的预测精度。

4)提出了融合等效支点位置计算的推进轴系迭代校中算法，算例表明，相比普通三弯矩法，后尾轴承支反力的迭代校中计算结果与有限元结果的相对误差减小了约60.22%，验证了该方法的预测精度，可以在舰船推进轴系方案设计阶段快速、准确的设计轴承支反力。